
Использование программы « GeoGebra »
на уроках математики для
визуализации изучаемого материала

Что же такое GeoGebra?
Это интерактивная свободно распространяемая компьютерная среда. Автором разработчиком которой является Маркус Хохенвартер. GeoGebra позволяет визуализировать математику, проводить эксперименты и исследования при решении математических задач не только геометрического характера. GeoGebra позволяет создавать на экране компьютера чертежи, которые можно использовать на разных стадиях изучения учебного материала, от живых плакатов до исследовательских работ. Особенно поучителен сам процесс создания соответствующего рисунка.
Скачать данную программу можно на сайте: http://www.geogebra.org/cms// .
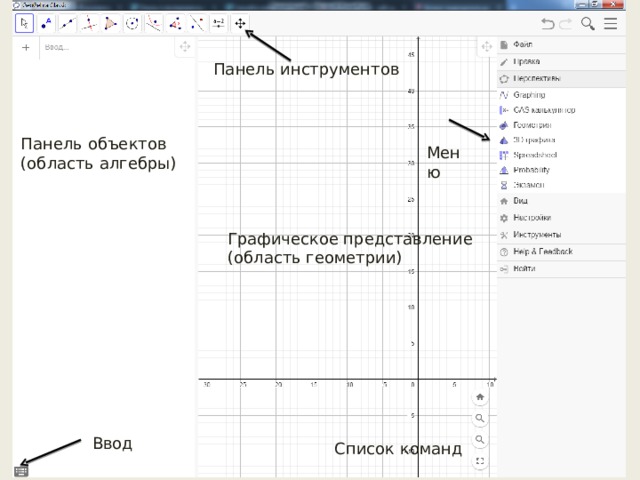
Панель инструментов
Меню
Панель объектов
(область алгебры)
Графическое представление
(область геометрии)
Ввод
Список команд
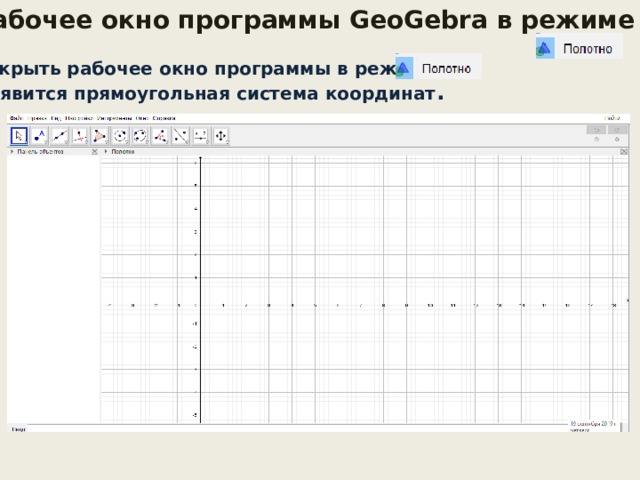
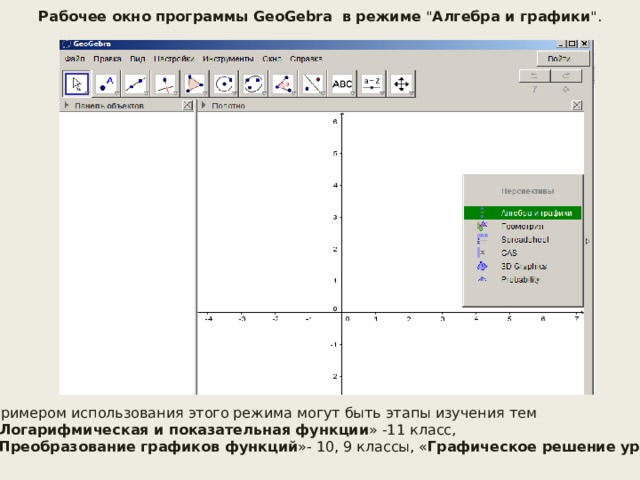
Рабочее окно программы GeoGebra в режиме
- Открыть рабочее окно программы в режиме
- Появится прямоугольная система координат .
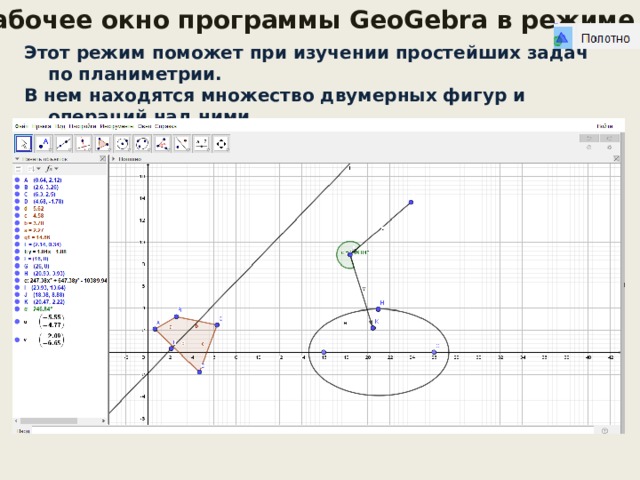
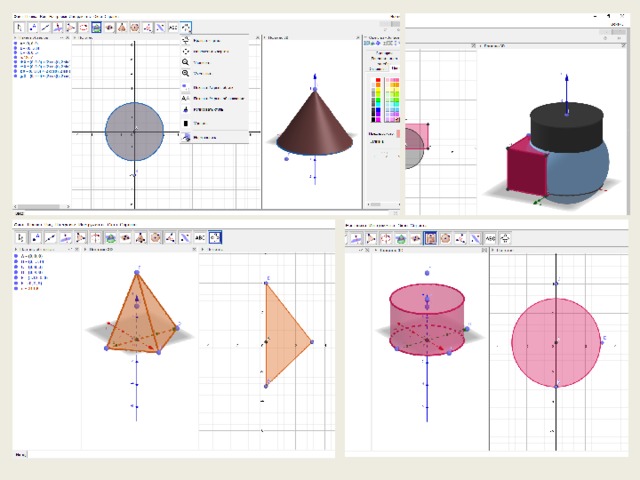
Рабочее окно программы GeoGebra в режиме
Этот режим поможет при изучении простейших задач по планиметрии.
В нем находятся множество двумерных фигур и операций над ними

Рабочее окно программы GeoGebra в режиме
- Открыть рабочее окно программы в режиме
- Появится прямоугольная система координат в пространстве.

Рабочее окно программы GeoGebra в режиме
Примером использования этого режима могут быть этапы изучения темы « Прямоугольный параллелепипед. Куб .» - 5 класс
- Открыть рабочее окно программы в режиме
- Появится прямоугольная система координат в пространстве .
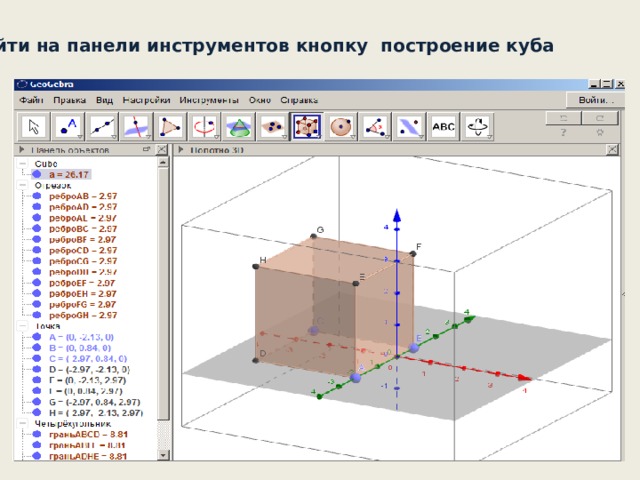
3. Найти на панели инструментов кнопку построение куба
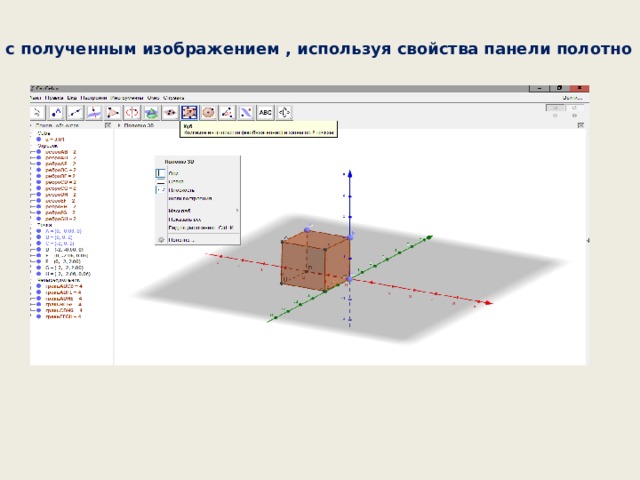
4. Работа с полученным изображением , используя свойства панели полотно 3D :
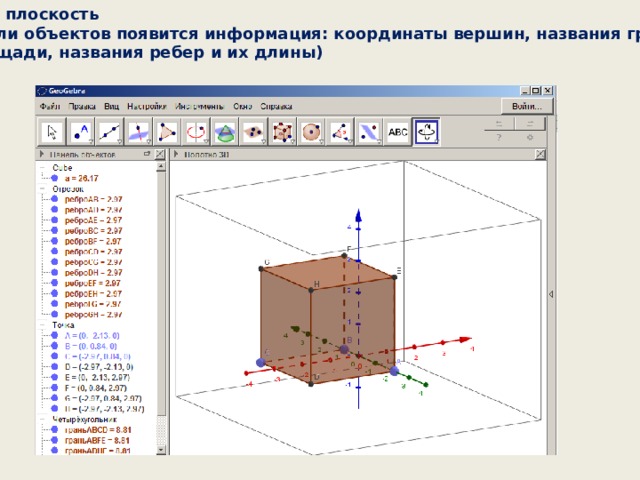
5. Убрать плоскость
(на панели объектов появится информация: координаты вершин, названия граней
и их площади, названия ребер и их длины)
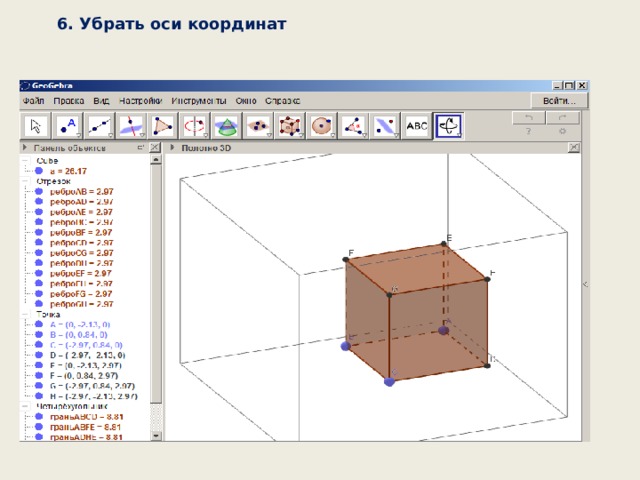
6. Убрать оси координат
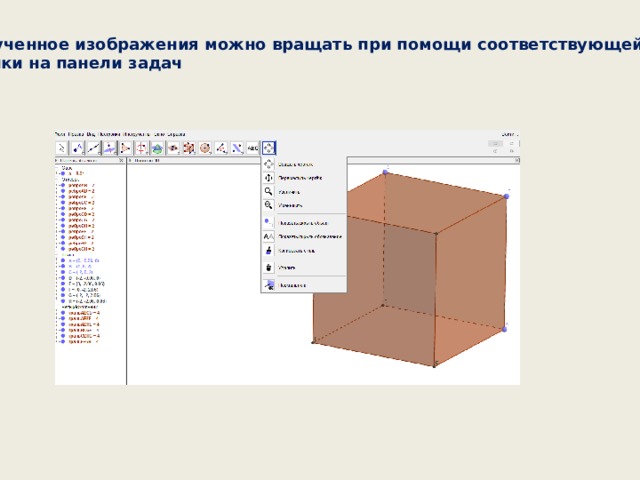
Полученное изображения можно вращать при помощи соответствующей
кнопки на панели задач

Аналогичные действия можно совершить при рассмотрении сферы:
- изображение сферы;
- уравнение сферы;
- сечение сферы плоскостью;
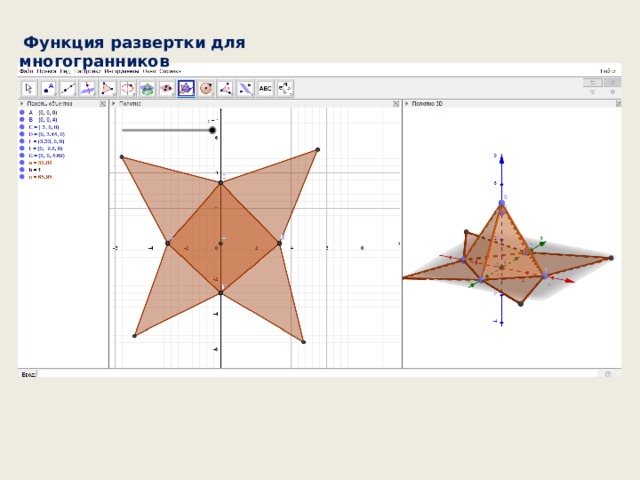
Функция развертки для многогранников
Рабочее окно программы GeoGebra в режиме " Алгебра и графики ".
Примером использования этого режима могут быть этапы изучения тем
« Логарифмическая и показательная функции » -11 класс,
« Преобразование графиков функций »- 10, 9 классы, « Графическое решение уравнений ».
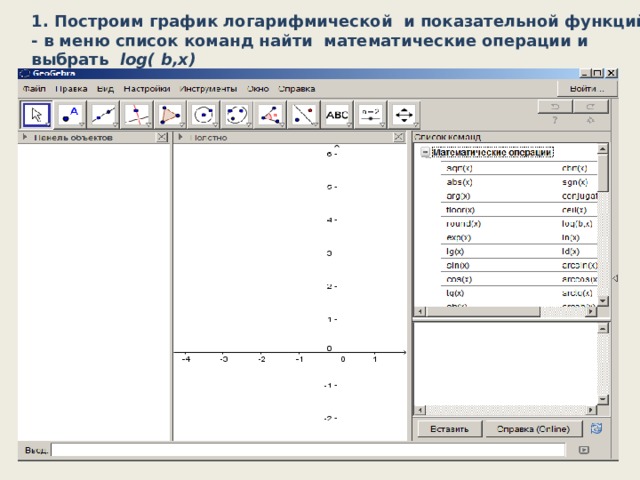
1. Построим график логарифмической и показательной функций:
- в меню список команд найти математические операции и выбрать log ( b , x )
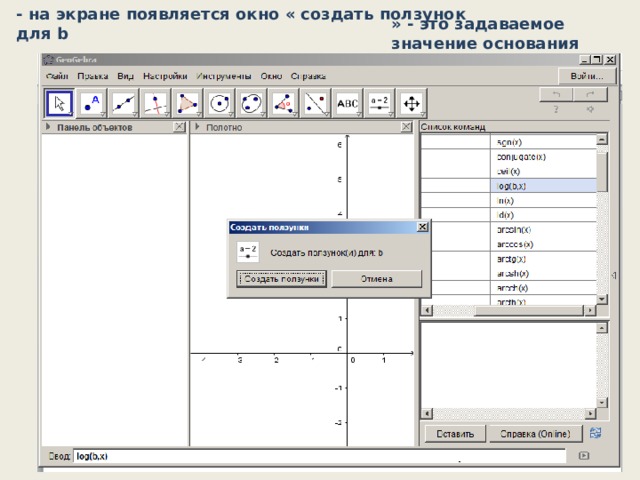
- на экране появляется окно « создать ползунок для b
» - это задаваемое значение основания
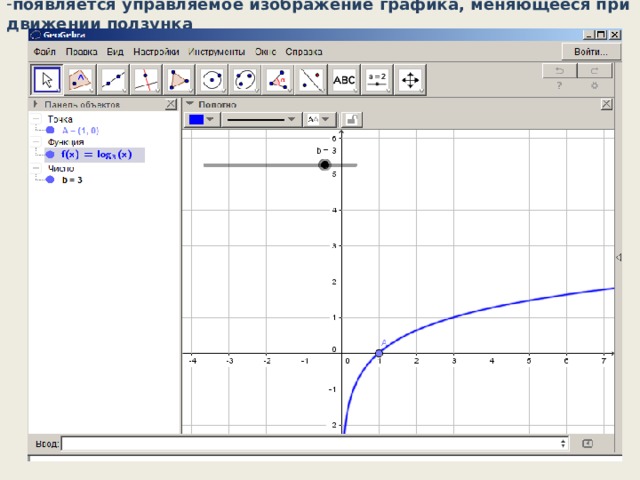
- появляется управляемое изображение графика, меняющееся при движении ползунка
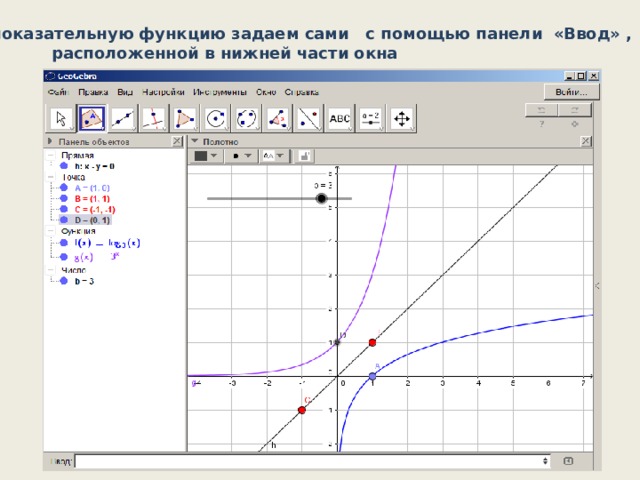
- показательную функцию задаем сами с помощью панели «Ввод» ,
расположенной в нижней части окна
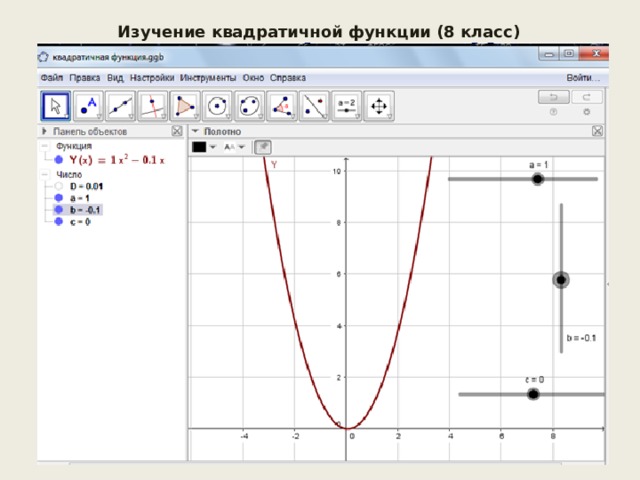
Изучение квадратичной функции (8 класс)
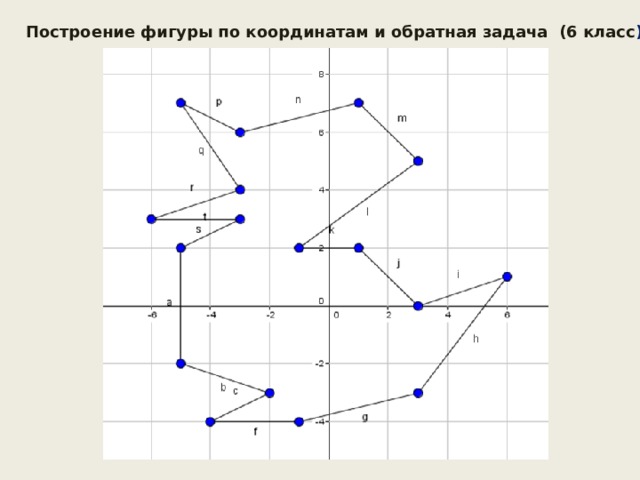
Построение фигуры по координатам и обратная задача (6 класс )
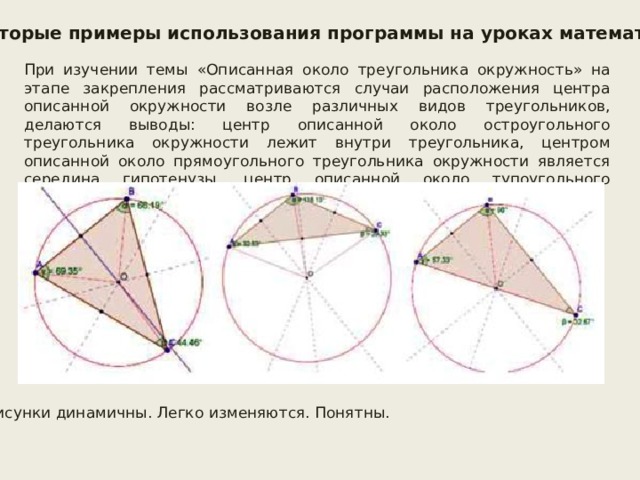
Некоторые примеры использования программы на уроках математики
При изучении темы «Описанная около треугольника окружность» на этапе закрепления рассматриваются случаи расположения центра описанной окружности возле различных видов треугольников, делаются выводы: центр описанной около остроугольного треугольника окружности лежит внутри треугольника, центром описанной около прямоугольного треугольника окружности является середина гипотенузы, центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Рисунки динамичны. Легко изменяются. Понятны.
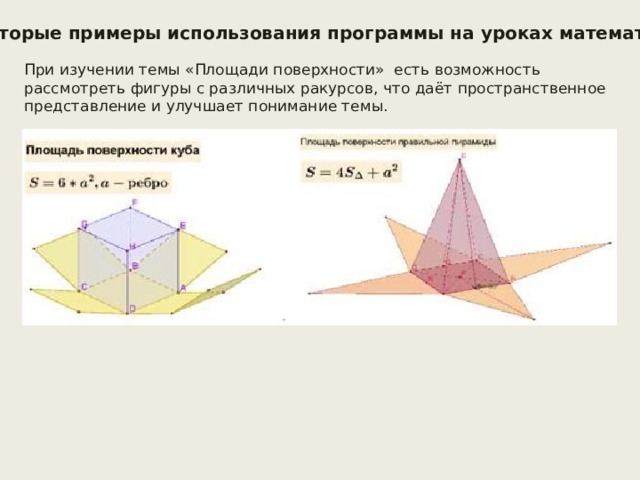
Некоторые примеры использования программы на уроках математики
При изучении темы «Площади поверхности» есть возможность рассмотреть фигуры с различных ракурсов, что даёт пространственное представление и улучшает понимание темы.
 0, a " width="640"
0, a " width="640"
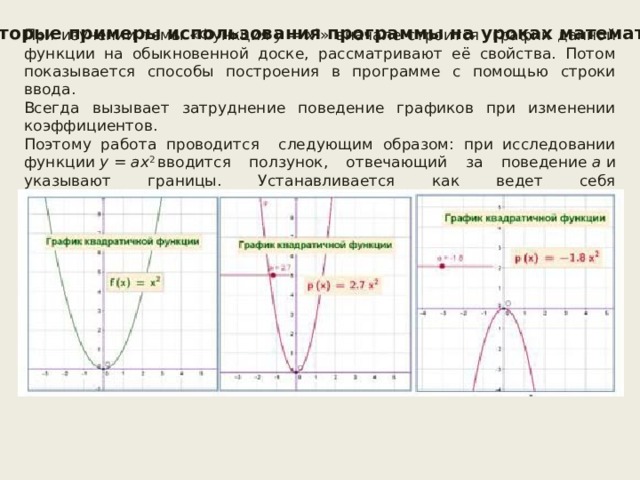
Некоторые примеры использования программы на уроках математики
При изучении темы «Функция y = x 2 » вначале строится график данной функции на обыкновенной доске, рассматривают её свойства. Потом показывается способы построения в программе с помощью строки ввода.
Всегда вызывает затруднение поведение графиков при изменении коэффициентов.
Поэтому работа проводится следующим образом: при исследовании функции y = ax 2 вводится ползунок, отвечающий за поведение a и указывают границы. Устанавливается как ведет себя график y = ax 2 при, a 0, a
Интересны форматы сохранения файлов: .ggb, .html, .png, .ps,.pdf, .gif. А также есть уникальная возможность поделиться своими работами с другими людьми в едином Интернет-пространстве https://www.geogebra.org/galina.mezhonova?p=materials.































 0, a " width="640"
0, a " width="640"






















