Исследовательская работа «Формированию вычислительных навыков на уроках математики в начальных классах.»

Исследовательская работа

«Формированию вычислительных навыков на уроках математики в начальных классах.»

Учителя начальных классов

Филиала МОУ-СОШ с. Комсомольское в с.Кирово

Досмухамбетовой Светланы Валентиновны

СОДЕРЖАНИЕ

ВВЕДЕНИЕ……………………………………………………………....3

1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ У МЛАДШИХ ШКОЛЬНИКОВ ………

1. Понятие «вычислительный навык» и этапы его формирования

2. Психолого-педагогические особенности формирования вычислительных навыков у младших школьников ………………

3. Типы заданий, направленных на формирование вычислительных навыков в начальной школе……………………….

2 Организация практической деятельности по формированию вычислительных навыков у учащихся 2 класса на уроках математики

2.1. Констатирующий этап (выявление исходного уровня сформированности вычислительных навыков у учащихся 2 класса)

2.2. Формирующий этап (работа по формированию вычислительных навыков у учащихся 2 класса)

2.3. Контрольный этап (повторная диагностика и сравнительный анализ результатов относительно первого этапа)

ЗАКЛЮЧЕНИЕ………………………………………………………………..

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ………………………….

ВВЕДЕНИЕ.

Одной из важнейших задач обучения математике младших школьников является формирование у них вычислительных навыков, основу которых составляет осознанное и прочное усвоение приемов устных и письменных вычислений. Вычислительная культура является тем запасом знаний и умений, который находит повсеместное применение, является фундаментом изучения математики и других учебных дисциплин.

В век компьютерной грамотности значимость вычислительных навыков, несомненно, уменьшилась. Использование компьютера, калькулятора во многом облегчает процесс вычислений. Но пользоваться техникой без осознания вычислительных навыков невозможно, да и микрокалькулятор не всегда может оказаться под рукой. Следовательно, владение вычислительными навыками необходимо. Научиться быстро и правильно выполнять вычисления важно для младших школьников как в плане продолжающейся работы с числами, так и в плане практической значимости для дальнейшего обучения. Поэтому вооружение учащихся прочными вычислительными навыками продолжает оставаться серьезной педагогической проблемой.

Проблема формирования у учащихся вычислительных умений и навыков всегда привлекала особое внимание психологов, дидактов, методистов, учителей. В методике математики известны исследования Е.С. Дубинчук, А.А. Столяра, С.С. Минаевой, Н.Л. Стефановой, Я.Ф. Чекмарева, М.А. Бантовой, М.И. Моро, Н.Б. Истоминой, С.Е. Царевой и др.

Глубоко и всесторонне вопросы совершенствования устных и письменных вычислений учащихся исследовались лишь в 60-70 гг. ХХ века. Исследования последующих лет посвящены преимущественно разработке качеств вычислительных навыков (М.А. Бантова), рационализации вычислительных приемов (М.И. Моро, С.В. Степанова и др.), применению средств ТСО (В.И. Кузнецов), дифференциации и индивидуализации процесса формирования вычислительных умений и навыков (Т.И. Фаддейчева).

Каждое из этих исследований внесло определенный вклад в разработку и совершенствование той методической системы, которая использовалась в практике обучения, и нашло отражение в учебниках математики.

Действующие на сегодняшний день программы по математике обеспечивают достаточный уровень формирования вычислительных навыков школьников. Изучение вычислительного приема происходит после того, как школьники усвоят его теоретическую основу (определения арифметических действий, свойства действий и следствия, вытекающие из них). Причем в каждом конкретном случае учащиеся осознают сам факт использования соответствующих теоретических положений, лежащих в основе вычислительного приема, конструируют различные приемы для одного случая вычислений, используя различные теоретические положения. В начальном курсе математики предусмотрен такой порядок введения вычислительных приемов, при котором постепенно вводятся приемы, включающие большее число операций, а приемы, усвоенные ранее, включаются в новые в качестве основных операций.

Переориентация методической системы на приоритет развивающей функции по отношению к образовательной, характеризующейся изменением характера деятельности учащихся, личностно-ориентированным подходом к обучению, несколько ослабила внимание к развитию и закреплению вычислительных навыков у учащихся.

Учебники математики ориентированы на общие вычислительные навыки, и учитель может легко обучить алгоритму вычислений. Но в учебниках, к сожалению, нет «отработки частных способов вычислений», равно как нет и общих способов. 1

Отмечается ухудшение качества вычислений учащихся, обучающихся и по обычным, и по развивающим учебникам. Особенно пострадала культура устного счета. «Стремление учителей изменить ситуацию приводит к тому, что одни учителя используют в работе два учебника: один выполняет развивающие функции, другой (традиционный) — нацелен на формирование вычислительных умений и навыков. Другие учителя увеличивают объем домашних заданий. Это приводит к перегрузкам школьников, провоцирует стрессовые ситуации, снижает интерес к математике». [12, с.5]

Объектом исследования является математическое образование младших школьников.

Предмет исследования – задания, способствующие формированию у младших школьников вычислительных навыков.

Цель исследования – разработать совокупность заданий, способствующих эффективному и осознанному формированию вычислительных навыков.

В соответствии с целью исследования были определены следующие задачи:

1. Изучить и охарактеризовать понятие «вычислительный навык», описать этапы его формирования.

2. Выбрать типы заданий, направленных на формирование вычислительных навыков в начальной школе.

3. Описать логику проведения констатирующего этапа эксперимента по выявлению уровня сформированности вычислительных навыков у учащихся 2 класса.

4. Разработать совокупность заданий, способствующих эффективному и осознанному формированию вычислительных навыков.

В процессе работы были использованы следующие методы исследования:

1. Теоретический: анализ и обобщение.

2. Эмпирический: изучение и анализ психолого-педагогической литературы, учебников и программ по математике, педагогический эксперимент по изучению уровня сформированности вычислительных навыков.

3. Методы математической обработки информации, полученной в ходе эксперимента, и обобщение результатов.

4. Методы презентации: таблицы, диаграммы.

Экспериментальная база: МОУ-СОШ с. Кирово Краснокутского района Саратовской области, 2 класс.

1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ФОРМИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ У МЛАДШИХ ШКОЛЬНИКОВ

1. Понятие «вычислительный навык» и этапы его формирования

Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе.   Эти навыки должны формироваться осознанно и прочно, так как на их базе строится весь начальный курс обучения математике, который предусматривает формирование вычислительных навыков на основе сознательного использования приемов вычислений. Последнее становится возможным благодаря тому, что в программу включено знакомство с некоторыми важнейшими свойствами арифметических действий и вытекающими из них следствиями.

М.А. Бантова определила вычислительный навык как высокую степень овладения вычислительными приемами. «Приобрести вычислительные навыки — значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия, и выполнять эти операции достаточно быстро». [5, с.39]

Вычислительные навыки рассматриваются как один из видов учебных навыков, функционирующих и формирующихся в процессе обучения. Они входят в структуру учебно-познавательной деятельности и существуют в учебных действиях, которые выполняются посредством определенной системы операций. Полноценный вычислительный навык обучающихся характеризуется следующими показателями: правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом и прочностью. [5]

Правильность – ученик правильно находит результат арифметического действия над данными числами, т.е. правильно выбирает и выполняет операции, составляющие прием.

Осознанность – ученик осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения. Это для ученика своего рода доказательство правильности выбора системы операции. Осознанность проявляется в том, что ученик в любой момент может объяснить, как он решал пример и почему можно так решать. Это, конечно, не значит, что ученик всегда должен объяснять решение каждого примера. В процессе овладения навыком объяснение должно постепенно свертываться.

Рациональность – ученик, сообразуясь с конкретными условиями, выбирает для данного случая более рациональный прием, т. е. выбирает те из возможных операций, выполнение которых легче других и быстрее приводит к результату арифметического действия. Разумеется, что это качество навыка может проявляться тогда, когда для данного случая существуют различные приемы нахождения результата, и ученик, используя различные знания, может сконструировать несколько приемов и выбрать более рациональный. Как видим, рациональность непосредственно связана с осознанностью навыка.

Обобщенность – ученик может применить прием вычисления к большему числу случаев, т. е. он способен перенести прием вычисления на новые случаи. Обобщенность так же, как и рациональность, теснейшим образом связана с осознанностью вычислительного навыка, поскольку общим для различных случаев вычисления будет прием, основа которого - одни и те же теоретические положения.

Автоматизм (свернутость) – ученик выделяет и выполняет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операции. Осознанность и автоматизм вычислительных навыков не являются противоречивыми качествами. Они всегда выступают в единстве: при свернутом выполнении операции осознанность сохраняется, но обоснование выбора системы операции происходит свернуто в плане внутренней речи. Благодаря этому ученик может в любой момент дать развернутое обоснование выбора системы операции. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям (5+3, 8-5,9+6, 15-9, 7-6, 42:6). Здесь должен быть достигнут уровень, характеризующийся тем, что ученик сразу же соотносит с двумя данными числами третье число, которое является результатом арифметического действия, не выполняя отдельных операций. По отношению к другим случаям арифметических действий происходит частичная автоматизация вычислительных навыков: ученик предельно быстро выделяет и выполняет систему операций, не объясняя, почему выбрал эти операции и как выполнял каждую из них.

Прочность – ученик сохраняет сформированные вычислительные навыки на длительное время.

Формирование вычислительных навыков, обладающих названными качествами, обеспечивается построением курса математики и использованием соответствующих методических приемов. 5

Вместе с тем, ученик при выполнении вычислительного приёма должен отдавать отчёт в правильности и целесообразности каждого выполненного действия, то есть постоянно контролировать себя, соотнося выполняемые операции с образцом - системой операций. О сформированности любого умственного действия можно говорить лишь тогда, когда ученик сам, без вмешательства со стороны, выполняет все операции приводящие к решению. Умение осознано контролировать выполняемые операции позволяет формировать вычислительные навыки более высокого уровня, чем без наличия этого умения.

В целях формирования осознанных, обобщенных и рациональных навыков начальный курс математики строится так, что изучение вычислительного приема происходит после того, как учащиеся усвоят материал, являющийся теоретической основой этого вычислительного приема. Например, сначала ученики усваивают свойство умножения суммы на число, а затем это свойство становится теоретической основой приема внетабличного умножения. Так, при умножении 15 на 6 выполняется следующая система операций, составляющая вычислительный прием:

1) число 15 заменяем суммой разрядных слагаемых 10 и 5;

2) умножаем на 6 слагаемое 10, получится 60;

3) умножаем на 6 слагаемое 5, получится 30;

4) складываем полученные произведения 60 и 30, получится 90.

Как видим, здесь применение свойства умножения суммы на число (термин «распределительный закон» в начальном курсе не вводится) определило выбор всех операций, поэтому и говорят, что прием внетабличного умножения основан на свойстве умножения суммы на число или что свойство умножения суммы на число — теоретическая основа приема внетабличного умножения.
Легко заметить, что кроме свойства умножения суммы на число здесь использованы и другие знания, а также ранее сформированные вычислительные навыки: знание десятичного состава чисел (замена числа суммой разрядных слагаемых), навыки табличного умножения и умножения числа 10 на однозначные числа, навыки сложения двузначных чисел. Однако выбор именно этих знаний и навыков диктуется применением свойства умножения суммы на число. Общеизвестно, что теоретической основой вычислительных приемов служат определения арифметических действий, свойства действий и следствия, вытекающие из них. Имея это в виду и принимая во внимание методический аспект, можно выделить группы приемов в соответствии с их общей теоретической основой, предусмотренной действующей программой по математике для начальных классов, что даст возможность использовать общие подходы в методике формирования соответствующих навыков.

Назовем эти группы приемов:
1.       Приемы, теоретическая основа которых — конкретный смысл арифметических действий. К ним относятся: приемы сложения и вычитания чисел в пределах 10 для случаев вида а + 2, а + 3, а + 4, а + 0; приемы табличного сложения и вычитания с переходом через десяток в пределах 20; прием нахождения табличных результатов умножения, прием нахождения табличных результатов деления (только на начальной стадии) и деления с остатком, прием умножения единицы и нуля. Это первые приемы вычислений, которые вводятся сразу после ознакомления учащихся с конкретным смыслом арифметических действий. Они, собственно, и дают возможность усвоить конкретный смысл арифметических действий, поскольку требуют применения конкретного смысла. Вместе с тем эти первые приемы готовят учащихся к усвоению свойств арифметических действий.
Таким образом, хотя в основе некоторых из названных приемов и лежат свойства арифметических действий (так, прибавление двух по единице выполняется на основе использования свойства прибавления суммы к числу), эти свойства учащимся явно не раскрываются. Названные приемы вводятся на основе выполнения операций над множествами.

2.       Приемы, теоретической основой которых служат свойства арифметических действий. К этой группе относится большинство вычислительных приемов. Это приемы сложения и вычитания для случаев вида 53 ± 20, 47 ± 3, 30 – 6, 9 + 3, 12 – 3, 35 ± 7, 40 ± 23, 57 ± 32, 64 ± 18; аналогичные приемы для случаев сложения и вычитания чисел больших, чем 100, а также приемы письменного сложения и вычитания; приемы умножения и деления для случаев вида 14  5, 5  14, 81 : 3, 18  40, 180 : 20, аналогичные приемы умножения и деления для чисел больших 100 и приемы письменного умножения и деления. Общая схема введения этих приемов одинакова: сначала изучаются соответствующие свойства, а затем на их основе вводятся приемы вычислений.

3.       Приемы, теоретическая основа которых — связи  между  компонентами  и  результатами  арифметических действий. К ним относятся приемы для случаев вида 9  7, 21 : 3, 60 : 20, 54 : 18, 9 : 1, 0 : 6. При введении этих приемов сначала рассматриваются связи между компонентами и результатом соответствующего арифметического действия, затем на этой основе вводится вычислительный прием.

4.       Приемы, теоретическая основа которых  —  изменение результатов арифметических действий в зависимости от изменения одного из компонентов. Это приемы округления при выполнении сложения и вычитания чисел (46 + 19, 512 – 298) и приемы умножения и деления на 5, 25, 50. Введение этих приемов также требует предварительного изучения соответствующих зависимостей.
5.       Приемы, теоретическая основа которых — вопросы нумерации чисел. Это приемы для случаев вида а ± 1, 10 + 6, 16 – 10, 16 – 6, 57  10, 1200 : 100; аналогичные приемы для больших чисел. Введение этих приемов предусматривается после изучения соответствующих вопросов нумерации (натуральной последовательности, десятичного состава чисел, позиционного принципа записи чисел).

6.       Приемы, теоретическая основа которых — правила. К ним относятся приемы для двух случаев: а  1, а  0. Поскольку правила умножения чисел на единицу и нуль есть следствия из определения действия умножения целых неотрицательных чисел, то они просто сообщаются учащимся и в соответствии с ними выполняются вычисления.

Целый ряд случаев может быть отнесен не только к указанной группе приемов, но и к другой. Например, случаи вида 46 + 19 можно отнести не только к четвертой группе, но и ко второй. Это зависит от выбора теоретической основы вычислительного приема. Как видим, все вычислительные приемы строятся на той или иной теоретической основе, причем в каждом случае учащиеся осознают сам факт использования соответствующих теоретических положений, лежащих в основе вычислительных приемов. Это — реальная предпосылка овладения учащимися осознанными вычислительными навыками. Общность подходов к раскрытию вычислительных приемов каждой группы — есть залог овладения учащимися обобщенными вычислительными навыками. Возможность использования различных теоретических положений при конструировании различных приемов для одного случая вычисления (например, для случая сложения 46 + 19) является предпосылкой формирования рациональных гибких вычислительных навыков.

В ходе формирования вычислительных навыков М.А. Бантова выделяет следующие этапы:

1. Подготовка к введению нового приёма.

На этом этапе создается готовность к усвоению вычислительного приёма, а именно, учащиеся должны усвоить те теоретические положения, на которых основывается приём вычислений, а также овладеть каждой операцией, составляющей приём.
Например, можно считать, что ученики подготовлены к восприятию вычислительного приёма ±2, если они ознакомлены с конкретным смыслом действий сложения и вычитания, знают состав числа 2 и овладели вычислительными навыками сложения и вычитания вида ±1; готовностью к введению приёма внетабличного умножения (13  6) будет знание учащимся правила умножения суммы на число, знание десятичного состава чисел в пределах 100 и овладение навыками табличного умножения, навыками умноженная числа 10 на однозначные числа, навыками сложения двузначных чисел.
Центральное звено при подготовке к введению нового приёма - овладение учеником основными операциями.

2. Ознакомление с вычислительным приёмом.

На этом этапе ученики усваивают суть приёма: какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия.
При введении большинства вычислительных приёмов важно использовать наглядность. В некоторых случаях это оперирование множествами. Например, прибавляя к 6 число 3, придвигаем к 6 квадратам 3 квадрата по одному. В других случаях в качестве наглядности используется развернутая запись. Например, при введении приёма внетабличного умножения выполняется запись:

13  6=(10 + 3)  6=10  6 + 3  6 = 60 + 18 = 78

Выполнение каждой операции важно сопровождать пояснениями вслух.
Сначала эти пояснения выполняется под руководством учителя, а потом самостоятельно учащимися.

3. Закрепление знаний приёма и выработка вычислительного навыка.

На этом этапе ученики должны твердо усвоить систему операций, составляющие приём, и быстро выполнить эти операции; то есть овладеть вычислительным навыком.
В процессе работы здесь важно предусмотреть этапы в становлении у учащихся вычислительных навыков:

1. На первом этапе закрепляется знание приема: учащиеся самостоятельно выполняют все операции, составляющие прием, комментируя выполнение каждой из них вслух и одновременно производя развернутую запись 34  5 = (30 + 4)  5 = 30  5 + 4  5 = 3  10  5 + 20 = 3  5  10 + 20 = 15  10 + 20 = 150 + 20 = (100 + 50) + 20 = 100 + (50 + 20) = 100 + 70 = 170

2. На втором этапе происходит частичное свертывание выполнения операций: учащиеся про себя выделяют операции и обосновывают выбор, порядок их выполнения, вслух же они проговаривают выполнение основных операций, т.е. промежуточных вычислений. Надо учить детей выделять основные операции в каждом вычислительном приёме. Развёрнутая запись не выполняется. Сначала проговаривание ведётся под руководством учителя, а затем самостоятельно. Проговаривание вслух помогает выделить основные операции, а выполнение про себя вспомогательных операций способствует их свёртыванию.

34  5 = (30 + 4)  5 = 30  5 + 4  5 = 150 + 20 = 170

1. На третьем этапе происходит полное свертывание выполнения операций: учащиеся про себя выделяют и выполняют все операции, т.е. здесь происходит свёртывание и основных операций. Учитель предлагает детям выполнять про себя и промежуточные вычисления, а называть или записывать только окончательный результат. 34  5 = 170

2. На четвёртом этапе наступает предельное свёртывание выполнения операций. Учащиеся выполняют все операции в свёрнутом плане, предельно быстро, т.е. они овладевают вычислительными навыками. Это достигается в результате выполнения достаточного числа тренировочных упражнений.

На всех этапах формирования вычислительного навыка решающую роль играют задания на применение вычислительных приёмов, причём содержание заданий должно подчиняться целям, которые ставятся на соответствующем этапе. Важно, чтобы было достаточное число заданий, чтобы они были разнообразными как по форме, так и по числовым данным. Надо иметь в виду, что свёртывание выполнение операций не у всех учащихся происходит одновременно, поэтому важно время от времени возвращаться к полному объяснению и развёрнутой записи приёма. Продолжительность каждого этапа определяется сложностью приёма, подготовленностью учащихся и целями, которые ставятся на каждом этапе. Правильное выделение этапов позволит учителю управлять процессом усвоения учащимися вычислительного приёма, постепенного свёртывания выполнения операций, образования вычислительных навыков.

В системе Л. В. Занкова формирование навыков проходит три принципиально различных этапа, при этом учитель может использовать два пути: прямой и косвенный.

Прямой путь в чистом виде предполагает сообщение учащимся образца, алгоритма выполнения операции, на основании которого школьники многократно ее выполняют. В результате такой репродуктивной деятельности достигается запоминание предложенного алгоритма и вырабатывается запланированный навык.
Косвенный путь предполагает, прежде всего, включение учеников в продуктивную творческую деятельность, в самостоятельной поиск алгоритма выполнения операции.
В системе общего развития Л.В. Занкова главным является именно косвенный путь формирования вычислительных навыков, прямой же использует учитель тогда и в той мере, как это необходимо, так как в чистом виде ни один из путей использовать нельзя. 15

Первый этап – осознание основных положений, лежащих в фундаменте выполнения операции, создание алгоритма ее выполнения. На этом обязательно прослеживается, оценивается и создается каждый шаг в рассуждениях детей, устные рассуждения переводятся в запись математическими знаками. Отсюда вытекает характерный признак этого этапа - подробная запись выполнения операции, с которой в данный момент работают ученики. На этом этапе практически не используется прямой путь. Он возникает только при выполнении промежуточных, знакомых детям операций. Результатом этого этапа является выработка алгоритма выполнения операции и его осознание.

284  25 = 284  (20 + 5) = 284  20 + 284  5 = 284  (2  10) + 1420 = (284  2)  10 + 1420 = 568  10 + 1420 = 5680 + 1420 = 7100.

На этом этапе почти не используем прямой путь, если только при выполнении знакомых детям операций, т.е. промежуточных (умножение на однозначное число, на единицу с нулями и выполнение сложения).
В результате деятельности на этом этапе появляется алгоритм выполнения операции.

Главным направлением второго этапа является формирование правильного выполнения операции. Для достижения этой цели необходимо не только использование выработанного на первом этапе алгоритма выполнения операции, но, может быть, в еще большей степени, свободная ориентация в ее нюансах, умение предвидеть. К чему приведет то или иное изменение компонентов операции. В силу этого на втором этапе используются оба пути формирования навыков, однако косвенный путь продолжает быть ведущим, прямой же используется в качестве подчиненного. Ученикам даются такие задания, которые ставят детей в позицию активного творческого поиска, где они используют свои знания в нестандартном преобразованном виде.
Например, даем задание: изменить в произведении 284  25 одну цифру так, чтобы значение произведения стало пятизначным числом.
В результате найденных преобразований каждый ученик получает от 6 – до 12 произведений, изменяя цифру во втором или в первом множителе:
284  35, 284  45, 284  55, 284  65, 284  75 (85, 95, 55)
384  25, 484  25 (584, 684, 784, 884,984)  25.

От учащихся не требуется нахождения и составления всех возможных решений. Мы объединяем все случаи, которые нашли разные ученики, анализируем, находим с ними определенную закономерность, отыскиваем пропущенные варианты.
Важная особенность таких заданий – возможность индивидуализации их выполнения каждым учеником, так как нет жестких установок на количество требуемых решений, а только рекомендации: «Постарайся найти не одно решение».
Третий этап формирования навыка нацелен на достижение высокого темпа выполнения операции. Именно на этом этапе на первый план выходит прямой путь формирования навыка. Главная задача учителя – построить работу так, чтобы дети хотели выполнять необходимые вычисления и получали от этого удовольствие.

Формирование вычислительных умений и навыков - это сложный длительный процесс, его эффективность зависит от индивидуальных особенностей ребенка, уровня его подготовки и организации вычислительной деятельности.

На современном этапе развития образования необходимо выбирать такие способы организации вычислительной деятельности школьников, которые способствуют не только формированию прочных вычислительных умений и навыков, но и всестороннему развитию личности ребенка.

При выборе способов организации вычислительной деятельности необходимо ориентироваться на развивающий характер работы, отдавать предпочтение обучающим заданиям. Используемые вычислительные задания должны характеризоваться вариативностью формулировок, неоднозначностью решений, выявлением разнообразных закономерностей и зависимостей, использованием различных моделей (предметных, графических, символических), что позволяет учитывать индивидуальные особенности ребенка, его жизненный опыт, предметно-действенное и наглядно-образное мышление и постепенно водить ребенка в мир математических понятий, терминов и символов.

1. Психолого-педагогические особенности формирования вычислительных навыков у младших школьников

Характерной особенностью ребенка в первые годы пребывания в школе является то, что он, так же, как и дошкольник, воспринимает цель взрослых как свою личную. Но постепенно у детей младшего школьного возраста развивается произвольность психических процессов, у них формируется умение сознательно ставить собственную цель действий и находить способы для их достижения.

В младшем школьном возрасте у детей быстро развиваются такие важные для всего дальнейшего обучения психические явления, как рефлексия, это умение объективно анализировать собственные действия и поступки с точки зрения их соответствующей цели и условиям деятельности, внутренний план действий- умение планировать и совершать в уме, про себя, разные операции соответственно поставленной задаче. Одновременно у детей быстро развиваются познавательные способности, а также произвольное внимание, память, воображение.

Развитие всех этих способностей и умений, играющих решающую роль в становлении личности учащихся, в формировании их познавательных возможностей, не происходит автоматически. Необходима настойчивая, кропотливая и целеустремленная работа по формированию и развитию у всех детей этих важных качеств.

Процесс обучения представляет собой сложную динамическую систему, в которой в органичном единстве происходит взаимосвязанная деятельность учителя и ученика.

В этой системе под руководством учителя учащиеся овладевают основами наук, способами деятельности и рациональными приемами работы. Задача учителя состоит не только в том, чтобы сообщать знания, а и управлять процессом усвоения знаний и способов деятельности. Задача ученика- овладевать системой знаний, способами их приобретения, переработки, сохранения и применения, воспитывая в себе необходимые качества личности.

За основную структурную единицу процесса мышления принимается действие. Действие- это единица анализа деятельности учащегося. Учитель должен уметь не только выделять действия, которые входят в разные виды познавательной деятельности учащихся, но и найти их структуру, функциональные части, основные свойства и закономерности их становления.

Действие, которое выполняется человеком, всегда направлено на какой-то предмет. Предметом действия могут быть и слова, и явления, и понятия. Действие всегда целенаправленно. В результате выполнения действия всегда получаем какой-то результат. Цель действия связана с мотивом. Мотив является важным компонентом действия, он неразрывно связан с целью. Мотив побуждает человека ставить и достигать разные цели, выполнять соответствующие действия. Ученик каждый день выполняет много учебных действий. Но не всегда он видит необходимость выполнения этих действий. Поэтому часто учебная деятельность для такого ученика становится тяжелой, он не видит в ней никакого смысла.

В структуру любого действия входит та или другая система операций, с помощью которых действие и выполняется. Очень важным компонентом действия является ориентированная основа. Каждое выполняемое действие, будет проходить успешно, если будут учитываться условия, которые определяют успех этого действия. Учителю необходимо учить детей выделять и осознавать систему условий, на которую необходимо ориентироваться при решении данного задания.

Действие - это целостная система взаимосвязанных между собой элементов. В ходе выполнения действия эти элементы обеспечивают три основные функции: ориентированную, исполнительную, контрольно-корректирующую. Центральной является ориентированная часть действия. Эта часть обеспечивает успех действия. Ученики часто пропускают эту часть, спешат к исполнительной части, то есть к преобразованию предмета действия, к получению результата. Контролирующая часть направлена на проверку результатов первых двух частей, на отслеживание путей выполнения, проверку соответствия его определенному плану.

Психологи А.Н.Леонтьев и П.Д.Гальперин показали, что от характера усвоения знаний, зависит результат ученика. Опираясь на это, разработана теория поэтапного формирования умственных действий. В основе этой теории лежит поэтапный переход от внешнего к осознанному (внутреннему) психическому действию.

Основные положения этой теории такие:

-психическая деятельность является результатом перенесения внешних материальных действий в план отображения- в план восприятия представлений и понятий;

-процесс такого переноса проходит через ряд этапов, на каждом из которых новые отображения и репродукция действия и ее систематическое совершенствование.

Процесс обучения представляет собой управление психической деятельностью ученика на основе обучения умственным действиям и познавательным структурам. Для того, чтобы любые знания и умения формировались полноценно, П.Я.Гальперин предложил такую последовательность этапов:

1. Создание мотивации, как внутренней (интерес к самому процессу деятельности) так и внешней.

2. Объяснение или выделение схемы ориентированной основы действия- выяснение последовательности ориентированных, исполнительных и контрольно-корректирующих операций, которые входят в состав действия.

3. Формирование действия в материальной или в материализированной форме.

Более эффективным является обучение, которое начинается с формирования материализированной формы, тогда обучение направлено на теоретические знания. После формирования материализированной формы действия необходимо переходить к этапу материального действия, то есть к анализу реальных предметов. На третьем этапе вводится речь, ученики комментируют выполненное действие.

1. Формирование действия вслух, без опоры на материально-материализированные способы. Все операции, составляющие действие, должны быть усвоены в речевой форме. Сначала действие проговаривается «своими словами», потом постепенно переходят к научной речи, которая выступает конечным результатом этого этапа.

2. Формирование действия во внутренней речи («про себя»), является переходной ступенью для перевода действия в умственный план. На этом этапе действие начинает сокращаться и автоматизироваться.

3. Переход действия во внутреннюю речь, а оттуда в чистую мысль. На этом этапе действие сдерживает способность к автоматическому протеканию и становится недосягаемой для самонаблюдения. Сознательность контролирует только результат этого процесса.

Рассмотрим формирование вычислительного приема 56-24 на основе применения теории поэтапного формирования умственных действий.

1. Создается проблемная ситуация при решении задачи.

У мальчика было 56 р., 24 р. он потратил. Сколько рублей осталось у мальчика?

Решая с учащимися такую задачу, приходим к выводу, что вычитание вида 56-24, еще не умеем выполнять.

1. Учитель знает, что вычислительный прием этого вида состоит из таких операций:

А) состав двузначного числа;

Б) вычитание однозначных чисел;

В) вычитание круглых десятков;

Г) сложение вида 30+2

Эти операции и являются составляющими алгоритма вычитания двузначных чисел.

На данном этапе отрабатываются уже известные операции с помощью решения устных упражнений.

1. Используя палочки или ленты бумаги с кружочками, каждый ученик выполняет практическую работу под руководством учителя.

-Положите на парту 56 палочек. Сколько в этом числе десятков? Единиц?

-Необходимо отнять 24 палочки. Сколько десятков, единиц необходимо забрать? Сколько палочек осталось? Какое это число?

То есть каждый ученик, практически выполнил все операции алгоритма, наглядно увидел правило: десятки отнимаются от десятков, единицы от единиц.

1. Учитель сообщает образец рассуждения при вычислении: 56- это 50 и 6, 24- это 20 и 4. Десятки отнимаются от десятков, единицы от единиц. 50 -20 будет 30, 6-4 будет 2, 30 и 2 будет 32. На этом этапе учащиеся вслух проговаривают все этапы алгоритма, желательно выполнить это хором.

2. Начинается частичное сворачивание операции. Второстепенными операциями тут будут: 56 это50 и6, 24 это 20 и 4, поэтому вслух проговаривают только основные операции. Рассуждения ученика такие:

-Десятки отнимают от десятков, единицы от единиц.50-20 будет 30, 6-4 будет 2. 30 и 2 будет 32.

6. Происходит полное сворачивание операции и вслух проговаривается результат 56-24=32.

По теории поэтапного формирования умственных действий усвоение знаний рассматривается вместе с усвоением деятельности. Знания с самого начала включаются в структуру действия. Качество знаний при этом объясняется их соответствием деятельности, которая используется для их усвоения. Знания никогда нельзя давать в готовом виде, они всегда усваиваются через включение их в определенную деятельность. При создании учебных ситуаций на уроке, не следует ограничиваться только требованиями и заданиями учебника, полезно предлагать учащимся задания и ставить требования, которые вынуждали бы их проводить самостоятельный опыт.

Оптимизация деятельности учащихся предусматривает создание системы учебных ситуаций, направленных на формирование у учащихся приемов умственной деятельности. Учащиеся, при выполнении учебных задач, учатся наблюдать, запоминать, классифицировать, обобщать признаки.

В общем, предмет выступает перед ребенком как последовательность конкретных явлений. Объяснение учителем каждого из них, объединение готового алгоритма действий приводит к его механическому запоминанию и как результат поверхностного понимания свойств изучаемых явлений- перенос этого алгоритма на подобные по внешним признакам понятия.

В основе всех конкретных проявлений лежит раскрытие сущности, опираясь на эту сущность, ребенок сам получает конкретный случай, учебная деятельность приобретает творческий характер, что обеспечивает не только стремление к дальнейшему обучению, но и развитие творческого мышления.

Важным условием обучения вычислениям является внимание. Выполнение вычислений требует организации внимания учащихся, потому что из-за невнимательности учащиеся допускают много ошибок.

Внимание- это целенаправленность и сосредоточенность сознания , которое предусматривает повышение уровня сенсорной, интеллектуальной или двигательной активности человека. При организации учебно- воспитательного процесса необходимо учитывать все виды внимания.

Психологи выделяют три вида внимания:

1. Внимание притягивает какой-то сильный, необычный ,резкий внезапный раздражитель. Внимание, которое притягивается силой, необычностью раздражителя, носит название непроизвольное. Для младшего школьника наиболее целесообразным является формирование непроизвольного внимания, этого можно добиться, используя разнообразный познавательный материал, эмоциональность.

2. Сосредоточенность на предмете может быть достигнута желанием самого человека, усилием его воли. Он создается тогда, когда человеку приходится преодолевать какие-то трудности, для того, чтобы быть внимательным для чего-то нужного. Такое внимание называют произвольным. Такая разновидность внимания особенно тяжело дается маленьким детям, особенно первоклассникам, потому что требует большого волевого напряжения. Во 2-3 классах некоторые ученики уже имеют произвольное внимание, конкретизируют его на материале учебника или на объяснении учителя. Произвольное внимание очень важно для младшего школьника. Большое значение в формировании произвольного внимания приобретает четкая внешняя организация действий ребенка, сообщение ему таких образцов, указаний на такие внешние способы, пользуясь которыми он может руководить своим сознанием. Произвольное внимание еще нестойкое, дети еще не умеют внутренних способов саморегулирования. Поэтому учитель должен использовать разные виды учебной работы, которые бы сменяли друг друга на уроке и не переутомляли детей. Например, устный счет разными способами, решение задач и проверка результатов, объяснение нового приема письменного вычисления, тренировка его выполнения.

При выполнении простых, но однотипных заданий младшие школьники отвлекаются чаще. Чем при решении более сложных заданий, поэтому необходимо использовать разные способы и приемы работы. Учителю необходимо так организовать разные виды учебной деятельности, чтобы дети приучались к одновременному контролю за несколькими действиями.

П.Я.Гальперин понимает внимание как особенное психическое действие контроля. Он считает, что невнимательность школьников связана с неполной сформированностью функции контроля в таких условиях, когда она складывается стихийно. В связи с этим, задачу планомерного воспитания он видит в постоянном целенаправленном формировании автоматизированных действий умственного контроля.

3. Третьим источником внимания является интерес, то есть отношение человека к какому-нибудь предмету, к своей деятельности, к поставленной задаче, который выражается в желании узнать что-то новое, раскрыть явление глубже и шире.

Такой вид внимания также называется мимолетным, но «второстепенным». В этом случае используется термин «после произвольное внимание».

Произвольное внимание не характерно для младших школьников. Характерным для них является первичное и вторичное непроизвольное внимание.

Для поддержания внимания детей на протяжении урока необходимо придерживаться таких условий организации учебной деятельности:

-удачный темп урока и продуманная его организация;

-четкость, доступность, краткость объяснения;

-максимальная опора на активную умственную деятельность детей;

-хрупкое отношение учителя к вниманию детей;

-смена видов и форм работы;

-включение в деятельность всех учащихся.

Внимание младших школьников характеризуется такими качествами как концентрация, объем, распределение, стойкость.

Концентрация внимания характеризирует силу сосредоточенности человека и определяется той силой нового раздражителя, которая необходима для погашения бывшей доминанты и создания новой.

Большой концентрации внимания детей можно добиться с помощью выделения основного материала, определенных слов-указаний: Запоминай! Вспомни и др.

Например, при изучении темы «Умножение однозначного числа на многозначное» для объяснения используют структурную запись:

3*24= 72

3*20=60

3*4=12

60+12=72

В случаях устного умножения и деления в пределах 1000, Которые сводятся к табличным, выясняют процесс вычисления по структурным записям:

70*8=560 420:7=60

7 дес.*8=56дес. 42дес.:7=6дес.

Объем внимания - это количество объектов, которые человек может одновременно «охватить» с одинаковым качеством. Объем внимания младших школьников ограниченный. Основным условием расширения объема внимания является формирование умений группировать, систематизировать, объединять по сути, воспринятый материал. Например, целесообразно на каждом уроке математики выделять пять минут для проведения зрительного диктанта. Кроме развивающей цели, этот вид работы обеспечит и достижение определенной дидактической цели. Так, записав числа 4,3,7, 0 дети могут:

-составить все возможные числа четвертого десятка;

-с этими числами составить примеры на сложение и вычитание;

-подчеркнуть наибольшее (наименьшее).

Распределение внимания - возможность одновременно успешно выполнять два и более, разных видов деятельности. Умение распределять внимание формируется в процессе овладения деятельностью, оно может быть развито путем упражнений и накопления соответствующих навыков. Распределение внимания формируется путем использования памяток, алгоритмов.

Стойкость- характеристика внимания во времени. Она определяется продолжительностью сохранения внимания. Стойкость характеризуется как длительностью, так и степенью

Концентрации за все время его сохранения.

Стойкость внимания зависит от особенностей объектов сосредоточения и активности личности. Одним из важных условий длительной сосредоточенности, является изменчивость, подвижность объектов внимания. Например, стойкого внимания требует от учеников решение круговых примеров, вычисления «цепочкой».

В процессе обучения приходится иметь дело с двумя формами организации внимания: коллективной и индивидуальной.

При формировании вычислительных навыков каждого ученика в отдельности необходимо учитывать все его психологические особенности. Формой индивидуальной организации внимания является использование алгоритмов, карточек-памяток.

Важным условием формирования вычислительных навыков является память. Память-

отображение прошлого опыта человека, которое проявляется в запоминании и дальнейшем припоминании того, что оно воспринял, почувствовал и о чем думал.

В соответствии содержания того, что человек сохраняет, различают образную, двигательную, эмоциональную и содержательную память.

Память в младшем школьном возрасте под влиянием обучения развивается по двум направлениям:

-усиление значения словесно-логического запоминания;

-овладение возможностью сознательно руководить своей памятью и регулировать ее проявления.

Память состоит из таких процессов:

-запоминание-это закрепление тех образов и выражений , которые создаются под впечатлением предметов и явлений действительности в процессе ощущения и восприятия;

-сохранение- это удержание изученного в памяти;

-воспроизведение-это процесс проявления сознании представлений памяти, ранее воспринятых мыслей, в основе чего лежит оживление следов, возникновения в них возбуждения;

-припоминание -наиболее активное воспроизведение, связанное с напряжением и требующее определённых волевых усилий.

Важную роль в процессе запоминания играет мотивационный компонент. У младших школьников более развита наглядно-образная память, они быстрее запоминают и крепче сохраняют в памяти конкретные сообщения, события, предметы, чем определения и объяснения. Младшие школьники к механическому запоминанию, путем простого преобразования, без осознания существенных связей в пределах запоминаемого материала. Они часто заучивают и воссоздают учебный материал без существенного преобразования. Школьники еще не умеют организовывать содержательного запоминания. Они не умеют разбивать материал на существенные группы, пользоваться логическими схемами, выделять опорные пункты для запоминания.

Эффективность непроизвольного запоминания определяется степенью интеллектуальной активности младших школьников, которая зависит от овладения способами организации и руководства процессом запоминания.

Развивать память помогает заинтересованность материалом. В первую очередь запоминается то, что является важным. Важным в процессе развития памяти является в первую очередь, позитивное отношение к изучаемому материалу. Является очевидной связь памяти и мышления. Но важным является не безсистемное запоминание, а создание определенной системы знаний.

Младшему школьников присущи такие виды памяти:

1. Механическая- основанная на повторении материала без его осознания.

2. Оперативная - вид памяти, которая возникает в процессе выполнения определенной деятельности.

3. Непроизвольная - запоминание без специальной установки.

4. Произвольная, которая основывается на специальной установке.

Основой формирования вычислительных навыков является развитие всех видов памяти.

Формирование вычислительных навыков способствует развитию умственной деятельности учащихся. Мышление социально обусловленный, неразрывно связанный с речью процесс опосредованного и обобщающего отображения действительности в процессе анализа и синтеза.

Мышление- процесс обобщенного познания окружающего мира; заключается в установке закономерных связей и отношений.

Первичной формой существования мышления является мышление в действии, мышление, которое выполняется в действии и в действии выделяется.

Мышление бывает разного типа, а а главным является оперирование пространственными и наглядными образами по цели решения определенных практических задач.

Умственная деятельность совершается с помощью умственных операций: сравнения, анализа и синтеза, абстракции, обобщения и конкретизации и др.

Мышление -сложная и многосторонняя деятельность. Особенности в умственной деятельности ребенка проявляются в различных качествах мышления. Наиболее существенными из них: самостоятельность, широта, глубина, скорость и критичность ума.

Самостоятельность мышления характеризуется умением человека выдвигать новые задачи и находить необходимые решения и ответы, не обращаясь за помощью к другим. Учитель часто встречается с самостоятельностью и несамостоятельностью учеников. Одни ученики легко могут выполнить задания такого типа: найти путь решения задачи нового типа, самостоятельно объяснить новый прием вычисления. Другие ученики без помощи учителя или готового образца, выполнить задания самостоятельно не могут.

Широта мышления выражается в познавательной деятельности, которая объединяет разные области деятельности. Широкая познавательная деятельность, как качество мышления базируется на всесторонних и глубоких знаниях.

Глубина мышления выражается в умении проникать в суть вопросов, видеть проблему там, где у других людей вопросов не возникает. Развитие глубины мышления не возможно без стойких познавательных интересов, стремлению к знаниям.

Гибкость мышления выражается в умении быстро переключаться от одного способа решения задачи на другой. Когда дети вычисляют несколько примеров на сложение, способ действия у них закрепляется, и им сразу тяжело переключиться на вычитание. Поэтому необходимо специально тренировать учащихся на быстрое преобразование действий.

Скорость мышления- это способность человека быстро разбираться в сложных ситуациях, быстро продумать и принять решение.

Способность мыслить постоянно формируется в процессе развития ребенка, развития его познавательной деятельности.

Развитие мышления при изучении вычислительных приемов способствует формированию качеств вычислительных навыков. Бантова М. А. выделяет такие качества вычислительных навыков: правильность, сознательность, обобщенность, рациональность и крепость. Считаю необходимым выделить еще такое качество как скорость вычисления, потому что ее характеристика будет зависеть от от сформированности обобщенности, рациональности и свернутости вычислений.

В своей работе я выделяю три уровня сформированности скорости устных вычислений:

1. Высокий: ученик выполняет одну простейшую математическую операцию не более чем за 4.5 секунды.

2. Средний: ученик выполняет одну простейшую математическую операцию от 4,5 до 6 секунд.

3. Низкий: ученик выполняет одну простейшую математическую операцию более чем 6 секунд.

Развитие мышления, совершенствование умственных операций зависит от методов обучения. Формировать у учеников способность к активному и самостоятельному мышлению – наиболее важная задача учителя.

Итак, гибкую систему вычислительных навыков можно сформировать, если :

- учитель имеет четкое представление о механизме мышления детей, знать его специфику и предусловия развития;

-обучение будет построено на основе систематичности, последовательности и постепенного усложнения практических заданий;

-дополнять систему упражнений такими, которые способствуют формированию внимания, развитию мышления и памяти;

-разработать систему творческих упражнений и познавательных заданий, которые способствуют формированию мотивации вычисления.

1. Типы заданий, направленных на формирование вычислительных навыков в начальной школе

На уроке математики формирование вычислительных навыков занимает большое место. Одной из форм работы по формированию вычислительных навыков являются задания. Овладение вычислительными навыками имеет большое образовательное, воспитательное и практическое значение:

- образовательное значение: устные вычисления помогают усвоить многие вопросы теории арифметических действий, а также лучше понять письменные приемы;

- воспитательное значение: устные вычисления способствуют развитию мышления, памяти, внимания, речи, математической зоркости, наблюдательности и сообразительности;

- практическое значение: быстрота и правильность вычислений необходимы в жизни, особенно когда письменно выполнить действия не представляется возможным (например, при технических расчетах у станка, в поле, при покупке и продаже). 17

В своей работе учителя придерживаются определенных принципов. Один из них (наиболее важный) можно сформулировать следующим образом: работа в классе на каждом уроке должна выполняться всем классом, а не учителем и группой успевающих учеников. То есть необходимо создать такую ситуацию - ситуацию «успеха», при которой каждый ученик смог бы почувствовать себя полноценным участником учебного процесса. Ведь одна из задач учителя заключается не в доказательстве незнания или слабого знания ученика, а во вселении веры в ребенка, что он может учиться лучше, что у него получается. Нужно помочь ребенку поверить в собственные силы, мотивировать его на учебу.

Рассмотрим основные типы заданий:

1. Задания с использованием сравнений:

Для активизации познавательной деятельности учащихся при формировании вычислительных можно использовать метод наблюдений. В процессе наблюдения учащиеся сравнивают, анализируют, делают выводы. Полученные таким образом знания являются более осознанными и тем самым лучше усваиваются.

В качестве примера рассмотрим изучение такого вопроса, как изменение суммы в зависимости от изменения одного из слагаемых. В основе познания учениками данной зависимости лежит прием сравнения.

Задание 1. Решите примеры и сравните их:

2 + 1, 2 + 2.

Необходимо обращать внимание учеников на то, что в одном и в другом примере стоит знак «+», а первые слагаемые одинаковы. Эти примеры схожи. Затем выявляются различия: в первом примере второе слагаемое равно 1, во втором 2, сумма в первом примере равна 3, а во втором – 4.

Ребята отмечают, что во втором примере прибавляем большее (2 1), поэтому и получаем большую сумму.

Переходя к сравнению выражений подбираем такие выражения, в которых ученики смогут усмотреть различные признаки различия и сходства.

Задание 2. На доске записаны примеры:

5 + 3, 4 + 3, 8 – 3, 6 + 3, 7 – 3, 9 – 3

Угадайте сходство или различие записанных выражений. Ученики обычно указывают такие признаки сходства, как знак действия, затем обращают внимание на то, что в первой группе прибавляется число 3, а во второй – вычитается число 3. Затем целесообразно поставить вопрос: «Что произойдет с ответами примеров в первой группе и во второй? Почему ответы в первой группе больше, чем ответы во второй?»

Очень полезно задание и такое:

Задание 3. Что вы замечаете в данных примерах?

1 + 1, 2 + 1, 3 + 1, 4 + 1, 6 + 1, 7 + 1

Ученики должны обратить внимание не только на тот факт, что во всех примерах знак «+» и второе слагаемое везде равно 1, но и на то, что последовательность 1, 2, 3, 4 … нарушена, т.к. пропущен пример 5 + 1.

Подобные задания способствуют развитию математической наблюдательности учеников, их умению видеть сходства и различия, выявлять определенные закономерности. В процессе выполнения таких заданий уясняется смысл понятия «сравнить».

Так же могут предлагаться задания с ошибками, которые требуют исправления:

Задание 4. Найди ошибку:

Могут предлагаться задания, у которых уже дан знак отношения и одно из выражений, а другое выражение надо составить или дополнить:

8 · (10 + 2)=8 · 10 + …

Выражения таких заданий могут включать различный числовой материал: однозначные, двузначные, трехзначные числа и величины. Выражения могут быть с разными действиями.

Главная роль таких заданий – способствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах, о неравенствах и др. Также они помогают выработке вычислительных навыков.

1. Задания на классификацию и систематизацию знаний.

Умение выделять признаки предметов и устанавливать между ними сходство и различие - основа заданий на классификацию. Из курса математики известно, что при разбиении множества на классы необходимо выполнять следующие условия:

1) ни одно из подмножеств не пусто;

2) подмножества попарно не пересекаются;

3) объединение всех подмножеств составляет данное множество.

Предлагая детям задания на классификацию, эти условия необходимо учитывать.

Задание 1. Найди значения разностей

742 - 531 898 - 769

374 - 223 586 - 218

457 -132 465 -427

По какому признаку распределены разности по этим столбикам?

1. Задания на выявление общего и различного.

Выделение существенных признаков математических объектов, их свойств и отношений - основная характеристика таких заданий. Благодаря им учащиеся могут самостоятельно «открывать» математические свойства и способы действий (правила), которые в математике строго доказываются.

Задание 1. Рассмотрите рисунок и попробуйте быстро подсчитать, сколько окон в доме.

Дети могут предложить следующие способы: 3+3+3+3, 4+4+4 или 3*4=12; 4*3=12.

Учитель предлагает сравнить полученные равенства, т. е. выявить их сходство и различие. Отмечается, что оба произведения одинаковые, а множители переставлены.

Вывод: «Если множители переставить, то произведение не изменится» или «От перестановки множителей значение произведения не изменится».

1. Задания с многовариантными решениями.

Многовариантные задания - это система упражнений, выполнение которых поможет глубоко и осознано усвоить правило и выработать необходимый вычислительный навык на его основе.

Задание 1. Запиши число 30 тремя одинаковыми цифрами и знаками действий.

Постарайся найти несколько разных решений.

Задание 2. Какое число надо прибавить к 25, чтобы получить круглое?

1. Задания с элементами занимательности.

Такие задания, в основном, направлены на отработку вычислительных навыков. Элемент занимательности увлекает детей, они стремятся выполнить все действия правильно и посмотреть к чему это приведет.

"Магические или занимательные квадраты" - это занимательная форма тренировки в сложении вычитания и размещения чисел. Решение магических квадратов увлекает школьников всех возрастов.

1. Задания на нахождение значений математических выражений.

Предлагается в той или иной форме математическое выражение, требуется найти его значение. Эти задания имеют много вариантов. Можно предлагать числовые математические выражения и буквенные (выражение с переменной), при этом буквам придают числовые значения и находят числовое значение полученного выражения, например:

- найдите разность чисел 100 и 9.

- найдите значение выражения С – К, если С = 100, К = 9.

Выражения могут предлагаться в разной словесной форме:

- из 100 – 9; 100 минус 9

- уменьшаемое 100, вычитаемое 9, найдите разность

- найти разность чисел 100 и 9

- уменьшить 100 на 9 и т.д.

Эти формулировки использует не только учитель, но и ученики.

Выражения могут быть даны с ошибками, которые детям предстоит найти:

Задание 1. Найди ошибки в выражениях:

Выражения могут включать одно и более действий. Выражения с несколькими действиями могут включать действия одной ступени или разных ступеней, например:

47 + 24 – 56

72 : 12 · 9

400 – 7 · 4 и др.

Могут быть со скобками или без скобок: (90 – 42) : 3, 90 – 42 : 3. Как и выражения в одно действие, выражения в несколько действий имеют разную словесную формулировку, например:

- из 90 вычесть частное чисел 42 и 3

- уменьшаемое 90, а вычитаемое выражено частным чисел 42 и 3.

Выражения могут быть заданы в разной области чисел: с однозначными числами

(7 – 4), с двузначными (70 – 40, 72 – 48), с трехзначными (700 – 400, 720 – 480) и т.д., с натуральными числами и величинами (200 – 15, 2м – 15см). Однако, как правило, приёмы устных вычислений должны сводиться к действиям над числами в пределах 100. Так, случай вычитания четырехзначных чисел 7200 – 4800 сводится к вычитанию двузначных чисел (72сотни – 48сотен) и значит его можно предлагать для устных вычислений.

Выражения можно давать и в форме таблицы:

Задание 2. Заполни таблицы:

Уменьшаемое	12	14	15	17	28
Вычитаемое	10	10	10	10	10
Разность

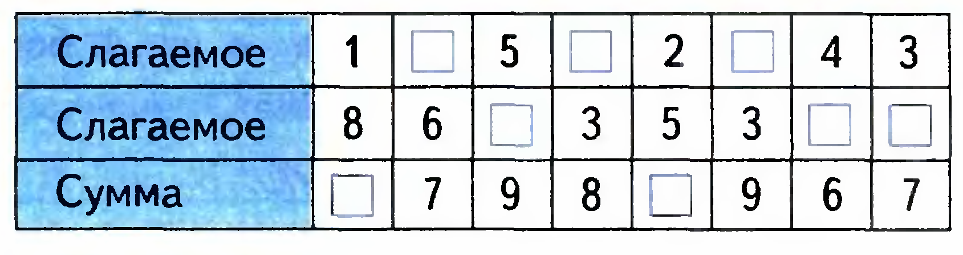
Так же такие задания могут быть представлены в виде раз личных «цепочек»:

Задание 3: Реши цепочки:

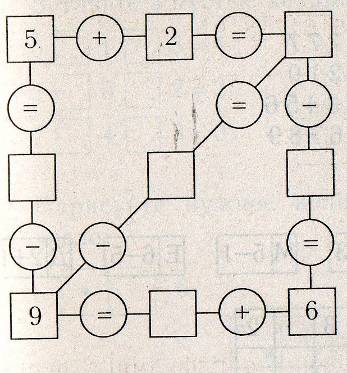
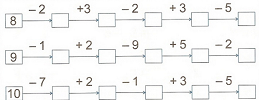
Основное значение заданий на нахождение значений выражений – выработать у учащихся твердые вычислительные навыки, а также они способствуют усвоению вопросов теории арифметических действий.

Могут предлагаться задания, у которых уже дан знак отношения и одно из выражений, а другое выражение надо составить или дополнить:

8 · (10 + 2)=8 · 10 + …

Выражения таких заданий могут включать различный числовой материал: однозначные, двузначные, трехзначные числа и величины. Выражения могут быть с разными действиями.

Главная роль таких заданий – способствовать усвоению теоретических знаний об арифметических действиях, их свойствах, о равенствах, о неравенствах и др. Также они помогают выработке вычислительных навыков.

1. Комбинаторные задачи.

Комбинаторика - один из разделов современной математики.

Комбинаторные задачи служат средством развития мышления детей, воспитания у них умения применять полученные знания в различных ситуациях посредством выработки навыков и повторения пройденного. Умение выполнять разбиение множеств, составлять комбинации по определенным признакам и классифицировать лежит в основе разнообразных сфер человеческой деятельности.

Задание 1. При умножении двух однозначных чисел получилось число 16

Чему были равны множители?

Найди всевозможные решения.

Задание 2. На складе находилось 7 полных бочонков меда, 7 наполовину заполненных медом и 7 пустых бочонков. Как распределить все бочонки между тремя покупателями так, чтобы каждый получил одинаковое количество меда и бочонков. (мед не нужно перекладывать из одного бочонка в другой.)

Использование на уроках математики заданий различного типа возбуждает у детей интерес, стимулирует их к активной деятельности и позволяет более прочно сформировать вычислительные навыки.

2 ОРГАНИЗАЦИЯ ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ ПО ФОРМИРОВАНИЮ ВЫЧИСЛИТЕЛЬНЫХ НАВЫКОВ У УЧАЩИХСЯ 2 КЛАССА НА УРОКАХ МАТЕМАТИКИ

2.1. Констатирующий этап (выявление исходного уровня сформированности вычислительных навыков у учащихся 2 класса)

Опытно-экспериментиальная работа проводилась в МОУ-СОШ с. Кирово во 2 классе. Во 2 классе 4 человека.

Цель констатирующего этапа – определить исходныйуровень сформированности вычислительных навыков у детей младшего школьного возраста.

Задачи этапа:

- определить критерии и показатели уровня сформированности вычислительных навыков у младших школьников;

- подобрать диагностический инструментарий;

- провести наблюдение за учащимися;

- провести анализ полученных данных.

Важным условием диагностики уровня сформированности вычислительных навыков является определение критериев сформированности навыков и их показателей.

Для нашей работы в качестве таких критериев мы взяли объем (количество) и качество. Рассмотрим эти критерии и их показатели.

Таблица1

Диагностический инструментарий для определения уровня сформированности вычислительных навыков.

Критетии	Показатели	Диагностический инструментарий
Объем (количество)	Количество усвоенных вычислительных приемов	Самостоятельная работа; наблюдение
Качество	а) осознанность выполнения операций б)правильность (соответствие сформированных навыков учащихся требуемым нормам	Наблюдение Самостоятельная работа

Диагностировались следующие вычислительные приемы:

- сложение двузначных чисел без перехода через разряд;

- вычитание двузначных чисел без перехода через разряд;

- сложение двузначных чисел с переходом через разряд;

- вычитание двузначных чисел с переходом через разряд;

- сложение трехзначных чисел без перехода через разряд;

- вычитание трехзначных чисел без перехода через разряд.

Характеристика уровней:

Низкий уровень (0 – 13) – ученик часто неверно находит результат арифметических действий, неправильно выбирает и выполняет операции; ребенок не осознает порядок выполнения операций; количество усвоенных приемов – менее трех.

Средний уровень (14 – 21) – ребенок иногда допускает ошибки в промежуточных операциях; осознает, на основе каких знаний выбраны операции, но не может самостоятельно объяснить, почему решал так, а не иначе; количество усвоенных приемов – 3 – 4.

Высокий уровень (22 – 25) – ученик правильно находит результат арифметического действия над данными числами; осознает, на основе каких знаний выбраны операции, может объяснить решение примера. Количество усвоенных приемов – 5 – 6.

Для выявления уровня сформированности у учащихся вычислительных навыков были использованы методы исследования, выбор которых был обусловлен поставленными задачами. Нами была разработана самостоятельная работа, направленная на изучение уровня сформированности вычислительных навыков и на выявление количества усвоенных приемов. Учитывая, что по результатам одной самостоятельной работы нельзя сделать конкретных выводов об уровне сформированности вычислительных навыков в экспериментальном классе, нами было проведено наблюдение, целью которого стало не только выявление количества и качества усвоенных приемов..

Таблица 2

Примеры заданий для самостоятельной работы

Задания	Проверяемый вычислительный навык или прием
Сравни выражения не вычисляя их значения: 64 + 2 … 58 + 2 73 – 3 …. 73 – 1 145 + 52… 52+ 145	Осознанность вычислительных действий (могут ли не вычисляя значение выражений дать верный ответ)
Реши письменно примеры, подробно записывая ход своих рассуждений: 54 – 26 28 + 29 47 – 19 55 + 37	Сложение и вычитание двузначных чисел с переходом через разряд
Реши: 69 – 28 71 + 26 576 – 215 785 + 111	Сложение и вычитание двузначных и трехзначных чисел без перехода через разряд;
4. От крышки стола отпилили угол. Сколько осталось углов?	Осознанность вычислительных действий

За задание №1 учащиеся могли получить 3 балла (по 1 баллу за каждый пример). Задание №2 оценивалось в 8 баллов (по 2 балла за правильно решенное выражение). За задание №3 учащиеся максимально могли получить 8 балла (2 балла за решенное выражение). За задание №4 давалось 2 балла. Таким образом, максимально учащиеся могли заработать 21балл. За вычислительные ошибки снималось по 1 баллу.

Полученные результаты оценивалась по трем уровням: высокий (19 – 21 баллов), средний (11 – 18 баллов), низкий (0-10 баллов).

Таблица 3.

Результаты самостоятельной работы.

Ф.И.	Осознанность вычислительных действий (макс. 5)	Сложение двузначных чисел без перехода через разряд (макс. 2)	Вычитание двузначных чисел без перехода через разряд (макс. 2)	Сложение двузначных чисел с переходом через разряд (макс. 4)	Вычитание двузначных чисел с переходом через разряд (макс. 4)	Сложение трехзначных чисел без перехода через разряд (макс. 2)	Вычитание трехзначных чисел без перехода через разряд (макс. 2)	Общий балл макс. 21)
Бобров С.	3	2	2	4	2	0	2	15
Лоскутов М.	2	2	2	2	0	2	0	10
Мыльников А.	4	2	2	2	0	2	2	14
Энютин А.	2	2	2	4	2	2	2	16

В ходе проверки самостоятельных работ выяснилось, что с заданием №1 справились почти все учащиеся, кроме Лоскутова М., который при выполнении №1 нарушили правило выполнения задания, т.е. он дали верный ответ, предварительно вычислив значения выражений. С заданием №4 не справился 1 ученик – Алексей Э. Остальные учащиеся правильно выполнили №4. При выполнении задания №2 большинство детей допускали ошибки в примерах на вычитание двузначных чисел с переходом через разряд. С этим заданием частично справились только двое учеников Сапша Б. и Лёша Э. Двое учащихся не справились с данным заданием. С заданием №3 правильно справились двое учащиеся, двое учащихся допустили вычислительные ошибке при счёте.

Таким образом, по результатам самостоятельной работы низкий уровень сформированности вычислительных навыков наблюдался у Матвея Л., высокий уровень не выявился у учащихся. Средний уровень сформированности вычислительных навыков у трёх учащихся Алексея Э., Александра Б., Алексея М.

Кроме самостоятельной работы, нами использовался метод наблюдения. Его целью было пронаблюдать за работай детей у доски, их рассуждениями. Максимально учащиеся могли получить 4 балла. Наблюдение проводилось на уроках математики.

Таблица 4.

Протокол наблюдения

№ п/п	ФИ детей	Параметры наблюдения						Общий балл
		Правильно выполняет вычисления	Объясняет решение примера	Не всегда может объяснить выбор операции	Допускает ошибки в вычислениях	Вычисления выполняет неправильно	Не может объяснить выбор операции
1	Бобров А.	2	2					4
2	Лоскутов М.			1	1			2
3	Мыльников А.			1	1			2
4	Энютин А.	2	2					4

0 – показатель отсутствует;

1 – 2 – показатель присутствует частично;

3 – 4 – показатель присутствует.

В результате наблюдения за работой учащихся на уроке математики выяснилось, что показатель сформированности вычислительных навыков присутствует у двух учащихся – Боброва А., Энютина А.. Эти учащиеся правильно выполняют вычисления, могут объяснить ход своих рассуждений. У остальных учащихся показатель сформированности навыков присутствует частично (средний уровень). Таким образом, на констатирующем этапе эксперимента, мы установили, что у двоих учащихся класса низкий уровень сформированности знаний, у двоих учащихся – средний уровень.

Результаты покажем в таблице 5 и на рисунке 1.

Таблица 5

№ п/п	Ф.И.	Общее количество баллов	Уровень
1	Бобров А.	19	Средний
2	Лоскутов М.	12	Низкий
3	Мыльников А.	16	Средний
4	Энютин А.	20	Средний

Рисунок 1.

Из диаграммы видно, что детей с низким уровнем сформированности вычислительных навыков- 25 %, со среднем уровнем - 75 %, с высоким – 0 %.

Таким образом, на основе полученных результатов, можем сделать вывод о том, что в данном классе сформированность вычислительных навыков на среднем уровне. Большинство учащихся допускают в вычислениях ошибки, связанные со сложением и вычитанием с переходом через разряд, а так же не всегда могут объяснить решение примера. Осознанность вычислительных действий сформирована в достаточной степени – большинство учащихся данного класса могут объяснить выбор операций при решении примера, так же почти все дети могут сравнивать выражения с одинаковым слагаемым, уменьшаемым или вычитаемым не вычисляя их значение. Всего двое учащихся класса выполняют вычисления правильно, без ошибок, что говорит о необходимости совершенствования вычислительных навыков. Поэтому необходимо разработать совокупность заданий, направленных на совершенствование и развитие необходимых вычислительных навыков, и включить их в учебный процесс 2 класса.

2.2 Формирующий этап (работа по формированию вычислительных навыков у учащихся 2 класса

На основе результатов, полученных в ходе констатирующего эксперимента, нами была разработана совокупность заданий, направленных на улучшение качества сформированных знаний и увеличение количества усвоенных вычислительных приемов. Задания включались в уроки математики на различных этапах их проведения.

Таблица 6

Программа включения заданий на формирование вычислительных навыков в уроки математики

Тема урока	Вид задания	Формируемый вычислительный прием
Сложение трехзначных чисел с переходом через разряд	Нахождение значений выражений. Задания на классификацию	Сложение и вычитание двузначных чисел без перехода через разряд и с переходом
Вычитание трехзначных чисел с переходом через разряд	Нахождение значений выражений и сравнений этих значений	Вычитание двузначных чисел без перехода через разряд и с переходом.
Обратные операции	Нахождение значения выражений Многовариантные задания	Сложение двузначных чисел с переходом через разряд и без перехода Осознанность
Длина ломаной. Периметр	Сравнение выражений с переменной. Нахождение значения выражений по цепочке.	Осознанность вычислительных действий. Сложение с переходом через разряд и без перехода.
Порядок выполнения действий в выражениях	Нахождение значения выражений	Сложение и вычитание двузначных чисел с переходом через разряд
Виды алгоритмов.	Нахождение значения выражений (по алгоритму)	Сложение двузначных чисел с переходом через разряд и без перехода
Угол. Прямой угол.	Нахождение значений выражений с элементом занимательности	Сложение и вычитание с переходом через разряд
Свойства сложения	Нахождение значений выражений с элементом занимательности	Сложение двузначных чисел с переходом через разряд. Сложение двузначных и трехзначных чисел без перехода через разряд Осознанность
Вычитание суммы из числа	Нахождение значения выражений	Вычитание двузначных чисел из трехзначных с переходом через разряд. Сложение двузначных чисел с переходом через разряд
Вычитание числа из суммы.	Задания с многовариантными решениями с элементом занимательности	Сложение и вычитание двузначных чисел с переходом через разряд

Приведем примеры включения заданий в уроки математики:

На уроке по теме «Сложение трехзначных чисел с переходом через разряд» на этапе актуализации знаний учитель предлагает учащимся следующее задание:

Найдите значение выражений:

34 + 12 84 + 15 56 + 27 67 + 32

48 – 29 23 – 14 92 – 35 75 - 38

Разделите данные выражения на две группы. По какому признаку вы разделили данные выражения?

При разделении данных выражений, учащиеся будут выделять вычислительные приемы, на которых они основаны. При этом они повторяют приемы сложения и вычитания с переходом через разряд и без перехода и осознают правила, на которых они основаны. Выполняя такие задания, дети определяют, какие из них относятся к группе вычислений с переходом через разряд, а какие без перехода. Такие задания подготавливают детей к более сложной работе (сложение трехзначных чисел с переходом через разряд).

На уроке по теме «Обратные операции» на этапе закрепления учитель предлагает учащимся следующее задание:

Найдите значение выражений.

42 + 30 57 + 12 67 + 19 24 + 78

К каждому равенству напишите все возможные равенства с обратным действием. Какое это действие?

Выполняя такое задание, у детей закрепляется вычислительный навык сложения с переходом через разряд и без перехода. Так же формируется осознанность, т.к. при выполнении такого задания, детям нужно записать выражения с обратными действиями, что требует от детей понимания взаимосвязи между компонентами и результатом действий сложения и вычитания.

На уроке по теме «Виды алгоритмов» на этапе изучения нового материала учитель включает следующие задания:

Пользуясь алгоритмом сложения двузначных чисел, вычисли суммы:

25 + 32 + 14 16 + 28 + 50

43 + 34 + 70 81 + 39 + 87

Выполняя подобное задание, дети отрабатывают прием сложения двузначных чисел с переходом через разряд и без перехода. Действуя строго по алгоритму, дети более прочно усваивают данные приемы, т.к. неверные вычисления приводят к неверному решению алгоритма, и значит решать придется сначала. Многократное повторение вычислительных действий способствует более прочному усвоению вычислительного приема.

На уроке по теме «Свойства сложения» на этапе работы по новой теме учитель предлагает детям найти равные выражения и вычислить их значение удобным способом.

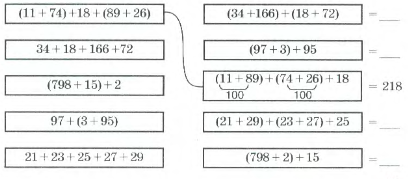
Какие свойства сложения были использованы для упрощения вычислений?

При работе с подобным заданием перед детьми стоит не только задача вычислить значение выражений, но и упростить процесс вычислений, используя свойства сложений, которые лежат в основе вычислительных приемов сложения с переходом через разряд и без перехода. Дети повторяют и закрепляют эти приемы. В результате многократного использования данных приемов, дети более прочно и осознано усваивают их.

На уроке по теме «Вычитание числа из суммы» на этапе закрепления учитель может предложить детям поиграть в «Лабиринт». Детям предлагается найти все возможные варианты «выхода» из лабиринта.

Выполнение этого задания требует от детей внимательных и осознанных вычислений. Т. к. решений может быть несколько, детям предстоит не один раз пройти «лабиринты», находя то верные, то неверные пути, что приводит к закреплению приемов сложения и вычитания с переходом через разряд и без перехода.

Включение подобных заданий в уроки математики, на разных этапах их проведения, позволяет сформировать у учащихся более прочные и осознанные вычислительные навыки. Частое повторение одного и того же вычислительного приема способствует улучшению качества и количества сформированных вычислительных приемов.

2.3. Контрольный этап (повторная диагностика и сравнительный анализ результатов относительно первого этапа)

 

На контрольном этапе опытно-экспериментальной работы мы провели повторную диагностику уровня сформированности вычислительных навыков у учащихся 2 класса. При этом применялись те же методики, что на констатирующем этапе.

Результаты занесены в таблицу:

Таблица № 7

Результаты самостоятельной работы.

Ф.И.	Осознанность вычислительных действий (макс. 5)	Сложение двузначных чисел без перехода через разряд (макс. 2)	Вычитание двузначных чисел без перехода через разряд (макс. 2)	Сложение двузначных чисел с переходом через разряд (макс. 4)	Вычитание двузначных чисел с переходом через разряд (макс. 4)	Сложение трехзначных чисел без перехода через разряд (макс. 2)	Вычитание трехзначных чисел без перехода через разряд (макс. 2)	Общий балл макс. 21)
Бобров С.	5	2	2	4	4	2	2	21
Лоскутов М.	2	2	2	2	2	2	2	14
Мыльников А.	4	2	2	2	0	2	2	14
Энютин А.	5	2	2	4	4	2	2	21

Таким образом, по результатам самостоятельной работы средний уровень сформированности вычислительных навыков наблюдался у Матвея Л. и Мыльникова А., высокий уровень был сформирован у двух учащихся Алексея Э., Александра Б.

Кроме самостоятельной работы, мы также использовали метод наблюдения. Его целью было пронаблюдать за работай детей у доски, их рассуждениями. Максимально учащиеся могли получить 4 балла. Наблюдение проводилось на уроках математики.

Таблица 4.

Протокол наблюдения

№ п/п	ФИ детей	Параметры наблюдения						Общий балл
		Правильно выполняет вычисления	Объясняет решение примера	Не всегда может объяснить выбор операции	Допускает ошибки в вычислениях	Вычисления выполняет неправильно	Не может объяснить выбор операции
1	Бобров А.	2	2					4
2	Лоскутов М.			1	1			2
3	Мыльников А.			1	1			2
4	Энютин А.	2	2					4

0 – показатель отсутствует;

1 – 2 – показатель присутствует частично;

3 – 4 – показатель присутствует.

В результате наблюдения за работой учащихся на уроке математики выяснилось, что показатель сформированности вычислительных навыков присутствует у двух учащихся – Боброва А., Энютина А.. Эти учащиеся правильно выполняют вычисления, могут объяснить ход своих рассуждений. У остальных учащихся показатель сформированности навыков присутствует частично (средний уровень). Таким образом, на констатирующем этапе эксперимента, мы установили, что у двоих учащихся класса низкий уровень сформированности знаний, у двоих учащихся – средний уровень.

Результаты покажем в таблице 8 и на рисунке 1.

Таблица 5

№ п/п	Ф.И.	Общее количество баллов	Уровень
1	Бобров А.	25	Высокий
2	Лоскутов М.	16	Средний
3	Мыльников А.	16	Средний
4	Энютин А.	25	Высокий

Рисунок 2.

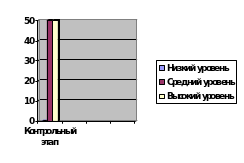
Из диаграммы видно, что на контрольном этапе детей с низким уровнем сформированности вычислительных навыков- 0 %, со средним уровнем - 50 %, с высоким – 50 %.

Сравним полученные результаты на констатирующем и контрольном этапах диагностики сформированности вычислительных навыков учащихся 2 класса:

Рисунок 3.

Сравнив результаты опытно-экспериментальной работы, отмечаем положительную динамику уровня сформированности вычислительных навыков. Так как детей с низким уровнем сформированности вычислительных навыков стало на 25% меньше, а детей с высоким уровнем на 50% больше, так как двое учащихся со средним уровнем на контрольной диагностике показали высокие результаты.

Таким образом, наблюдая положительные изменения, можно сделать вывод о том, что проделанная нами работа была эффективной.

ЗАКЛЮЧЕНИЕ

Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в начальной школе, поскольку вычислительные навыки необходимы при изучении арифметических действий. Школа всегда уделяла большое внимание проблеме формирования прочных и осознанных вычислительных умений и навыков, так как содержательную основу начального математического образования оставляют понятия числа и четырех арифметический действий. Программы по математике включают большой интересный материал по проблеме формирования прочных навыков вычислений, однако, по-прежнему некоторые вопросы понимания и отработки навыка арифметических вычислений являются для младших школьников довольно сложными.

В процессе работы по теме «Формирование вычислительных навыков у младших школьников на уроках математики» нами было охарактеризовано понятии «вычислительный навык» и выделены этапы его формирования (подготовка к введению нового приема, ознакомление с вычислительным приемом, закрепление знаний приема и выработка вычислительного навыка). Так же нами были выбраны и рассмотрены типы заданий, направленных на формирование вычислительных навыков (задания с использованием сравнений, задания на классификацию и систематизацию знаний, задания на выявление общего и различного, задания с многовариантными решениями, задания с элементами занимательности, комбинаторные задачи). Нами было отмечено, что использование выбранных типов заданий на уроках математики возбуждает у детей интерес к предмету, стимулирует их к активной деятельности и позволяет более прочно сформировать вычислительные навыки.

В ходе проведенной нами опытно-экспериментальной работы по изучению уровня сформированности вычислительных навыков у учащихся 2 класса, мы выяснили, что вычислительные навыки в экспериментальном классе сформированы на среднем уровне, а так же, что большинство детей способны объяснить логику выполнения той или иной операции и обосновать свой выбор вычислительного приема. Однако, нами было установлено, что многие дети довольно часто допускают ошибки при вычислении в приемах на сложение и вычитание с переходом через разряд.

Основываясь на результатах, полученных в ходе проведения экспериментальной работы, нами была разработана система заданий, способствующих совершенствованию вычислительных навыков, а так же направленных на увеличение количества сформированных вычислительных приемов. Эти задания включались в уроки математики на различных этапах их проведения.

Результатом такой работы стало формирование у учащихся экспериментального класса более прочных и осознанных вычислительных навыков. Так же эти задания способствовали увеличению количества сформированных вычислительных приемов.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Актуальные проблемы методики обучения математике в начальных классах / Под ред. М.И.Моро, А.М. Пышкало. — М.: Педагогика, 1977. — 248 с.

2. Аргинская, И.И., Ивановская, Е.И Математика 2 класс. Часть 1. – С.:, Издательство «Корпорация Федоров», 2010 – 128 с.

1. Бадма – Гаряева, М.В. Развитие вычислительных навыкову учащихся 1 класса // Начальная школа – 1999 – №11 – с.21 – 23

2. Бантова, М. А., Бельтюкова, Г. В. Методика преподавания математики в нач. классах: Учеб. пособие для уч-ся школ. отд-ний пед. уч-щ / Под ред. М. А. Бантовой. - 3-е изд. - М.: Просвещение,1984. - 335 с.

3. Бантова, М. А. Система формирования вычислительных навыков // Начальная

школа – 1993 - №11 – с. 38 – 43

1. Бахир, В. К. Развивающее обучение // Начальная школа – 1997 - №5 – с. 26 – 31

2. Давыдов, В. В. Проблемы развивающего обучения: опыт теоретического и

экспериментального психологического исследования. – М.: Педагогика, 1986 – 239 с.

1. Давыдов, В. В. Содержание и строение учебной деятельности школьников. – М., 1978 – 321 с.

2. Давыдов, В.В. Теория развивающего обучения. – М.: ИНТОР, 1996 – 544 с.

3. Давыдов, В. В. Что такое учебная деятельность // Начальная школа – 1999 - №7 – с. 12 – 18

4. Зимняя, И. А. Педагогическая психология. – Ростов на Дону: Феникс, 1997 – 476 с.

5. Ильина, О. Н. Проблема формирования вычислительных навыков младших школьников в современных условиях // Интернет журнал СахГУ «Наука, образование, общество». – 2006. - 3 февраля. URL статьи: http://journal.sakhgu.ru.

6. Истомина, Н.Б. Методика обучения математике в начальных классах. – М., 1997

7. Клецкина, А.А. Организация вычислительной деятельности младших школьников в системе развивающего обучения // Автореферат диссертации на соискание ученой степени канд. пед. наук. — М., 2001. — 20 с.

8. Лавлинская, Е.Ю. Методика формирования вычислительного навыка по системе общего развития Занкова Л.В. – В.: Панорама, 2006.- с.176.

9. Мельникова, Н. А. Развитие вычислительной культуры учащихся // Математика в школе.- 2001.- №18.- С. 9-14.

10. Менчинская, Н. А. Моро М. И. Вопросы методики и психологии обучения арифметики в начальных классах.- М.: Просвещение, 1965.- 224 с.

11. Методика начального обучения математике: Учеб. пособие для студентов пед. ин-тов по спец-ти «Педагогика и методика начального обучения» // Под ред. Л. Н. Скаткина. – М.: просвещение, 1972.- 320с.

12. Моро, М.И., Бантова, М.А., Бельтюкова, Г.В. Математика 2 класс. В 2 ч. Ч.1 – М.: Просвещение, 2009 – 96 с.: ил.

13. Моро, М.И., Бантова, М.А., Бельтюкова, Г.В. Математика 2 класс. В 2 ч. Ч.1 – М.: Просвещение, 2009 – 96 с: ил.

14. Петерсон, Л.Г. Математика. 2 класс. Часть 1. – М.: Издательство «Юнента», 2005. 80 с.: ил.

15. Петерсон, Л.Г. Математика. 2 класс. Часть 2. – М.: Издательство «Юнента», 2005. 112 с.: ил.

16. Реализация межпредметных и внутрипредметных связей в обучении и воспитании младших школьников: Межвузовский сборник научных трудов. –

Л., 1984 – 132 с.

1. Репкина, Г.В. Заика Е.В. Оценка уровня сформированности учебной деятельности. Томск: Пеленг, 1993 – 62 с.

2. Федотова, Л. Повышение вычислительной культуры учащихся // Математика в школе. - 2004. - №35. - С. 3-7.

3. Федотова, Л. Повышение вычислительной культуры учащихся // Математика в школе. - 2004. - №43. - С. 2-5.

69