Министерство образования и науки Республики Бурятия
Муниципальное образование Кяхтинский район
МБОУ Малокударинская СОШ
Исследовательская работа
Квадраты-матрёшки
Выполнила ученица 10 класса Соболева Екатерина
Руководитель учитель Красикова Татьяна Ильинична
Введение.
Ежедневно, в процессе своей жизнедеятельности, человеку приходиться выполнять множество математических операций: рассчитывать свое время, что-то считать, что-то измерять, производить оплату за проезд, услуги, за товар и т.д. Для этого человек, не задумываясь, использует и целые, и дробные, и четные, и нечетные, и простые, и другие числа. Однако, каждая из этих категорий для определенных математических практических приложений имеет большое значение. Обратим свое внимание на такую категорию как простые числа. Картину теории распределения простых чисел начали писать еще до нашей эры, незакончена она и на сегодняшний день.
Актуальность. В современном мире интерес к простым числам не ослабевает. Ведется поиск простых чисел с большим количеством цифр. Прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются Пифагоровыми треугольниками, а числа: 3,4,5 – Пифагоровыми тройками. Применение Пифагоровых троек освещено в школьном курсе недостаточно. Материалы исследования могут быть использованы учениками и учителями при преподавании курса геометрии.
Цель работы: показать уникальность открытия Пифагора и дать определение понятия примитивных пифагоровых троек, описать простые способы формирования пифагоровых троек и их применения для вписывания одного квадрата в другой.
Для достижения поставленной цели предусматриваем решение следующих задач:
отобрать материал для исследования, выбрать главную, интересную, понятную информацию;
проанализировать и систематизировать полученную информацию;
подобрать наиболее интересные, наглядные примеры.
Методы исследования:
Пифагоровы тройки и их значение.
Пифагоровой тройкой называется комбинация из трех целых чисел
a,b,c , удовлетворяющих условию
c2 = a2 + b2. Примитивными являются те из них, которые не могут быть получены из других путем умножения на одно и то же число.
Из определения следует, что a,b и c являются взаимно простыми числами.
Согласно теореме Пифагора эти числа могут служить длинами некоторого прямоугольного треугольника; поэтому а и в называют «катетами», а с – « гипотенузой».
Формула Евклида является основным средством построения пифагоровых троек. Согласно ей для любой пары чисел m и n (m n) целые числа a = m2 – n2, b = 2mn,
c = m2 + n2 образуют пифагорову тройку. Тройки, образованные по формуле Евклида, примитивны тогда и только тогда, когда m и n взаимно просты и m – n нечетно. Если и m и n нечетны, то a, b и c будут четными и тройка не примитивна. Однако деление a, b и c на 2 дает примитивную тройку, если m и n взаимно просты.
Любая примитивная тройка получается из единственной пары взаимно простых чисел m и n, оно из которых четно. Отсюда следует, что существует бесконечно много примитивных пифагоровых троек.
Несмотря на то, что формула Евклида генерирует все примитивные простые тройки, она не порождает все тройки. При дополнении дополнительного параметра k получается формула, порождающая все пифагоровы треугольники единственным образом:
a = k ∙ (m2 – n2), b = k ∙ (2mn), c = k ∙ (m2 + n2),
где m, n и k – натуральные числа, m n, m – n нечетно, m и n взаимно просты.
То, что эти формулы образуют пифагоровы тройки, можно проверить путем подстановки в a2 + b2 и проверки, что результат совпадает с c2. Поскольку любую пифагорову тройку можно разделить на некоторое число k, чтобы получить примитивную тройку, любая тройка может быть образована единственным образом с использованием m и n для создания примитивной тройки, а затем она умножается на k.
Доказательство формулы Евклида (приложение 1)
Свойства пифагоровых троек
Свойство 1. Числа, входящие в простейшую пифагорову тройку, попарно взаимно просты.
Следствие. В простейшей пифагоровой тройке только одно число может быть чётным.
Свойство 2. В простейшей пифагоровой тройке числа m и n не могут быть одновременно нечётными.
Пифагоровы тройки находят прямое применение в проектировании множества вещей, окружающих нас в повседневной жизни. А умы учёных продолжают искать новые варианты доказательств теоремы Пифагора.
История того, что существуют числа, которые не делятся ни на какое другое число, люди знали еще в древности. Последовательность простых чисел имеет примерно следующий вид: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 … Доказательство того, что этих чисел бесконечно много, дал еще Евклид, живший в 300 г до н.э. Примерно в те же годы другой греческий математик, Эратосфен, придумал довольно-таки простой алгоритм получения простых чисел, суть которого была в последовательном вычеркивании чисел из таблицы. Те оставшиеся числа, которые ни на что не делились, и были простыми. Алгоритм называется «решето Эратосфена» и за счет своей простоты (в нем нет операций умножения или деления, только сложение) используется в компьютерной технике до сих пор. Видимо, уже во время Эратосфена стало ясно, что какого-либо четкого критерия, является ли число простым, не существует — это можно проверить лишь экспериментально. Существуют различные способы для упрощения процесса (например, очевидно, что число не должно быть четным), но простой алгоритм проверки не найден до сих пор, и скорее всего найден не будет: чтобы узнать, простое число или нет, надо попытаться разделить его на все меньшие числа.
Квадраты – «матрёшки»
Среди бесконечного множества квадратов, стороны которых выражены простыми числами, имеются пары квадратов, обладающие следующими свойствами:
квадрат с меньшей стороной вписывается в квадрат с большей стороной;
каждая вершина вписанного квадрата делит сторону описанного на два отрезка, которые выражаются целыми числами.
Такое вписывание одного квадрата в другой назовем целочисленным вписыванием.
Геометрический смысл этих свойств понятен из рисунка 1.

Рис. 1
Здесь каждый из четырех равных треугольников, образующихся при вписывании меньшего квадрата в больший, является основным пифагоровым треугольником, сумма катетов а + b которого равна стороне L описанного квадрата, а гипотенуза с — стороне l вписанного.
Основные пифагоровы треугольники (ОПТ) — это прямоугольные треугольники, стороны которых выражены тремя целыми числами, не имеющими общего делителя. Это, например, ОПТ со сторонами: 3, 4, 5; 5,12, 13; 15, 8, 17; 7, 24, 25; 21, 20, 29; 35, 12, 37 и др.
Значения сторон ОПТ определяются двойками натуральных чисел, обычно обозначаемых т и п (далее эти числа будем называть элементами т и п), которые удовлетворяют трем условиям: 1) т n; 2) т и п разночетны; 3) т и п взаимно просты, а формулы для нахождения сторон ОПТ через элементы т и п следующие:
нечетного катета: а = т2 – п2; четного катета: b = 2тп; гипотенузы: с = m2 + n2.
m = 2, n = 1 а = т2 – п2 = 22 – 12 = 4 – 1 = 3 b = 2тп = 2∙ 2 ∙1 = 4 L = a + b = 3 + 4 = 7 l = с = m2 + n2 = 22 + 12 = 4 + 1 = 5 | m = 6, n = 1 а = т2 – п2 = 62 – 12 = 36 – 1 = 35 b = 2тп = 2∙ 6 ∙1 = 12 L = a + b = 35 + 12 = 47 l=с = m2 + n2 = 62 + 12 = 36 + 1 = 37.
|
m = 6, n = 5
а = т2 – п2 = 62 – 52 = 36 – 25 = 11
b = 2тп = 2∙ 6 ∙5 = 60
L = a + b = 11 + 60 = 71
l = с = m2 + n2 = 62 + 52 = 36 + 25 = 61.
Пифагоровы тройки для m≤10
| m | n | a | b | c | m | n | a | b | c |
| 2 | 1 | 3 | 4 | 5 | 8 | 1 | 63 | 16 | 65 |
| 3 | 2 | 5 | 12 | 13 | 8 | 3 | 55 | 48 | 73 |
| 4 | 1 | 15 | 8 | 17 | 8 | 5 | 39 | 80 | 89 |
| 4 | 3 | 7 | 24 | 25 | 8 | 7 | 15 | 112 | 113 |
| 5 | 2 | 21 | 20 | 29 | 9 | 2 | 77 | 36 | 85 |
| 5 | 4 | 9 | 40 | 41 | 9 | 4 | 65 | 72 | 97 |
| 6 | 1 | 35 | 12 | 37 | 9 | 8 | 17 | 144 | 145 |
| 6 | 5 | 11 | 60 | 61 | 10 | 1 | 99 | 20 | 101 |
| 7 | 2 | 45 | 28 | 53 | 10 | 3 | 91 | 60 | 109 |
| 7 | 4 | 33 | 56 | 65 | 10 | 7 | 51 | 140 | 149 |
| 7 | 6 | 13 | 84 | 85 | 10 | 9 | 19 | 180 | 181 |
В качестве примеров пары квадратов с целочисленным вписыванием можно привести квадраты со сторонами 7 и 5, 47 и 37, 71 и 61.
Для большей наглядности эти примеры представим в виде следующей таблицы:
| m | n | L (a + b) | l (c) |
| 2 | 1 | 7 | 5 |
| 6 | 1 | 47 | 37 |
| 6 | 5 | 71 | 61 |
Какими же именно простыми числами должны быть выражены стороны двух квадратов, чтобы при вписывании меньшего из них в больший отрезки а и b выражались целыми числами?
Ответ на этот вопрос может быть найден при рассмотрении классификации простых чисел. Известно, что все простые числа, за исключением 1 и 2, подразделяются на четыре вида: 3 + 8k, 7 + 8k, 5 + 8k и 17 + 8k. (Приложение Таблица 1 и Таблица 2).
Как уже было сказано, при целочисленном вписывании квадрата со стороной l, выраженной простым числом, в квадрат со стороной L, также выраженной простым числом, имеет место равенство а2 +b2 = с2, где а + b = L, а с = l, причем а и b — целые числа. В сущности, это равенство представляет собой необходимое и достаточное условия целочисленного вписывания одного квадрата в другой. Остается выяснить, какого вида простыми числами должны быть выражены стороны меньшего и большего квадратов, чтобы эти условия выполнялись. Непосредственный опыт показывает, что если при целочисленном вписывании стороны и вписанного, и описанного квадратов выражены простыми числами, то таковыми для стороны вписанного квадрата являются только простые числа вида 5 + 8k и вида 17 + 8k, а для стороны описанного — только простые числа вида 7 + 8k или вида 17 + 8k. (Приложение Таблица 3)
Исходя из очевидных фактов, сформулируем следующие четыре утверждения, раскрывающие возможность и роль каждого вида простых чисел в целочисленном вписывании квадратов.
Если сторона квадрата выражена простым числом вида 3 + 8k, то невозможно ни вписать в него, ни описать вокруг него квадрат, представленный простым числом любого вида, чтобы при этом отрезки а и b (см. рисунок) выражались целыми числами.
Если сторона квадрата выражена простым числом вида 7 + 8k, то в него можно только вписать другой квадрат, и если сторона последнего представлена простым числом, то этим числом является простое число вида 5 + 8k или вида 17 + 8k.
Если сторона квадрата выражена простым числом вида 5 + 8k, то вокруг него можно только описать другой квадрат, и если сторона последнего представлена простым числом, то им является простое число вида 7 + 8k или вида 17 + 8k.
Если сторона квадрата выражена простым числом вида 17 + 8k, то в него можно вписать один квадрат и одновременно вокруг него можно описать также один квадрат, и если стороны последних представлены простыми числами, то ими для первого (вписанного) квадрата является простое число вида 5 + 8k или вида 17 + 8k, а для второго (описанного) — простое число вида 7 + 8k или вида 17 + 8k.
Четвертое утверждение делает возможным существование так называемых «квадратов-матрешек», которые подобно русской народной игрушке последовательно располагаются внутри друг друга, вписываясь в больший квадрат и одновременно описываясь вокруг меньшего. Первая такая «матрешка» из трех квадратов, стороны которых выражены только простыми числами, хорошо известна. Она состоит из квадрата со стороной 23 (простое число вида 7 + 8k), в который вписан квадрат со стороной 17 (простое число вида 17 + 8k), а этот последний описан вокруг квадрата со стороной 13 (простое число вида 5 + 8k). «Паспорт» этой трехквадратной «матрешки» выглядит следующим образом:
| т | п | L (a + b) | l с |
| 4 | 1 | 23 | 17 |
| 3 | 2 | 17 | 13 |
Здесь и далее жирным шрифтом обозначены простые числа вида 7 + 8k, курсивом – простые числа вида 17+8k, обычным шрифтом – простые числа вида 5 + 8k. Графическое изображение этой «матрешки» — на рисунке 2.
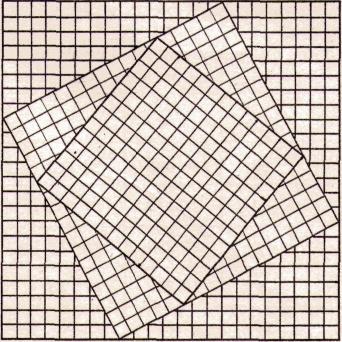
Рис. 2
Нужно сказать, что «матрешки» из трех квадратов со сторонами, выраженными простыми числами, встречаются довольно часто. Вот, например, еще две трехквадратные «матрешки», следующие сразу же за первой;
| т | п | L (a + b) | l с |
| 8 | 3 | 103 | 73 |
| 7 | 2 | 73 | 53 |
| 20 | 7 | 631 | 449 |
| 15 | 14 | 449 | 421 |
А возможны ли «матрешки» с большим числом квадратов, у которых стороны также выражены только простыми числами? Способность квадратов, стороны которых выражены простыми числами вида 17 + 8k, быть одновременно и вписанными, и описанными делает вероятным существование «матрешек», у которых между двумя крайними квадратами со сторонами, выраженными простыми числами вида 7 + 8k и вида 5 + 8k, располагаются не один, а несколько взаимно вписывающихся и описывающихся квадратов со сторонами, выраженными простыми числами вида 17 + 8k. И действительно, такие «матрешки» обнаружены. Таковы, например, первые четырехквадратные «матрешки», у которых по два промежуточных квадрата со сторонами, выраженными простыми числами вида 17 + 8k:
| т | п | L (a + b) | l с |
| 28 | 5 | 1039 | 809 |
| 25 | 4 | 809 | 641 |
| 19 | 10 | 641 | 461 |
| 28 | 25 | 1559 | 1409 |
| 27 | 20 | 1409 | 1129 |
| 25 | 14 | 1129 | 821 |
«Матрешки» из четырех и более квадратов, стороны которых выражены только простыми числами, встречаются, конечно, гораздо реже, чем трехквадратные. Например, «матрешка» из семи квадратов обнаружена пока в единственном экземпляре. Вот «паспортные» данные этого уникума (рис. 3):

Рис.3
| т | п | L (a + b) | l с |
| 92 | 35 | 13 679 | 9689 |
| 85 | 16 | 9689 | 7481 |
| 71 | 20 | 7481 | 5441 |
| 59 | 20 | 5441 | 3881 |
| 45 | 32 | 3881 | 3049 |
| 47 | 10 | 3049 | 2309 |
Следует заметить, что свойством быть одновременно и вписанными, и описанными обладают не только квадраты, стороны которых выражены простыми числами вида 17 + 8k, но и квадраты, стороны которых выражены составными числами, составленными только из простых чисел вида 17 + 8k. Поэтому имеются «матрешки», у которых стороны промежуточных квадратов — всех или некоторых — выражены произведением, степенью или произведением степеней простых чисел вида 17 + 8k.
В работе использовались таблицы распределения простых чисел по видам, составленные на основании таблиц простых чисел Д.Н. Лемера, а также таблицы основных пифагоровых треугольников, содержащие значения элементов т и п, сумм нечетного и четного катетов и гипотенуз . Комплекс вычислений выполнен в программе MS Excel.

Заключение
Пифагоровы тройки находят применение в проектировании множества вещей, окружающих нас в повседневной жизни. А умы учёных продолжают искать новые варианты использования простых чисел и пифагоровых троек. История того, что существуют числа, которые не делятся ни на какое другое число, люди знали еще в древности. Последовательность простых чисел имеет примерно следующий вид: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61 … Доказательство того, что этих чисел бесконечно много, дал еще Евклид, живший в 300 г до н.э. Примерно в те же годы другой греческий математик, Эратосфен, придумал довольно-таки простой алгоритм получения простых чисел, суть которого была в последовательном вычеркивании чисел из таблицы. Те оставшиеся числа, которые ни на что не делились, и были простыми. Алгоритм называется «решето Эратосфена» и за счет своей простоты (в нем нет операций умножения или деления, только сложение) используется в компьютерной технике до сих пор. Видимо, уже во время Эратосфена стало ясно, что какого-либо четкого критерия, является ли число простым, не существует — это можно проверить лишь экспериментально. В результате работы я расширила свои знания о пифагоровых тройках, убедилась в их уникальности. Узнала что существуют квадраты – «матрёшки» и научилась их построению.
Определение пифагоровых троек является как самостоятельной задачей, так и приложением к геометрическим задачам на теорему Пифагора. Используя приведенные в исследовании примеры, можно легко рассчитать различные комбинации. Числовой способ определения пифагоровых троек является самым простым с точки зрения понимания, но и самым трудоемким с точки зрения вычислений. В современных условиях при использовании компьютерных программ этот способ не представляет сложностей.
Полученные значения пифагоровых троек могут быть использованы при решении школьных задач по геометрии.
Литература
Атанасян, Л.С. Геометрия. 7-9 классы: учеб. для общеобразоват. организаций /Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.. - [5-е изд.]. – М.: Просвещение, 2015. - 383 с. |
Википедия. Общие сведения о Пифагоре. [Электронный ресурс]: свободная энциклопедия - режим доступа: ru.wikipedia.org/wiki/Пифагор. Приложения 1 сентября. Математика 2004 г |
Приложение 1
Доказательство формулы Евклида
Тот факт, что числа a, b, c, удовлетворяющие формуле Евклида, всегда составляют пифагоров треугольник, очевиден для положительных целых m и n, m n, поскольку после подстановки в формулы a, b и c будут положительными числами, а также из того, что выполняется равенство:
a2 + b2 = ( m2 – n2)2 + (2mn)2 = (m2 + n2)2 = c2.
Обратное утверждение, что a, b, c выражаются формулой Евклида для любой пифагоровой тройки, вытекает из следующего. Все такие тройки можно записать в виде (a, b, c), где a2 + b2 = c2 и a, b, c являются взаимно простыми, а b и c разночетны. (Если имеет ту же самую четность с обоими катетами, то в случае их четности они не будут взаимно простыми, а в случае нечетности a2 + b2 даст четное число, и оно не может быть равно нечетному c2.) Из a2 + b2 = c2 мы получаем c2 – a2 = b2, а следовательно, (c – a)(c + a) = b2 . Тогда  . Поскольку
. Поскольку  является рациональным, мы представим его в виде несократимой дроби
является рациональным, мы представим его в виде несократимой дроби  . Мы отсюда же получаем, что дробь
. Мы отсюда же получаем, что дробь  равна
равна . Решая уравнения
. Решая уравнения  относительно
относительно  получим
получим 
 . Поскольку
. Поскольку  несократимы по предположению, числители и знаменатели будут равными тогда и только тогда, правые части каждого неравенства несократимы. Как мы условились, дробь
несократимы по предположению, числители и знаменатели будут равными тогда и только тогда, правые части каждого неравенства несократимы. Как мы условились, дробь  тоже несократима, откуда следует, что m и n взаимно просты. Правые части будут несократимы тогда и только тогда, когда m и n имеют противоположную четность, так что числитель не делится на 2. А m и n должны иметь противоположную четность – оба не могут быть четными ввиду несократимости, а в случае нечетности обоих чисел деление
тоже несократима, откуда следует, что m и n взаимно просты. Правые части будут несократимы тогда и только тогда, когда m и n имеют противоположную четность, так что числитель не делится на 2. А m и n должны иметь противоположную четность – оба не могут быть четными ввиду несократимости, а в случае нечетности обоих чисел деление  на 2 даст дробь, в числителе и знаменателе которой будут нечетные числа, но эта дробь равна
на 2 даст дробь, в числителе и знаменателе которой будут нечетные числа, но эта дробь равна  , в которой числитель и знаменатель будут разночетны, что противоречит предположению. Теперь приравнивая числители и знаменатели, получим формулу Евклида a = m2 – n2, b = 2mn,
, в которой числитель и знаменатель будут разночетны, что противоречит предположению. Теперь приравнивая числители и знаменатели, получим формулу Евклида a = m2 – n2, b = 2mn,
c = m2 + n2 с m и n взаимно простыми и имеющими различную четность.
Более длинное, но и более общепринятое доказательство приведено в книгах Маора и Серпинского.
Таблица 1
| 3 + 8k | 5 + 8k | 7 + 8k | 17 + 8k |
| 3 | 5 | 7 | 17 |
| 11 | 13 | 23 | 41 |
| 19 | 29 | 31 | 73 |
| 43 | 37 | 71 | 89 |
| 59 | 53 | 79 | 97 |
| 67 | 61 | 103 | 113 |
| 83
| 101 | 127 | 137 |
| 107 | 109 | 151 | 193 |
| 139 | 149 | 167 | 233 |
| 163 | 157 | 191 | 241 |
| 179 | 173 | 199 | 257 |
| 211 | 181 | 223 | 281 |
| 227 | 197 | 239 | 313 |
| 251 | 229 | 263 | 337 |
| 283 | 269 | 271 | 353 |
| 307 | 277 | 311 | 401 |
| 331 | 293 | 359 | 409 |
| 347 | 317 | 367 | 433 |
| 379 | 341 | 383 | 449 |
| 419 | 349 | 431 | 457 |
| 443 | 373 | 439 | 521 |
| 467 | 389 | 463 | 569 |
| 491 | 397 | 479 | 577 |
| 499 | 421 | 487 | 593 |
| 523 | 461 | 503 | 601 |
| 547 | 509 | 599 | 617 |
| 563
| 541 | 607 | 673 |
| 571 57571 | 557 | 631 | 761 |
| 587 | 613
| 647 | 769 |
| 619 | 653 | 719 | 809 |
| 643 | 661 | 727 | 857 |
| 659 | 677 | 743 | 881 |
| 683 | 701 | 751 | 929 |
| 691 | 709 | 823 | 937 |
| 739 | 733 | 839 | 953 |
| 787 | 757 | 863 | 977 |
| 811 | 773 | 887 |
|
| 827 | 797 | 911 |
|
| 859 | 821 | 919 |
|
| 883 | 829 | 967 |
|
| 907 | 853 | 983 |
|
| 947 | 877 | 991 |
|
| 971 | 941 |
|
|
|
| 997 |
|
|
Таблица 2
Таблица простых чисел с остатками при делении на 8
| 2 | 2 | 233 | 1 | 547 | 3 | 877 | 5 |
| 3 | 2 | 239 | 7 | 557 | 5 | 881 | 1 |
| 5 | 5 | 241 | 1 | 563 | 3 | 883 | 3 |
| 7 | 7 | 251 | 3 | 569 | 1 | 887 | 7 |
| 11 | 3 | 257 | 1 | 571 | 3 | 907 | 3 |
| 13 | 5 | 263 | 7 | 577 | 1 | 911 | 7 |
| 17 | 1 | 269 | 5 | 587 | 3 | 919 | 7 |
| 19 | 3 | 271 | 7 | 593 | 1 | 929 | 1 |
| 23 | 7 | 277 | 5 | 599 | 7 | 937 | 1 |
| 29 | 5 | 281 | 1 | 601 | 1 | 941 | 5 |
| 31 | 7 | 283 | 3 | 607 | 7 | 947 | 3 |
| 37 | 5 | 293 | 5 | 613 | 5 | 953 | 1 |
| 41 | 1 | 307 | 3 | 617 | 1 | 967 | 7 |
| 43 | 3 | 311 | 7 | 619 | 3 | 971 | 3 |
| 47 | 7 | 313 | 1 | 631 | 7 | 977 | 1 |
| 53 | 5 | 317 | 5 | 641 | 5 | 983 | 7 |
| 59 | 3 | 331 | 3 | 643 | 3 | 991 | 7 |
| 61 | 5 | 337 | 1 | 647 | 7 | 997 | 5 |
| 67 | 3 | 347 | 3 | 653 | 5 |
|
|
| 71 | 7 | 349 | 5 | 659 | 3 |
|
|
| 73 | 1 | 353 | 1 | 661 | 5 |
|
|
| 79 | 7 | 359 | 7 | 673 | 1 |
|
|
| 83 | 3 | 367 | 7 | 677 | 5 |
|
|
| 89 | 1 | 373 | 5 | 683 | 3 |
|
|
| 97 | 1 | 379 | 3 | 691 | 3 |
|
|
| 101 | 5 | 383 | 7 | 701 | 5 |
|
|
| 103 | 7 | 389 | 5 | 709 | 5 |
|
|
| 107 | 3 | 397 | 5 | 719 | 7 |
|
|
| 109 | 5 | 401 | 1 | 727 | 7 |
|
|
| 113 | 1 | 409 | 1 | 733 | 5 |
|
|
| 127 | 7 | 419 | 3 | 739 | 3 |
|
|
| 31 | 7 | 421 | 5 | 743 | 7 |
|
|
| 137 | 1 | 431 | 7 | 751 | 7 |
|
|
| 139 | 3 | 433 | 1 | 757 | 5 |
|
|
| 149 | 5 | 439 | 7 | 761 | 1 |
|
|
| 151 | 7 | 443 | 3 | 769 | 1 |
|
|
| 157 | 5 | 449 | 1 | 773 | 5 |
|
|
| 163 | 3 | 457 | 1 | 787 | 3 |
|
|
| 167 | 7 | 461 | 5 | 797 | 5 |
|
|
| 173 | 5 | 463 | 7 | 809 | 1 |
|
|
| 179 | 3 | 467 | 3 | 811 | 3 |
|
|
| 181 | 5 | 479 | 7 | 821 | 5 |
|
|
| 191 | 7 | 487 | 7 | 823 | 7 |
|
|
| 193 | 1 | 491 | 3 | 827 | 3 |
|
|
| 197 | 5 | 499 | 3 | 829 | 5 |
|
|
| 199 | 7 | 503 | 7 | 839 | 7 |
|
|
| 211 | 3 | 509 | 5 | 853 | 5 |
|
|
| 223 | 7 | 521 | 1 | 857 | 1 |
|
|
| 227 | 3 | 523 | 3 | 859 | 3 |
|
|
| 229 | 5 | 541 | 5 | 863 | 7 |
|
|










 . Поскольку
. Поскольку  является рациональным, мы представим его в виде несократимой дроби
является рациональным, мы представим его в виде несократимой дроби  . Мы отсюда же получаем, что дробь
. Мы отсюда же получаем, что дробь  равна
равна . Решая уравнения
. Решая уравнения  относительно
относительно  получим
получим 
 . Поскольку
. Поскольку  на 2 даст дробь, в числителе и знаменателе которой будут нечетные числа, но эта дробь равна
на 2 даст дробь, в числителе и знаменателе которой будут нечетные числа, но эта дробь равна  , в которой числитель и знаменатель будут разночетны, что противоречит предположению. Теперь приравнивая числители и знаменатели, получим формулу Евклида a = m2 – n2, b = 2mn,
, в которой числитель и знаменатель будут разночетны, что противоречит предположению. Теперь приравнивая числители и знаменатели, получим формулу Евклида a = m2 – n2, b = 2mn, 









