Исследовательская работа "Я решаю уравнения: от сложного к простому" презентация 5 класс

Хоринский район

Муниципальное бюджетное общеобразовательное учреждение

«Санномыская средняя общеобразовательная школа»

Актуальность темы: Среди математических форм, таких как уравнение, задачи, неравенства и прочее - решение уравнений одна из проблемных в математике. В 5-м классе изучение уравнений начинается с определения уравнения, его корней, что значит решить уравнение. Чтобы решать более сложные уравнения, повторяются правила нахождения неизвестных компонентов сложения, вычитания, умножения, деления. Решаются уравнения, которые содержат буквенные выражения только в одной части уравнения. Для их решения учащиеся должны выполнить последовательно несколько преобразований, каждое из которых освоено ими в начальной школе. Однако, учащиеся 5 класса, затрудняются решать более сложные уравнения такого вида как (х + 111) - 38 =279 или 966 : (х + 17) = 23. Поэтому в своей работе я хочу показать, что процесс решения сложных уравнений можно осуществить через нестандартные способы решения и эти способы решения могут быть полезным и интересным занятием. В связи с этим, я считаю тему моей работы актуальной.

Гипотеза, цель, объект исследования, предмет исследования

Гипотеза: помогут ли мне в решении сложных уравнений изучение и применение нестандартных способов решения уравнений.

Цель: узнать нестандартные способы решения сложных уравнений и показать одноклассникам, что решать уравнения просто.

Объект исследования: сложные уравнения.

Предмет исследования: нестандартные способы решения сложных уравнений.

Задачи и методы исследования

ЗАДАЧИ:

1. Ознакомиться с информацией из разных источников по данной теме.

2. Изучить существующие нестандартные приёмы решения сложных уравнений

3. Поделиться опытом применения нестандартных способов решения сложных уравнений со своими сверстниками

Мероприятия:

- Анкетирование учащихся;

- Изучение и сбор нестандартных способов решения сложных уравнений для выявления более простого их решения

- ознакомление одноклассников с разными способами решения уравнения

МЕТОДЫ ИССЛЕДОВАНИЯ

1 . Тематический (изучение литературы из разных источников и в сети Интернет)

2. Эмпирический (организация и проведение анкетирования)

3. Статистический (обработка данных, полученных в ходе анкетирования)

:

1. Бекаревич А. Н. «Уравнения в школьном курсе математики» Минск. 1968 г., 99 стр.

2. Большая школьная энциклопедия 5 –11 классы – М.: ОЛМА-ПРЕСС, 2003.

3. Мерздяк А.Г. Математика: 5 класс: учебник/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир):. – М.: Вентана-Граф, 2019, 301 с.;.

4. Парканова, С. И., Линейные уравнения// С. И. Парканова, С. И. Ревтова, Т. М. Катлерова. Школьная педагогика. – 2016. – №2. – С. 19-22.

Сайт https://www.youtube.com/watch?v=ZRPlh6sFHbk

Сайт http://wiki.iteach.ru/index.php/История_возникновения_

уравнений

Отвечаем на вопросы – да или нет.

- Вы знаете, что такое уравнение?

- Вы знаете правило нахождения компонентов при сложении, вычитании, умножении, делении?

- Вы знаете, что значит решить уравнение?

- Вы знаете, что такое корень уравнения?

- Вы умеете решать уравнения?

и практической

х + 25 = 124; (х + 39) – 43 = 27;

х – 27 = 100; 253 – (х – 459) = 138;

19х = 95; (2х + 1) * 2 – 10 = 12

х + 25 = 124 (100%), (х + 39) – 43 = 27 ( 33%),

х – 27 = 100 (100%), 253 – (х – 459) = 138 (33%)

19х = 95 (56%), (2х + 1) * 2 – 10 = 12 (11%)

х : 25 = 16 (56%)

Вывод: Анкетирование показало, что более половины учащихся знают теоретический материал о решении уравнений. Практическая часть показала, что 44% учащихся не могут решать простые уравнения, из-за незнания правил работы с компонентами и 67% не могут решать более сложные уравнения.

После получения результатов анкетирования я решил изучить тематику линейных уравнений, выяснить какие способы решения линейных уравнений существуют, а затем ознакомить одноклассников с наработанным мною материалом и показать способы решения уравнений. Что и было сделано.

СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ

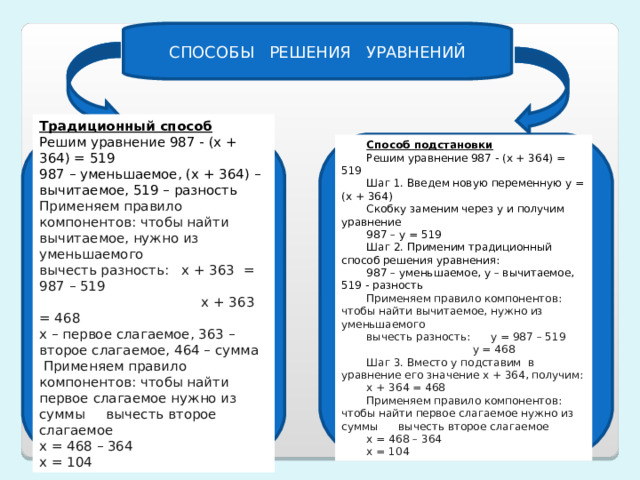
Традиционный способ

Решим уравнение 987 - (х + 364) = 519

987 – уменьшаемое, (х + 364) – вычитаемое, 519 – разность

Применяем правило компонентов: чтобы найти вычитаемое, нужно из уменьшаемого

вычесть разность: х + 363 = 987 – 519

х + 363 = 468

х – первое слагаемое, 363 – второе слагаемое, 464 – сумма

Применяем правило компонентов: чтобы найти первое слагаемое нужно из суммы вычесть второе слагаемое

х = 468 – 364

х = 104

Способ подстановки

Решим уравнение 987 - (х + 364) = 519

Шаг 1. Введем новую переменную у = (х + 364)

Скобку заменим через у и получим уравнение

987 – у = 519

Шаг 2. Применим традиционный способ решения уравнения:

987 – уменьшаемое, у – вычитаемое, 519 - разность

Применяем правило компонентов: чтобы найти вычитаемое, нужно из уменьшаемого

вычесть разность: у = 987 – 519

у = 468

Шаг 3. Вместо у подставим в уравнение его значение х + 364, получим:

х + 364 = 468

Применяем правило компонентов: чтобы найти первое слагаемое нужно из суммы вычесть второе слагаемое

х = 468 – 364

х = 104

987 - = 519

= 987 – 519

СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ

Решение уравнения по действиям

Рассмотрим линейное уравнение (2х + 1)*4 – 20 = 24.

Шаг 1: расставим порядок действий в левой части уравнения:

1)    Умножение в скобках;

2)    Сумма в скобках;

3)    Умножение за скобками;

4)    Вычитание.

Шаг 2: выполняем действия с конца уравнения, т.е. с четвертого по первое:

- (2х + 1)*4 – уменьшаемое;

- 20 – вычитаемое;

- 24 – разность.

Применяем правило компонентов: чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое:

(2х + 1)*4 = 44

Решаем полученное уравнение (2х + 1)*4 = 44

(2х + 1) = 44 : 4

(2х + 1) = 11

2х =11 – 1

2х = 10

Решаем полученное уравнение 2х = 10

х = 10 : 2

х = 5

Способ «закрывашка»

Покажем применение данного способа на том же уравнении

987 - (х + 364) = 519 закроем скобку «закрывашкой», получим уравнение

Х = 468 открываем «закрывашку» и получаем уравнение

х + 364 = 468

Применяем правило компонентов: чтобы найти первое слагаемое нужно из суммы вычесть второе слагаемое

х = 468 – 364

х = 104

СПОСОБЫ РЕШЕНИЯ УРАВНЕНИЙ

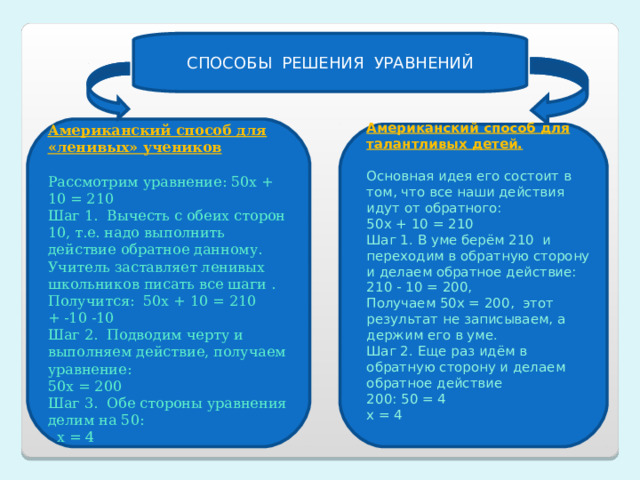
Американский способ для талантливых детей.  

Основная идея его состоит в том, что все наши действия идут от обратного:

50х + 10 = 210

Шаг 1. В уме берём 210 и переходим в обратную сторону и делаем обратное действие:

210 - 10 = 200,

Получаем 50х = 200, этот результат не записываем, а держим его в уме.

Шаг 2. Еще раз идём в обратную сторону и делаем обратное действие

200: 50 = 4

х = 4

Американский способ для «ленивых» учеников

Рассмотрим уравнение: 50х + 10 = 210

Шаг 1. Вычесть с обеих сторон 10, т.е. надо выполнить действие обратное данному. Учитель заставляет ленивых школьников писать все шаги .

Получится: 50х + 10 = 210

+ -10 -10

Шаг 2. Подводим черту и выполняем действие, получаем уравнение:

50х = 200

Шаг 3. Обе стороны уравнения делим на 50:

х = 4

Вывод: Изучив литературу и интернет ресурсы по данной тематике, я убедился в том, что линейные уравнение имеют большое практическое значение.

Из всех способов решения линейного уравнения, я выбираю традиционный, т к он является классическим, хотя для простоты решения могу рекомендовать способ «закрывашка».

Как видите, эта идея решения линейных уравнений очень проста.

РЕЗУЛЬТАТЫ ПОВТОРНОГО АНКЕТИРОВАНИЯ

х + 25 = 124 (100%), х – 27 = 100 (100%)

19х = 95 (100%) х : 25 = 16 (100%)

(х + 39) – 43 = 27 ( 77%), 253 – (х – 459) = 138 (77%)

(2х + 1) * 2 – 10 = 12 (44%)

На вопрос «Какой способ при решении уравнений вами выбран и почему?»

Традиционный способ (33%), т к он классический

«Закрывашка» (77%) наиболее простой

Вывод: считаю, что моя гипотеза «помогут ли мне в решении сложных уравнений рассмотрение и применение нестандартных способов решения уравнений» подтвердилась, поставленную перед собой цель и задачи я выполнил. Так же я сумел убедить своих одноклассников в том, что решать уравнения легко и просто, если ты владеешь разными способами решения уравнений .

ЗАКЛЮЧЕНИЕ:

Изучив литературу и интернет ресурсы по данной тематике, я убедился в том, что линейные уравнение имеют большое практическое значение как в математике, так и в физике, информатике, химии. Изучил и познакомился с разными способами решения линейного уравнения с одной переменной: традиционным, способ «закрывашка», подстановка, решение по действиям, американский способ для «ленивых» учеников, американский способ для талантливых детей. 

Из всех способов решения линейного уравнения, я выбирал традиционный, т к он является классическим, хотя для простоты решения могу рекомендовать способ «закрывашка», позволяющий легко и просто решать сложное уравнения с одной переменной. Однако нужно отметить, что каждый способ решения уравнений по-своему уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на контрольных работах и ВПР.

Считаю, что моя гипотеза «помогут ли мне в решении сложных уравнений рассмотрение и применение нестандартных способов решения уравнений» подтвердилась, поставленную перед собой цель и задачи я выполнил. Так же я сумел убедить своих одноклассников в том, что решать уравнения легко и просто, если ты владеешь разными способами решения уравнений.

Спасибо за внимание.

исполнитель: Скрипин Дмитрий ученик

5 – го класса.

руководитель: Романова Евгения

Ильинична

должность: учитель физики и математики

место работы: МБОУ «Санномыская СОШ»