Исследовательская работа "Изучение свойств листа Мёбиуса."

Муниципальное автономное образовательное учреждение «Траектория»

Учебно-исследовательская конференция учащихся

Секция: естественнонаучная

Тема: «Лист Мёбиуса»

Автор: Новикова Софья,

ученица 5 «А» класса

Руководитель:

МедведеваЛ.В.,

учитель математики

г. Пермь, 2018 г.

Содержание

• Введение 3-4

• Историческая справка 5

• Топология – «геометрия положения» 6-7

• Изготовление модели листа Мёбиуса 8

• Свойства листа Мёбиуса 9-10

• Сюрпризы листа Мёбиуса 11-13

• Лист Мёбиуса в искусстве 14-15

• Применение листа Мёбиуса 16

• Объекты, подобные листу Мёбиуса 17-18

• Заключение 19

• Список использованной литературы 20

Введение

Лист Мебиуса - символ математики,
Что служит высшей мудрости венцом…
Он полон неосознанной романтики:
В нем бесконечность свернута кольцом.

В нем – простота, и вместе с нею – сложность,

Что недоступна даже мудрецам:
Здесь на глазах преобразилась плоскость
В поверхность без начала и конца.

Здесь нет пределов, нет ограничений,
Стремись вперед и открывай миры,
Почувствуй силу новых ощущений,
Прими познанья высшего дары:

Познай любовь и ненависть изведай,
Низвергнись в ад – тотчас увидишь рай.
Ты в одночасье насладись победой
И горечь пораженья испытай.

На грани бесконечного блаженства
Испытывая суеверный страх,
Найдешь свой путь. Достигнув совершенства,
Окажешься в таинственных мирах.

И, вдохновленный этим дерзновеньем,
По экспоненте поднимаясь в высь,
Ты ощутишь восторг освобожденья,
Почувствуешь, как возникает Мысль.

Покажется, что распростерлась Вечность,
Что взломан Мироздания пароль.
И вдруг твое стремленье в бесконечность
Тебя вернет к исходной точке: в ноль.

Как о порог, об этот ноль споткнешься.
Но как бы ни был прежний путь тернист,
Вновь выбирай (и ты не ошибешься!)
Путь в бесконечность – Мёбиуса лист!

На одном из занятий факультатива «Занимательная математика» мы проводили эксперименты над удивительной поверхностью – листом Мёбиуса. Своё название лист Мёбиуса получил по имени немецкого геометра и астронома Августа Фердинанда Мёбиуса, который впервые получил эту поверхность и изучил её свойства. Результаты проведённых на факультативе экспериментов меня заинтересовали. Дома я продолжила опыты с таинственным листом Мёбиуса и сделала для себя маленькие открытия, которые отражены в данной работе.

Цель работы: изучение свойств листа Мёбиуса.

Задачи: 1. Познакомиться с биографией Августа Фердинанда Мёбиуса.

2. Познакомиться с понятием «топология».

3. Провести ряд экспериментов над листом Мёбиуса.

4. Собрать материл о применении листа Мёбиуса в искусстве.

Историческая справка

Август Фердинанд Мёбиус – немецкий

математик и астроном-теоретик – родился

в 1790 году в Шульпфорте. Его отец был

учителем танцев в княжеской школе

Шульпфорта. Мать Мёбиуса была потомком

Мартина Лютера.

В 1813 - 1814 годах Мёбиус был учеником

«короля математиков» Карла Гаусса.

Мёбиус был первоначально астрономом, как

сам Гаусс и многие другие из тех, кому

математика обязана своим развитием. В те

времена изучение математики не встречало

17.11.1790 - 26.09.1868 поддержки, а занятие астрономией давало

достаточно денег, чтобы не думать о них, и оставляло время для размышлений. С 1816 года Мёбиус начал вести самостоятельные астрономические наблюдения в Плейсенбургской обсерватории, в 1818 году стал её директором, а позже - профессором математики Лейпцигского университета.

А.Ф.Мёбиус сделал много интересных открытий, стал одним из крупнейших геометров XIX века. Он – один из основоположников теории геометрических преобразований, теории векторов и многомерной геометрии. Важные результаты были получены им и в теории чисел (функция Мёбиуса).

Мёбиус впервые ввёл систему координат и аналитические методы исследования, установил существование многогранников, для которых не применим «закон рёбер» и которые не имеют объёма. Мёбиус открыл ряд теорем, «предметом которых служат по большей части метрические отношения, но такие, которые зависят не от отношений величин и углов фигур, а исключительно от начертательных отношений построения, то есть относящихся только к положению (проективные)». Именно Мёбиусу принадлежит идея выражать один и тот же отрезок, проходимый в противоположных направлениях, через АВ и ВА, полагая, что АВ = - ВА. Эта достаточно очевидная в наше время идея позволила впервые научно обосновать тригонометрию и векторные методы в математике.

В возрасте 68 лет Мёбиусу удалось сделать открытие поразительной красоты. Он открыл односторонние поверхности, одна из которых – лист Мёбиуса. Эта поверхность является объектом топологии - области математики, одним из основателей которой по праву считается Мёбиус.

Топология – «геометрия положения»

Топология (от греческого topos – место и logos – слово, учение) – раздел математики, изучающий топологические свойства фигур, то есть свойства, не изменяющиеся при топологических преобразованиях (непрерывных деформациях, растяжениях и сжатиях без разрывов).

Фигуры, получающиеся одна из другой с помощью топологических преобразований, называются топологически эквивалентными (гомеоморфными). У таких фигур топологические преобразования искажают форму, изменяют размеры, нарушают прямолинейность сторон и величины углов, но у них у всех сохраняются общие топологические свойства.

Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать – делать с ней всё, что угодно, только не разрывать и не склеивать. И при этом будет считаться, что ничего не произошло, все свойства остались неизменными.

Например, окружность, эллипс и контур квадрата имеют одни и те же топологические свойства. Значит, эти линии могут быть деформированы одна в другую. Следовательно, они являются гомеоморфными.

В то же время кольцо и круг обладают различными топологическими свойствами: круг ограничен одним контуром, а кольцо – двумя. Значит, эти фигуры гомеоморфными не являются.

Другой пример. С точки зрения топологии баранка и кружка – это одно и то же. Сжимая и растягивая кусочек резины, из которой изготовлены эти тела, можно перейти от одного тела к другому. А вот баранка и шар – разные объекты, так как чтобы сделать отверстие, надо разорвать резину.

Какие топологические свойства должны быть у фигур?

• Непрерывность: после деформации фигуры её соседние точки должны оставаться соседними.

С топологической точки зрения круг не отличим от квадрата или треугольника, потому что их легко преобразовать один в другой, не нарушая непрерывности.

• Связность: число сквозных (от края до края) разрезов, которое выдерживает фигура, не распадаясь при этом на части. Если любой разрез разбивает плоскость на две части, то она называется односвязной, то есть состоит из одного куска. Если же поверхность распадается после двух разрезов, то это двусвязная поверхность.

Чтобы разделить квадрат на две части, достаточно сделать один разрез от стороны к стороне. А для разделения кольца на две части необходимы два разреза. По мнению топологов квадрат и ромашка – односвязны, кольцо и оправа для очков – двусвязны, решётки и диски с отверстиями – многосвязны.

• Количество сторон

У бумажного кольца две стороны. Но если перед склеиванием один из концов бумажной полоски повернуть на 180°, то полученное кольцо будет иметь только одну сторону.

• Количество краёв

Обычный лист бумаги – двусторонняя односвязная поверхность с одним краем. Его можно смять и бросить в урну, но всё равно число краёв и сторон останется прежним. А у сферы и у тора (бублика) нет краёв. Зато нарисованное на бумаге кольцо имеет два края.

• Ориентированность: ориентируемая поверхность – поверхность, допускающая ориентацию (определение своего местоположения). Ориентируемые поверхности имеют две стороны в отличие от не ориентируемых односторонних поверхностей.

• Хроматический номер: максимальное число областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими. Если каждую такую область покрасить в разные цвета, то любой цвет должен соседствовать с любым другим. На листе бумаги, даже если его склеить в кольцо, можно расположить не более четырёх цветных пятен любой формы, которые имели бы всеобщую границу. На сфере и на цилиндре их также может быть не более четырёх. Значит, хроматический номер этих поверхностей равен четыре. На бублике число цветов может быть равно семи, то есть его хроматический номер – семь.

Топологические свойства фигур связаны с наиболее абстрактными математическими дисциплинами – алгеброй и теорией функций. Понятия и теоремы топологии полезны и в других областях математики, в технике, экономике, психологии.

Одним из объектов топологии является лист Мёбиуса. Именно открытие этой удивительной поверхности, свойства которой приводили в восхищение многих людей, прямо или косвенно связанных с математикой, положило начало развитию новой ветви геометрии – топологии.

Изготовление модели листа Мёбиуса

В 1868 году немецким геометром и астрономом Августом Фердинандом Мёбиусом была открыта необычная поверхность. Примерно в это же время независимо от Мёбиуса эта же поверхность была рассмотрена ещё одним немецким математиком, профессором Геттингенского университета Иоганном Бенедиктом Листингом. Однако историки-математики закрепили за ней имя Мёбиуса. Новое открытие получило название – лист Мёбиуса.

Существует легенда, по которой внимание Мёбиуса привлекла перекрученная лента, которую неправильно соединила его служанка, что и подтолкнуло великого математика к изучению свойств полученной поверхности.

Для изготовления модели листа Мёбиуса необходимо вырезать из бумаги прямоугольную полоску АВВ'А'.

Затем полоску надо перекрутить на 180° и склеить противоположные стороны АВ и А'В' так, чтобы точка А совместилась с точкой В', а точка В совместилась с точкой А'.

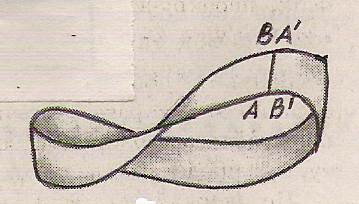
В результате получится знаменитое в математике бумажное кольцо, называемое листом Мёбиуса.

Полоска для ленты Мёбиуса должна быть длинной и узкой, причём, чем длиннее полоска, тем легче склеить лист Мёбиуса. Видимо, должно существовать такое число Х, что из полоски, у которой длина больше Х, лист Мёбиуса можно склеить, а из полоски меньшей длины – нельзя. Значение такого числа до сих пор не найдено, лишь известно, что оно должно удовлетворять неравенству π/2 ≤ Х ≤ √ 3.

Свойства листа Мёбиуса

Лист Мёбиуса наделён удивительными свойствами, которые не связаны с его положением в пространстве, с понятиями расстояния и угла. Тем не менее эти свойства имеют вполне геометрический характер. Их изучением занимается топология.

• Сколько сторон у листа Мёбиуса?

Лента, из которой сделан лист Мёбиуса, имеет две стороны. А у него самого, оказывается, только одна сторона!

Это подтверждается следующими опытами:

• У не перекрученного бумажного кольца две стороны: внешняя и внутренняя. Если раскрашивать внешнюю сторону этого кольца, то, не пересекая «границы», нельзя очутиться на другой его стороне, то есть внутри кольца. А если раскрашивать лист Мёбиуса, не переходя за его край, то лист закрасится весь!

Рихард Курант и Герберт Робинс в своей книге «Что такое математика» пишут: «Если кто-нибудь вздумает раскрасить только одну сторону поверхности мёбиусовой ленты, пусть лучше сразу погрузит её всю в ведро с краской».

• Если на внутреннюю сторону обычного кольца посадить паука, а на наружную – муху и разрешить им ползать как угодно, запретив лишь перелезать через края кольца, то паук не сможет добраться до мухи. А если их обоих посадить на лист Мёбиуса, то бедная муха будет съедена.

• Если двигать какой-нибудь объект вдоль листа Мёбиуса, то он вернётся в исходное место, оказавшись в перевёрнутом положении по сравнению с первоначальным. А чтобы этот объект вернулся к месту старта в нормальном положении, ему нужно совершить ещё одно «круголистное» путешествие.

Итак, обычное бумажное кольцо является двусторонней поверхностью, а лист Мёбиуса представляет собой одностороннюю поверхность. Эти две фигуры имеют различные топологические свойства. Значит, они не являются гомеоморфными. Следовательно, невозможно получить первую поверхность из второй и наоборот.

• К ак на листе Мёбиуса расположена его средняя линия?

У листа Мёбиуса только одна сторона. Поэтому и средняя линия на нём также расположена односторонне.

• Можно ли найти на листе Мёбиуса замкнутую кривую, которая разбила бы его на две части?

Если на листе Мёбиуса вырезать дыру, то границами этой дыры будет замкнутая кривая (например, окружность или квадрат). А вырезанный кусочек и сам лист Мёбиуса без этого кусочка будут являться теми двумя частями, на которые замкнутая кривая разбила лист Мёбиуса. Следует заметить, что разрез не по всякой замкнутой кривой на листе Мёбиуса разбивает его на две части. Например, разрез по средней линии этого не делает.

• Сколько надо сделать разрезов, чтобы лист Мёбиуса распался на две части?

Любых два разреза разбивают лист Мёбиуса на части. Если разрезать его вдоль, он превратится в одну целую ленту. Поэтому лист Мёбиуса – двусвязная поверхность. Если перед разрезанием перекрутить ленту на два оборота, то лист становится односвязным. При трёх оборотах связность снова равна двум.

• Лист Мёбиуса непрерывен, так как любая его точка может быть соединена с любой другой точкой.

• У листа Мёбиуса один край, как и одна сторона.

• Ориентированность у листа Мёбиуса отсутствует. Представим, что внутри этого листа заключён целый плоский мир, где есть только два измерения, а его обитатели – несимметричные рожицы, не имеющие, как и сам лист никакой толщины. Если эти создания пропутешествуют по всем изгибам листа Мёбиуса и вернутся в родные пенаты, то в изумлении обнаружат, что превратились в своё собственное зеркальное отображение.

• Хроматический номер листа Мёбиуса равен шести.

• Существуют два типа полос Мёбиуса в зависимости от направления закручивания: правые и левые. Поэтому лист Мёбиуса хирален.

• Бесконечно широкий и не пересекающий сам себя лист Мёбиуса не помещается в трёхмерное пространство. Он может существовать только в четырёхмерном пространстве.

С 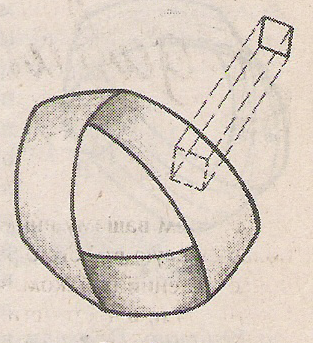юрпризы листа Мёбиуса

Эксперимент 1. Разрезать лист Мёбиуса по средней линии.

• Е сли такой эксперимент провести с обычным кольцом, то оно распадётся на два узких кольца. А лист Мёбиуса в этом случае не распадётся на две части, а превратится в замкнутую, перекрученную на 360° ленту, причём в два раза длиннее и в два раза уже исходной. Объяснение этого факта вытекает из свойств односторонних поверхностей, при перемещении вдоль которых направление изменяется на противоположное в момент возвращения в исходную точку.

Эксперимент 2. Разрезать по середине кольцо, полученное в предыдущем эксперименте.

• В результате разрезания получаются два сцепленных друг с другом кольца, каждое из которых дважды перекручено.

Эксперимент 3. Разрезать лист Мёбиуса по средней линии, перекрутив его перед склеиванием три раза.

• Получится лента, завитая в узел трилистника.

Разрез листа Мёбиуса с дополнительными перекручиваниями даёт неожиданные фигуры, названные парадромными кольцами.

Эксперимент 4.

Трилистник

Разделить ленту по ширине двумя пунктирными линиями на три одинаковых части. Склеить лист

М ёбиуса и разрезать его по пунктиру.

• Е сли бы лента не была перекручена, то сначала бы отрезалось одно кольцо, а потом разделились бы два остальных. Всего получилось бы три кольца той же длины, что и первоначальное, но по ширине в три раза меньше.

Но так как из ленты склеен лист Мёбиуса, то эта лента разрежется по всем пунктирным линиям сразу, «не отрывая» ножниц от бумаги. В результате получится два сцепленных кольца. Одно из них вдвое длиннее первоначальной ленты и перекручено два раза. Оно получилось из краёв исходной ленты. Второе кольцо представляет из себя новый лист Мёбиуса, который состоит из центральной части исходного листа Мёбиуса. Поэтому его ширина в три раза меньше, чем у исходного.

Эксперимент 5. Взять сцепленные между собой кольца из предыдущего эксперимента. Раскрасить маленький лист Мёбиуса краской и уложить с обеих сторон от него второе кольцо, то есть проделать задание, обратное предыдущему.

• Получится интересная фигура, у которой две крайние не закрашенные части, сделанные из одного кольца, нигде не имеют общих точек, а лежат вдоль сторон третьей закрашенной части. Так как средняя часть представляет собой лист Мёбиуса, то крайние части тоже представляют собой «два листа Мёбиуса, которые обрели самостоятельность, обвившись вокруг цветного листа Мёбиуса».

Э ксперимент 6. Разделить ленту по ширине тремя пунктирными линиями на четыре одинаковых части. Склеить лист Мёбиуса и разрезать его по пунктиру.

• В этом случае придётся делать два разреза, в результате которых получатся два сцепленных друг с другом кольца в два раза большие по длине и в четыре раза меньшие по ширине по сравнению с данным кольцом.

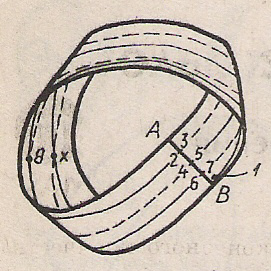
Эксперимент 7. Склеить лист Мёбиуса, предварительно разделив его по ширине на четыре равные части. Провести на нём прямую линию, начинающуюся от края листа Мёбиуса с цифры 1 и соединяющую поочерёдно все точки от 1 до 8. (Пунктиром на рисунке обозначена часть линии, оказавшаяся с внутренней стороны листа).

Разрезать получившийся лист Мёбиуса.

• Проведя все необходимые операции и оказавшись в точке 8, лист Мёбиуса распадается на две части. Но, прежде в точке Х произойдёт его самопересечение и он раскроется. Поэтому возникает впечатление того, что разрез не представляет собой непрерывную прямую, хотя проведённая перед разрезанием прямая линия была непрерывной. Итак, в результате разрезания получились две длинные полоски, причём равной площади.

Д 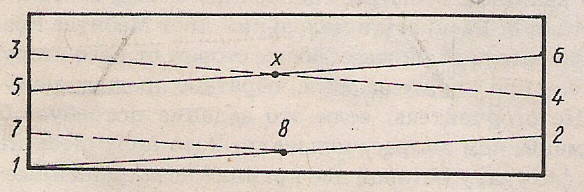ля доказательства этого факта необходимо разрезать аналогичный данному лист Мёбиуса перпендикулярно средней линии от края до края по отрезку АВ. Затем поочерёдно соединить точки в том порядке, в каком производился разрез на листе Мёбиуса. В результате получится модель листа Мёбиуса, для которого проводится доказательство.

Н 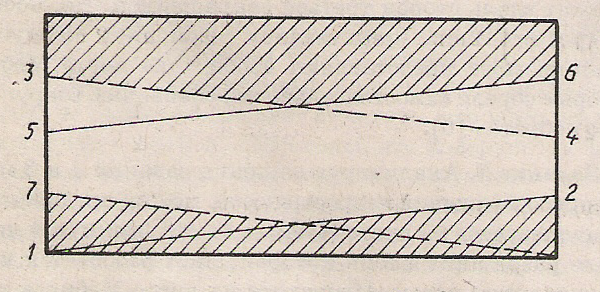а данном рисунке заштрихована одна из получившихся в результате разрезания полосок. Если совместить верхнюю и нижнюю части заштрихованной области, то можно заметить, что площади заштрихованной и не заштрихованной частей равны. Следовательно, при подобном разрезании листа Мёбиуса получаются две полоски равной площади.

Э ксперимент 8. Разделить ленту по ширине четырьмя пунктирными линиями на пять одинаковых частей. Склеить лист Мёбиуса и разрезать его по пунктиру.

• В данном случае получится три кольца. Одно кольцо по длине, равной длине исходного кольца, а ширине в пять раз меньшей его, будет представлять собой лист Мёбиуса. Два других кольца будут дважды перекручены, по длине в два раза больше, а по ширине в пять раз меньше исходного кольца. Они окажутся сцеплены между собой и сцеплены с первым кольцом.

Лист Мёбиуса в искусстве

Лист Мёбиуса служил вдохновением для скульптур и графического искусства.

Голландский график XIX века Мауриц Эшер был одним из тех, кто особенно любил этот математический объект. Он посвятил этой удивительной поверхности несколько своих литографий. Одна из известных гравюр «Лист Мёбиуса II» показывает муравьёв, ползающих по поверхности этого удивительного листа.

Серию вариантов листа Мёбиуса создал скульптор XX века Макс Билл. В течение почти 20 лет он неоднократно обращался к листу Мёбиуса, стремясь выразить в скульптуре идею вечного движения и развёртывающейся в пространстве формы. Его скульптура «Узел без конца» находится в национальном музее современного искусства в Париже.

С изучением свойств листа Мёбиуса началось развитие новой ветви геометрии – топологии, которая сыграла исключительную роль в развитии науки в целом. Именно поэтому в Вашингтоне у входа в Музей истории и техники установлен монумент этой поверхности, высотой более двух метров. Он представляет собой медленно вращающуюся на пьедестале стальную ленту, закрученную на полвитка.

В 1967 году, когда в Бразилии состоялся международный математический конгресс, его устроители выпустили памятную марку достоинством в пять сентаво. На ней была изображена лента Мёбиуса.

Лист Мёбиуса также постоянно встречается в художественной литературе.

В научно-фантастическом рассказе Артура Кларка «Стена темноты» предполагается, что наша Вселенная может быть некоторым обобщённым листом Мёбиуса.

В рассказе А. Дж. Дейча «Лист Мёбиуса» бостонское метро строит новую линию, маршрут которой становится настолько запутанным, что превращается в ленту Мёбиуса, после чего на этой линии начинают исчезать поезда.

В романе коста-риканского писателя Хоакина Гутьерреса «Умрём, Федерико?» даётся описание листа Мёбиуса: «Сегодня учительница показала нам ленту Мёбиуса. Вот здорово! Возьмёшь бумажную полоску – лучше от газеты, чтобы была длиннее, и увидишь, что полоска имеет две стороны; подтверждение этому – если муравей захочет поползать по одной стороне, он может сколько угодно делать это, но чтобы попасть на другую сторону, он должен обязательно перелезть через кромку. Поэтому и говорят, что полоса имеет две стороны. А вот лента Мёбиуса получается так. Надо перевернуть один конец полосы, словно собираешься её закручивать, но делаешь всего один поворот и склеиваешь концы. Тогда бумага будет иметь только одну сторону, и любой, кто хочет, может проверить, если сомневается. Ведя пальцем, будто преследуешь муравья по всей ленте, вдруг убеждаешься в том, что обе стороны сошлись в одну и не надо пересекать кромку».

Ещё более романтически описывает лист Мёбиуса Эдуард Успенский в своей повести «Красная рука, чёрная простыня, зелёные пальцы»:

«… Но больше всего поразил Рахманина какой-то старинный то ли знак, то ли вензель, то ли орден очень и очень аккуратной работы. Никогда раньше он не видел ничего похожего. Это изделие напоминало или старинный герб иностранного дворянского рода, или герб страховой компании, торгующей научными приборами, потому что основу его составляла лента Мёбиуса. Эта вещь очень понравилась Рахманину… В знаке совершенно чётко проступал какой-то смысл, были заложены определённые пропорции и связи… Вещь была красивая, просто музейная ».

Применение листа Мёбиуса

Лист Мёбиуса находит многочисленные применения в науке, технике, изучении свойств Вселенной.

Устройство под названием «резистор Мёбиуса» - это недавно изобретённый электронный элемент, который не имеет собственной индуктивности. Американский изобретатель в области электро- и радиотехники Никола Тесла запатентовал подобное устройство в начале 1900-х годов. Катушка для электромагнитов предназначалась для использования в его системе глобальной передачи электричества без проводов.

Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему дольше работать, так как в этом случае поверхность ленты изнашивается в два раза медленнее. Это даёт ощутимую экономию.

Исследователи из университета японского города Хоккайдо создали кристаллические структуры, имеющие одну поверхность, наподобие листа Мёбиуса. Эти структуры представляют собой единые кристаллы без швов и других дефектов. Тонкие кристаллические ленты из селенида ниобия синтезировались путём нагревания селена и ниобия в герметической кварцевой трубке. Японские учёные усовершенствовали обычную методику синтеза кристаллов, создав градиент температуры, благодаря чему селен мог присутствовать в трубке одновременно в газообразной и жидкой фазе. Поверхностное натяжение жидкости способствовало образованию замкнутых колец различной конфигурации, среди которых были и листы Мёбиуса. Необычные кристаллы могут найти применение в исследовании топологических эффектов в квантовой механике.

Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мёбиуса и только поэтому генетический код так сложен для расшифровки и восприятия. Более того, такая структура вполне логично объясняет причину наступления биологической смерти – спираль замыкается сама на себя и происходит самоуничтожение или аннигиляция, как подтверждают физики. По их мнению все оптические законы основаны на свойствах ленты Мёбиуса, в частности отражение в зеркале – это своеобразный перенос во времени, краткосрочный, длящийся сотые доли секунды, ведь мы видим перед собой зеркального двойника.

Лист Мёбиуса применяется в магнитофонах, в которых лента имеет такую же одностороннюю поверхность. В результате этого удваивается время непрерывного звучания. Существуют и принтеры, в которых бумажная лента склеена листом Мёбиуса. Так же лист Мёбиуса используется в фильтрах, в детских игрушках и даже в цирке.

Объекты, подобные листу Мёбиуса

В 1882 году немецкий математик Феликс Клейн построил ещё одну одностороннюю поверхность, но уже замкнутую, которую в честь него назвали бутылкой Клейна.

Неизвестный автор посвятил этому шуточное стихотворение:

Великий Феликс,

Славный Клейн,

Мудрец из Геттингема

Считал, что Мёбиуса лист –

Дар свыше несравненный.

Гуляя как- то раз в саду,

Воскликнул Клейн наш пылко:

«Задача проста-

Возьмём два листа

И склеим из них бутылку!»

Из последних строчек стихотворения понятно, что бутылка Клейна может быть получена путём склеивания двух лент Мёбиуса по краям.

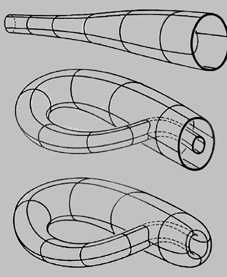Но её можно сделать и из обычной бутылки с абсолютно тонкими стенками. Для этого нужно вытянуть горлышко обычной бутылки, опустить вниз и проткнуть стенку. Горлышко тянуть до пересечения с другой стенкой или дном и вывести наружу так, чтобы края горлышка были вровень с пересекаемой поверхностью. Теперь на поверхности бутылки можно провести линию, которая будет проходить и внутри, и снаружи бутылки, не пересекая края бутылки, то есть по одной поверхности.

Обычная бутылка имеет наружную и внутреннюю стороны. Если муха захочет переползти с наружной поверхности на внутреннюю или наоборот, ей обязательно придётся пересечь край, образуемый горлышком. А бутылка Клейна не имеет края, её поверхность нельзя разделить на внутреннюю и наружную. Та поверхность, которая кажется наружной, непрерывно переходит в ту, которая кажется внутренней, как переходят друг в друга, на первый взгляд различные «стороны» листа Мёбиуса.

В обычном трёхмерном евклидовом пространстве нельзя построить бутылку Клейна, поверхность которой была бы свободна от точек самопересечения.

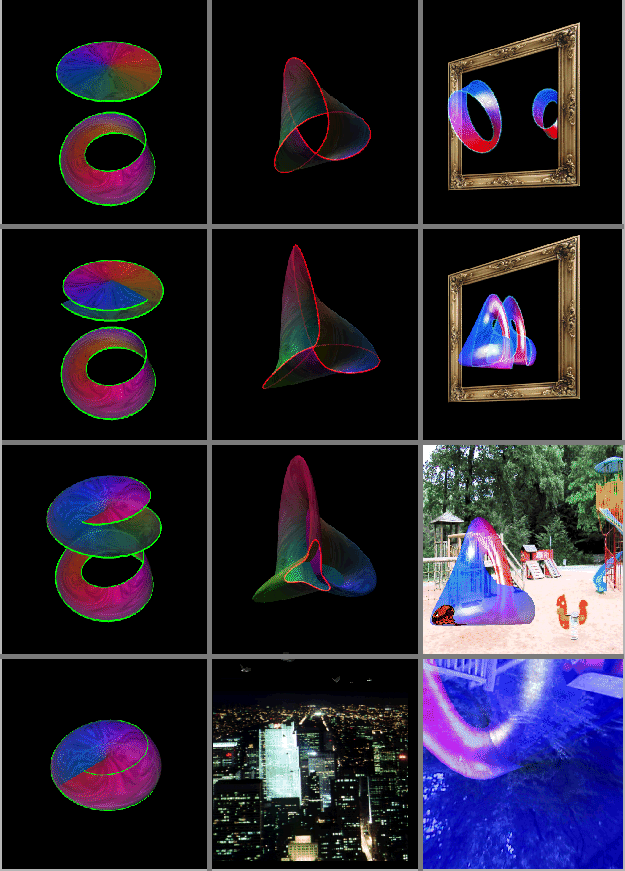
Есть ещё один похожий на лист Мёбиуса геометрический объект – вещественная проективная плоскость. Если проколоть отверстие в вещественной проективной плоскости, тогда то, что останется будет листом Мёбиуса. С другой стороны, если приклеить диск к ленте Мёбиуса, совмещая их границы, то результатом будет проективная плоскость. Чтобы визуализировать это, полезно деформировать ленту Мёбиуса так, чтобы её граница стала обычным кругом. Такую фигуру называют «пересечённая крышка».

Заключение

Физики-теоретики пришли к выводу, что наша Вселенная, вполне вероятно, замкнута в ленту Мёбиуса. Эта теория полностью взаимосвязана с теорией относительности Энштейна и его предположением, что космический корабль, всё время летящий прямо, может вернуться к месту старта, что подтверждает неограниченность и конечность Вселенной, изогнутой в пространстве большого числа измерений. По теории относительности чем больше масса, тем больше кривизна пространства. Оппоненты этой теории утверждают, что для искривления Вселенной как у листа Мёбиуса не хватит массы. Но, во-первых, распределение плотности вещества ещё до конца не изучено, во вторых, не учитывается наличие так называемой «скрытой массы», да и нейтрино, как выяснилось совсем недавно, обладают положительной массой покоя, а не нейтральны. Всё это научные гипотезы, а на практике описанная в 1865 году профессором Лейпцигского университета Августом Фердинандом Мёбиусом лента, благодаря стараниям изобретателей и её удивительным свойствам, стала неисчерпаемым источником оригинальных технических решений.

Лист Мёбиуса иногда называют прародителем символа бесконечности ( ∞ ), так как находясь на поверхности ленты Мёбиуса, можно было бы идти по ней вечно. На самом деле это не соответствует действительности, так как символ бесконечности использовался в течение двух столетий до открытия ленты Мёбиуса.

Когда я выбрала тему своей работы, то даже не подозревала, что подбирать и изучать материал будет так интересно. Мы живём и не задумываемся об окружающих нас предметах. А, оказывается, их можно рассматривать как топологические объекты и, по возможности, получать их друг из друга. Особенно мне понравилось проводить эксперименты над листом Мёбиуса, знакомясь при этом с его свойствами. Также интересно было узнать, что этот топологический объект нашёл применение в различных областях науки и техники.

Время не стоит на месте. Наука и техника движутся вперёд. Может быть, кто-то скоро откроет новые свойства листа Мёбиуса или новые топологические объекты, похожие на него. А может быть, для листа Мёбиуса найдётся новое применение в чём-то уже более грандиозном.

Список использованной литературы

1. В.А.Гусев «Внеклассная работа по математике в 6-8 классах»

2. С.П.Бобров «Архимедово лето», Москва: Детгиз, 1959 год

3. М.Гарднер «Математические чудеса и тайны», Москва: Наука, 1978 год

4. Н Ленгдон, Ч.Снейп «С математикой в путь», Москва: Педагогика, 1987 год

5. К.Е.Левитин «Геометрическая рапсодия», Москва: Знание, 1984 год

6. М.Гарднер «Математические досуги»

7. Б.А.Кардемский «Математическая смекалка»

8. А.А.Саркисян, Ю.М.Калягин «Познакомьтесь с топологией», Москва: Просвещение, 1976 год

9. Д.Я.Стрейк «Краткий очерк истории математики»

10. Ф.А.Брокгауз, И.А.Эфрон «Энциклопедический словарь», Санкт-Петербург: Типо-литография И.А.Эфрона, 1896 год

11. Н.Я.Виленкин и другие «За страницами учебника математики: Арифметика. Алгебра. Геометрия. Книга для учащихся 10-11 классов общеобразовательных учреждений», Москва: Просвещение: АО «Учебная литература», 1996 год

12. В.Г.Болтянский, В.А.Ефремович «Наглядная топология», Москва: Наука, 1985 год

13. Е.В.Коробенок, А.А.Столяр «Сколько сторон у поверхности? Беседы с учащимися 7-10 классов», Минск: Народная асвета, 1985 год

14. С.Барр «Россыпи головоломок», Москва: Мир, 1987 год

24