
Районная научно-практическая конференция
школьников «Первые шаги в науку»
Секция физико-математического цикла
Лист Мёбиуса и его свойства
Выполнил:
Камагурова Маргарита
Павловна
МКОУ Большеникольская СОШ Чулымского района, 9 класс
Научный руководитель:
Тараканова Лариса Альбертовна,
учитель математики высшей квалификационной категории
с. Большеникольское
Оглавление
| Введение | Стр. 3 |
| Глава I. Август Фердинанд Мёбиус. Историческая справка. | Стр. 4 |
| Глава II. Открытие листа Мёбиуса. | Стр. 5 |
| Глава III. Представление о листе Мёбиуса. | Стр. 5 |
| Глава IV. Свойства листа Мёбиуса. | Стр. 7 |
| Глава V. Применение ленты Мёбиуса. | Стр. 8 |
| Глава VI. Эксперименты с бумагой. | Стр. 10 |
| Выводы. Заключение. | Стр. 12 |
| Использованная литература. | Стр. 13 |
| Приложение 1. Гравюра с изображением муравья, ползающего по Ленте Мебиуса. | Стр. 14 |
| Приложение 2. Международный символ переработки, представляющий собой лист Мёбиуса. | Стр. 15 |
| Приложение 3. Фокусы с листом Мебиуса. | Стр. 16 |
Введение
В наше время актуально изучение различных свойств и нестандартных применений. Я рассмотрела применение листа Мебиуса в науке, технике и изучении свойств Вселенной. Уже сейчас лента Мебиуса находит различное применение в быту: абразивные ремни для заточки инструментов, красящие ремни для печатающих устройств, ременные передачи, магнитофонные ленты и т.д.
Кроме того, существует гипотеза, что наша Вселенная вполне вероятно замкнута в ту же самую ленту согласно теории относительности – чем больше масса, тем больше кривизна пространства. Более того, эта теория полностью согласуется с теорией относительности Эйнштейна и его предположением, что космический корабль, все время летящий прямо, может вернуться к месту старта, что подтверждает неограниченность и конечность Вселенной. Из этого можно сделать вывод о реальности теории зеркальных миров: ведь астронавты, совершившие путешествие по ленте Мебиуса и вернувшиеся в исходную точку, превратятся в зеркальных своих двойников.
Есть гипотеза, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса, и только поэтому генетический код так сложен для расшифровки и восприятия. Больше того, такая структура вполне логично объясняет причину наступления биологической смерти - спираль замыкается сама на себя и происходит самоуничтожение, или аннигиляция, как подтверждают физики. Они, кстати, утверждают также, что все оптические законы основаны на свойстве ленты Мебиуса, в частности, отражение в зеркале - это своеобразный перенос во времени, краткосрочный, длящийся сотые доли секунды, ведь мы видим перед собой зеркального своего двойника.
Исходя из вышесказанного, я ставлю перед собой следующие цели:
Показать, что лист Мебиуса – объект топологии.
Сформулировать свойства листа Мебиуса.
Рассмотреть применение листа Мебиуса на практике.
Глава I. Август Фердинанд Мёбиус.
Историческая справка
| 17 ноября 1790 года в Германии родился мальчик Август Фердинанд Мёбиус – здоровый и крепкий малыш. Как и все дети, он сначала научился ползать, потом ходить, позже говорить. Все шло и развивалось своим чередом. Школа, университет. Мальчику повезло: астрономию ему преподавал сам Гаусс, математику – Пфафф. Как-то незаметно для окружающих в 26 лет он стал профессором, руководителем астрономической лаборатории в Лейпцигском университете. Научные статьи, лекции, работа. Все как у обычного профессора университета. |
А вгуст Фердинанд Мёбиус вгуст Фердинанд Мёбиус (17.11.1790-26.9.1868), немецкий геометр и астроном, профессор Лейпцигского университета |
Рассеянного доброго чудака студенты боготворили. Он любил ошарашивать их неожиданными задачками и назначал лекции, к примеру, на два часа ночи, чтобы показать ночное небо во всей его красе.
С 1816 г. начал вести самостоятельные астрономические наблюдения в Плейсенбургской обсерватории, в 1818г. стал ее директором, позже - профессором Лейпцигского университета.
Известны труды по проективной геометрии. В частности, впервые ввел систему координат и аналитические методы исследования, установил существование односторонних поверхностей (листов Мёбиуса), многогранников, для которых неприменим «закон ребер» и которые не имеют объема. Мёбиус - один из основоположников теории геометрических преобразований, а также топологии, теории векторов и многомерной геометрии. Получил важные результаты в теории чисел (функция Мёбиуса).
Глава II. Открытие листа Мёбиуса
На улице шел дождь. Была выкурена трубка, выпита чашка любимого кофе с молоком. Вид из окна навевал тоску. В кресле сидел мужчина. Мысли были разные, но как-то ничего особенного не приходило на ум. Только в воздухе витало ощущение, что именно этот день принесет славу и увековечит имя Августа Фердинанда Мебиуса.
На пороге комнаты появилась любимая жена. Правда, она была не в хорошем расположении духа. Правильнее сказать, она была разгневана, что для мирного дома Мебиусов было почти так же невероятно, как три раза в год увидеть парад планет, и категорически требовала немедленно уволить служанку, которая настолько бездарна, что даже не способна правильно сшить ленту.
| 
| Хмуро разглядывая злосчастную ленту, профессор воскликнул: “Ай да, Марта! Девочка не так уж глупа. Ведь это же односторонняя кольцевая поверхность. У ленточки нет изнанки!” Эта история произошла в 1858 году. Открытая поверхность получила математическое обоснование и имя в честь описавшего ее математика и астронома. |
Лента вдохновила на подвиги не одного добряка-профессора. Взял ее на вооружение и цех парижских портных. Отныне в качестве экзамена для новичка, претендовавшего на зачисление в цех, было пришивание к подолу юбки тесьмы в форме ленты Мебиуса. Оценили по достоинству невольное изобретение Марты и учителя. Неугомонным нерадивым ученикам предлагалось покрасить стороны ленты Мебиуса в разные цвета. Пыхтя от усердия, школяры проводили за этим занятием немало времени.
Глава III. Представление о листе Мёбиуса
Лента Мебиуса положила начало новой науке – топологии. Слово это придумал Иоганн Бенедикт Листинг, профессор Геттингенского университета, который почти в тоже время, что и его лейпцигский коллега, предложил в качестве первого примера односторонней поверхности уже знакомую нам, единожды перекрученную, ленту. Наука эта молодая и потому озорная. Иначе не скажешь о тех правилах игры, которые в ней приняты. Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать – делать с ней всё что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло, все её свойства остались неизменными. Для него не имеют никакого значения ни расстояния, ни углы, ни площади. А что же его интересует? Самые общие свойства фигур, которые не меняются ни при каких преобразованиях, если только не случается катастрофы – “взрыва” фигуры. Поэтому иногда топологию называют “геометрией непрерывности”. Она известна и под именем “резиновая геометрия”, потому что топологу ничего не стоит поместить все свои фигуры на поверхность детского надувного шарика и без конца менять его форму, следя лишь за тем, чтобы шарик не лопнул. А то, что при этом прямые линии, например, стороны треугольника, превратятся в кривые, для тополога глубоко безразлично.
Лист Мёбиуса иногда называют прародителем символа бесконечности  , так как, находясь на поверхности ленты Мёбиуса, можно было бы идти по ней вечно. Это не соответствует действительности, так как символ
, так как, находясь на поверхности ленты Мёбиуса, можно было бы идти по ней вечно. Это не соответствует действительности, так как символ  использовался для обозначения бесконечности в течение двух столетий до открытия ленты Мёбиуса.
использовался для обозначения бесконечности в течение двух столетий до открытия ленты Мёбиуса.
Лента Мёбиуса - бумажная лента, повернутая одним концом на полоборота (то есть на 180 градусов), и склеенная с его другим концом.

Поверхность ленты Мёбиуса имеет только одну сторону. Это легко проверить. Возьмите карандаш, и начните закрашивать ленту в каком-нибудь направлении. Вскоре вы вернетесь в то место, откуда начали. А теперь поглядите внимательно: закрашенной оказалась вся лента целиком! А ведь вы ее не переворачивали, чтобы закрасить с другой стороны. Да и не смогли бы перевернуть, даже если бы очень захотели, потому как поверхность ленты Мёбиуса - односторонняя. Такое вот у нее любопытное свойство наблюдается.
Что же из этого свойства следует? А следует удивительное превращение ленты.
Е сли разрезать ее вдоль, точно посередине - получится не две, а одна лента. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получится два кольца - но!- одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма «затейливое» переплетение двух колец – одинаковых по размеру, но разных по ширине.
сли разрезать ее вдоль, точно посередине - получится не две, а одна лента. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получится два кольца - но!- одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма «затейливое» переплетение двух колец – одинаковых по размеру, но разных по ширине.
Н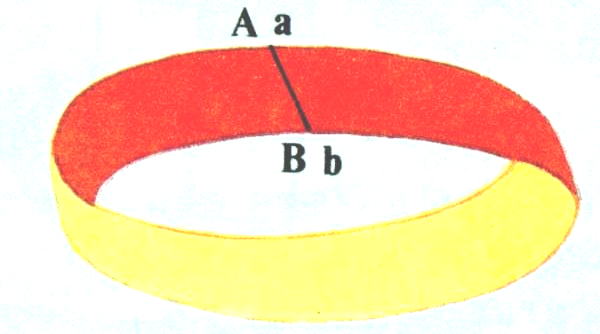 у а что, интересно, получится, если перед склеиванием ленты перекрутить ее два раза (то есть на 360 градусов)? Такая поверхность будет уже двусторонней. И чтобы закрасить все кольцо целиком, вам придется непременно перевернуть ленту на другую сторону.
у а что, интересно, получится, если перед склеиванием ленты перекрутить ее два раза (то есть на 360 градусов)? Такая поверхность будет уже двусторонней. И чтобы закрасить все кольцо целиком, вам придется непременно перевернуть ленту на другую сторону.
Если разрезать ее вдоль посередине, то вы получите два одинаковых кольца, но опять же сцепленных между собой. А, разрезав каждое из них еще раз вдоль посередине, вы обнаружите уже четыре кольца, соединенных друг с другом. Можно теперь рвать эти кольца по очереди, и всякий раз оставшиеся будут по - прежнему сцеплены вместе.
И действительно: простая полоска бумаги, но перекрученная всего лишь раз и склеенная затем в кольцо, сразу же превращается в загадочную ленту Мёбиуса и приобретает удивительные свойства.
Опыт № 1. Начала красить лист Мёбиуса, не переворачивая его.
Результат. Лист Мёбиуса закрасился полностью.
«Если кто-нибудь вздумает раскрасить только одну сторону поверхности мёбиусовой ленты, пусть сразу погрузит её всю в ведро с краской», - пишет Рихард Курант и Герберт Робинс в превосходной книге «Что такое математика?»
Опыт№ 2. На внутреннюю сторону обычного кольца посадила бумажного Паука, а на наружную - бумажную муху, разрешила ползать как угодно, запретив перелазить через края кольца.
Результат. Паук не сможет добраться до мухи.
Опыт № З. Посадила муху и паука на лист Мебиуса, разрешила ползать как угодно, не перелазив через края.
Результат. Паук догнал и съел муху.
| Опыт №4. Вырезала из бумаги солдатика и отправил его вдоль пунктира, идущего по середине листа Мебиуса с поднятым вверх флажком. Результат. Солдатик вернулся в то же место, откуда начал движение, но в перевернутом виде, флажок опущен вниз. | 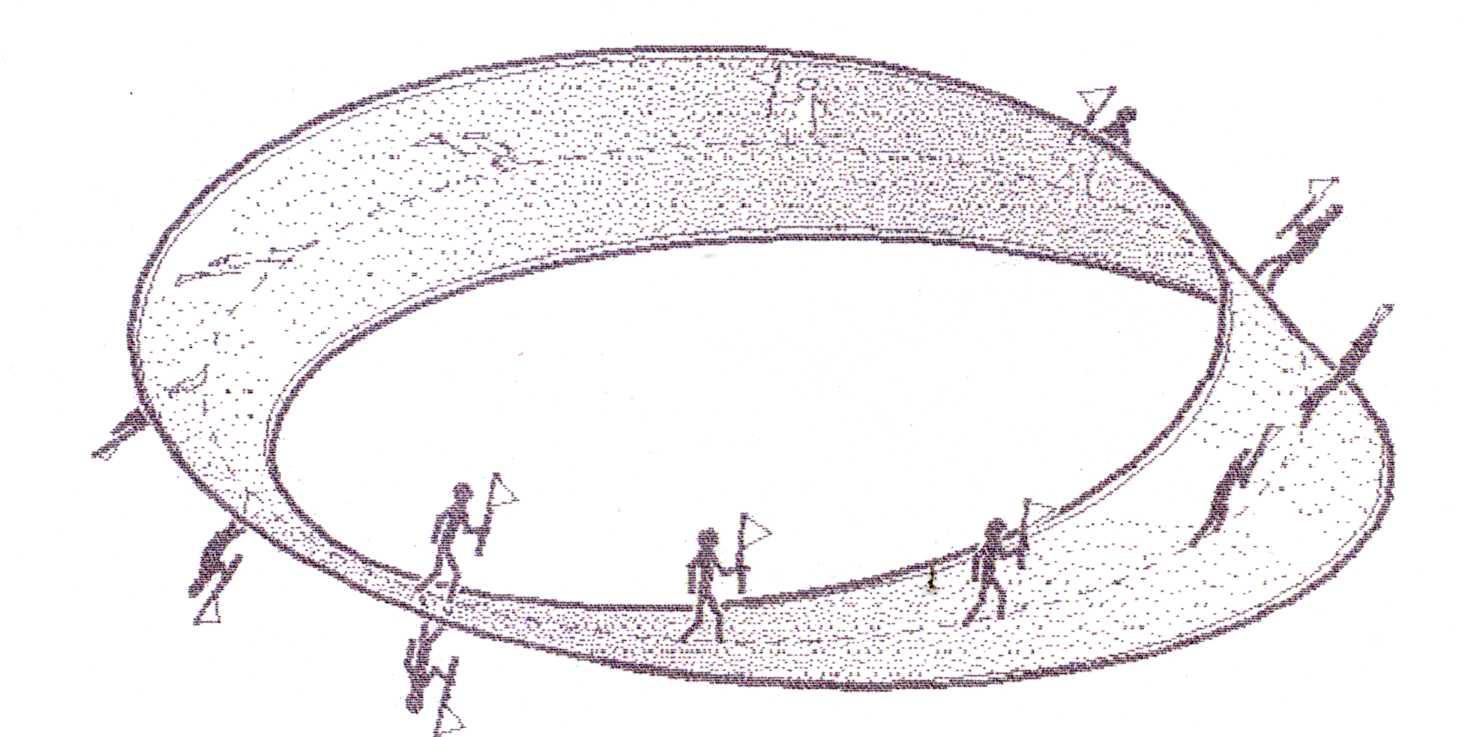 |
Глава IV. Свойства листа Мёбиуса
Лист Мёбиуса – топологическая фигура, имеет один край и одну сторону, не меняет своих свойств, пока его не разрежут или не склеят.
Односторонность – топологическое свойство листа Мёбиуса, характерное только для него. Если двигаться по поверхности Ленты Мебиуса в одном направлении, не пересекая ее границ, то, в отличие от двусторонних поверхностей (например, сферы и цилиндры), попадаешь в место, перевернутое по отношению к исходному. Если двигать по этой ленте окружность, одновременно обходя ее по часовой стрелке, то в начальном положении направление обхода станет против часовой стрелки.
Непрерывность – это ещё одно топологическое свойство. С топологической точки зрения круг неотличим от квадрата или треугольника, потому что их легко преобразовать один в другой, не нарушая непрерывности. На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом муравью на гравюре Эшера (Приложение 1) ни разу не придётся переползать через край “ленты”. Разрывов нет – непрерывность полная.
Связность. Если квадрат полоснуть бритвой от стороны к стороне, то он, естественно, распадётся на два отдельных куска. Точно также любой удар ножом разделит яблоко на две части. Но вот чтобы разделить кольцо на две части, нужно уже два разреза. И два раза придётся резать бублик, если вы хотите угостить им двух друзей. Телефонный диск можно десять раз рассечь ножом от одной замкнутой кривой до другой, а он останется единым целым. Поэтому любой тополог скажет вам, что квадрат и ромашка – односвязны, кольцо и оправа от очков – двусвязны, а всяческие решётки, диски с отверстиями и подобные сложные фигуры – многосвязны. Ну, а наш лист Мёбиуса? Конечно двусвязен, т.к. если разрезать его вдоль, он превратится не в два отдельных кольца, а в одну целую ленту. Если перекрутить ленту на два оборота, то лист становится односвязным. Три оборота – связность снова равна двум и т.д.
Ориентированность- свойство, отсутствующее у листа Мёбиуса. Так, если бы человек смог пропутешествовать по всем изгибам листа Мёбиуса, то когда он вернулся бы в исходную точку, он превратился в своё зеркальное отражение.
«Хроматический номер». Он равен максимальному числу областей, которые можно нарисовать на поверхности так, чтобы каждая из них имела общую границу со всеми другими. Если каждую такую область выкрасить по-разному, то любой цвет должен соседствовать с любым другим. Так вот, на листе бумаги, даже если его склеить в кольцо, ещё никому не удалось расположить пять цветных пятен любой формы, которые имели бы всеобщую границу. И на сфере, и на цилиндре их может быть не более четырёх. Это и значит что хроматический номер этих поверхностей – четыре. А на бублике число соответствующих цветов равняется семи. Каков же хроматический номер листа Мёбиуса? Он, как ни поразительно, равен шести.
Глава V. Применение ленты Мёбиуса
Чудесные ее свойства тут же породили множество научных трудов, изобретений (весьма полезных и совершенно нереальных), а также многочисленных фантастических рассказов. В рассказе А.Дейча “Лента Мебиуса” описывался случай в Нью-йоркском метро. Однажды случилось так, что пути метрополитена пересеклись, и весь он стал напоминать огромную ленту Мебиуса. Поезда один за другим стали исчезать, появляясь снова только через несколько месяцев. А Козьма Прутков подарил читателям афоризм: "Где начало того конца, которым оканчивается начало?"
Целую серию скульптур в виде листа Мебиуса создал скульптор Макс Билл. Довольно много разнообразных рисунков оставил Мауриц Эшер. Особенно интересна гравюра с изображением муравья, ползающего по Ленте Мебиуса (Приложение 1). Международный символ переработки представляет собой Лист Мёбиуса (Приложение 2).
Существовали технические применения ленты Мёбиуса. Полоса ленточного конвейера выполнялась в виде ленты Мёбиуса, что позволяло ему работать дольше, потому что вся поверхность ленты равномерно изнашивалась. Также в системах записи на непрерывную плёнку применялись ленты Мёбиуса (чтобы удвоить время записи). В матричных принтерах красящая лента также имела вид лист Мёбиуса для увеличения срока годности.
Устройство под названием резистор Мёбиуса — это недавно изобретённый электронный элемент, который не имеет собственной индуктивности. Никола Тесла запатентовал подобное устройство в начале 1900-х. Катушка для Электромагнитов предназначалась для использования в его системе глобальной передачи электричества без проводов.
У входа в музей истории и техники в Вашингтоне медленно вращается на пьедестале стальная лента, закрученная в полвитка. И это не случайно. Патентная служба зарегистрировала немало изобретений, в основе, которых лежит всё та же односторонняя поверхность.
В 1923 году выдан патент изобретателю Ли де Форесу, который предложил записывать звук на киноленте без смены катушек, сразу с двух сторон. Придуманы кассеты для магнитофона, где лента перекручивается и склеивается в кольцо, при этом появляется возможность записывать или считывать информацию сразу с двух сторон, что увеличивает ёмкость кассеты и соответственно время звучания.
В 1969 году советский изобретатель Губайдуллин предложил бесконечную шлифовальную ленту в виде листа Мёбиуса. В 1971 году изобретатель с Урала Чесноков П.Н. применил фильтр в виде листа Мёбиуса.
Мёбиусовая лента понравилась не только математикам, но и фокусникам. Более 100 лет лист Мёбиуса используется для показа различных фокусов и развлечений. Удивительные свойства листа демонстрировались даже в цирке, где подвешивались яркие ленты, склеенные в виде листов Мёбиуса. Фокусник закуривал сигарету и горящим концом дотрагивался до средней линии каждой ленты, которая была выполнена из калийной селитры. Огненная дорожка превращала первую ленту в более длинную, а вторую - в две ленты, продетая одна в другую. (В этом случае фокусник разрезал лист Мёбиуса не посередине, а на расстоянии в одну треть его ширины). Мною был изучено проведение фокуса с использованием ленты Мёбиуса (Приложение 3).
Скольких людей приводили в восторг аттракционы “Американские горки”…
И это только ничтожная часть примеров использования этой удивительной поверхности.
Глава VI. Эксперименты с бумагой
Эксперимент 1.Перед склеиванием концов бумажной полосы прорежем щель в полосе, проденем сквозь нее один из ее концов, а затем продолжим разрез вдоль всей ленты.

Результат: два листа Мебиуса.
Эксперимент 2. Приготовим два кольца: одно обычное и одно Мебиусово. Склеим их под прямым углом, а затем оба разрежем вдоль.

Результат: прямоугольная плоская рамка.
Эксперимент 3. Возьмем бумажную полоску. Ее концы перед склеиванием разрежем и перекрутим так, как это показано на рисунке.
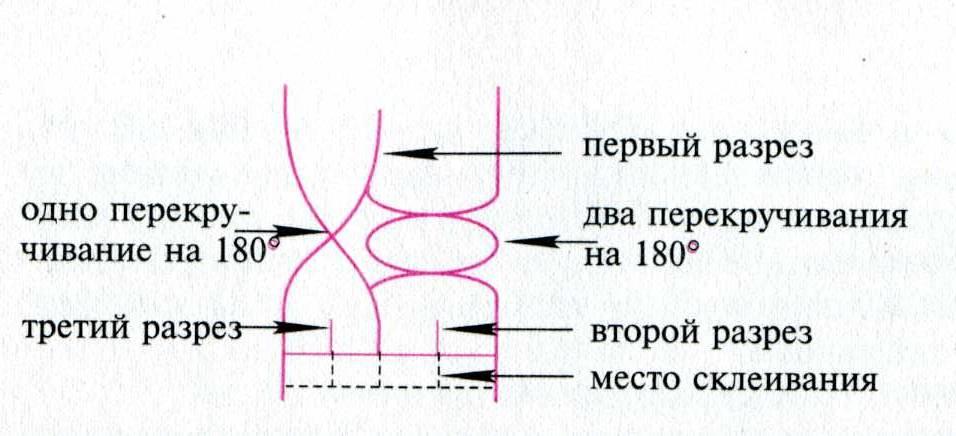
Каждая половинка концов перекручивается по-разному, и после склеивания концов выполняются два разреза по средней линии каждой половины бумажной полосы.
Результат: бумажное кольцо распадется на два отдельных кольца, одно из которых при разрезании посредине превращается в два отдельных кольца, а другое — в одно большое.
Эксперимент 4. Трижды перекрученную бумажную ленту проденем сквозь перстень, склеим концы, а затем разрежем по средней линии.
Результат: одно большое бумажное кольцо с узлом, завязанным вокруг перстня.
Выводы:
Лист Мебиуса имеет один край.
Лист Мебиуса имеет одну сторону.
Лист Мёбиуса - топологический объект. Как и любая топологическая фигура лента Мёбиуса не меняет своих свойств, пока ее не разрывают или не склеивают его отдельные куски.
Один край и одна сторона листа Мебиуса не связаны с его положением в пространстве, не связаны с понятиями расстояния
Заключение.
Лист Мёбиуса - первая односторонняя поверхность, которую открыл учёный Август Фердинанд Мёбиус. Позже математики открыли ещё целый ряд односторонних поверхностей. Но эта - самая первая, положившая начало целому направлению в геометрии, по - прежнему привлекает к себе внимание учёных, изобретателей, художников.
В этой работе я пыталась описать свойства этой прекрасной поверхности – листа Мебиуса, показать его значимость на практике, доказать, что лист Мёбиуса - топологическая фигура.
Конечно же, главная ценность листа Мёбиуса состоит в том, что он дал толчок новым обширным математическим исследованиям. Именно поэтому его часто считают символом современной математики.
Использованная литература.
Гарднер М. Математические чудеса и тайны. – М.:Наука,1978.
Смирнова Е.С. Курс наглядной геометрии: Методическая разработка для 6 кл.: Кн.для учителя. – М.:Просвещение, 2002
Шарыгин И.Ф., Еранжиева Л.Н. Наглядная геометрия: 5-6 кл. – М.: Дрофа, 2000.
Нагибин Ф.Ф., Канин Е.С.. Математическая шкатулка. – М.: Просвещение, 1988.
Энциклопедия для детей. Математика. – М.: Аванта+, 2001.
Лэнгдон Н., Снейт Ч. С математикой в путь. – М.: Педагогика, 1987.
Стюарт Я. Топология// Квант. – 1992. - №7.
Приложение 1.

Мауриц Эшер.
Гравюра с изображением муравья, ползающего по Ленте Мебиуса.
Приложение 2.

Международный символ переработки представляет собой Лист Мёбиуса.
Приложение 3.
Фокусы с листом Мебиуса
Бумажные кольца
Хорошо всем известный «лист Мёбиуса» используется на протяжении последних 75 лет для многих фокусов. В одном из них показывающий вручает зрителю три больших бумажных кольца, каждое из которых получилось путем склеивания концов длинной бумажной ленты. Зритель разрезает ножницами первое кольцо вдоль ленты посередине, пока не вернется в исходную точку. В результате получаются два отдельных кольца. Разрезая таким же образом второе кольцо, он получает, к своему удивлению, не два кольца, а одно, которое вдвое длиннее исходного. Наконец, разрезая третье, он снова получает поразительный результат: два кольца, сцепленных друг с другом. Результат этого фокуса зависит от того, как были сомкнуты концы ленты перед склейкой. Первое наше кольцо получилось путем простого соединения концов ленты без перекручивания. Второе кольцо (его называют листом Мёбиуса) получается при соединении концов ленты, перекрученной один раз на 1800. Одним из наиболее любопытных свойств этой поверхности, имеющей только одну сторону и один край, является то, что, разрезая ее вдоль посередине, мы получаем одно большое кольцо, если же разрезать его не посередине, а на расстоянии в одну треть ширины от края, то получается два кольца: одно большое и сцепленное с ним маленькое. Третье кольцо получилось при разрезании ленты, концы которой перекручивались перед склейкой дважды, т. е. на 360°.
В другом варианте фокуса кольцо разрезается на два отдельных кольца, одно из которых при разрезании посередине превращается тоже в два отдельных кольца, а другой — в одно большое. Оригинальный метод приготовления кольца для такого фокуса показан на рис. 4, а его улучшение — на рис. 5. Для склеивания концов употребляется какой-нибудь быстросохнущий клей.
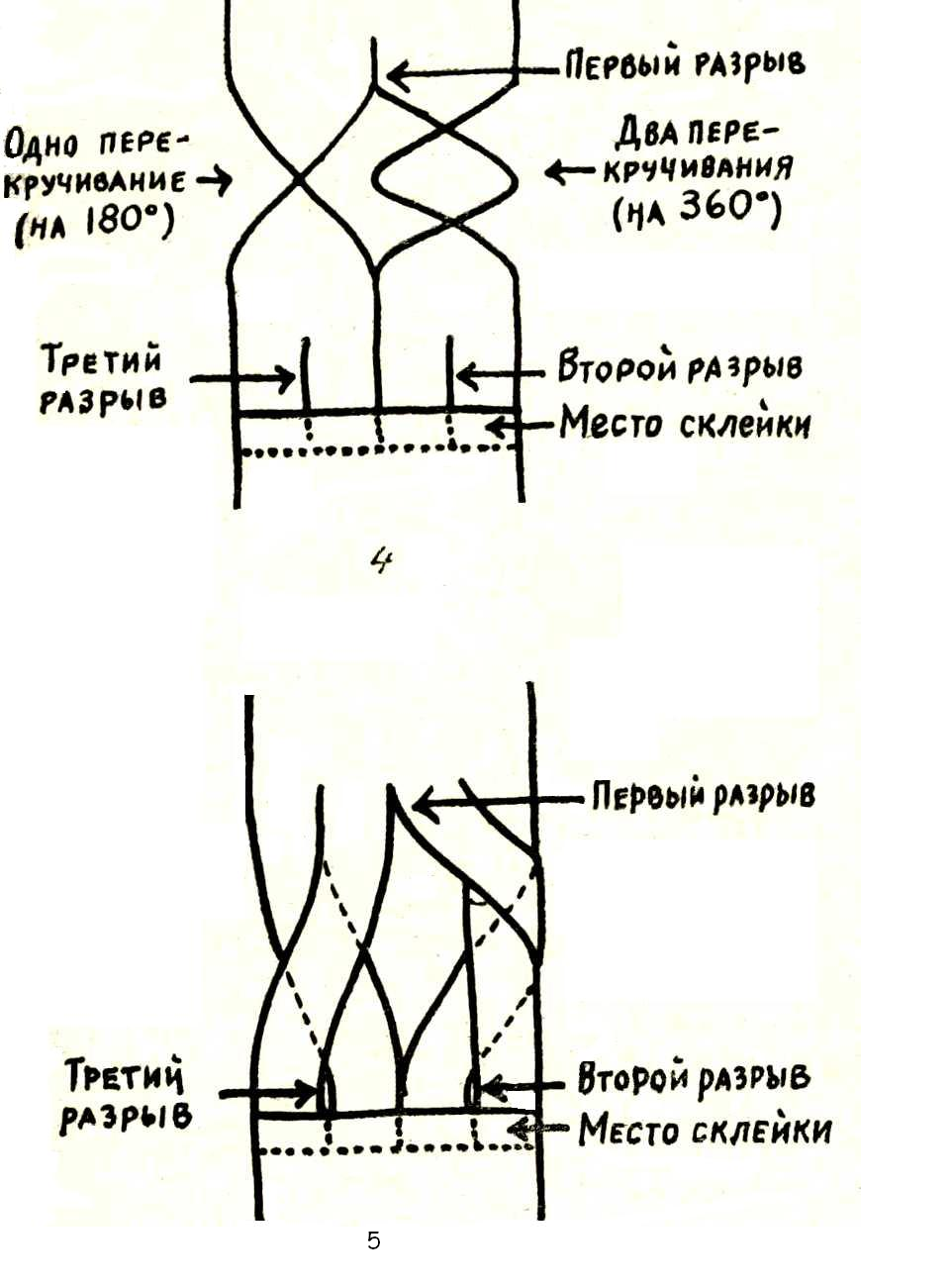
С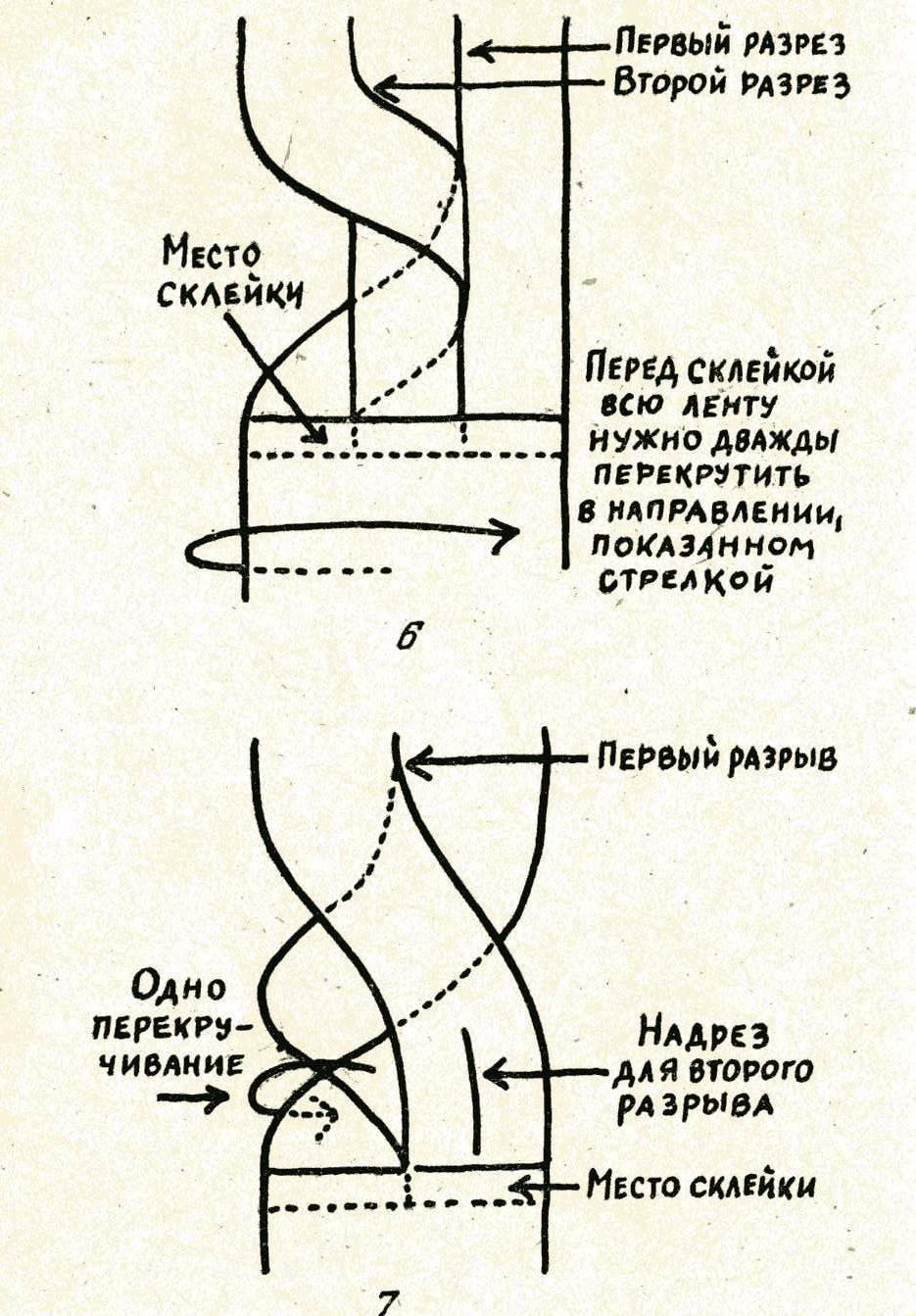 пособ приготовления бумажной ленты, при котором после двух разрезов получается цепочка из трех сцепленных колец, изображен на рис. 6.
пособ приготовления бумажной ленты, при котором после двух разрезов получается цепочка из трех сцепленных колец, изображен на рис. 6.
Если изготовить кольцо так, как показано на рис. 7, то после первого разрывания (разрезания) получится большое кольцо, размер которого вдвое больше первоначального, а второе разрывание даст кольцо вчетверо длиннее исходного. Другой вариант изображен на рис. 8, первое разрывание дает одно большое кольцо, а второе — два сцепленных.
| 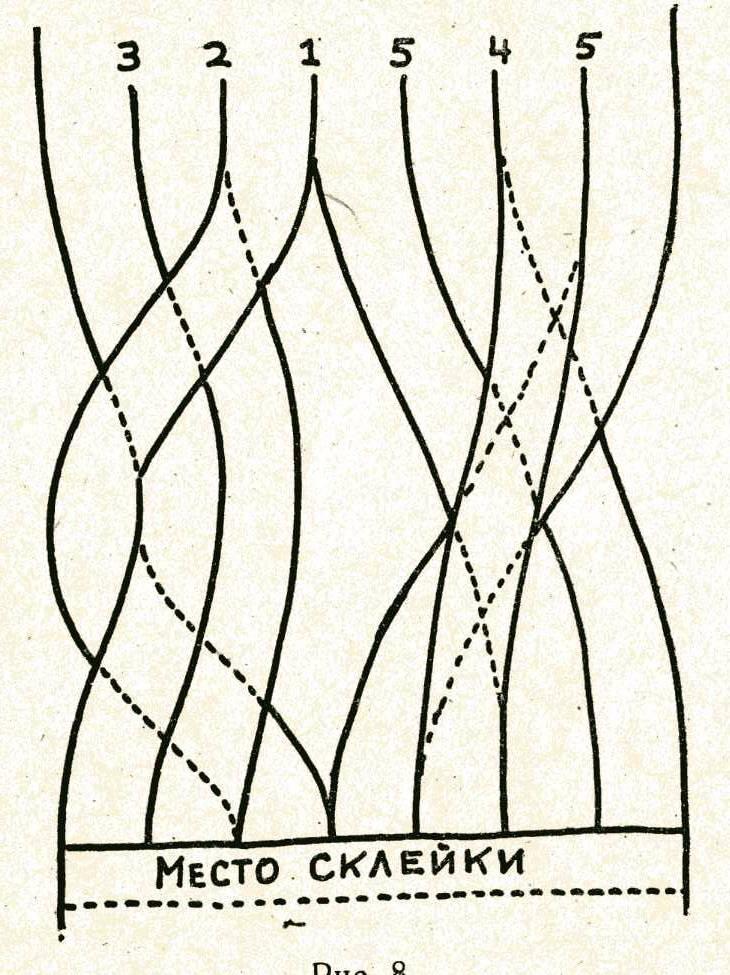
Рис.8 | 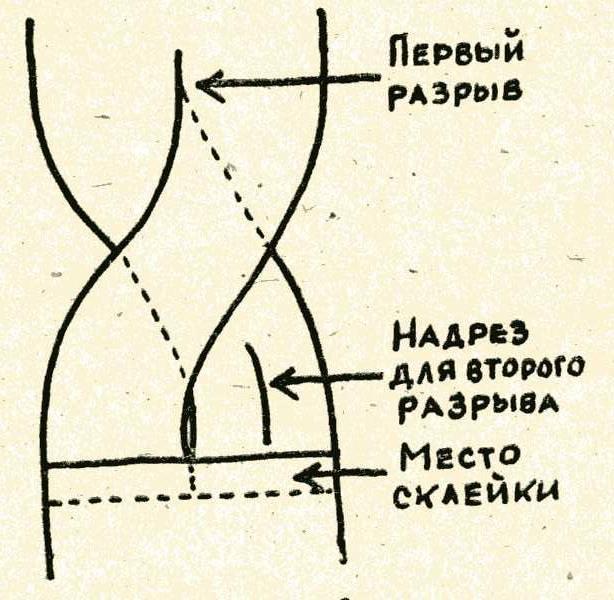
Рис.9 |
Можно придумать и другие комбинации. Например, после разрывания кольца, изображенного на рис. 9, получаются два отдельных кольца. Разрывание одною из них дает цепочку из трех колец, разрывание другого — одно большое кольцо. Это последнее кольцо можно разрывать еще раз, причем получится еще большее кольцо.
Если трижды перекрученную ленту продеть сквозь перстень, склеить концы, а затем разрезать или разорвать вдоль посередине, то получится одно большое кольцо с узлом, завязанным вокруг перстня.
Странные кольца
Отрежьте от газеты во всю ширину обеих ее страниц три полоски шириною по 3—4 см; поставьте на их концах цифры, как это показано на рисунке.
Смазав концы одной полоски клеем, сделайте такое кольцо, как на рисунке А Цифру 3 надо при этом наложить на цифру 1, а 2 — на 4. Возьмите другую полоску и, повернув один ее конец на полоборота, склейте второе кольцо; вам станет ясно, как теперь надо соединить края полоски, если вы посмотрите на рисунок Б.
Для последнего кольца нужно третью полоску перекрутить на полный оборот, благодаря чему при склеивании концы ее будут сходиться в том же положении, как в первом кольце (рис. В).
Сделав кольца, окрасьте их чернилами с обеих сторон. Темный цвет не даст зрителям возможности разглядеть, что два кольца склеены из перекрученных полосок.
Держа кольца в руке, вы показываете их зрителям. Потом берете ножницы и спрашиваете: «Что получится, если разрезать кольцо вдоль по средней линии?» (линия разреза обозначена на рис. Г пунктиром). При этом вы оставляете в руке только второе кольцо, а два других кладете на стол. На ваш вопрос зрители, безусловно, ответят, что получатся два отдельных кольца, и будут удивлены, увидев после разрезания одно, но двое большего размера, чем то кольцо, которое вы держали в руке (рис Д).
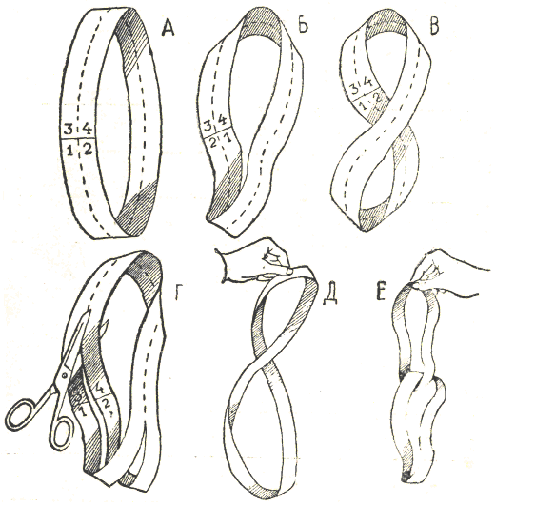
Дайте любому из зрителей ножницы и первое кольцо и предложите его разрезать так же, как это» - сделали - вы. На этот раз ничего необычайного не произойдет. Зрители увидят два отдельных кольца.
Отослав своего незадачливого соперника на место, вы говорите: «Я сейчас применю новый способ и разрежу третье кольцо гак» что из одного получатся два». Зрители наверняка заявят, что они это видели только сейчас, что это неинтересно Вы разрезаете кольцо и показываете два... соединенных между собою, как звенья цепи (рис. Е).
19






 вгуст Фердинанд Мёбиус
вгуст Фердинанд Мёбиус

 сли разрезать ее вдоль, точно посередине - получится не две, а одна лента. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получится два кольца - но!- одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма «затейливое» переплетение двух колец – одинаковых по размеру, но разных по ширине.
сли разрезать ее вдоль, точно посередине - получится не две, а одна лента. А вот если разрезать ленту на расстоянии 1/3 ее ширины от края, то получится два кольца - но!- одно большое и сцепленное с ним маленькое. Если же разрезать еще и маленькое кольцо вдоль посередине, то у вас окажется весьма «затейливое» переплетение двух колец – одинаковых по размеру, но разных по ширине.  у а что, интересно, получится, если перед склеиванием ленты перекрутить ее два раза (то есть на 360 градусов)? Такая поверхность будет уже двусторонней. И чтобы закрасить все кольцо целиком, вам придется непременно перевернуть ленту на другую сторону.
у а что, интересно, получится, если перед склеиванием ленты перекрутить ее два раза (то есть на 360 градусов)? Такая поверхность будет уже двусторонней. И чтобы закрасить все кольцо целиком, вам придется непременно перевернуть ленту на другую сторону. 






 пособ приготовления бумажной ленты, при котором после двух разрезов получается цепочка из трех сцепленных колец, изображен на рис. 6.
пособ приготовления бумажной ленты, при котором после двух разрезов получается цепочка из трех сцепленных колец, изображен на рис. 6.





























