Исследовательская работа «Извлекать корни квадратные – дело очень занятное»

Муниципальное общеобразовательное учреждение

«Займищенская средняя общеобразовательная школа имени Ф. Г. Светика»

243111, Брянская область, г. Клинцы, ул. Клинцовская, д.102 а,

Конкурс

Учебно - исследовательских и проектных работ обучающихся

Направление
«Точные науки»

Исследовательская работа

«Извлекать корни квадратные – дело очень занятное»

Автор:  Зябкина Анастасия Павловна
Ученица 7а класса

МБОУ-Займищенской СОШ
Руководитель: Рябых Надежда Владимировна

учитель математики МБОУ-Займищенской СОШ

Адрес места работы: 243111 с. Займище,

ул. Клинцовская, д.102а
Телефон: 8 9529624608

г. Клинцы  2020

Содержание

Введение........................................................................... 3

Основная часть

Глава 1. Что нужно знать, чтобы корни извлекать

1.1 Вместо предисловия

1.2 .Мгновенное возведение в квадрат...................................4….
1.3. 6 волшебных цифр .................................................. 5
Глава 2. Готовимся к ЕГЭ

1.1. Способ разложения на простые множители .................. .6

1.2 Извлечение квадратного корня уголком ………………6

1.3 …и ещё один способ………………………………………7
Заключение...........................................................................8

Список источников..........................9

Приложения ........................................................................10-11

Введение:
Почему я выбрала эту тему  для своего исследования?
Так уж получилось, что когда мы с мамой смотрели по телевизору программу «Лучше всех!» (это моя любимая передача), я увидела маленьких ребят, которые могли устно посчитать трудные примеры. Нас всех это удивило. И я подумала, почему я так не смогу!
А когда мой учитель математики проверял самостоятельную работу у старшеклассников, то я услышала выражение «Извлечь корень». Мне стало интересно вдвойне, и я решила всё подробно узнать у учителя. Надежда Владимировна меня поддержала. И я готова была окунуться с головой в эту, пока ещё непонятную для меня область математики.

Основная цель работы: исследовать способы вычисления арифметических корней и найти самый рациональный для практического применения.
Задачи:
- ознакомиться с необходимой теорией
- провести опрос , одноклассников, учащихся школы, учителей; родственников
- сравнить  и проанализировать собранный материал.

Методы исследования:

- беседа с учителями математики, учащимися школы; родителями
- обсуждение, уточнение  и корректировка  полученной информации.
Новизна проекта.
Очень хочется удивлять и  самой удовольствие получать!

Основная часть
Глава 1. Что нужно знать, чтобы корни извлекать

1. Вместо предисловия

Выбрав очень интересную для меня тему для исследования, я снова обратилась к изданию «В царстве смекалки» В предисловии к своему первому изданию «В царстве смекалки» Емельян Игнатьевич Игнатьев пишет: «Сообразительность, смекалку» нельзя ни «вдолбить» , ни «вложить» ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме.

Во время работы над исследованием я обнаружила интересную информацию. Оказывается, существует неофициальный праздник, посвящённый квадратному корню. Он отмечается 9 раз в столетие, когда и число, и порядковый номер месяца являются квадратным корнем из двух последних цифр года. Например: 02.02.04. Впервые праздник отмечался 9 сентября 1981 года. Ближайший праздник - 05.05.2025.
Далее я провела анкетирование  с ребятами школы. Результаты анкетирования учащихся подтвердили мою догадку о том, что большинство ребят не умеют извлекать квадратных корней без таблицы квадратов. (Приложение 1)
Вывод:  кропотливая  работа по исследованию истории  этого вопроса  - это только начало. Впереди меня ожидали более серьёзные исследования.

1. Мгновенное возведение в квадрат

Научиться быстро извлекать корни квадратные без калькулятора - дело не простое. Поэтому мне пришлось обратиться сначала к интернет-ресурсам. Занятие это оказалось очень не простым для всей нашей семьи, так как в этом деле мне помогали и мама, и папа. Я узнала, что существуют различные способы извлечения квадратных корней. Но оказалось, что без учителя математики разобраться в этом было не так –то просто. И я обратилась за помощью к моему учителю, Рябых Надежде Владимировне. Она напомнила мне некоторые приёмы быстрого счёта, необходимые при решении этого вопроса.

Чтобы возвести двухзначное или трехзначное число, заканчивающееся на 5 во вторую степень, необходимо первое число умножить на это же число, к которому прибавлена единица, и в конце записи поставить 25.

Например:

1) 65² = 6 * (6 + 1) 25 = 4225

2) 35² = 3 * (3 + 1) 25 = 1225

3) 125² = 12 * (12 + 1) 25 = 15625

А также порекомендовала выучить таблицу квадратов чисел от 11 до 31. Что я и сделала. …И запомнить 6 волшебных цифр.

1.2. 6 волшебных цифр

• Последняя цифра квадрата в десятичной записи может быть равной 0, 1, 4, 5, 6,9

• 1 получится, если возвести в квадрат число, оканчивающееся 1 или 9, 4 – 2 или 8, 5 – только5, 6 _ 4 или 6, 9 – 3 или7.

Глава 2. Готовимся к ЕГЭ

1.1Метод разложения на простые множители

Этот метод мы изучали в 6 классе. Я обратилась к учебнику математики и в памяти всё всплыло.

1936 │2 1521│3

968│2 507│3

484│2 169│13

242│2 13│13

121│11 1│1

11│11

1│1

√1936 = √2⁴∙11² = 2∙2∙11 = 44 √1521 = √13² ∙ 3²= 13∙3 = 39

Но если взять большее число, пятизначное или шестизначное, то быстро разложить на простые множители не получится. Например, я очень долго возилась с числом 17 956, пока нашла подходящие простые числа.

А вот другим способом я легко извлекла из него корень.

Вывод: этот метод можно применять лишь в самых простых случаях. Могу сказать однозначно, что у меня он не вызвал большого интереса.

1.2 Извлечение квадратного корня уголком.
- Возьмём число 5 963 364. Разобьём его по 2 цифры справа налево; .
- Извлечём квадратный корень из 5, получаем 2 с недостатком. Цифра 2 –это первая цифра корня.
- Число 2 возведём в квадрат и вычитаем из 5, получаем 1 – первый остаток.
- К остатку 1 сносим цифры 9 и 6 второй группы 96, получаем число 196.

-Удваиваем первую цифру корня 2 и, записывая слева, получаем - 4

    - К числу 4 нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 196, либо меньше его. Это цифра 4 – вторая цифра корня.

 - Находим остаток 196 – 176= 20. Сносим снова 2 цифры 33, получаем 2033.

-Удваиваем 24, пишем слева и приписываем цифру и снова умножаем так, чтобы получить число равное или близкое к 2033. Это цифра 4. Получаем 1936. 4 - третья цифра корня.

-Вычитаем из 2033 1936, получаем 97. Сносим 64, получили 9764

-Удваиваем 244, пишем слева, приписываем 2 и умножаем на 2, получили 9764. Итак – 2 последняя цифра корня из 5963364.

Вывод: этот способ очень интересен для меня, и я попробую научиться извлекать корни таким образом.

-

1.3 …И ещё один способ

Здесь мы будем использовать последнюю цифру числа и умение возводить в квадрат число, оканчивающееся на «5». (Приложение)

Заключение

В наш век новых технологий и массовой компьютеризации умение осуществлять в уме сложные математические вычисления и операции является важным элементом для развития логического мышления.

При подготовке материалов к исследовательской работе, я получила знания, позволяющие развиваться в творческой и исследовательской деятельности. Продемонстрировала одноклассникам приемы быстрого счета, тем самым заинтересовала их в необходимости развития возможностей нашего мозга в тех сферах, которые раннее казалось были недоступны. Представленные мной методы устного извлечения квадратных корней помогают достаточно быстро без применения дополнительных, в том числе электронных средств вычисления, осуществлять расчет сложных задач, дают понимание (суть) математических процессов, тем самым приоткрывая завесу тайн Царицы наук математики.

В результате быстрый счет помогает не только проводить сложные математические операции и расчеты, необходимые для дальнейшей подготовки к ЕГЭ и дальнейшей профессиональной деятельности, но и развивает гибкость ума, приучая в разных ситуациях находить неординарные решения.

Список литературы:

1. Вроблевский. Как научиться легко и быстро считать. - М.-1932.-132с.

2. Просветов Г.И. «Быстрый счет: задачи и решения» - М., 2008.

3.Сорокин А. С. Техника счета. М., "Знание", 1976.

Интернет ресурсы:

1. http://4brain.ru/schitat-v-ume/

2. http://ru.wikipedia.org/wiki

Приложение 1

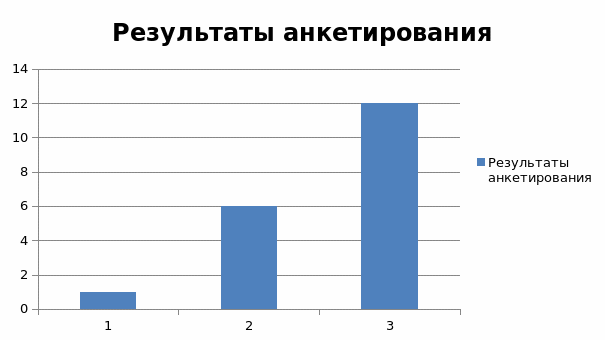
1)Кто из вас сможет извлечь корень квадратный из четырехзначных и пятизначных чисел без калькулятора?

2)Можете ли вы устно возводить во вторую степень двухзначные числа, оканчивающиеся на 5?

3)Кто хочет этому научиться?

Приложение2
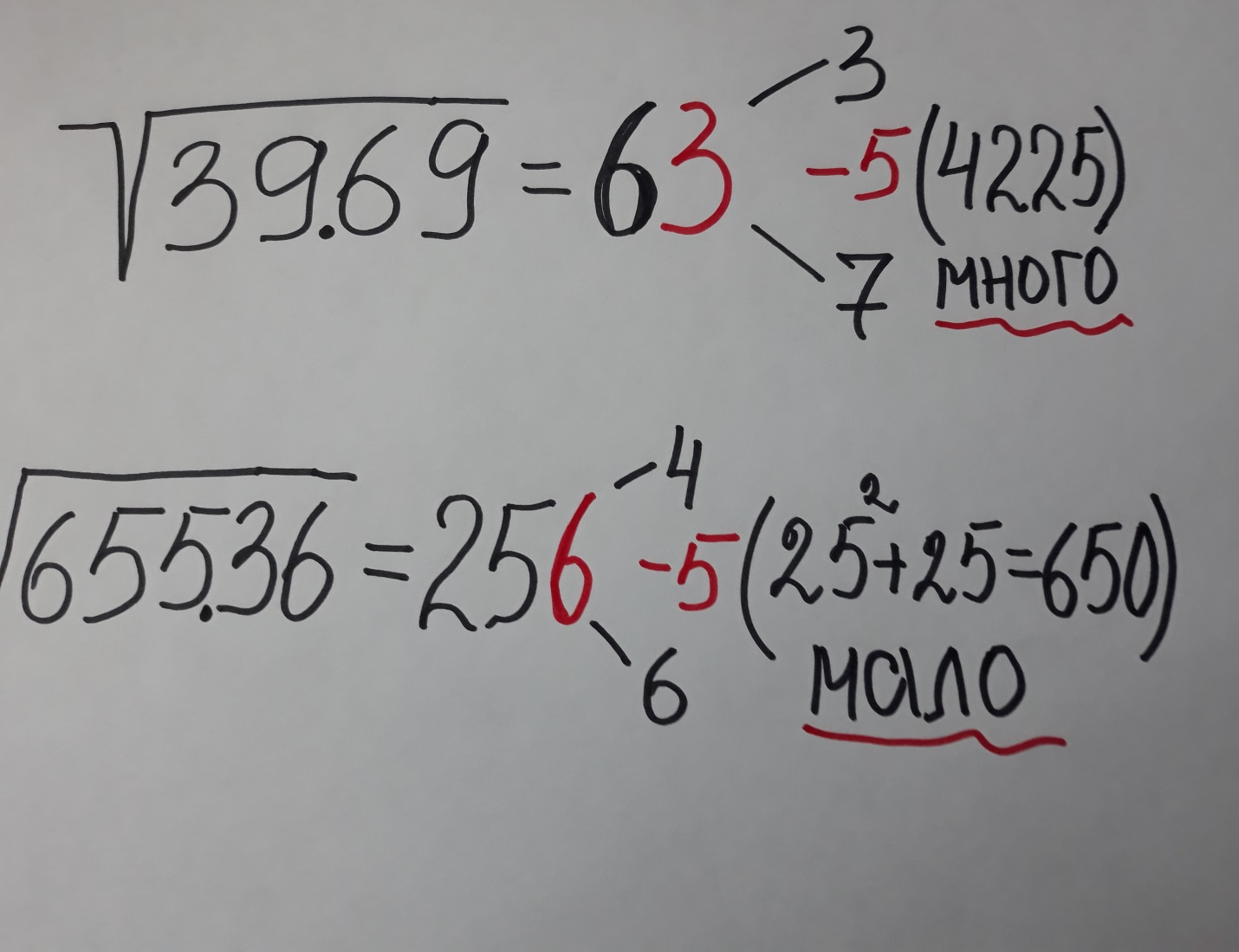