Исследовательская работа "Круги Эйлера" теория

Исследовательская работа

«Круги Эйлера»

Авторы: Горковенко Мария

Лущик Милана

ученицы 8 класса «Б»

МАОУ СОШ №4 г.Черняховска

Руководитель: Вязимова

Любовь Михайловна

учитель математики

г.Черняховск – 2019

Цель нашей исследовательской работы:

1) Выявление задач, которые можно решать с помощью кругов Эйлера.

2) Научиться решать задачи, используя круги Эйлера.

Задачи исследования:

1) Изучить теоретические сведения по теме "Круги Эйлера";

2) Посмотреть применение "кругов Эйлера" в реальной жизни.

Объект исследования:

Задачи на множества различных элементов (чисел и других объектов)

Предмет исследования:

Множества и действия с ними.

Методы исследования:

1) Наблюдение;

2) Анализ решения готовых задач;

3) Решение задач, применяя арифметический метод и круги Эйлера;

4) Анкетирование.

Гипотеза:

Применение кругов Эйлера позволяет решать задачи, которые

обычным путём разрешимы лишь при составлении системы нескольких

уравнений с несколькими неизвестными

Немного истории

Леона́рд Э́йлер — швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук (а также физики, астрономии и ряда прикладных наук). Эйлер — автор более чем 850 работ (включая два десятка фундаментальных монографий) по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям. Академик Петербургской, Берлинской, Туринской, Лиссабонской и Базельской академий наук, иностранный член Парижской академии наук. Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. В 1726 году он был приглашён работать в Санкт-Петербург, куда переехал годом позже. С 1726 по 1741, а также с 1766 года был академиком Петербургской академии наук (будучи сначала адъюнктом, а с1731 года — профессором); в 1741—1766 годах работал в Берлине (оставаясь одновременно почётным членом Петербургской академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С. К. Котельников) и астрономы (С. Я. Румовский) были учениками Эйлера. Некоторые из его потомков до сих пор живут в России.

Теоретические основы о кругах Эйлера

Эйлеровы круги (круги Эйлера) — это принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов. Обозначение отношений между объемами понятий посредством кругов было применено еще представителем афинской неоплатоновской школы — Филопоном (VI в.), написавшим комментарии на «Первую Аналитику» Аристотеля. Условно принято, что круг наглядно изображает объем одного какого-нибудь понятия. Объем же понятия отображает совокупность предметов того или иного класса предметов. Поэтому каждый предмет класса предметов можно изобразить посредством точки, помещенной внутри круга. Группа предметов, составляющая вид данного класса предметов, изображается в виде меньшего круга, нарисованного внутри большего круга. Такое именно отношение существует между объемами понятий «небесное тело» (А) и «комета» (B). Объему понятия «небесное тело» соответствует больший круг, а объему понятия «комета» — меньший круг. Это означает, что все кометы являются небесными телами. Весь объем понятия «комета» входит в объем понятия «небесное тело». В тех случаях, когда объемы двух понятий совпадают только частично, отношение между объемами таких понятий изображается посредством двух перекрещивающихся кругов. Такое именно отношение существует между объемом понятий «студент» и «спортсмен». Некоторые (но не все) студенты являются спортсменами; некоторые (но не все) спортсмены являются студентами. Незаштрихованная часть круга А отображает ту часть объема понятия «студент», которая не совпадает с объемом понятия «спортсмен»; незаштрихованная часть круга B отображает ту часть объема понятия «спортсмен», которая не совпадает с объемом понятия «студент». 3аштрихованиая часть, являющаяся общей для обоих кругов, обозначает студентов, являющихся спортсменами, и спортсменов, являющихся студентами. Другой пример пересекающихся множеств. Пусть множество А – это ребята из нашего класса, которые зарегистрированы в социальной сети ВКонтакте.ru и множество В ребят, которые пользуются другой сетью – Facebook. Есть ребята, которые пользуются одновременно двумя сетями – это множество А и В. Данное множество образуется пересечением (общей частью) двух или более множеств. Когда же ни один предмет, отображенный в объеме понятия A, не может одновременно отображаться в объеме понятия B, то в таком случае отношение между объемами понятий изображается посредством двух кругов, нарисованных один вне другого. Ни одна точка, лежащая на поверхности одного круга, не может оказаться на поверхности другого круга Такое именно отношение существует, например, между понятиями «тупоугольный треугольник» и «остроугольный треугольник». В объеме понятия «тупоугольный треугольник» не отображается ни один остроугольный треугольник, а в объеме понятия «остроугольный треугольник» не отображается ни один тупоугольный треугольник. Отношения между равнозначащими понятиями, объемы которых совпадают, отображаются наглядно посредством одного круга, на поверхности которого написаны две буквы, обозначающие два понятия, имеющие один и тот же объем. Такое отношение существует, например, между понятиями "автор и композитор песни "Пять причин" и исполнитель песни "Пять причин". Объемы этих понятий одинаковы, в них отобразилось одно и то же известное лицо — российский композитор и певец Игорь Николаев. Нередко бывает и так: одному понятию (родовому) подчиняется сразу несколько видовых понятий, которые в таком случае называются соподчиненными. Отношение между такими понятиями изображается наглядно посредством одного большого круга и нескольких кругов меньшего размера, которые нарисованы на поверхности большего круга. Такое именно отношение существует между понятиями «скрипка», «флейта», «пианино», «рояль», «барабан». Эти понятия в равной мере подчинены одному общему родовому понятию «музыкальные инструменты». Круги, изображающие соподчиненные понятия, не должны касаться друг друга и перекрещиваться, так как объемы соподчиненных понятий несовместимы; в содержании соподчиненных понятий имеются, наряду с общими, различающие признаки. Эта схема отображает общее, что характерно для отношения любых соподчиненных понятий, взятых из различных областей знания. Это применимо к понятиям: «дом», «сарай», «ангар», «театр», подчиненных понятию «постройка»; к понятиям: «муха», «комар», «бабочка», «жук», «пчела», подчиненных понятию «насекомое» и т. д.

Типы кругов Эйлера

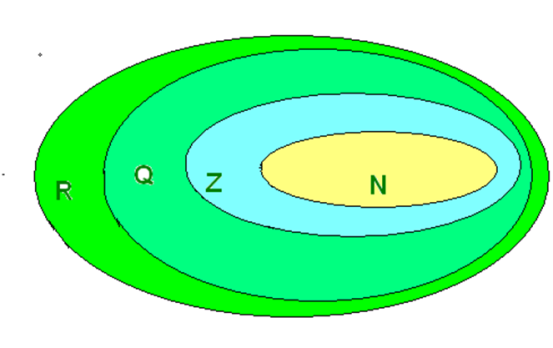
Множество всех действительных чисел изображено с помощью кругов Эйлера.

N - Множество натуральных чисел,

Z – множество целых чисел,

Q – множество рациональных чисел,

R – множество всех действительных чисел.

Зачем нужны круги Эйлера?

Круги Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, менеджменте и не только. Если говорить о видах кругов Эйлера, то можно разделить их на те, что описывают объединение каких-то понятий (например, соотношение рода и вида) – мы их рассмотрели на примере в начале работы. А также на те, что описывают пересечение множеств по какому-то признаку. Таким принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных в интернете мемов. Вот вам один из примеров таких кругов Эйлера:

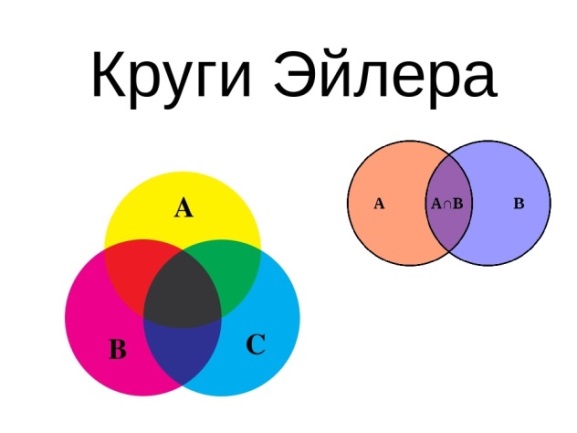
А теперь рассмотрим некоторые задачи:

Задача №1

Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг?

Р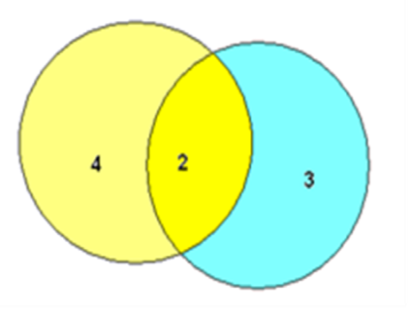 ешение

Изобразим два круга, так как у нас два вида цветов. В одном будем фиксировать владелиц кактусов, в другом — фиалок. Поскольку у некоторых подруг есть и те, и другие цветы, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как кактусы и фиалки у двоих. В оставшейся части «кактусового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «фиалкового» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 подруг.

Ответ. 9 подруг.

З адача №2

В классе 25 учащихся. Из них 5 человек не умеют играть ни в шашки, ни в шахматы. 18 учащихся умеют играть в шашки, 20 — в шахматы. Сколько учащихся класса играют и в шашки, и в шахматы?

Решение

25-5=20 – чел. умеют играть

20+18-20=18 – чел играют и в шашки, и в шахматы .

Задача №3

В классе 38 человек. Из них 16 играют в баскетбол, 17 – в хоккей, 18 – в волейбол. Увлекаются двумя видами спорта - баскетболом и хоккеем – четверо, баскетболом и волейболом – трое, волейболом и хоккеем – пятеро. Трое не увлекаются ни баскетболом, ни волейболом, ни хоккеем.

Сколько ребят увлекается одновременно тремя видами спорта?

С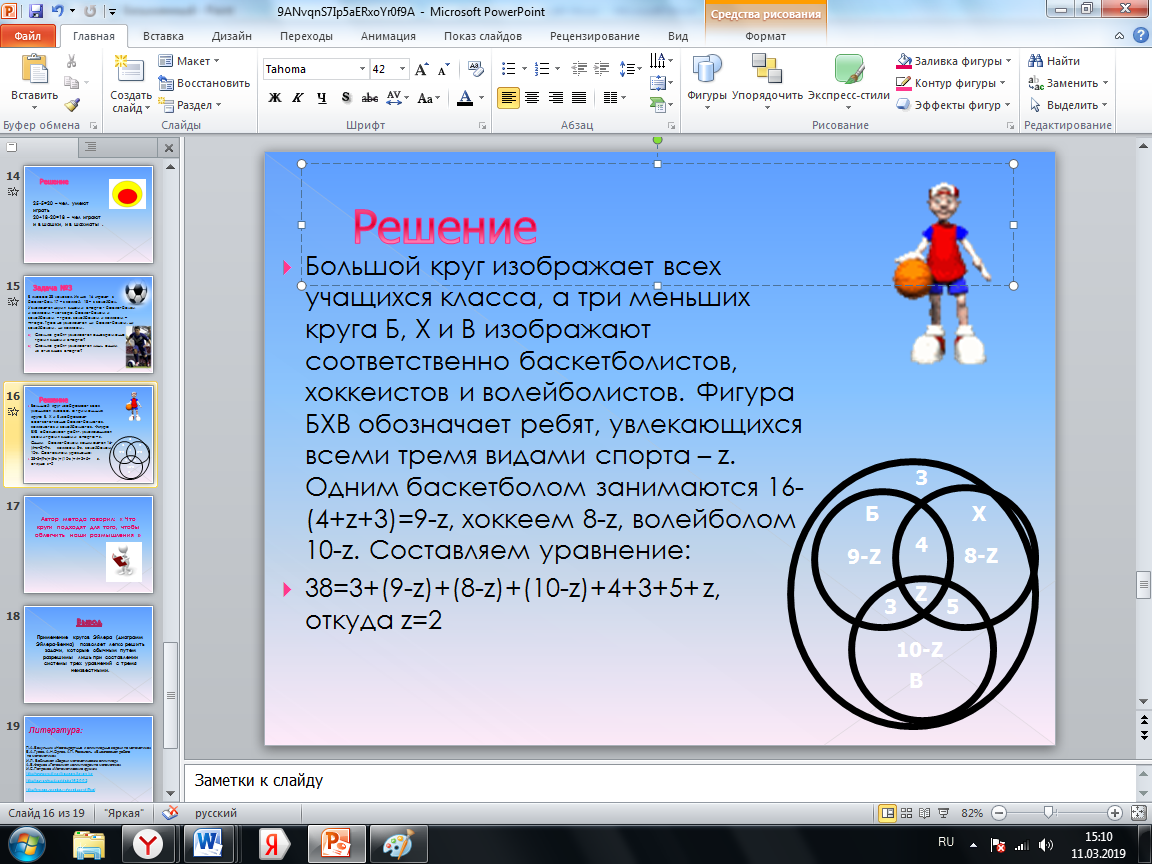 колько ребят увлекается лишь одним из этих видов спорта?

Решение

Всего – 38 - 3

Б – 16

4

Х – 17 3

5

В – 18

1. Z (БХВ) - ?

2. Б; Х; В -?

Большой круг изображает всех учащихся класса, а три меньших круга Б, Х и В изображают соответственно баскетболистов, хоккеистов и волейболистов. Фигура БХВ обозначает ребят, увлекающихся всеми тремя видами спорта – z. Одним баскетболом занимаются 16-(4+z+3)=9-z, хоккеем 8-z, волейболом 10-z. Составляем уравнение:

38=3+(9-z)+(8-z)+(10-z)+4+3+5+ z,

откуда z=2

Задача 4.

Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах, созданных киностудией "Мельница". В частности, вопросы были о мультфильмах, повествующих о приключениях трёх самых известных богатырей - Алёши Поповича, Добрыни Никитича и Ильи Муромца.

Оказалось, что большинству из них нравятся "Три богатыря и Шамаханская царица", "Три богатыря на дальних берегах" и "Три богатыря. Ход конём". В анкетировании принимали участие 38 учеников. Мультфильм "Три богатыря на дальних берегах, нравится 21 ученику. Причем трем среди них нравятся еще и "Три богатыря. Ход конём", шестерым - "Три богатыря и Шамаханская царица. ", а один ребенок одинаково любит все три мультфильма. У мультфильма "Три богатыря. Ход конём" 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким шестиклассникам нравится мультфильм "Три богатыря и Шамаханская царица".

Решение.

Так как по условиям задачи у нас даны три множества, чертим три круга. А так как по ответам ребят выходит, что множества пересекаются друг с другом, чертеж будет выглядеть так:

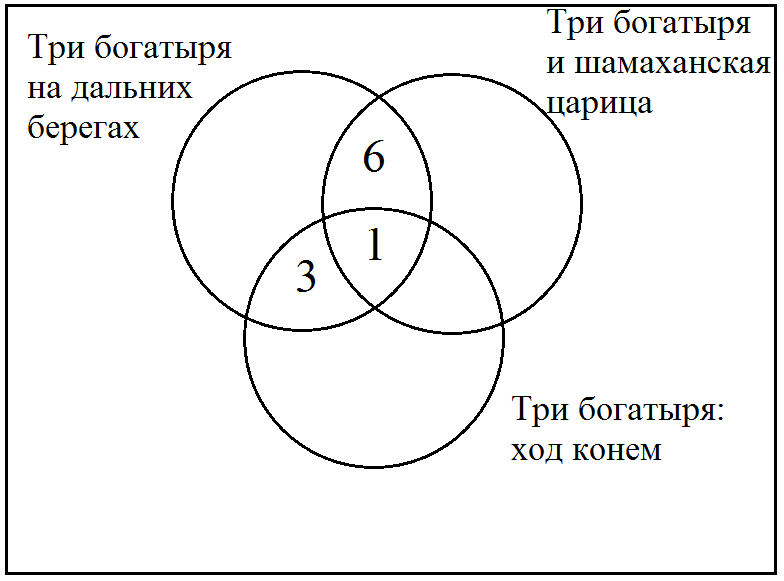в сего – 38 учеников

Ш.Ц. - ?

6

Д.Б. – 21 1 ?

3

Х.К. – 13

Мы помним, что по условиям задачи среди фанатов мультфильма "Три богатыря. Ход конём" пятеро ребят выбрали два мультфильма сразу

В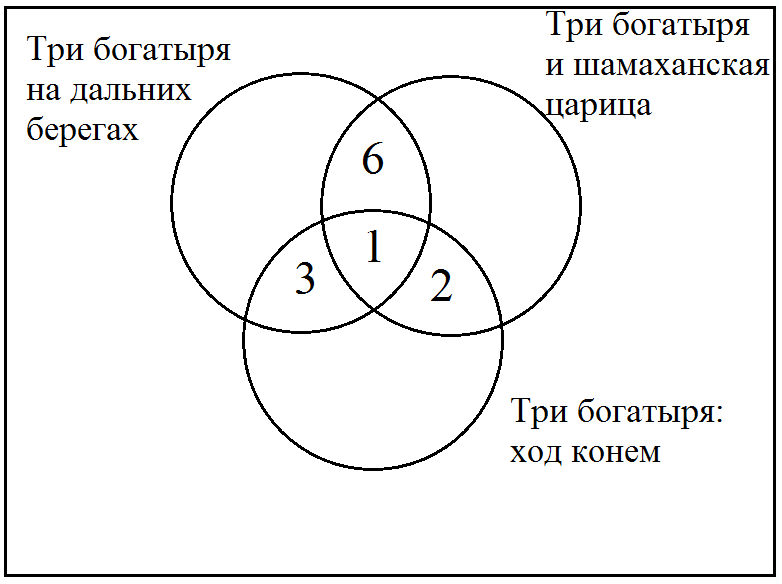 ыходит, что:

21 – 3 – 6 – 1 = 11 – ребят выбрали только "Три богатыря на дальних берегах"

13 – 3 – 1 – 2 = 7 – ребят в последнее время смотрят только "Три богатыря: Ход конём"

Осталось только разобраться, сколько шестиклассников двум другим вариантам предпочитает мультфильм "Три богатыря и Шамаханская царица".

О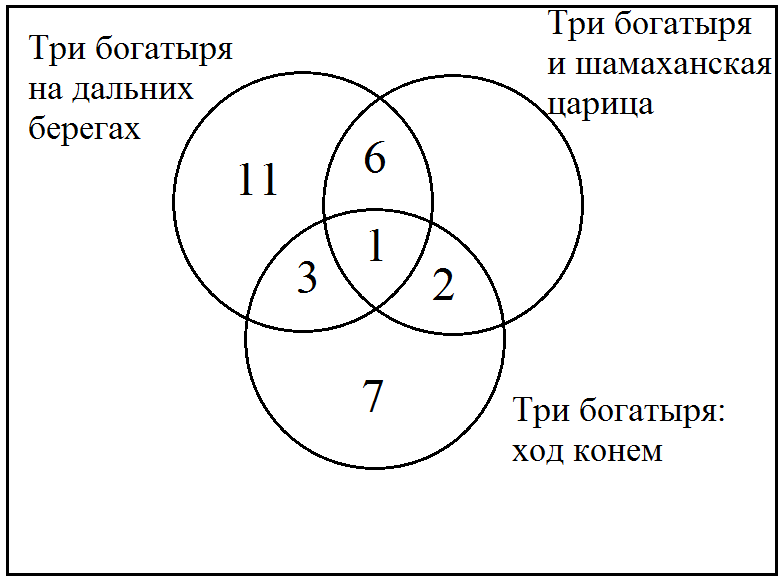 т всего количества учеников отнимаем всех тех, кто любит два других мультфильма или выбрал несколько вариантов:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только "Три богатыря и Шамаханская царица" (Иллюстрация 13 г).

Теперь смело можем сложить все полученные цифры и выяснить, что:

м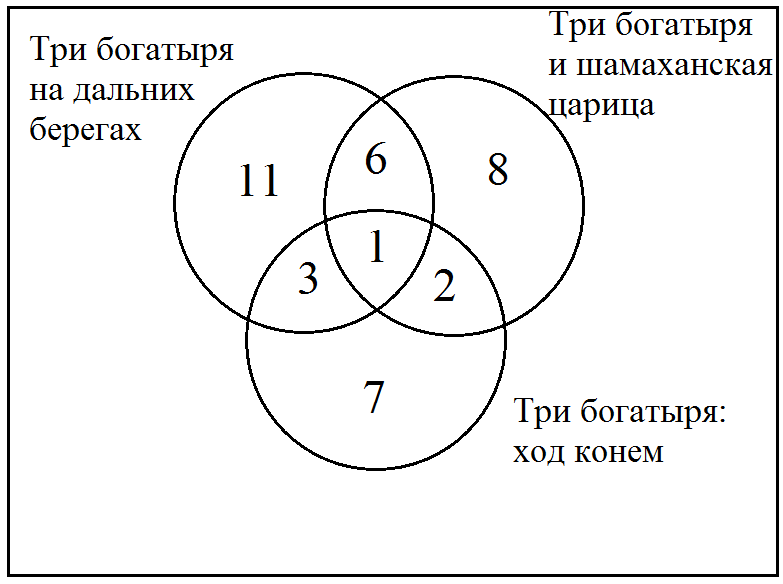 ультфильм "Три богатыря и Шамаханская царица".

выбрали 8 + 2 + 1 + 6 = 17 человек. Это и есть ответ на поставленный в задаче вопрос.

Ответ: 17 человек.

Задача 5.

В некотором городе 85% жителей знают немецкий язык,75% знают русский язык. Сколько % жителей знают оба языка.

Решение:

Выразим условие задачи графически. Обозначим кругом №1 тех, кто знает немецкий язык, кругом №2 – тех, кто знает русский язык.

100-85=15% не знает немецкий язык, запишем число 15 в круг №2.

100-75=25% не знает русский язык, запишем число 25 в круг № 1.

Знают только 1 язык 25+15=40%, тогда знают оба языка 100-40=60%.

Ответ: 60%.

Задача 6.

Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3.Сколько туристов не владеют ни одним иностранным языком?

Решение:

Выразим условие задачи графически. Обозначим кругом №1 тех, кто знает английский, кругом №2 – тех, кто знает французский, и кругом №3 – тех, кто знают немецкий.

Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3.

Английским и французским языками владеют 10 человек, а 3 из них владеют ещё и немецким. Значит, английским и французским владеют 10-3=7 человек

В общую часть английского и французского кругов вписываем цифру 7.

Английским и немецким языками владеют 8 человек, а 3 из них владеют ещё и французским. Значит, английским и немецким владеют 8-3=5 человек.

В общую часть английского и немецкого кругов вписываем число 5.

Немецким и французским языками владеют 5 человек, а 3 из них владеют ещё и английским. Значит, немецким и французским владеют 5-3=2 человека.

В общую часть немецкого и французского кругов вписываем цифру 2.

Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из них владеют и другими языками, значит, только немецкий знают 20 человек.

Английский язык знают 28 человек, но 5+3+7=15 человек владеют и другими языками, значит, только английский знают 13 человек.

Французский язык знают 42 человека, но 2+3+7=12 человек владеют и другими языками, значит, только французский знают 30 человек.

По условию задачи всего 100 туристов. 20+30+13 +5+2+3+7=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним иностранным языком.

Ответ: 20 человек.

Задача 7.

100 шестиклассников нашей школы участвовали в опросе, в ходе которого выяснялось, какие компьютерные игры им нравятся больше: симуляторы, квесты или стратегии. В результате 20 опрошенных назвали симуляторы, 28 — квесты, 12 — стратегии. Выяснилось, что 13 школьников отдают одинаковое предпочтение симуляторам и квестам, 6 учеников — симуляторам и стратегиям, 4 ученика — квестам и стратегиям, а 9 ребят совершенно равнодушны к названным компьютерным играм. Некоторые из школьников ответили, что одинаково увлекаются и симуляторами, и квестами, и стратегиями.Сколько школьников одинаково увлекаются и симуляторами, и квестами, и стратегиями?

Решение:

Выразим условия задачи графически. Обозначим кругом №1 тех, кто увлекается симуляторами, кругом №2 – тех, кто увлекается квестами, и кругом №3 – тех, кто увлекается стратегиями.

Так как 9 ребят совершенно равнодушны к названным компьютерным играм, то только 100-9=91 шестиклассник увлекаются какими-либо играми.

20 опрошенных назвали симуляторы, значит в круг №1 впишем число 20.

28 шестиклассников назвали квесты, значит в круг №2 впишем число 28.

12 человек назвали стратегии, значит в круг №3 впишем число 12.

13 школьников отдают одинаковое предпочтение симуляторам и квестам, тогда в их общую часть впишем число 13.

6 учеников отдают одинаковое предпочтение симуляторам и стратегиям, тогда в их общую часть впишем число 6.

4 школьника отдают одинаковое предпочтение квестам и стратегиям, тогда в их общую часть впишем число4.

Тогда все три вида игры назвали 91-20-28-12-4-6-13=8.

Ответ: 8 школьников одинаково увлекаются и симуляторами, и квестами, и стратегиями.

Задача 8.

В классе 36 учеников. Многие из них посещают кружки: физический кружок посещают 14 человек, математический кружок посещают 18 человек, химический кружок посещают 10 человек. Кроме того, известно, что 2 человека посещают все три кружка; из тех, кто посещает два кружка, 8 человек занимаются в математическом и физическом кружках, 5 — в математическом и химическом, 3 — в физическом и химическом. Сколько человек не посещают никаких кружков?

Решение:

Выразим условия задачи графически. Обозначим кругом №1 тех, кто посещают физический кружок, кругом №2 – тех, кто посещает математический кружок, и кругом №3 – тех, кто посещает химический кружок.

Все 3 кружка посещают 2 человека, значит в общую часть всех кружков впишем число 2.

8 человек занимаются в математическом и физическом кружках, значит в общую часть математического и физического кругов и вписываем число 8.

5 человек занимаются в математическом и химическом кружках, значит в их общую часть вписываем число 5.

3 человека занимаются в физическом и химическом кружках, значит в их общую часть вписываем число 3.

Только физический кружок посещают 14-8-3-2=1 человек, значит в круг №1 впишем число1.

Только в математическом кружке занимаются 18-8-5-2=3 человека, значит в круг №2 впишем число 3.

Только в химическом кружке занимаются 10-5-3-2=0 человек, значит в круг №3 впишем число 0.

В кружках занимается 1+8+3+3+2+5+0=22 человека.

Так как в классе 36 человек, то не посещают никакие кружки 36-22=14 человек.

Ответ: 14 человек.

Задача 9.

У ребят из одной школы спрашивали об их домашних животных. 100 из них ответили, что у них дома есть собака и/или кошка. У 87 ребят была одна собака, а у 63 ребят – одна кошка. У скольких ребят есть и собака и кошка?

Решение:

Чтобы решить эту задачу, не используя круги Эйлера нужно подсчитать, сколько собак и кошек было у учеников. Для этого нужно сложить 87 и 63. 87+63=150 домашних животных. Учеников было всего лишь 100, а дробного числа домашних животных получиться не может. Значит если у каждого ученика 1 домашнее животное, остается еще 50 лишних.

Следовательно, у 50 учеников 2 домашних животных. И так как в задаче указано, что ни у одного из учеников нет 2 кошек или 2 собак, то это значит, что у 50 учеников есть и кошка и собака.

Но этот способ долгий и подходит только для простых задач. Такую задачу намного удобнее решить через круги Эйлера.

Красным кругом изобразим множество обладателей собак, а синим множество обладателей кошек. Всего учеников было 100. Тех, у кого есть и кошка, и собака Х. Чтобы найти количество учеников, у которых только собака нужно из 87 вычесть Х.

Так как всего учеников 100, мы получаем:

87-Х+63=100 Х=150-100 Х=50 учеников

Ответ: у 50 учеников есть и кошка и собака

Задача 10.

Однажды учеников спросили, кто из них любит математику, кому нравится русский язык, а кому физика. Оказалось, что из 36 учеников 2 не любят ни математику, ни русский, ни физику. Математика нравится 25 ученикам, русский язык- 11, физика – 17 ученикам; и математика, и русский- 6; и математика, и физика- 10; русский язык и физика - 4. Сколько человек любят все три предмета?

Решение:

6 человек любят и русский и математику.

Из них X человек любят еще и физику.

Значит, только математику и русский любят 6-Х человек. Только математику и физику 10-Х, только русский и физику 4-Х человек. 25 человек любят математику. Но Х, 6-Х, 10-Х человек любят и другие предметы. Значит, только математику любят 25-(6-Х)-(10-Х)Х= 25-6+Х-10+Х -Х=5+Х человек. Только русский любят 11-(6-Х)-(4-Х)-Х= 11-10+2Х-Х=1+Х учеников, только физику 17-(10-Х) –(4-Х)-Х= 17-14+2Х-Х= 3+Х.

Так как 2 человека не любят ни один из этих предметов, то:

3+Х+9+Х+1+Х+6-Х+10-Х+4-Х+Х=36-2 33+Х=34 Х=1

Ответ: 1 человек любит все три предмета

Задача 11.

В пришкольном лагере "Солнышко" 70 ребят. Из них 27 занимаются в художественном кружке, 32 поют в хоре, 22 увлекаются спортом. В художественном кружке 10 ребят из хора, в хоре 6 спортсменов, в художественном кружке 8 спортсменов; 3 спортсмена посещают и художественный кружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в художественном кружке? Сколько ребят заняты только спортом?

Решение:

Начнем с того, что изобразим на рисунке круги Эйлера подобно тому, как это было сделано в предыдущей задаче. В большом круге, изображающем всех ребят, поместим три меньших круга Р, Х и С, изображающих художественный кружок, хор и спортсменов. Удобно перевести задачу на язык теории множеств. Основным множеством данной задачи является множество всех детей лагеря. Оно состоит из 70 элементов. художественный кружок образует подмножество Р, состоящее из 27 элементов. Хор образует подмножество Х из 32 элементов, и спортсмены образуют подмножество С из 22 элементов. Те ребята художественного кружка, которые поют в хоре, образуют подмножество РХ, являющееся пересечением множеств Р и Х и содержащее по условию 10 элементов. Трое из этих десяти еще и спортсмены, т. е. образуют подмножество РХС, содержащее 3 элемента. Остальные семеро из десяти спортом не увлекаются и образуют множество РХС^’ из семи элементов (штрих над буквой означает подмножество соответствующего множества). Точно так же найдем, что множество РСХ^’ спортсменов драмкружка, не поющих в хоре, содержит 8 – 3 = 5 элементов, а множество СХР^’ поющих спортсменов, не посещающих драмкружок, составлено из 6 – 3 = 3 элементов.

Мы видим, что 5 + 3 + 3 = 11 спортсменов посещают хор или художественный кружок. Остальные 22 – 11 = 11 увлекаются только спортом, они образуют подмножество СР^’Х^’. Аналогично этому находим число элементов подмножества РС^’Х^’, оно равно 12, и число э лементов подмножества ХР^’С^’, оно оказалось равным 19 элементам. Вычитая из общего числа элементов множества 70 сумму подчёркнутых чисел, равную числу элементов объединения множеств Р, Х и С, найдем, что число элементов множества Х^‘Р^‘С^‘ равно 10, т. е. 10 ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке.

С

22 – 5 – 3 – 3 = 11

8 – 3 = 5 6 – 3 = 3

РХС

3

Р Х

12 10 – 3 = 7 19

Задача 12.

В нашей школе 647 ученика. Из них посещают кружки эстетического и познавательного направления 214 учащихся, кружки спортивно технического направления 346 учащихся, не посещают никакие — 87 человек. Сколько учащихся совмещают эти два направления?

Решение. 

Решим её с помощью кругов Эйлера. В большой круг поместим всех учащихся, в него два круга с эстетическим направлением — Э и спортивным — С, оставшихся учащихся оставим за этими двумя. Тогда задача будет решаться следующим образом: 647 – 87 = 560 — это множество СЭ, 560 – 346 = 214 — это «эстеты» не посещающие кружки спортивно технического направления, т. е. С^’. Теперь 346 – 214 = 32 учащихся совмещают оба направления.

ЭС

346-214=

32

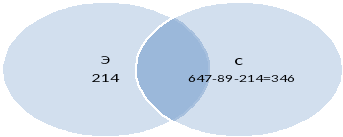
Ответ: 32 ученика

Выводы.

1) Таким образом, существует целый класс задач, которые решаются с помощью кругов Эйлера. Алгоритм решения состоит из следующих этапов:

• Записываем краткое условие задачи.

• Выполняем рисунок.

• Записываем данные в круги Эйлера.

• Выбираем условие, которое содержит больше свойств.

• Анализируем, рассуждаем, не забывая записывать результаты в части круга

• Записываем ответ.

Я полагаю, что не стоит сомневаться в полезности данного способа решения задач, так как его наглядность упрощает и облегчает путь к их решению. С помощью кругов Эйлера мне уже приходилось решать задачи на школьной математической олимпиаде, а так же этот способ очень облегчил подсчёт организатора школы при подведении итогов занятости учащихся школы во внеурочное время. Данный способ, безусловно, расширяет математический кругозор, обогащает арсенал средств, используемых в решении разнообразных задач, повышает интерес к математике.

Автор метода говорил: « Что круги подходят для того, чтобы облегчить наши размышления »

Вывод

Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.

Иллюстрация13.

а ) б)

в ) г)

15