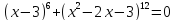Министерство образования и науки Республики Бурятия
Муниципальное образование «Закаменский район»
Муниципальное учреждение «Закаменское районное управление образования»
Муниципальное автономное образовательное учреждение
«Средняя общеобразовательная школа №5 г.Закаменск»
Районная научно-практическая конференция «Шаг в будущее»
Секция «Алгебра»
Метод мажорант
Выполнила: Злыгостева Виктория
Ученица 10 «б» класса
Руководитель: Дашеева С.С.
Г. Закаменск
2016год
Содержание:
Введение
1. Определение мажоранты функции
2. Метод мажорант
3. Примеры решения уравнений и неравенств методом мажорант
Заключение
Список использованной литературы
Введение
Одной из важных задач математической науки является решение уравнений и неравенств. Изучение математики невозможно без умения решать разнообразные неравенства и уравнения, поэтому я решила изучить один из способов решения неравенств и уравнений – метод мажорант. При решении нестандартных задач встречаются уравнения, содержащие разнородные функции. Задания подобного типа встречаются среди экзаменационных. В учебнике «Алгебра и начала анализа» А.Г.Мордковича есть несколько подобных заданий, но четкого определения и метода решения данных уравнений нет.
В разных источниках данный метод называется по-разному. Некоторые математики называют этот метод по-другому: «метод математической оценки», «метод mini-max», задачи «встреча на краю». А.Г.Мордкович в учебнике «Алгебра и начала анализа» предлагает рассматривать данный метод как «довольно красивую разновидность функционально-графического метода». Но в большинстве источников он называется «метод мажорант» Это очень красивый метод, и ему непременно надо научиться всем.
Этим методом можно решать нестандартные уравнения, уравнения повышенной сложности, например, уравнения в левой и правой части которого находятся функции, имеющие различную природу, уравнения или системы уравнений, в которых количество переменных превышает количество уравнений, задачи с параметрами. Метод мажорант также называют методом оценки левой и правой частей, входящих в уравнения и неравенства. Применение метода оценок будет успешным, если знать, как находить экстремумы элементарных функций, область значений, исследовать функцию с помощью производной.
Цели:
Изучить определение мажоранты функции и исследовать, какие функции имеют мажоранту;
Изучить метод мажорант и его применение для решения нестандартных уравнений и неравенств;
Привести примеры уравнений и неравенств, которые могут быть решены методом мажорант.
Актуальность работы заключается в том, что данный метод позволяет успешно решать олимпиадные задачи, конкурсные задачи, уравнения повышенной сложности, например, уравнения части С ЕГЭ по математике.
Определение мажоранты функции.
Определение. Мажорантой данной функции f(х) на множестве Р называется такое число М, что либо f(х) ≤ М для всех х ϵ Р, либо f(х) ≥ М для всех х ϵ Р
Термин «мажоранта» происходит от французского слова «majorante», от «majorer» — объявлять большим.
Мажоранты многих элементарных функции известны. Их нетрудно указать, зная область значений функции. Приведем примеры функций, мажоранты которых хорошо знаем.
Метод мажорант основан на том, что множество значений некоторых функций ограничено. При использовании метода мажорант мы выявляем точки ограниченности функции, то есть в каких пределах изменяется данная функция, а затем используем эту информацию для решения уравнения или неравенства.
Чтобы успешно пользоваться этим методом, нужно хорошо знать, какие функции имеют ограниченное множество значений.
Приведем примеры элементарных функций, которые имеют ограниченное множество значений: 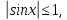
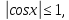
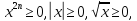
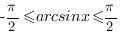

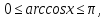
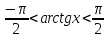 ,
, 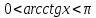

Мажоранты некоторых функции можно найти, используя следующие полезные неравенства:
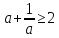 , при а 0 и
, при а 0 и 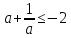 , при а
, при а
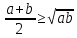 ,
,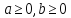 , причем равенство достигается при
, причем равенство достигается при 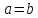 .
.
3. 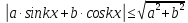
Метод мажорант.
Основная идея метода мажорант может быть сформулирована в виде следующих теорем:
Теорема №1.
Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) ограничена на этом множестве числом А сверху, а g(x) ограничена на этом множестве тем же числом А, но снизу.
Тогда уравнение f(x) = g(x) равносильно системе: 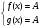

Теорема №2.
Пусть f(x) и g(x) – некоторые функции, определённые на множестве D. Пусть f(x) и g(x) ограничены на этом множестве снизу (сверху) числами А и В соответственно. Тогда уравнение f(x) + g(x) = А+В равносильно системе уравнений: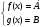
Теорема №3.
Пусть f(x) и g(x) – некоторые неотрицательные функции, определённые на множестве D. Пусть f(x) и g(x) ограничены сверху ( или снизу) числами А и В соответственно. Тогда уравнение f(x)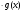 = А
= А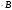 равносильно системе уравнений
равносильно системе уравнений
(при условии, что А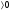 и В
и В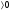 :
: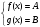
В этом утверждении особенно важно условие неотрицательности функций f(x) и g(x), а также условие положительности А и В.
Рассмотрим примеры решения уравнений и неравенств методом мажорант.
Примеры решения уравнений и неравенств методом мажорант
Пример 1. Решите уравнение: 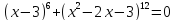
Решение:
Чтобы решить это уравнение мы не будем возводить двучлен в шестую степень и трехчлен в двенадцатую.
Заметим, что 6 и 12 – четные числа, следовательно,
 при любом значении х
при любом значении х
и  при любом значении х.
при любом значении х.
Равенство возможно, если одновременно  и
и 
Корень первого уравнения  ,
,
корни второго уравнения  и
и  . Число
. Число является корнем обоих уравнений, его мы и запишем в ответ.
является корнем обоих уравнений, его мы и запишем в ответ.
Ответ: 3
Пример 2. Решить уравнение: .
Решение:
Преобразуем уравнение: .
Оценим значение выражения, стоящего в правой части уравнения:
, , .
Оценим значение выражения, стоящего в левой части уравнения:
.
Тогда ,  .
.
Таким образом, равенство возможно, если
Решим уравнение (1).






Проверим, что  является решением уравнения (2):
является решением уравнения (2):
Следовательно,  является решением системы уравнений (1) и (2), а, значит, и решением данного уравнения.
является решением системы уравнений (1) и (2), а, значит, и решением данного уравнения.
Ответ: .
.
Пример 3. Решить уравнение: .
Решение:
Оценим значение выражения, стоящего в левой части уравнения:  .
.
Оценим значение выражения, стоящего в правой части уравнения:
.
,  .
.
Таким образом, равенство возможно, если
Решим уравнение (2).



Проверим, что  является решением уравнения (1):
является решением уравнения (1):
Следовательно, является решением системы уравнений (1) и (2), а, значит, и решением данного уравнения.
является решением системы уравнений (1) и (2), а, значит, и решением данного уравнения.
Ответ: 3.
Пример 4. Решить систему уравнений
Решение:
Оценим первое уравнение системы: tg2 x + ctg2 x ≥ 2 при
2cos2 y ≤ 2. Следовательно, первое уравнение равносильно системе
Сама система примет вид: 
Ответ:
Пример 5.
Решите уравнение:
Решение:
Оценим множители левой части уравнения: 





перемножив почленно эти неравенства получим:
Тогда левая часть уравнения равна правой, лишь при условии:


 одновременно.
одновременно.
Данное уравнение равносильно системе уравнений
Ответ:
Пример 6. Решить уравнение: =6
Решение:
Значения первого арифметического квадратного корня больше или равны 1, причём равно 1, только в случае, если верно равенство
 =0. Аналогично, значения второго арифметического квадратного корня не меньше 5 (больше или равны 5).
=0. Аналогично, значения второго арифметического квадратного корня не меньше 5 (больше или равны 5).
Следовательно, согласно методу мажорант, левая часть уравнения имеет минимум, равный 6, а правая часть представляет собой постоянную функцию со значением 6.
Но чтобы значения функций совпали, надо проверить, имеет ли решение система:
Единственное решение этой системы (4;3)
Ответ: (4;3)
Заключение
В данном исследовании, во-первых, я узнала совершенно новый для себя способ решения уравнений-метод мажоранта, который встречается в ЕГЭ и мало изучается в школе. Во-вторых, научилась применять его непосредственно при решении уравнений и неравенств. Я изучила и проанализировала материал по данной теме, на конкретных примерах научилась применять метод мажоранта при решении уравнений и неравенств.
Список литературы:
Мордкович А. Г. «Алгебра и начала математического анализа 10-11», «Мнемозина», Москва 2012.
Куланин Е.Д., Норин В.П. «3000 конкурсных задач по математике», Москва: Aйрис-пресс, 2003.
Балаян Э.Н «1001 олимпиадная и занимательная задачи по математике», Ростов-на-Дону: Феникс, 2008.
Корешкова Т. А., Мирошин В. В.,Шевелёва Н. В. Математика. Тренировочные задания. Москва: Эксмо, 2013.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П., Ивлев Б.М., Шварцбурд С.И. «Алгебра и начала анализа 10-11», Москва: Просвещение, 2008.







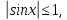
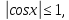
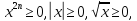
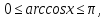
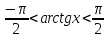 ,
, 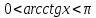
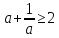 , при а 0 и
, при а 0 и 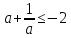 , при а
, при а 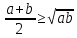 ,
,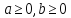 , причем равенство достигается при
, причем равенство достигается при 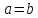 .
.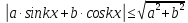
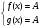

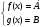
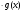 = А
= А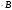 равносильно системе уравнений
равносильно системе уравнений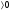 и В
и В