Исследовательская работа МШНОУ по теме "Практическое применение теоремы Пифагора".

Муниципальное автономное образовательное учреждение

средняя школа №10 города Володарска

Нижегородской области

Научно – исследовательская работа

по математике

«Практическое применение теоремы Пифагора»

Выполнили: Перепёлкина Алёна, ученица 8 класса

Руководитель:

Богданова Мария Дмитриевна

учитель математики

г. Володарск

Пояснительная записка

«Геометрия владеет двумя сокровищами:

одно из них – это теорема Пифагора» Иоганн Кеплер

Актуальность: по выражению известного ученого Иоганна Кеплера, «геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и е сли первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…».

Теорема Пифагора – одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что с ее помощью можно вывести большинство теорем геометрии.

Один американский математик, наш современник, около 20 лет собирал различные способы доказательства теоремы Пифагора, и сейчас его «коллекция» содержит около 300 различных доказательств. Это говорит о том, что древняя теорема актуальна и интересна людям до сих пор.

Новизна: в школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. К сожалению, вопрос о практическом применении теоремы Пифагора не рассматривается.

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

Объект исследования: теорема Пифагора.

Предмет исследования: различные интерпретации и способы доказательства теоремы Пифагора, ее применение при решении практических задач.

Изучая дополнительную литературу по выбранной теме, были выдвинуты гипотезы:

1)существуют другие интерпретации теоремы Пифагора;

2)теорема Пифагора применяется при решении многих практических задач.

3) За красоту и гармонию в природе «отвечает» математика. То есть, особые числовые

закономерности существуют во всем, что нас окружает.

4) С помощью теоремы Пифагора можно решать не только математические задачи.

Цели исследования:

- внимательно изучив формулировку теоремы Пифагора, проанализировав доказательства и используя обобщение, рассмотреть иные интерпретации теоремы Пифагора;

- выяснить области применения теоремы Пифагора

Для достижения цели были поставлены следующие задачи:

1. Провести анализ истории возникновения теоремы Пифагора и творческой деятельности Пифагора.

2. Исследовать различные способы доказательства и рассмотреть иные интерпретации теоремы Пифагора.

3. Показать практическое применение теоремы Пифагора.

Практическая значимость:

• Использование приобретенных знаний и навыков исследовательской работы при изучении других школьных предметов.

• Расширение и углубление знаний учащихся по данной теме.

• Формирование навыков исследовательской деятельности учащихся.

• Развитие познавательной активности учащихся, повышение интереса к предмету.

• Совершенствование навыков работы с математической литературой.

Умения и навыки:

• Организация и проведение эксперимента.

• Использование специальной литературы.

• Приобретение умения делать обзор собранного материала (доклад, презентацию, реферат).

• Оформление работы рисунками, диаграммами, фотографиями.

• Активное участие в обсуждении своей работы.

Оглавление

I Введение. ……………………………………………………………………………стр.4 – 5

II Основная часть……………………………………………………………………. стр. 6 – 23

1. Немного о Пифагоре………………………………………………………………..стр.6 - 8

2. История возникновения теоремы Пифагора……………………………………стр.8 - 9

3. Различные способы доказательства теоремы Пифагора.. ………………стр.10-15

4. Исторические задачи……………………………………………………………….стр.15-16

5. Теорема Пифагора в

• строительстве и архитектуре…………………………………………………стр.17-19

• мобильной связи………………………………………………………………стр.20

• литературе……………………………………………………………………..стр.20-21

III. Заключение ……………………………………………………………………….стр.22

IV. Литература………………………………………………………………………….стр.23

V. Приложение…………………………………………………………………………стр. 24-28

Приложение №1…………………………………………………………………….стр.24-25

Приложение №2…………………………………………………………………….стр.26

Приложение №3…………………………………………………………………….стр.27-28

I. Введение.

В школьном курсе геометрии с помощью теоремы Пифагора решаются только математические задачи. К сожалению, вопрос о практическом применении теоремы Пифагора не рассматривается.

В связи с этим, целью нашей работы было выяснить области применения теоремы Пифагора.

В настоящее время всеобщее признание получило то, что успех развития многих областей науки и техники зависит от развития различных направлений математики. Важным условием повышения эффективности производства является широкое внедрение математических методов в технику и народное хозяйство, что предполагает создание новых, эффективных методов качественного и количественного исследования, которые позволяют решать задачи, выдвигаемые практикой.

Рассмотрим примеры практического применения теоремы Пифагора. Не будем пытаться привести все примеры использования теоремы - это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой.

Гипотеза:

1) Существуют другие интерпретации теоремы Пифагора;

2) С помощью теоремы Пифагора можно решать многие практические задачи.

По данной исследовательской работе определена следующая цель:

Выяснить области применения теоремы Пифагора.

Исходя из вышеназванной цели, были обозначены следующие задачи:

1. Собрать информацию о практическом применении теоремы Пифагора в различных источниках и определить области применения теоремы.

2. Изучить некоторые исторические сведения о Пифагоре и о его теореме.

3. Показать применение теоремы при решении исторических задач.

4. Провести измерения крыши детского сада «Цыплёнок», решить прикладные задачи по установке ёлки и молниеотвода.

5. Обработать собранные данные по теме.

6. Оформить наработанный материал в виде проекта.

Решению названных задач было посвящено наше исследование, которым мы занимались 3 месяца. Мы занимались поиском и сбором информации – изучали печатный материал, работали с материалом в интернете, обработкой собранными данными. Решали исторические задачи и занимались задачами по исследованию крыши детского сада, расчетом длины молниеотвода и задачей по установке ёлки. Провели анкетирование учащихся, учителей, родителей и обработали результаты. Было опрошено 27 учащихся 8-11 классов, 14 учителей и 15 родителей учащихся 8 класса. Нам интересно знать, знают ли теорему Пифагора ученики, учителя, родители?

И чтобы это выяснить, мы провели опрос учеников с 8-11 классы, учителей, родителей.

Анкета включала в себя вопросы:

1. Как называется самая известная теорема геометрии?

2. Можете ли вы её сформулировать?

Д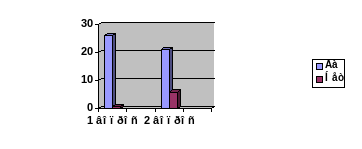 иаграмма №1 Результаты анкетирования учащихся

Диаграмма №2 Результаты анкетирования учителей

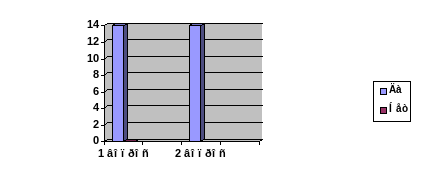
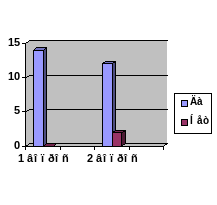
Диаграмма №3 Результаты анкетирования родителей учащихся 8 класса

Для своего исследования мы вначале изучили вопрос о теореме Пифагора по школьным учебникам «Геометрия 7-9» Атанасяна Л.С. и Руденко В.Н., а также по учебнику Погорелова А.В. «Геометрия 7-11». Рассмотрели в данных учебниках задачи по теореме Пифагора.

В Интернете мы ознакомились с практическим применением теоремы и историческими задачами. Вопрос о практическом применении теоремы Пифагора и о самом Пифагоре в школьном учебнике геометрии Л.С. Атанасяна, по которому занимались мы, не освещен. Упоминается лишь немного о биографии Пифагора и о том, как древние египтяне строили прямые углы с помощью веревки, разделенной на 12 равных частей (3,4,5). Это же упоминается и в учебнике геометрии Погорелова А.В. А вот в учебнике геометрии Руденко В.Н. по практическому применению теоремы решаются некоторые интересные задачи, хотя вопрос можно сказать, также не освещен. Вопрос о некоторых исторических сведениях, о Пифагоре и его теореме мы доработали по книгам Волошинова А.В. «Пифагор» и «Математика и искусство». В книге Литцмана В. «Теорема Пифагора» рассматриваются способы доказательства теоремы.

Исследовав литературные источники, мы не нашли в них вопроса о практическом применении теоремы Пифагора. Поэтому самостоятельно изучить этот вопрос нам удалось только в интернете, где мы и выявили некоторые области ее применения.

Нас заинтересовала архитектура с точки зрения применения теоремы Пифагора и мы решили провести исследования крыши детского сада «Цыплёнок», рассмотрели вопрос о возведения молниеотвода на крышу детского сада, а также рассмотрели вопрос об установке новогодней ёлки на площади г. Володарска.

Методика исследования:

1. Изучение теоретического материала (логическая ступень познания).

2. Изучение методик исследования.

3. П рактическое выполнение исследования.

4. Коммуникативный (метод измерения, анкетирование).

5. Метод моделирования (модель установки ёлки, молниеотвода).

6. эмпирический (наблюдение, эксперимент, измерение).

Вид проекта: информационно-исследовательский.

II. Основная часть

1. Немного о Пифагоре

А что мы знаем о Пифагоре? Чем знаменит Пифагор?

А лександр Викторович ВОЛОШИНОВ - кандидат физико-математических наук, доктор философских наук в своей книге «Пифагор» написал: «Пифагор – не только самый популярный ученый, но и самая загадочная личность, человек-символ и человек-фантом, философ и пророк. Основоположник дедуктивного научного знания – математики и родоначальник многих мистических учений, учредитель религиозно-этического братства и создатель научно философской школы, ставшей воистину союзом Истины, Добра и Красоты»

Мы познакомились с биографией самого выдающегося ученого, рассмотрели, в каких жизненных ситуациях встречается теорема Пифагора, проследили связь научных знаний с практической деятельностью человека. Для этого мы провели исследовательскую работу по данной теме.

Крепкого телосложения юношу судьи одной из первых в истории Олимпиад не хотели допускать к спортивным состязаниям, так как он не вышел ростом. Но он не только стал участником Олимпиады, но и победил всех противников. Такова легенда. Этот юноша был Пифагор - знаменитый математик. Вся его жизнь – легенда, точнее наслоение многих легенд. Великий ученый Пифагор родился около 570 г. до н.э. на острове Самос (откуда и пошло прозвище Пифагор Самосский), одном из самых цветущих островов Ионии, у берега Малой Азии, в семье богатого ювелира. Всего 5 километров водной глади отделяло этот остров от большой земли. Отец Пифагора - Мнесарх – резчик по драгоценным камням, мать – Парфениса. Ещё до рождения он был посвящен своими родителями свету Аполлона. Он был очень красив и с детства отличался разумом и справедливостью. С юных лет Пифагор стремился проникнуть в тайны Вечной Природы, постичь смысл Бытия.

Пифагор происходил из аристократической семьи и в детстве получил превосходное по тем временам образование. Однако этих знаний ему показалось недостаточно, и он отправился в трудное и небезопасное путешествие по странам восточной части Средиземного моря, Египту и Вавилону, чтобы постичь премудрости других народов. Совсем юным Пифагор покинул родину. Он прошел по дорогам Египта, 12 лет жил в Вавилоне, где слушал речи жрецов, открывавших перед ним тайны астрономии и астрологии, затем несколько лет – в Италии.

Знания, полученные им в храмах Греции не давали ответов на все волнующие его вопросы, и он отправился в поисках мудрости в Египет. В течение 22 лет он проходил обучение в храмах Мемфиса и получил посвящение высшей степени. Здесь же он глубоко изучил математику, “науку чисел или всемирных принципов”, из которой впоследствии сделал центр своей системы. Из Мемфиса, по приказу вторгшегося в Египет Камбиза, Пифагор вместе с египетскими жрецами попадает в Вавилон, где проводит еще 12 лет. Здесь он имеет возможность изучить многие религии и культы, проникнуть в мистерии древней магии. Уже в зрелом возрасте Пифагор переселяется в Сицилию и там, в Кротоне, создает удивительную школу, которую назовут пифагорейской.

Приблизительно в 530 году Пифагор наконец возвратился в Грецию и вскоре переселился в Южную Италию, в г. Кротон. В Кротоне он основал пифагорейский союз, который был одновременно философской школой, политической партией и религиозным братством. Здесь были соединены философия с жизненной практикой, указывающей человеку достойный путь к судьбе, ожидающей его после смерти. Школа жила общинами со строгой дисциплиной нравов, от учеников требовалось целомудрие и воздержание. Однако, аскетизм не был идеалом пифагорейцев; брак являлся для них священным понятием. В школу, наряду с юношами, принимались и девушки. Обучение было многоступенчатым и далеко не каждому давалось сокровенное знание. Лишь те, кто успешно прошёл все испытания, допускался во внутренний двор дома Учителя. Здесь Пифагор наставлял своих ближайших учеников. Строгий образ жизни пифагорейцев, их созерцательная философия, благожелательность к человеку и стремление делать добро, оказать помощь, привлекали к ним многих людей. Союз вскоре стал центром политической и духовной жизни всего Кротона. Они были трудолюбивы и аскетичны – Пифагор и его ученики. Вот заповеди пифагорейцев.

• Делай лишь то, что впоследствии не огорчит тебя и не принудит раскаиваться.

• Не делай никогда того, что не знаешь, но научись всему, что следует знать.

• Не пренебрегай здоровьем своего тела.

• Приучайся жить просто и без роскоши.

• Прежде чем лечь спать, проанализируй свой поступки за день.

Школа Пифагора дала Греции целую плеяду талантливых философов, физиков и математиков. С их именем связаны в математике систематическое введение доказательств в геометрию, рассмотрение ее как абстрактной науки, создание учения о подобии, доказательство теоремы, носящей имя Пифагора, построение некоторых правильных многоугольников и многогранников, а также учение о четных и нечетных, простых и составных, о фигурных и совершенных числах, арифметических, геометрических и гармонических пропорциях и средних.

Ученики Пифагора расселились по Греции и ее колониям, где организовали школы, в которых преподавали главным образом арифметику и геометрию. Сведения об их достижениях содержатся в сочинениях позднейших ученых – Платона, Аристотеля и других. Учения Пифагора и его учеников охватило гармонию, геометрию, теорию чисел, астрономию. Но более всего пифагорейцы ценили результаты, полученные в теории гармонии, так как они подтверждали их идею, что числа определяют все.

В возрасте 60 лет Пифагор женился на своей ученице Феано, девушке удивительной красоты, покорившей сердце мудрого философа своей чистой и пламенной любовью, безграничной преданностью и верой. Феано дала Пифагору двух сыновей и дочь, все они были верными последователями своего Великого отца. Один из сыновей Пифагора стал впоследствии учителем Эмпидокла и посвятил его в тайны пифагорейского учения. Дочери своей Дано Пифагор доверил хранение своих рукописей. После смерти отца и распада союза Дано жила в величайшей бедности, ей предлагали большие суммы за манускрипты, но верная воле отца, она отказалась отдать их в посторонние руки.

30 лет прожил Пифагор в Кротоне. За это время ему удалось осуществить то, что оставалось мечтою многих посвященных: он создал поверх политической власти мудрую власть высшего знания, подобную древнеегипетскому жречеству. Совет Трехсот, созданный и возглавляемый Пифагором, был регулятором политической жизни Кротона и распространял свое влияние на другие города Греции в течение четверти века. Но ничто так не раздражает посредственность, не вызывает зависть и ненависть, как владычество великого ума. Мятеж против правления аристократической партии, вспыхнувший в Сибарисе, явился началом гонения на пифагорейский союз. Многие из учеников погибли под обломками пылающего здания школы, другие погибли голодной смертью в храмах. О времени и месте смерти самого Пифагора достоверных сведений не сохранилось. Воспоминания о Великом Учителе и его учении было сохранено теми немногими, которым удалось бежать в Грецию. Мы находим его в “Золотых Стихах” Лизия, в комментариях Гераклита, в отрывках Филолая и Архита, а также в “Тимее” Платона. Прекрасная стройная система, данная миру Пифагором никогда не была забыта. Она стала основой метафизики Платона, возродилась в Александрийской школе, в трудах многих позднейших античных философов.

Пифагор – это греческий ученый, религиозный и политический деятель. Трудно сказать, какие научные идеи принадлежали Пифагору, какие – его воспитанникам. Но рассказывают, что Пифагор, доказав свою знаменитую теорему, отблагодарил богов, принеся им в жертву 100 быков. Пифагор не записал своего учения. Оно известно лишь в пересказах Аристотеля и Платона. Греческий ученый Гераклит утверждал, что Пифагор ученее всех современников, однако порицал его за склонность к магии. Дело в том, что числа для пифагорейцев были наполнены магическим содержанием, они преклонялись перед гармонией чисел. Пифагор был не только математиком, но и философом. Ему принадлежит немало великих догадок. Вот почему люди помнят его уже две с половиной тысячи лет, а среди знаменитых олимпийских чемпионов Пифагор наиболее знаменит, - ему выпало счастье победить не только соперника, но и время.

2. История открытия теоремы Пифагора

Теорема Пифагора – самая известная из всех геометрических теорем. О ней писал в своих произведениях римский архитектор и инженер Ветрувий, греческий писатель-моралист Плутарх, греческий ученый III века Диоген Лаэрций, математик V века Прокл и многие другие.

Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:

"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".

В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары.

Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой - на критическом изучении греческих источников, Ван-дер-Варден (голландский математик) сделал следующий вывод:

"Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку."

К антор (крупнейший немецкий историк математики) считает, что равенство 3² + 4² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея)

По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5.

Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Также существует такой факт, что за 1500 лет до Пифагора древние египтяне знали о том, что треугольник со сторонами 3,4 и 5 является прямоугольным, и пользовались этим свойством для построения прямых углов при планировке земельных участков и сооружений зданий.

В связи с указанным способом построение прямого угла треугольник со сторонами 3,4 и 5 единиц называют «египетским».

О том, что теорема «квадрат гипотенузы равен сумме квадратов катетов» восходит к Пифагору, утверждали древнегреческий писатель и историк Плутарх (Iв.) и древнегреческий философ – идеалист Прокл (Vв.).

Долгое время считали, что до Пифагора эта теорема не была известна, и поэтому ее назвали «теоремой Пифагора». С таким названием она и сейчас изучается в курсе планиметрии средней школы.

Однако, известно, что она применялась для решения различных задач задолго до Пифагора древними египтянами, вавилонянами, китайцами, индусами и другими древними народами. В настоящее время установлено, что эта важнейшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора.

В Китае предложение о квадрате гипотенузы было известно по крайней мере за 500 лет до Пифагора. В самом древнем дошедшем до нас китайском математико-астрономическом сочинении «Чжоу-би», написанном примерно за 600 лет до Пифагора, среди других предложений, относящихся к прямоугольному треугольнику, содержится и теорема Пифагора. Еще раньше эта теорема была известна индусам и древним индийцам.

Н есколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, т. е. к 2000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях.

Геометрия у индусов, как и у египтян и вавилонян, была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около 18 века до н. э.

Сохранилась лишь легенда, которая гласит, что, доказав свою теорему, Пифагор принес богам в жертву быка, по другим источникам даже сотню быков.

Другие формулировки теоремы.

У Евклида эта теорема гласит (дословный перевод):

"В прямоугольном треугольнике квадрат стороны, натянутой над прямым углом, равен квадратам на сторонах, заключающих прямой угол".

В Geometria Culmonensis (около 1400 г.) в переводе теорема читается так :

"Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".

Во времена Пифагора формулировка теоремы звучала так: «Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах»

Современная формулировка теоремы гласит:

«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов»

В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифатор первым дал ее полноценное докзательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал". С другой стороны, Прокл утверждает, что доказательство в "Началах" принадлежит самому Евклиду. Как мы видим, история математики почти не сохранила достоверных данных о жизни Пифагора и его математической деятельности. Зато легенда сообщает даже ближайшие обстоятельства, сопровождавшие открытие теоремы. Многим известен сонет Шамиссо.

Ученические шаржи.
Учащиеся средних веков придумывали стишки при изучении теоремы; рисовали шаржи.

Смотрите, а вот и "Пифагоровы штаны во все стороны равны"

3. Различные способы доказательства теоремы Пифагора

Существует более 500 доказательств теоремы Пифагора. Она даже занесена в книгу рекордов Гиннеса! Простейшее доказательство теоремы есть у древнегреческого математика Евклида. Ученые считают, что это доказательство теоремы Евклид придумал сам. В древности, теорему Пифагора знали лишь отдельные ученые, посвященные в таинства математики, теперь ее учат все.

Способы доказательств:

* простейшее доказательство,

* доказательство Евклида,

* Доказательство Эпштейна

* доказательство Перигаля,

* доказательство Нильсена,

* доказательство Бетхера,

* доказательство методом дополнения,

* доказательство методом вычитания,

* алгебраическое доказательство,

* доказательство через косинус угла,

* векторное доказательство,

* геометрическое доказательство методом Гарфилда,

* доказательство индийским математиком Бхаскари-Ачарна,

* «укладка паркета»,

* «стул невесты», и т.д.

Пифагором сначала был доказан лишь частный случай теоремы: им рассматривался равнобедренный прямоугольный треугольник. Чертеж, который используют для доказательства этого случая, в шутку называют «пифагоровы штаны» и добавляют: во все стороны равны.

Знакомясь с разными способами доказательства теоремы Пифагора, мы заметили, что одни из них основаны на свойстве равносоставленных фигур, другие – на дополнении до равных фигур, а третьи - на свойстве равновеликих фигур (имеющие равные площади).

В этой работе мы рассмотрели лишь несколько способов доказательства знаменитой теоремы, однако их существует гораздо больше.

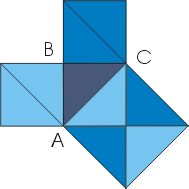
• Простейшее доказательство теоремы получается в простейшем случае равнобедренного прямоугольного треугольника. Вероятно, с него и начиналась теорема. В самом деле, достаточно посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы. Например, для такого треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по 2. Теорема доказана.

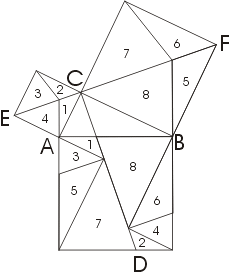• Доказательства методом разложения. Доказательство Эпштейна Начнем с доказательства Эпштейна; его преимуществом является то, что здесь в качестве составных частей разложения фигурируют исключительно треугольники. Чтобы разобраться в чертеже, заметим, что прямая CD проведена перпендикулярно прямой EF.

- Проведем прямую EF, на которой лежат диагонали двух квадратов, построенных на катетах треугольника и проведем прямую CD перпендикулярно EF через вершину прямого угла треугольника.

- Из точек А и В Продлим стороны квадрата, построенного на гипотенузе треугольника, до пересечения с EF.

- Соединим полученные на прямой EF точки с противолежащими вершинами квадрата и получим попарно равные треугольники.

- Заметим, прямая CD делит больший квадрат на две равные прямоугольные трапеции, которые можно разбить на треугольники, составляющие квадраты на катетах. И получим квадрат со стороной, равной гипотенузе треугольника. Теорема доказана.

•Доказательство Нильсена.

Н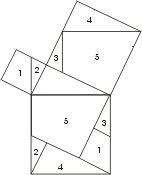 а рисунке вспомогательные линии изменены по предложению Нильсена.

1. Продлим сторону АВ квадрата, построенного на гипотенузе треугольника.

2. Построим прямую EF, параллельную ВС.

3. Построим прямую FH, араллельную АВ.. Построим прямую из точки D, параллельную СН.

5. Построим прямую из точки А, параллельную СG

6. Проведем отрезок MN, параллельный СН

7. Так как все фигуры, полученные в большем треугольнике равны фигурам в квадратах, построенных на катетах, значит площадь квадрата на гипотенузе равна сумме площадей квадратов на катетах.

• Древнеиндийское доказательство «кресло невесты»

В написанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания»), крупнейшего индийского математика XII в. Бхаскары, помещён чертёж с характерным для индийских доказательств словом «Смотри!» Как видим, прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат площадью с² перекладывается в «кресло невесты» с площадью а²+в²

• Еще одно более оригинальное доказательство, предложенное Гофманом.

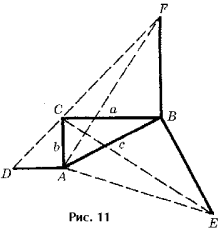Здесь: треугольник ABC с прямым углом C; отрезок BF перпендикулярен CB и равен ему, отрезок BE перпендикулярен AB и равен ему, отрезок AD перпендикулярен AC и равен ему; точки F, C, D принадлежат одной прямой; четырехугольники ADFB и ACBE равновелики, так как ABF=ECB; треугольники ADF и ACE равновелики; отнимем от обоих равновеликих четырехугольников общий для них треугольник ABC, получим

•Доказательство Бетхера.

1. Проведем прямую, на которой лежат диагонали квадратов, построенных на катетах треугольника и опустим из вершин квадратов параллельные отрезки на эту прямую.

2. Переставим большие и маленькие части квадратов, расположенные над осью.

3. Разобьем полученную фигуру как указанно на рисунке и расположим их так, чтобы получился квадрат, сторона которого равна гипотенузе треугольника.

Теорема доказана.

• Доказательство Перигаля.

В учебниках нередко встречается разложение, указанное на рисунке (так называемое "колесо с лопастями"; это доказательство нашел Перигаль). Через центр квадрата, построенного на большем катете, проводим прямые, параллельные и перпендикулярные гипотенузе. Соответствие частей фигуры хорошо видно из чертежа.

• Доказательство методом дополнения.

От двух равных площадей нужно отнять равновеликие части так, чтобы в одном случае остались два квадрата, построенные на катетах, а в другом- квадрат, построенный на гипотенузе.

Н а рис. к обычной пифагоровой фигуре приставлены сверху и снизу треугольники 2 и 3, равные исходному треугольнику 1.

Прямая DG обязательно пройдет через C.

Заметим теперь (далее мы это докажем), что шестиугольники DABGFE и CAJKHB равновелики.

Если мы от первого из них отнимем треугольники 1 и 2, то останутся квадраты, построенные на катетах, а если от второго шестиугольника отнимем равные треугольники 1 и 3, то останется квадрат ,построенный на гипотенузе.

Отсюда вытекает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах.

Остается доказать, что наши шестиугольники равновелики.

Заметим, что прямая DG делит верхний шестиугольник на равновеликие части; то же можно сказать о прямой CK и нижнем шестиугольнике. Повернем четырехугольник DABG, составляющий половину шестиугольника DABGFE, вокруг точки А по часовой стрелке на угол 90; тогда он совпадет с четырехугольником CAJK, составляющим половину шестиугольника CAJKHB.

Поэтому шестиугольники DABGFE и CAJKHB равновелики. Теорема доказана.

• Д оказательство методом вычитания.

Познакомимся с другим доказательством методом вычитания. Знакомый нам чертеж теоремы Пифагора заключим в прямоугольную рамку, направления сторон которой совпадают с направлениями катетов треугольника. Продолжим некоторые из отрезков фигуры так, как указано на рисунке, при этом прямоугольник распадается на несколько треугольников, прямоугольников и квадратов. Выбросим из прямоугольника сначала несколько частей так чтобы остался лишь квадрат, построенный на гипотенузе. Эти части следующие:

1) треугольники 1, 2, 3, 4;

2) прямоугольник 5;

3) прямоугольник 6 и квадрат 8;

4) прямоугольник 7 и квадрат 9;

Затем выбросим из прямоугольника части так, чтобы остались только квадраты, построенные на кататах. Этими частями будут:

1) прямоугольники 6 и 7;

2) прямоугольник 5;

3) прямоугольник 1(заштрихован);

4) прямоугольник 2(заштрихован);

Нам осталось лишь показать, что отнятые части равновелики. Это легко видеть в силу расположения фигур.

Из рисунка ясно, что:

1) прямоугольник 5 равновелик самому себе;

2) четыре треугольника 1,2,3,4 равновелики двум прямоугольникам 6 и 7;

3) прямоугольник 6 и квадрат 8, взятые вместе, равновелики прямоугольнику 1 (заштрихован);;

4) прямоугольник 7 вместе квадратом 9 равновелики прямоугольнику 2(заштрихован);

Теорема доказана

• Приведём наиболее простое геометрическое доказательство этой теоремы:

площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

Н арисуем два квадрата, стороны которых равны (a+b) – сумме двух катетов (сторон, образующих прямой угол) прямоугольного треугольника (рис. 1). Затем в полученных квадратах выполним построения (рис.2, рис.3).

Все зарисованные на рис.2,3 фигуры – квадраты со сторонами, равными катетам и гипотенузе прямоугольного треугольника. Очевидно, что сумма площадей зарисованных квадратов на рис.2 равна площади зарисованного квадрата на рис.3, а именно площади квадрата со стороной (a+b) за вычетом четырех площадей равных между собой треугольников (Слайд 6).

Итак, теорема Пифагора доказана.

Теорема Пифагора (без доказательства) встречается еще в вавилонских текстах, написанных за 1200 лет до Пифагора. Она была известна в Китае и Индии. Одно из древнейших доказательств теоремы Пифагора, очень громоздкое и трудное, дано Евклидом. О прямоугольном треугольнике со сторонами 3,4,5 единиц длины за 200 лет до н.э. знали и египтяне, считая его магическим.

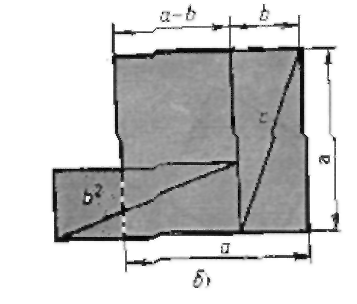
• Древнекитайское доказательство.

Математические трактаты Древнего Китая дошли до нас в редакции II в. до н.э. Дело в том, что в 213 г. до н.э. китайский император Ши Хуанди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги. Во II в. до н.э. в Китае была изобретена бумага и одновременно начинается воссозда­ние древних книг. Так возникла тематика в девяти книгах главное из сохранившихся математико-астрономических сочинений в книге «Математики» помещен чертеж (Рис. а) доказывающий теорему Пифагора.

На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a+b, а внутренний квадрат со стороной с, построенный на гипотенузе. (рис. б). Если квадрат со сторо­ной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (рис. в), то ясно, что образовавшаяся пустота, с одной стороны, равна с, а с другой а²+b² т.е. c²=a²+b²

Н а рисунке воспроизведен чертеж из трактата «Чжоуби...».

Здесь Теорема Пифагора рассмотрена для египетского треугольника с катетами 3, 4 и гипотенузой 5 единиц измерения. Квадрат на гипотенузе содержит 25 клеток, а вписанный в него квадрат на большем катете - 16. Ясно, что оставшаяся часть содержит 9 клеток. Это и будет квадрат на меньшем катете.

• Доказательство Евклида

приведено в предложении 47 первой книги «Начал»

Это доказательство было приведено Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".

Н а гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник JCEL - квадрату АGКС. Тогда сумма площадей квадратов на катетах будет равна площади квадрата на гипотенузе. В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними: FB = AB, BC = BD, а углы между ними равны как тупые углы со взаимно перпендикулярными сторонами. SABD = 0,5S BJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=0,5S ABFH

(BF-общее основание, АВ-общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD=SABFH.

Аналогично, если вы проведёте отрезок АЕ используете равенство треугольников ВСК и АСЕ, то докажете, что SJCEL=SACKG.

Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED, что и требовалось доказать.

• Лично нам больше понравилось алгебраическое доказательство

через косинус острого угла прямоугольного треугольника.

П усть ABC данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С (рис. 8).

По определению косинуса угла (Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе)

На уроках иногда бывают случаи, когда ученики помнят формулировку теоремы, но забывают с чего начать доказательство. Чтобы этого не произошло с нами, мы придумали рисунок – опорный сигнал и, думаем, он надолго останется в нашей памяти.

Отрубил Иван-царевич дракону голову, а у него две новые выросли. На математическом языке это означает: провели в Δ АВС высоту CD, и образовалось два новых прямоугольных треугольника ADC и BDC.

cosA=AD/AC=AC/AB. Отсюда AB*AD=AC². Аналогично cosB=BD/BC=BC/AB. Отсюда AB*BD=BC². Складывая полученные равенства почленно и замечая, что AD+DB=AB, получим: AC²+BC²=AB(AD + DB)=AB².

4. Исторические задачи

Предлагаем несколько исторических задач, найденных в древних источниках.

- Задача Бхаскари

«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Решение: По теореме Пифагора АВ²= ВС²+АС² ;9+16=25, АВ=5 Футов; СD=3+5=8 футов. Ответ: высота тополя 8 футов.

- Задача из китайской «Математики в девяти к нигах»

«Имеется водоем со стороной в 1 чжан = 10 чи. В центре его растет камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды, и какова длина камыша?». Решение: По теореме Пифагора (x+1)²=x²+25; 2x=24, x=12 чи.; 12+1=13 чи.

Ответ: глубина воды-12 чи, длина камыша-13 чи.

- Задача из учебника «Арифметика» Леонтия Магницкого « Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать». Решение: ВС²=АВ²-АС²; ВС²=15625-13689=44 стоп. Ответ: ВС=44 стоп. (Приложение№3).

- Задача о бамбуке из древнекитайского трактата "Гоу-г у"

Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).Какова высота бамбука после сгибания? Решение: (10-x)²=x²-9; -20x=9-100, -20x=-109, x=109/20 чи. Ответ: x= 4,55 чи.

Практические задачи.

1. Над озером тихим с полфута размером,

Высился лотоса цвет. Он рос одиноко. И ветер порывом

Отнёс его в сторону. Нет боле цветка над водой.

Нашёл же рыбак его ранней весною в двух футах от места, где рос.

Итак, предложу я вопрос: «Как озера вода здесь глубока?»

2. Когда мы проводили на дачу свет, нам надо было рассчитать длину электрического провода от домика высотой 2,5м до столба высотой 8,5м.

«Выручила» теорема Пифагора . (Расстояние от столба до домика 8 м)

3. Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)

4. На площади устанавливают елку высотой 12 метров. Для этого нужны растяжки из проволоки исходящие от вершины и находящиеся на расстоянии 5 м от основания ёлки. Хватит ли 50 метров проволоки, чтобы установить елку с помощью 4 растяжек?

5.Теорема Пифагора в строительстве и архитектуре

Очень легко можно воспроизвести способ построения

"натягивателями веревок" прямых углов при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого. Прямой угол окажется заключенным

м ежду сторонами длиной в 3 и 4 метра.

Окно

В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон. На рисунке представлен простой пример такого окна в готическом стиле. Способ построения его очень прост: из рисунка легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг половине ширины, (b/2) для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Т. к. она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, т. е. b/2 и, следовательно, радиус равен b/4. А тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления; покажем, как применяется в таких задачах теорема Пифагора.

В романской архитектуре часто встречается мотив, представленный на рисунке, если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4+p, один катет равен b/4, а другой b/2-p. По теореме Пифагора имеем: (b/4+p)²=( b/4)²+( b/2-p)²; или b²/16+ bp/2+p²=b²/16+b²/4-bp+p²; откуда bp/2=b²/4-bp. Разделив на b и приводя подобные члены, получим: (3/2)p=b/4, p=b/6.

Строительство крыши

При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки. Например: в доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки AC=8 м., и AB=BF.      Решение:     Треугольник ADC - равнобедренный AB=BC=4 м., BF=4 м. Если предположить, что FD=1,5 м., тогда из треугольника DBC: DB=2,5 м., из треугольника АВF:  АF=√4²+4²=√32≈5,7 м.

Взяв за основу эту задачу, мы решили исследовать двускатную крышу детского сада «Цыплёнок» и проверить, выполняется ли для неё теорема Пифагора. Проведя измерения крыши, получили следующие результаты: длина балки -12,2 м., высота – 3 м., длина стропила – 6,8м. Двускатная крыша в сечении – равнобедренный треугольник, тогда длину стропила вычисляем по теореме Пифагора: √6,1²+3² ≈6,8м. Учитывая погрешность измерения, приходим к выводу, что строители крыши при строительстве крыши пользовались известной теоремой.

Мы знаем теперь, что для строительства крыши дома обязательно надо применить теорему Пифагора. При проектировании любых строительных объектов возникает необходимость вычислять стороны прямоугольных треугольников по известным сторонам. Подобные задачи решаются и в нашей повседневной жизни.

Установка ёлки

Н апример, перед новым годом в городе Володарске на небольшой площади перед ДК Юбилейным устанавливается ёлка высотой 5 м. Её всегда устанавливают на прямоугольную призму, сделанную из снега. Ёлка стоит неустойчиво (это проблема) и под воздействием природных явлений (чаще сильного ветра) накреняется и может упасть. Мы предлагаем устанавливать её другим способом. Установить ёлку без снежной призмы высотой 8м. и закрепить её в вертикальном положении. Для этого от вершины ёлки надо сделать проволочные натяжки АВ, АМ, АК одинаковой длины и закрепить на земле на расстоянии 6м от основания елки. Длина натягивающей проволоки должна 10м., т.к. по теореме Пифагора АВ²= АС²+ВС²; АВ= =10 м.

А если все-таки высота ёлки 5м., то длину можно рассчитать приближенно. Пусть натягивающую проволоку закрепим на расстоянии 3 м. от основания ёлки, тогда её длина будет равна = ≈5,8 м.

Молниеотвод

Молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты.

Определим оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту. Решение: по теореме Пифагора h2 ≥ a2+b2, значит h ≥ √(a2+b2). Ответ: h ≥√ (a2+b2).

Гроза и ее непременный атрибут молния – атмосферное явление, таящее в себе достаточно большую опасность. Достаточно сказать, что в год в мире от удара молнии гибнет более 3000 человек (что гораздо больше числа погибших в авиакатастрофах), а материальный ущерб исчисляется миллиардами долларов (в нашей стране - сотнями миллионов рублей).

Мы считаем, что возведение молниеотводов очень актуально для нашего села, т.к. природные катаклизмы не обходят стороной и нас. Так в 2009 году в Новосибирской области в здание детского сада, во время сильной грозы, «зашла» молния. Она «зашла» и «вышла» через крышу, повредив электроснабжение. Весь шифер с одной стороны был полностью снесён. К счастью никто не пострадал. На крыше садика молниеотвода не было. Мы считаем, что он обязательно должен быть на здании, где находятся дети. Поэтому предлагаем на крыше детского садика восстанавливать стержневой молниеотвод.

Если размеры крыши садика 44м. и 12,2м., то по предыдущей задаче высота молниеотвода должна быть h≥√6,12+222, h≥22,8м.

Так как молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты, то высота молниеотвода должна быть не меньше 11,4 м. По расчетам видно, что высота молниеотвода очень высокая. Можно установить два стержневых молниеотвода, мы думаем, это будет экономически выгоднее. Их высоты должны быть не менее 6,3 м., а если учесть ещё и высоту крыши 3 м., то высоты молниеотводов должны быть не менее 3,3 м.

В мобильной связи

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, радиусе R=200 км, если известно, что радиус Земли равен 6380 км.?) Мы на основе задачи, найденной в Интернете, решили решить задачу: какую наименьшую высоту должна иметь вышка мобильной связи, поставленной в селе Мячково, чтобы посёлок Ильино попал в зону связи (расстояние от вышки до Ильино по прямой 10 км.)? Решение: Применив теорему Пифагора, получили уравнение

(х+6380)²=10²+6380²; х²+12760х-100=0;

D=162817600+400=162818000;

≈12760,016;

х≈0,008км.

Вышка мобильной связи

Задача: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, радиусе R=200 км, если известно, что радиус Земли равен 6380 км.?)

Решение:

Пусть AB= x, BC=R=200 км, OC= r =6380 км.
OB = OA + AB
OB = r + x
Используя теорему Пифагора, получим (6380+х)²=6380²+200²

6380²+12760х+х²-6380²-40000=0; х²+12760х-40000=0

D=162817600+160000=162977600; √162977600≈12766; х≈(-12760+12766)/2≈3км.
Ответ: 3км.

в литературе

Мало кто знает, что Пифагор имел отношение не только к математике, но и к литературе. Он и его теорема воспеты в литературе. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, греческий ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.

Существуют много легенд, мифов, рассказов, песен, притчей, небылиц, анекдотов, частушек об этой теореме. Некоторые из них мы приведём в своей исследовательской работе Легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков, послужила поводом для юмора в рассказах писателей и в стихах поэтов.

Так, например, немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в кругосветном путешествии на русском корабле "Рюрик", написал следующие стихи:

Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье.

За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать.

От страха, что вселил в них Пифагор.

Популярность теоремы столь велика, что её доказательства встречаются даже в художественной литературе, например в рассказе известного английского писателя Хаксли "Юный Архимед". Такое же доказательство, но для частного случая равнобедренного прямоугольного треугольника приводится в диалоге Платона "Менон". Этой теореме даже посвящены стихи.

О теореме Пифагора

Суть истины вся в том, что нам она - навечно.

Когда хоть раз в прозрении ее увидим свет,

И теорема Пифагора через столько лет

Для нас, как для него, бесспорна, безупречна.

На радостях богам был Пифагором дан обет:

За то, что мудрости коснулся бесконечной.

Он сто быков заклал, благодаря предвечных;

Моленья и хвалы вознес он жертве вслед,

С тех пор быки, когда учуяв, тужась,

Что к новой истине людей опять подводит след,

Ревут остервенело, так что слушать мочи нет,

Такой в них Пифагор вселил навеки ужас.

Быкам, бессильным новой правде противостоять,

Что остается? - Лишь глаза закрыв, реветь, дрожать.

Легенда о смерти Пифагора

Сонную тишину ночного Метапонта прорезал ужасный крик.

Послышалось падение на землю тяжелого тела, топот убегающих ног, и все смолкло. Когда ночной караул прибыл на место происшествия, в колеблющемся свете факелов все увидели распростертого на земле старца, и неподалеку от него - мальчик 12 с лицом, перекошенным от ужаса.
- Кто это? - спросил начальник караула у мальчика
- Это Пифагор, - ответил тот.
- Кто такой Пифагор? Среди жителей города нет гражданина с таким именем.
- Мы недавно прибыли из Кротона. Мой господин должен был скрываться от врагов, и выходил только ночью. Они выследили его и убили.
- Сколько их было?
- Я этого не успел заметить в темноте. Они отбросили меня в сторону и накинулись на него. Начальник караула стал на колени и приложил руки к груди старца.
- Конец, - сказал начальник.

Т еоремой Пифагора и пифагорейской школой восхищается человечество на протяжении всей истории, им посвящают стихи, песни, рисунки, картины.

Так художник Ф.А. Бронников (1827-1902) нарисовал картину «Гимн пифагорейцев восходящему солнцу»

Картина передает пафос преклонения учеников легендарной школы перед единой гармонией, царящей в мироздании («космосе»), музыке и числе.

III Заключение

В первой главе исследовательской работы мы рассмотрели биографию Пифагора и историю возникновения теоремы Пифагора.

О том, что теорема «квадрат гипотенузы равен сумме квадратов катетов» восходит к Пифагору, утверждали древнегреческий писатель и историк Плутарх (Iв.) и древнегреческий философ – идеалист Прокл (Vв.).

Долгое время считали, что до Пифагора эта теорема не была известна, и поэтому ее назвали «теоремой Пифагора». С таким названием она и сейчас изучается в курсе планиметрии средней школы.

Однако, известно, что она применялась для решения различных задач задолго до Пифагора древними египтянами, вавилонянами, китайцами, индусами и другими древними народами.

Во второй главе мы рассмотрели различные способы доказательства теоремы Пифагора. Пифагором сначала был доказан лишь частный случай теоремы: им рассматривался равнобедренный прямоугольный треугольник. Чертеж, который используют для доказательства этого случая, в шутку называют «пифагоровы штаны» и добавляют: во все стороны равны.

Знакомясь с разными способами доказательства теоремы Пифагора, мы заметили, что одни из них основаны на свойстве равносоставленных фигур, другие – на дополнении до равных фигур, а третьи - на свойстве равновеликих фигур (имеющие равные площади). В этой работе мы рассмотрели лишь несколько способов доказательства знаменитой теоремы, однако их существует гораздо больше.

В третьей главе мы рассмотрели различные интерпретации теоремы Пифагора.

Мы рассмотрели несколько элементарных примеров практических задач, в которых при решении применяется теорема Пифагора.

В результате проведённого исследования мы выяснили некоторые области применения теоремы Пифагора. Нами собрано и обработано много материала из литературных источников и интерната по данной теме. Мы изучили некоторые исторические сведения о Пифагоре и его теореме, решили ряд исторических задач на применение теоремы Пифагора.

Значение теоремы Пифагора состоит в том, что с ее помощью можно вывести большинство теорем геометрии и решить множество задач. Благодаря такому количеству доказательств, теорема Пифагора попала в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. Теорема Пифагора послужила источником для множества обобщений и плодородных идей.

Трудно найти человека, у которого имя Пифагора не ассоциировалось бы с его теоремой.

Даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о "пифагоровых штанах".

Главным в работе считаем предложения по решению выдвинутых нами двух проблем: возведение молниеотвода на крыше детского сада и установке новогодней ёлки. В результате решения поставленных задач мы пришли к выводу, что выдвинутая гипотеза нашла подтверждение. Да, действительно, с помощью теоремы Пифагора можно решать не только математические задачи. Теорема Пифагора нашла своё применение в строительстве и архитектуре, мобильной связи, литературе. А также практическое применение теорема найдёт и при решении тех проблем, которые мы обозначили в своей работе и думаем, что администрация нашего города откликнется на наши предложения.

Результатом нашей работы является:

1. приобретение навыка работы с литературными источниками;

2. приобретение навыка поиска нужного материала в Интернете;

3. научились работать с большим объёмом информации, отбирать нужную информацию;

4. это наш второй проект по математике, в результате которого мы приобрели опыт обработки данных и написания исследовательского проекта.

Было интересно почувствовать себя исследователем, но главное нас заинтересовал процесс познания. Работа над проектом помогла нам реально применить полученные на уроках знания, навыки, опыт в практической деятельности, в соответствии с нашими интересами.

IV.Литература:

1. Атанасян Л.С. и др. «Геометрия 7-9», М. «Просвещение»,2002, с.383

2. Волошинов А.В. «Математика и искусство», М. «Просвещение», 2000, с.117-119, с.399

3. Волошинов А.В. «Пифагор», М. «Просвещение», 1993,с.223

4. Литцман В. «Теорема Пифагора»,М. «Государственное издательство физико-математической литературы», 1960, с.114

5. Погорелов А.В.«Геометрия 7-11», М.«Просвещение»1992, с.383

6. Руденко В.Н. «Геометрия 7-9», М. «Просвещение»1992,с.383

7. http://encyklopedia.narod.ru/bios/nauka/pifagor/pifagor.html

8. http://moypifagor.narod.ru/use.htm

9. http://moypifagor.narod.ru/literature.htm

10. http://th-pif.narod.ru/dopoln.htm

11. http://ega-math.narod.ru/Books/Pythagor.htm

V Приложение

Приложение №1

Заповеди, откровения

- Мысль - превыше всего между людьми на земле.

- Не садись на хлебную меру (т. е. не живи праздно).

- Уходя, не оглядывайся (т. е. перед смертью не цепляйся за жизнь).

- По торной дороге не ходи (т. е. следуй не мнениям толпы, а мнениям немногих понимающих).

- Ласточек в доме не держи (т. е. не принимай гостей болтливых и не сдержанных на язык).

- Будь с тем, кто ношу взваливает, не будь с тем, кто ношу сваливает (т. е. поощряй людей не к праздности, а к добродетели, к труду).

- В перстне изображений не носи (т. е. не выставляй напоказ перед людьми, как ты судишь и думаешь о богах).

Приложение №2

• Великие тайны Пифагора

Первая тайна заключается в таком множестве названий: «теорема бабочки», «т. невесты», «т. нимфы», « т. 100 быков», «бегство убогих», «мост ослов», «ветряная мельница». Думаю, что не найти другой теоремы, которая имела бы столько всевозможных названий!

Вторая тайна – точно неустановленное количество доказательств знаменитой теоремы Пифагора Самосского. Именно по этому поводу я решила провести социологический опрос, который показал, что большинство людей старшего поколения согласны с существованием 250 доказательств, хотя мне из дополнительных источников известно, что существует более 350 доказательств этой теоремы, поэтому она даже попала в Книгу рекордов Гиннеса! Но, конечно же, принципиально различных идей в этих доказательствах используется сравнительно немного.

Третья тайна – это то, что теорема Пифагора является сегодня символом математики.

Четвёртая тайна – теорема Пифагора представляет нам богатейший материал для обобщения – важнейшего вида мыслительной деятельности, основы теоретического мышления, которым в совершенстве владеют многие учёные. Здесь можно добавить, что от теоремы Пифагора можно перейти к другим теоремам.

Пятая тайна заключается в том, что некоторые исследователи приписывают Пифагору доказательство, которое Евклид приводил в первой книге своих «Начал». С другой стороны, Прокл (математик V в.) утверждал, что доказательство в «Началах» принадлежало самому Евклиду. Но всё-таки сегодня способ доказательства Пифагора остаётся неизвестнымШестая тайна – легенды о самом Пифагоре, человеке, который первым доказал эту теорему. Существует легенда, что когда Пифагор Самосский доказал свою теорему, он отблагодарил богов, принеся в жертву 100 быков. Также о гипнотических способностях учёного ходили легенды: будто он одним своим взглядом мог менять направление полёта птиц. А ещё рассказывали, что этого удивительного человека одновременно видели в разных городах, между которыми было несколько дней пути. И что ему якобы принадлежало «колесо фортуны», вращая которое, он не только предсказывал будущее, но и вмешивался, если это было необходимо, в ход событий.

16