Исследовательская работа " Музыкальная математика или математичная музыка"

МБОУ СОШ №39 г. Троицк

Исследовательская работа на тему

«Музыкальная математика, или

математичная музыка»

Выполнила: Андреева Елизавета

ученица 2 «а» класса

МБОУ СОШ №39 г. Троицк

Руководитель:

Кисилева Елена Фаритовна

учитель начальных классов МБОУ СОШ №39 г. Троицк

Троицк, 2013

Содержание

І.	Введение		3
ІІ.	Основная часть		4
1.	Теоретическое содержание исследования		4
1.1.	Зачем нужна музыка?		4
1.2.	Влияние музыки на развитие ребенка		4
1.3.	Выдающиеся музыканты и ученые		6
1.4.	Музыкальная математика или математичная музыка		7
2.	Практические исследования		11
2.1.	Диагностика учащихся, интервьюирование		11
ІІІ.	Заключение		13
IV.	Литература		14
	Приложения		15

I. Введение

«Математика и музыка

требуют единого мыслительного процесса»

                                      (Альберт Энштейн)

Один из самых интересных школьных предметов для меня – это математика. Математика окружает нас повсюду: в строительстве, в быту, в химических процессах, в физических явлениях, в информационных инновациях, в изобразительном искусстве. Мы встречаемся с математикой в нашей жизни не только, когда нам приходится проводить какие-то вычисления или рассматривать какие-либо фигуры, но даже когда мы слушаем музыку, мы соприкасаемся с математикой. Дополнительно я учусь во 2-м классе Детской музыкальной школы №3 на фортепианном отделении. С большим увлечением посещаю музыкальную школу, так как это очень важно для меня и интересно. Еще вместе с одноклассниками я занимаюсь в школьной вокальной группе «До, ми, соль-ка».

Однажды я задумалась, а существует ли связь между такими разными предметами, как музыка и математика, в частности как музыка влияет на развитие математических способностей детей? Показалось интересным найти эти связи, найти ответ. Все это меня и подтолкнуло на написание этой исследовательской работы.

Актуальность проблемы исследования обоснована тем, что на сегодняшний день значимость музыкального образования значительно снижается. Люди забывают о том, что музыка и математика – родные сёстры, что они просто созданы помогать друг другу. Родители, задумываясь, почему их ребёнок плохо успевает по математике, не принимают во внимание тот факт, что музыкальное образование значительно повышает способность к математике.

Объект исследования: музыка и математика.

Предмет исследования: влияние музыки на развитие математических способностей учащихся

Цель исследования: 

Проследить связь между музыкой и математикой в школе.

Задачи исследования:

1. Изучить научно-популярную литературу по данной теме.

2. Определить, помогают ли занятия музыкой выполнять математические задания.

3. Сделать выводы о проделанной работе.

Методы исследования:

1. Разбор научной литературы.

2. Интервью. Тестирование.

Гипотеза: Я предполагаю, что музыка помогает развивать математические способности

II. Основная часть

1.Теоретическое содержание исследования

1.1. Зачем нужна музыка?

Музыка - это древнейшее искусство. Она не ограничена ничем, кроме фантазии композитора. С ее помощью люди многие века грустят, радуются, задумываются о чем-то, отдыхают, танцуют. Для чего же человечеству нужен такой загадочный мир как музыка?

Музыка зародилась многие века назад на Африканском континенте. Историки считают, что самыми первыми музыкальными инструментами были примитивные ударные, а вслед за ними появился прототип современной флейты. Но еще задолго до этого древние люди извлекали различные звуки при помощи тростника, рогов убитых животных, камней, костей и прочих материалов. По мере эволюционного развития общества прогрессировала и музыка. Появлялись новые инструменты, музыкальные жанры, направления и стили. Была разработана нотная азбука. Все это произошло за счет огромной любви человека к ритму и мелодии.

Музыка в нашей жизни занимает важное место, и множество людей даже не мыслят жизни без нее. Она способна подбодрить нас в трудную минуту и напомнить о счастливых моментах жизни. Она играет важную роль в памятных фрагментах жизни каждого человека. Слушая музыку, некоторые люди в словах песен находят свою личную историю из жизни, из-за чего появляются чувства и мысли, которые мы переживаем во время прослушивания композиции.

1.2. Влияние музыки на развитие ребенка

В настоящее время немногие родители  спешат привести своих детей в Детские школы искусств на музыкальное отделение, обучать игре на музыкальных инструментах. Сейчас в моде целенаправленное образование: экономист, юрист, математик, переводчик  и так далее. И так считают многие, зачем тратить время на музыкальные занятия, изнурительные как для родителей, так и для детей, но предыдущие  поколения родителей старались обязательно дать своим детям музыкальное воспитание, продолжая традиции положенные в основу воспитания в дворянских семьях. Как мы знаем из истории в каждой дворянской семье детей обучали иностранным языкам, танцам, игре на музыкальных инструментах, пению, фехтованию, верховой езде. Конечно, занятия музыкой требуют упорного, неустанного труда, волевых усилий, ведь совершенство в исполнении рождается лишь в процессе большой и длительной работы. Профессионалами становятся единицы, но учить нужно всё-таки всех или почти всех, это необходимо. Почему? Остановимся на нескольких аспектах, которые заслуживают особого внимания.

Мозг музыканта быстрее обрабатывает информацию. Это объясняется тем, что на музыкальных инструментах играют двумя руками. Музыканты полнее используют творческий потенциал, отпущенный им природой.

Музыкальные занятия воспитывают волю и дисциплину: заниматься на инструменте надо постоянно, регулярно и без перерывов. Занимаясь музыкой, ребенок развивает математические способности, пространственно мыслит, попадая на нужные клавиши, манипулирует звуками, запоминая нотный текст, и знает, что в музыкальной пьесе как в математическом доказательстве: ни убавить, ни прибавить. Профессора-физики и профессора-математики Оксфорда составляют 70% членов университетского музыкального клуба. Музицировать приятнее, чем решать трудные задачи из-под репетиторской палки! Музыка структурна и иерархична: крупные сочинения распадаются на менее крупные части, которые в свою очередь делятся на небольшие темы и фрагменты, состоящие из мелких фраз и мотивов. Стихийное понимание музыкальной иерархии облегчает понимание компьютера, тоже сплошь иерархичного и структурного. Музыка ведет прямо к вершинам компьютерных наук; не случайно фирма Microsoft предпочитает сотрудников с музыкальным образованием. Игра на музыкальных инструментах помогает в усвоении правописания. Способность писать без ошибок зависит не только от знаний правил, овладению грамотным письмом иногда могут мешать нарушения пространственного восприятия. По статистике, 60 % школьников имеют довольно расплывчатые представления о таких понятиях, как право, лево, внизу, вверху и прочее.  Если у ребёнка есть такие проблемы, значит,  он пишет зеркально, например «э» вместо «е»,  «б» вместо «д», переставляет местами буквы и слоги, слова в предложении, а новое предложение пишет с маленькой буквы. Ребёнок, знающий азы игры  на музыкальном инструменте,  этих  затруднений не испытывает: он твёрдо усвоил, где правая, где левая рука. Знание подкреплено наглядностью – перед ним стоят ноты, где ясно обозначены партии левой и правой руки (верхняя строчка – правая рука, нижняя строчка – левая рука), а значит в ребёнке закреплено и такое понятие, как «вверху - внизу». Также игра на музыкальном инструменте сформирует в ребёнке чувство ритма и наладит координацию между слухом и моторикой рук, что позволит хорошо и быстро двигаться пальчикам  при письме, быстро переключаться с одного  движения на другое, делить  при переносе слова на слоги.

В музыкальной школе нельзя перенести на завтра или на неделю вперед зачет по гаммам и классный концерт. Положение артиста на сцене приучает к максимальной готовности «по заказу» и ребенок с таким опытом не завалит серьезный экзамен, интервью при приеме на работу и ответственный доклад. Музыкальные занятия в детстве — это максимальная выдержка и артистизм на всю жизнь. Музыка помогает ориентироваться в нескольких временных процессах: так читающий с листа пианист сразу делает несколько дел — помнит о прошлом, смотрит в будущее и контролирует настоящее. Музыка течет в своем темпе, и читающий с листа не может прерваться, отдохнуть и перевести дух. Так же и авиадиспетчер, оператор ЭВМ или биржевой брокер следит за несколькими экранами и одновременно слушает и передает информацию по нескольким телефонам. Музыка приучает мыслить и жить в нескольких направлениях.

Ребенку-музыканту будет легче бежать по нескольким жизненным дорожкам и везде приходить первым.

1.3. Выдающиеся музыканты и ученые

Изучая особенности личности мастеров искусства, - будь то музыкант, актер, артист балета или художник, - нельзя не заметить, что они все необъяснимым образом группируются вокруг пяти «Т». Это - Талант, Творчество, Трудолюбие, Терпение, Требовательность.

Многие выдающиеся музыканты блистали математической одаренностью: швейцарский дирижер Эрнест Ансерме – профессиональный математик и лучший исполнитель Стравинского; Леонид Сабанеев – выпускник математического факультета Московского университета, прекрасный пианист, композитор и друг Скрябина. Композитор Эдисон Денисов преподавал математику в Томском университете. Выдающийся виолончелист, дирижёр, композитор, педагог, глава русской виолончельной школы второй половины 19 века Карл Давыдов закончил физико-математический факультет, и как вспоминают современники, имел «блистательные способности к чистой и прикладной математике: в квартире его долго сохранялась модель железнодорожного моста, им изобретенного и по словам специалистов вполне достойного внимания».

Огромно число выдающихся и просто успешных людей, которые не стали музыкантами, но, тем не менее, любят музыку и музицируют. Среди них короли и президенты, видные политики и бизнесмены, известные художники и артисты.

В грандиозном исследовании 25 000 американских школьников, было особо отмечено, что дети, учившиеся музыке, с большей вероятностью показывали в математических тестах высшие баллы чем дети, музыке не учившиеся. Выдающийся исследователь таланта и одаренности Стэнли Стейнберг из Йельского университета опубликовал аналогичные результаты: ученики восьмого класса, которые занимались игрой на музыкальных инструментах, показали себя гораздо лучшими математиками чем остальные ученики. Особенно отличились пианисты, которые выиграли по тестовым баллам конкурс по математике.

Наблюдения, взятые из опыта, наука полностью подтверждает: музыкальные и математические операции родственны и содержательно и психологически. Занимаясь музыкой, человек развивает и тренирует свои математические способности, значение которых в наш прагматический век оспаривать невозможно.

Музыка облагораживает эмоционально; музыка обогащает умственно; музыка способствует росту основных человеческих способностей — способности к логическому мышлению и способности к овладению языком и речью. Музыка настолько многогранна и требовательна ко всем человеческим качествам, что не может быть музыканта, который бы не преуспел в любой сфере деятельности. Широкое внедрение музыкального образования — в детском саду, в школе, в вузе и на любом уровне — позволит каждому человеку максимально раскрыть и умножить все свои способности.

1.4. Музыкальная математика или математичная музыка

Теперь давайте посмотрим, как мы, с вами развиваем математические способности на занятиях музыки.

Пение песен про числа, математику и т.д.: Песенка про цифры Автор. Олеся Емельянова (в сокращении) Цифры все легко и просто
Детям выстроить по росту:
Раз, два, три, четыре, пять,
Шесть, семь, восемь, девять, десять!
А теперь давайте вместе
Будем всё вокруг считать

Сколько чашек, ложек, кружек,
Сколько стульев и игрушек,
Сколько мишек, птичек, зайчиков,
Сколько девочек и мальчиков.

Цифры нам запомнить нужно,
Подпевайте хором дружно:
Раз, два, три, четыре, пять,
Шесть, семь, восемь, девять, десять!
Эту маленькую песню
Все должны на свете знать!

Вслушайтесь в эту веселую песенку. С помощью этой песенки можно легко запомнить начальные цифры натурального ряда.

На первых же уроках сольфеджио – так называются уроки музыкальной грамоты – ученики музыкальных школ сразу же сталкиваются с математикой.

Начало счета в музыке: В музыке все надо считать. Как и в математике.

7 нот: до, ре, ми, фа, соль, ля, си;

5 линеек нотного стана;

интервалы (расстояние между звуками):

ч1-чистая прима

м2-малая секунда

б2-большая секунда

м3- малая терция

б3-большая терция и далее.

Длительности нот: Чтобы записать слова – мы используем буквы, числа – цифры, а музыку – ноты. А ноты-то все разные. Одни коротенькие совсем, другие длинные. Эта схема поможет нам запомнить длительность каждой ноты. Каждый ряд этой «нотной пирамиды» равен четырем долям.

о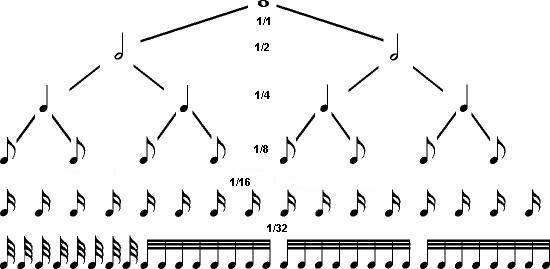 дна целая =4 доли (четверти)

о дна половинка =2 доли (четверти)

о дна четверть =1 доля

о дна восьмая = полдоли

Представьте, что торт надо разрезать на восемь частей. Точно так же целая нота делиться на восемь восьмых.

Доли и дроби: Так в 7 лет ребята, которые занимаются музыкой, узнают, что ноты или что-нибудь другое может делиться. А ведь деление школьники начинают изучать только в 8-9 лет, в конце второго класса.

При записи мелодии, звуки имеют свою длину (длительность).

Здесь и происходит сопоставление целого числа и целой длительности, дробного числа и длительности коротких нот, записываемых при помощи дроби.

Предлагаю рассмотреть нотную запись «Менуэта» Иоганна Себастьяна Баха, исполняемого на фортепиано.

В этой нотной записи:

Целые ноты не используются.

Половинки используются 3 раза. Например, нота ля.

Четверти используются 4 раза. Например, нота ре.

 Восьмые тоже не используются.

Сравнение: Не зная математических понятий, не умея различать дроби, не умея сравнивать их, невозможно было бы сыграть музыкальный фрагмент.

Именно здесь мы сталкиваемся с математической операцией сравнения.

Параллельность: Параллели во множестве встречаются в природе. За всеми параллелями кроются определенные математические закономерности. Траектории капель дождя параллельны, потому что на все капли действуют одинаковые по величине и направлению силы. Гребни морских волн относительно сил ветра тоже параллельны. Но стоит обратиться к творениям рук человеческих, как мы почти в каждом из них обнаружим параллельные элементы. Трамвайные рельсы «параллельны», потому что расстояние между ними всюду одинаково (иначе трамвай не мог бы по ним ехать). Строки на страницах книги расположены параллельно потому, что так удобнее всего для чтения. Полы и потолки в зданиях горизонтальны и, следовательно, параллельны. В музыке, как и в математике, тоже есть понятие параллельности. Параллельные тональности (высоты лада), а ещё линии нотного стана всегда параллельны, то есть, никогда не пересекаются. Параллельные линии можно наблюдать не только в нотах, но и во внешней форме некоторых музыкальных инструментов: вспомним хотя бы о струнах арф или об органных трубах.

Математические последовательности: С понятием последовательность в математике мы встречаемся крайне часто. Обычно цель при встрече с ними – отгадать следующее число или символ.

Из нашего учебника по математике для 2 класса:

Числа от 1 до 100. Задание №1

Запиши числа в порядке их увеличения:

19, 15, 8, 3, 17, 1, 20, 6, 12

Миллиметр. Задание №4

Рассмотри, как получается каждое следующее число в ряду, продолжи его и прочитай числа:

1. 100, 90, 80, 70, 60, □, □, □, □, □.

2. 12, 23, 34, 45, □, □, □, □, □.

3. 98, 88,78, 68, □, □, □, □, □.

Все музыкальные произведения тоже записываются нотами в определенной музыкальной последовательности. Звукоряд представляет собой последовательность ступеней, каждая из которых имеет свою высоту. В мире используются разные системы звукорядов. На западе обычно он состоит из семи нот, в Китае и Африке –из пяти.

2. Практические исследования

2.1. Диагностика учащихся, интервьюирование

В ходе работы был проведён экспериментальный опрос учащихся 2а класса МБОУ СОШ №39. Им было предложено ответить на вопросы: Занимаетесь ли Вы в музыкальной школе, в школьной вокальной группе «До, ми, соль-ка»? Какая у Вас отметка по математике? Также я выяснила, какую часть от общего числа отличников и хорошистов по математике из моего класса составляют ребята, занимающиеся музыкой.

Результаты анкетирования показали:

Из 31 опрошенных учащихся моего класса только 5 человек (16%) играют, на каких либо музыкальных инструментах, 11 человек (35%) одноклассников участвуют в школьной вокальной группе «До, ми, соль- ка» (Приложение №1).

80 % опрошенных учащихся (4 человека), которые посещают музыкальную школу, имеют оценку по математике- 4 и 5 (Приложение №2).

Все 11 человек, участвующих в школьной вокальной группе «До, ми, соль-ка», имеют оценку по математике- 4 и 5.

Больше половины всех отличников и хорошистов по математике из моего класса составляют учащиеся занимающиеся музыкой, 12 учеников из 20. (Приложение №3).

Если сравнивать общие средние показатели, то мы видим, что занятия музыкой положительно сказываются на успеваемости по математике за первую четверть 2013-2014 учебного года.

Нами были протестированы 10 учащихся моего класса, 5 человек из которых учатся в музыкальной школе, другие 5 не получают музыкального образования на предмет решения математических задач. Вопросы тестирования составлены по следующей тематике: последовательности, параллели, доли и дроби. (Приложение №4).

После обработки данных тестирования мы получили следующие результаты (Приложение №5). Из 7 заданий теста, большинство ребят которые учатся в музыкальной школе, справились с 5. Особенно удачно решили задачи на доли и дроби. Школьники, которые не получают музыкальное образование в среднем решили 3 задания. Согласно результатов тестирования можно сделать вывод, что ребятам, которые занимаются музыкой легче справляться с математическими заданиями в школе.

III.Заключение

Я считаю, что цель моей работы достигнута, задачи выполнены. Итак, изучив литературу по данной теме, я узнала, что занимаясь музыкой, человек развивает и тренирует свои математические способности, значение которых в наш век оспаривать невозможно. Исследование доказало: ребятам, которые занимаются музыкой легче справляться с математическими заданиями в школе. Гипотеза подтвердилась. Но для более точного результата, необходимо большее количество исследуемых. Если при более глубоком и многочисленном исследовании, наше предположение будет доказано повторно, это даст человеку еще один способ открыть себя, определить род занятий, выбрать профессию, где наиболее полно раскроется потенциал личности.

Математика и музыка – два школьных предмета, две системы мышления, тесно связанны между собой, потому, что математические и музыкальные операции родственны. Музыка полна математики — темп, такт, размер, гаммы, ритмы, частоты звуков описываются математически.

Музыка настолько многогранна и требовательна ко всем человеческим качествам, что не может быть музыканта, который бы не преуспел в любой сфере деятельности.

IV. Литература

1. «Музыка и поэзия» сост. Е.Н. Домрина.- М.: «Музыка», 1986 г.-64 с.

2. «Про трех китов и про многое другое. Книжка о музыке» Д.Б. Кабалевский.-М.: «Детская литература», 1976 г.

3. «Твой друг музыка» Г.Я. Левашева .- М.: «Детская литература», 1967 г.

4. Учебник «Математика», 2 класс, М.И. Моро, М.А.Бантова и др. М.: «Просвещение», 2012 г. -96 с.

5. «Сольфеджио», 2 класс Ю.Фролова, Ростов на Дону, «Феникс», 2000 г.

6. Энциклопедия «Открой мир вокруг себя: Танец, музыка, театр», ООО «Де Агостини», 2010 г.- 59 с.

7. «Язык, музыка, математика», Варга Б., Димень Ю., Лопариц Э., М.: «Мир», 1981 г.-248 с.

Ссылки

http://solveig.ru/fortepiano.html

http://ru.wikipedia.org

http://www.peoples.ru

Приложение 1

Занимаетесь ли Вы в музыкальной школе, школьной вокальной группе «До, ми, соль-ка»?

Приложение 2

Какая у Вас отметка по математике? (У ребят, посещающих музыкальную школу)

Приложение 3

Какую часть от общего числа отличников и хорошистов по математике из моего класса составляют ребята, занимающиеся музыкой?

Приложение 4

Вопросы тестирования по решению математических задач

Последовательности

1. Каждая из приведенных ниже последовательностей построена по определенному правилу. Установите эти правила и продолжите последовательности:

1) 7, 10, 13, 16, 19, ...

2) 96, 48, 24, 12, ...

3)

4) 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

Параллели

Параллели во множестве встречаются в природе. Траектории капель дождя параллельны, потому что на все капли действуют почти одинаковые по величине и направлению силы. Гребни морских волн относительно сил ветра тоже параллельны. Трамвайные рельсы «параллельны», потому что расстояние между ними всюду одинаково (иначе трамвай не мог бы по ним ехать). Приведите другие примеры параллелей в окружающем мире.

Доли и дроби

Названия музыкальных длительностей служат одновременно и названиями чисел. Например длительность соответствует и дробь 1/8 называются одинаково. Перечень совпадений можно продолжить:

соответствует 1, или

соответствует

соответствует

1. Запишите с помощью чисел равенства =

2. Переведите сумму на язык длительностей

Приложение 5

Результаты выполнения учащимися тестовых заданий.

Участники тестирования	Вопросы тестового задания
	1	2	3	4	5	6	7
Ребята, которые учатся в музыкальной школе
1	+	-	-	-	-	+	+
2	-	-	-	-	+	+	-
3	+	+	-	-	+	+	+
4	+	-	-	-	+	+	-
5	+	+	+	+	+	+	+
Итого	+	+	-	-	+	+	+
Ребята, которые не получают музыкального образования
1	+	-	-	-	+	-	-
2	+	-	-	-	+	+	-
3	+	-	-	-	+	-	-
4	+	-	-	-	-	+	-
5	+	-	-	+	-	-	-
Итого	+	-	-	-	+	+	-

Примечание:

« - » задание решено неверно

« + » задание решено правильно

Правильные ответы на вопросы тестирования.

Последовательности

1) Каждый член последовательности на три больше предыдущего.

2) Каждый член последовательности вдвое меньше предыдущего.

3) Последовательность образована обычными арабскими цифрами и их отражениями в зеркале, приставленном к каждой цифре слева.

4) Два первых члена последовательности равны единице, а каждый из остальных –сумме двух предыдущих членов последовательности. Это последовательность имеет «Собственное имя» и называется последовательностью Фибоначчи.

Параллели

Строки на страницах книги.

Полы и потолки в зданиях горизонтальны и, следовательно, параллельны и т.д.

Доли и дроби

1. ( = )

2. =

17