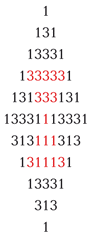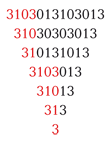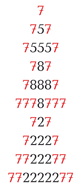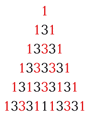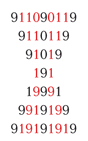МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №4 Г. РОСТОВА
Исследовательская работа по теме:
«Удивительные палиндромы»
Работу выполнил:
Куваев Илья
ученик 8в класса
Руководитель:
Обморышева Ирина Александровна
учитель математики
Ростов, 2020 год
Оглавление.
|
|
| Стр. |
| 1 | Введение. (Актуальность, цели и задачи работы). | 3 |
| 2 | Основная часть. «Удивительные палиндромы». | 4 |
|
| 2.1 | Что такое палиндромы? | 4 |
|
| 2.2 | Из истории появления палиндромов. | 5 |
|
| 2.3 | В каких науках встречаются палиндромы. | 7 |
|
| 2.4 | Числа палиндромы. | 9 |
|
| 2.5 | Практическое применение палиндромов. | 10 |
|
| 2.6 | Интересные факты о палиндромах. | 12 |
| 3. | Заключение | 16 |
| 4. | Список литературы | 17 |
У каждого ученика есть любимые предметы в школе. Мне нравятся уроки математики. На одном из уроков математики, нам сказали придумать палиндромы. Сначала было непонятно, что это такое? Но когда мы стали выполнять это задание, оказалось очень интересно и занимательно. Я люблю узнавать что-то новое. Мне информация стала интересной, и я решил изучить её.
Актуальность работы заключается в возможности получения интересной информации о палиндромах. Тема палиндромов актуальна и интересна с давних времен. Палиндромы обладают необычной историей, удивительными свойствами. В древности к ним относились даже с опаской, считая их заклинаньями. Составлять палиндромы - весьма сложное и кропотливое занятие, но очень интересное. Не каждому под силу и по душе такое занятие.
В настоящее время тема палиндромов также интересна, подтверждением этому являются статьи, различные публикации, сайты в Интернете.
Цель: разобраться в магическом свойстве мира букв и чисел – превращаться наоборот, сохраняя смысл. Научиться составлять числа палиндромы.
Задачи:
Изучить литературу по теме исследования: найти историю возникновения перевёртышей.
Выяснить, что такое палиндром.
Изучить числа-палиндромы.
Рассмотреть палиндромы в других науках.
Составить свои перевёртыши (палиндромы), игры.
Предложить одноклассникам придумать свои перевёртыши (палиндромы),
Объект исследования – палиндромы.
При выполнении работы были использованы следующие
приемы и методы: опрос, анализ (статистическая обработка данных),
работа с источниками информации, исследование.
Теоретическая значимость работы заключается в том, что многие одноклассники и не только, возможно обратят внимание на мое исследование.
Практическая значимость заключается в возможности применения итогов исследования на уроках и во внеурочной деятельности.
Гипотеза: Нас окружают иногда очень интересные слова и числа , но мы редко задумываемся об их происхождении и предназначении. Мир сложно прекрасен и загадочно прост.
Основная часть. «Удивительные палиндромы».
2.1.Что такое палиндромы?
Для того чтобы выяснить, знают ли мои одноклассники про палиндромы я провел опрос.
Задавал такие вопросы:
1.Знаете ли вы, что такое палиндромы?
2. Где встречаются палиндромы?
3. Хотели бы узнать о палиндромах?
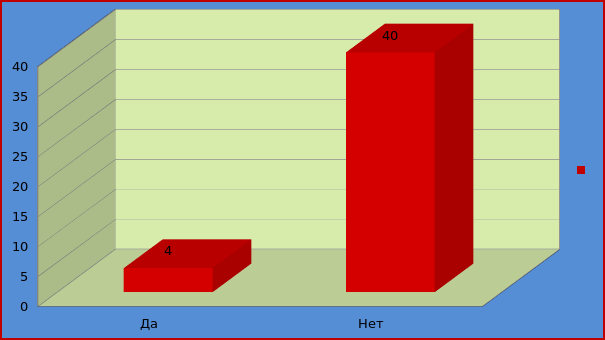
В опросе приняли участие 44 человека. У нас получились следующие результаты. На вопрос знаете ли вы, что такое палиндромы?
Да - ответили 4 человека, нет - 40 человек.
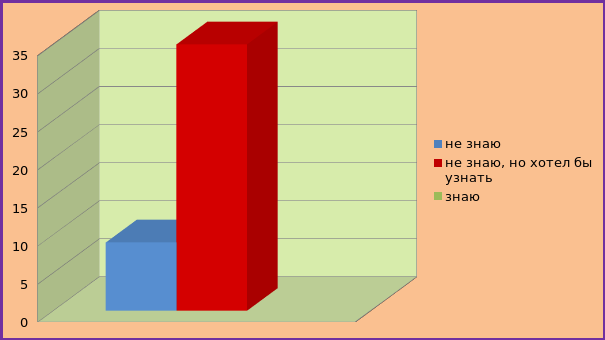
На вопрос: где встречаются палиндромы? Знаю ответили - 0 человек, не знаю -ответили 9 человек, не знаю, но хочу узнать – 34 человека.
Результаты опроса таковы, что одноклассники не знают что такое палиндромы, где они встречаются и пожелали узнать о них.
Я сделал вывод, что необходимо сделать для одноклассников презентацию о палиндромах и на внеурочном занятии познакомить их с ними.
Что такое палиндромы? Я посмотрел в нескольких источниках.
Значение слова палиндром в новом словаре иностранных слов:
Палиндром - (палиндромон) ( гр. palindromeo бегу назад) перевертень - слово, фраза или стих, одинаково читающиеся слева направо и справа налево, напр, кабак , чин зван мечем навзничь (Хлебников).
Значение слова палиндром в Большом энциклопедическом словаре: палиндром то же, что перевертень.
2.2. Из истории появления палиндромов.
Краткая историческая справка
Первые палиндромы появились в Древней Греции, более двух тысяч лет тому назад. Ими украшали амфоры, чаши, вазы и другие предметы округлой формы. Такие палиндромные надписи можно было читать в обе стороны, поворачивая сосуд в руках.
А самый известный из древних палиндромов придумали римляне, которые упаковали его в словесный магический квадрат:
самый известный из древних палиндромов придумали римляне, которые упаковали его в словесный магический квадрат:
Появление этого палиндрома датируется 79 годом нашей эры, а переводится он так: Сеятель Арепо держит колёса в деле.
Этот палиндром одинаково читается не только по горизонтали, но и по вертикали. Необыкновенные свойства квадратного палиндрома так поразили людей того времени, что они считали его магическим и наносили на стены жилищ и монастырей, писали на амулетах. Из-за удивительных свойств этот палиндром считался оберегом от болезней и злых духов.
Много тысячелетий спустя он послужил образцом для самой популярной современной головоломки со словами - кроссворда.
Особенно популярны стали палиндромы в средние века, из коих и дошли до нас такие палиндромные фразы: Otto tenet mappam, madidam mappam tenet Otto. Отто держит карту, мокрый Отто держит карту.
Многими исследователями отмечаются и заговорно-молитвенные свойства палиндромов, которые позволяли использовать их в качестве заклятий. Так, считалось, что при произнесении «оборачиваемой» фразы УВЕДИ У ВОРА КОРОВУ И ДЕВУ должна была восторжествовать справедливость.
Фраза: «На в лоб, болван» использовалась русскими скоморохами как потешка.
Из глубины веков до нас дошли не только латинские, но и греческие палиндромы. В «Поэтическом словаре» А.Квятковского сказано: «В византийском храме Софии в Константинополе на мраморной купели было вырезано следующее палиндромное изречение: «nisponanomimatamimonanopsin», означающее: «Омывайте не только лицо, но и ваши грехи».
Уже к Х-ХI вв. палиндромы распространились сначала в Италии, а затем и в Западной Европе. С ХII-ХIII вв. сведения о них, хотя и редкие, появляются в учебниках поэтики и трактатах по стихосложению. Это связано с открытием первых университетов и формированием единой европейской системы образования, включающей «семь свободных искусств». Риторика, куда входила и поэтика, была важной частью учебного к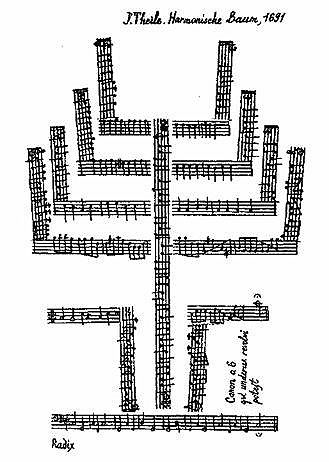 урса.
урса.
К XIV веку относится первое появление в музыке самостоятельной палиндромной формы. Не случайно, что это открытие принадлежит Гийому де Машо (1300-1377) - известному поэту и музыканту, реализовавшему свой замысел в 14-м рондо с символическим для музыкального ряда текстом «Мой конец - моё начало, моё начало - мой конец».
С той поры кто только не интересовался у нас палиндромами – поэты Валерий Брюсов и Андрей Вознесенский (у последнего даже один из сборников стихов и прозы имеет палиндромное название "Аксиома самоиска"), пианист Владимир Софроницкий, актер Владимир Высоцкий, бард Сергей Никитин и многие другие. В частности, среди палиндроманов – так называют себя любители палиндромов – немало ученых. Так или иначе, можно смело сказать, что придумывание симметричных, «двояковыпуклых», как говорил Хлебников, текстов, стало одной из интереснейших словесных забав.
Но наивысшего расцвета палиндром достиг у нас именно в последние годы. Достаточно сказать, что за это время появилось уже свыше сотни газетных и журнальных публикаций на эту тему и даже вышло несколько книг, целиком составленных из палиндромов, проводились фестиваль и конференция по этому вопросу, выходит специальное издание «Амфирифма» клуба палиндроманов.
2.3. В каких науках встречаются палиндромы
Литература
Большой популярностью пользовались палиндромы-фразы, или «афоризмы». Некоторые из них могли даже вызывать улыбку (ввиду своих художественных особенностей). Во многих случаях сочетание внутри перевертыша привлекало внимание не только своей нестандартной формой, но и определенным юмористическим содержанием. Отдельные строки можно даже собирать в стихотворное произведение. Однако если сочетания претендуют на поэзию все-таки, то в них не должно допускаться никаких скидок на необычность форм. Другими словами, все должно сохраняться - ритм, рифма, размеры – как в стандартных, обычных стихотворных произведениях. «Симметричность» в таких случаях добавляла лишь ритмическую и звуковую игру. У многих поэтов получалось находить «почти палиндромные» формы. У разных авторов такие обороты создавали красоту звучания. Говоря о том, что такое палиндром, нельзя не рассмотреть лирические поэтические произведения, созданные с применением данных художественных форм. Многие из них содержат долю юмора, но, несмотря на это, могут быть восприняты достаточно серьезно. Некоторые симметричные выражения хорошо ложатся на музыку. В ряде случаев стихотворное произведение может состоять из одного «перевертыша», разделенного на строки.
Поэзия
Особый интерес на фоне исследования палиндромов представляет творчество Блока. Являясь поэтом-символистом, он достаточно большое внимание уделял ритмической и звуковой организации произведений.
Симметрия в цифрах
Существуют, кроме буквосочетаний, выражений и целых произведений и числа-палиндромы. Данное определение используется при видимой симметрии в записи. Натуральные числа в этом случае будут читаться слева направо и наоборот одинаково. Симметрично может располагаться как нечетное, так и четное количество знаков. Числовые палиндромы встречаются в разных системах, имеющих свои собственные названия. Так, есть категория «фигурных» знаков: 1001, 676 и прочие. Мартин Гарднер, автор книги «Есть идея!», являясь достаточно известным популяризатором науки, выдвигает определенную гипотезу. Если взять натуральное число (любое) и прибавить к нему обращенное (состоящее из тех же цифр, но в обратном порядке), затем повторить действие, но уже с полученной суммой, то на одном из шагов получится палиндром. В некоторых случаях достаточно осуществить сложение единожды: 213 + 312 = 525. Но обычно необходимо не меньше двух операций. Так, например, если взять число 96, то, совершив последовательное сложение, палиндром можно получить только на четвертом уровне: 96 + 69 = 165 165 + 651 = 726 726 + 627 = 1353 1353 + 3531 = 4884
Суть гипотезы состоит в том, что если брать любое число, после определенного количества действий будет обязательно получен палиндром. Примеры можно найти не только в сложении, но и в возведении в степени, извлечении корней и прочих операциях.
Биология
С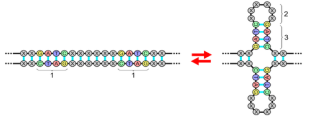 труктура нуклеиновых кислот предусматривает наличие относительно коротких взаимно комплементарных участков. Они имеют так называемые «зеркальные последовательности» из нуклеотидов, способные формировать дуплексы. Палиндромы в биологическом смысле обладают способностью обеспечивать увеличение объема информации без повышения количества нуклеотидов. Особое значение «симметричные формы» имеют при образовании некоторых видов нуклеиновых кислот – транспортных РНК.
труктура нуклеиновых кислот предусматривает наличие относительно коротких взаимно комплементарных участков. Они имеют так называемые «зеркальные последовательности» из нуклеотидов, способные формировать дуплексы. Палиндромы в биологическом смысле обладают способностью обеспечивать увеличение объема информации без повышения количества нуклеотидов. Особое значение «симметричные формы» имеют при образовании некоторых видов нуклеиновых кислот – транспортных РНК.
Музыка
Палиндромные музыкальные произведения играются «как обычно», в соответствии с правилами. После завершения пьесы ноты переворачиваются. Затем произведение играют снова, но мелодия при этом не будет меняться. Интерпретаций может присутствовать сколько угодно, неизвестно при этом, что является низом, а что – верхом. Данные музыкальные произведения можно сыграть вдвоем, при этом читая ноты с обеих сторон одновременно. В качестве примеров таких палиндромических произведений можно привести «Путь мира», написанный Мошелесом, и «Застольную мелодию для двоих», сочиненную Моцартом .
Кроме буквенных, словесных и числовых палиндромов существуют и другие виды не менее интересных палиндромов. В подтверждение этому, я хочу привести некоторые из них в качестве примеров, но уже из других наук
Например, в английском языке: «Madam, I’m Adam» («Мадам, я— Адам,— представился первый человек первой женщине)
В изобразительном искусстве: картинки-перевёртыши.



В химии – НООССООН – формула щавелевой кислоты
Числа палиндромы.
Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо. Иначе говоря, отличаются симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным.
Например: 121; 676; 1331; 4884; 94949; 1177711; 1178711 и т. д.
Изучая палиндромы, я задался вопросом: «Как из других чисел можно получить палиндромы?»
Палиндром можно получить как результат операций над другими числами. Для этого воспользуемся известным алгоритмом.
Алгоритм получения палиндрома
Возьми любое двузначное число
Переверни его (переставь цифры справа налево)
Найди их сумму
Переверни полученное число
Найди их сумму
Повторяй аналогичные действия до тех пор, пока не получится палиндром
Пример:
96
96 + 69 = 165
165 + 561 = 726
726 + 627 = 1353
1353 + 3531 = 4884
В результате проделанной работы я пришел к выводу, что, используя составленный алгоритм, из любого двузначного числа можно получить число-палиндром.
Свойства палиндромов
Теперь обратимся к числам простым. В их бесконечном множестве имеются целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходится на первую тысячу, из них четыре числа однозначные – 2; 3; 5; 7 и всего одно двузначное – 11. С такими числами связано немало интересных закономерностей:
Существует единственный простой палиндром с чётным числом цифр – 11.
Первой и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Все простые двузначные числа, записанные с помощью перечисленных цифр (кроме 19), можно разбить на пары.
Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97.
Среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1.
Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929.
Например: 94849 и 94949; 1177711 и 1178711.
Все однозначные числа являются палиндромами.
26 – наименьшее число, не являющееся палиндромом, квадрат которого палиндром
Например: 26² = 676
А вот пары чисел - «перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр, оказались, связаны хитрым образом:
(1 + 3)2 = 1 + 6 + 9,
(1 + 1 + 3)2 = 1 + 2 + 7 + 6 + 9.
И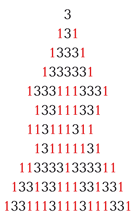 з простых чисел - палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
з простых чисел - палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
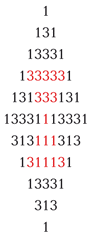
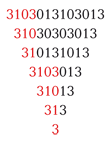
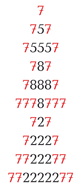
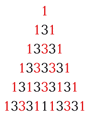
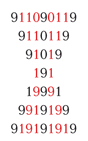
Формулы – палиндромы
Палиндромные формулы вызвали у меня больший интерес. Под формулами – палиндромами понимают выражение, состоящее из суммы или разности, произведения или частного чисел, результат которого не меняется в результате прочтения выражения справа налево.
Например:
42 + 35 = 53 + 24
41 – 32 = 23 – 14
63 ∙ 48 = 84 ∙ 36
2.5. Практическое применение
Исследование №1
Я придумал слова и записал их в алфавитном порядке. У меня получилось 39 слов!
Вот они: Алла, Анна, боб, дед, довод, доход, еле, заказ, иди, или, кабак, казак, как, кок, колок, комок, летел, лил, мадам, мим, наган, око, оно, поп, потоп, пуп, радар, ротор, течет, Тит, топот, тот, тут, ушу, цыц, шабаш, шалаш, шиш.
Среди них 4 глагола (иди, летел, лил, течет), 26 имен существительных
Исследование №2
Существуют целые фразы – палиндромы. Например, одна из таких фраз звучит в известной сказке А. Толстого «Приключения Буратино»:
В сказке девочка Мальвина учила Буратино писать. Она велела написать такую фразу: “А роза упала на лапу Азора” и велела прочитать “наоборот”. Эта фраза одинаково читается слева направо и справа налево. Это фраза-палиндром.
Таких фраз очень много:
Около Мити молоко.
И пиши, и шипи.
На доме чемодан.
Он ест сено.
Лёша на полке клопа нашёл.
Изучая литературу, я натолкнулся на интересный рассказ из готовых палиндромов.
| Ел ёж желе. Лещ овощ ел. Кабак. -Лука ешь не меньше акул! На баке кабан. Нажал кабан на баклажан. - Ешь немытого ты меньше! - Я ем змея! - Я ел млея! Коту тащат уток. И леопард, и гидра поели. - Ещё бы рыб, ещё! Оно, лосося мясо, солоно. А картина манит рака. Арбуз – у зубра. Зубр: ам-ам арбуз! Икру милее не ели Мурки. Тут хорош сырок к еде, крыс шорох тут. - Сырку! – заказ у крыс. А лис – он умён : крыса сыр к нему носила!
| Около Мити молоко. Даст еду деду детсад. - А щи – пища? - Пустите! – Летит супу миска Максиму. – Пустите, летит суп! Что к супу? Скотч? - Ася, молоко около мяса. - Ты, Саша, сыт? - Ем, увы, в уме! - Знамо, даже у ежа дома НЗ. - Лазил Дёма, мёд лизал. - Икни, в студию идут свинки… - Мёд жаждем!!! А клубень – не булка. Пчела звала: - В зале ЧП! - УРА! – вопите, дети, повару. Гори, пламя, – мал пирог. Конец сценок!
|
Исследование №3
Но вернемся к нашим словам – палиндромам. Попробуем закодировать их с помощью цифр. Вместо гласной будем писать цифру – 1, а вместо согласной – 2.
Например: закодируем слово шалаш. Получится -21212
Палиндромические числа давно заинтересовали ученых – математиков. Эти числа не просто красивы, но ещё и обладают рядом замечательных свойств.
1)Например, возьмем число 38. Запишем его в обратном порядке 83. А теперь попробуем их сложить.
38 + 83 = 121 – палиндром.
Мы сделали один шаг и получили палиндром.
2)Иногда, чтобы получить палиндром, требуется больше шагов.
Например: число 67
67+76 = 143
143+341 =484 (палиндром) - два шага
3) А если возьмём число 96 , то палиндром можно получить, сделав четыре шага.
96 + 69 = 165,
165 + 561 = 726,
726 + 627 = 1353,
1353 + 3531 = 4884
Я попробовал найти палиндромы для различных чисел и обнаружил, что:
- в двузначных числах – палиндромах число единиц совпадает с числом десятков (например: 11; 99)
– в трехзначных числах – палиндромах число сотен всегда совпадает с числом единиц (535; 676) .
- в четырехзначных числах – палиндромах (4224; 3113) число единиц тысяч совпадает с числом единиц, а число сотен с числом десятков и т.д.
Интересные факты о палиндромах
1. Теоретики и практики палиндрома выделили многочисленные пограничные с палиндромом формы: например, оборотень — текст, читающийся слева направо иначе, чем справа налево: «Мир удобен» - «Небо дурим»(Сергей Федин).
2. На русском языке наиболее длинным буквенным палиндромом на сегодняшний день является произведение Р. Адрианова «ЦЕН ОКНО», в которой свыше 6 000 букв.
3. Существуют палиндромы не только в русском, но и других языках
русский язык
А в Енисее — синева.
А лама мала.
А лис, он умён — крыса сыр к нему носила. (И. Бабицкий)
Аргентина манит негра.
английский язык
Race fast, safe car (Гони быстро, безопасная машина)
Do geese see God? (Видят ли гуси бога?)
арабский язык: حوت فمه مفتوح (Кит с открытым ртом)
болгарский язык: Кирил е лирик (Кирилл — лирик)
испанский язык: Anita lava la tina (Анита моет корыто)
итальянский язык: Autore, ero tua (Автор, я твоя)
латинский язык: Sum summus mus (Я — сильнейшая мышь)
немецкий язык: Reit nie tot ein Tier (Никогда не гони животное до смерти)
польский язык: Kobyła ma mały bok (У кобылы маленький бок)
португальский язык: Socorram-me, subi no ônibus em Marrocos (Помогите мне, я попал в автобус в Марокко)
татарский язык: Ata qadaq ata (Отец кидает гвоздь)
турецкий язык: Anastas kazak satsana (Анастас, продай свитер)
украинский язык: Кому дикі ріки думок? (Кому дикие реки мыслей?)
чешский язык: Fešná paní volá: Má málo vína pan šéf? (Шикарная пани спрашивает: У пана шефа мало вина?)
финский язык: saippuakauppias (продавец мыла) — самое длинное употребительное слово-палиндром в мире
Просто факты

Российский герб Двуликий Янус

«Палиндромное дело» в Пенькове (Художественный фильм «Дело было в Пенькове»)

Сказочная зверушка Тяни – Толкай

«Свинский» палиндром

Липовый палиндром
Случаются палиндромные имена:
ADA, ANNA, BOB, EVE, HANNAH, OTTO, АННА, АЛЛА, НАТАН, ТИТ
и фамилии:
Нилин, Аникина.
А вот палиндромные имена-фамилии:
Лон Нол (1913–1985) - бывший премьер-министр Камбоджи.
Нисио Исин (Nisio Isin, NisiOisin, настоящее имя Nishio Ishin) – японский писатель и автор манга-книг.
Некоторые литературные деятели умудряются писать палиндромные стихи и рассказы. В этой связи хорошо известны два рассказа на английском языке - Dr Awkward & Olson in Oslo (Доктор Оквард и Олсон в Осло), который Л.Левин (Lawrence Levin) написал в 1986 году, состоит из 31 954 слов, и Veritas (1980), принадлежащий перу Дэвида Стивенса (David Stephens), - 58795 слов. На французском языке написан рассказ Grand Palindrome (1969), в котором 5556 букв.
Зеркальная дата.

Такая дата считается зеркальной из-за уникального повторения цифр (если читать цифры наоборот, получите то же самое число). И эта зеркальность придает ей магию и удачу. Важно еще, что в сумме эта дата дает цифру 8, что означает символ бесконечности и денег, поэтому день 02022020 особенно может помочь в денежных делах.
Примеры других зеркальных дат: 12.02.2021, 22.02.2022, 23.02.2032 и т.д.
3. Заключение.
Мир чисел настолько загадочен и увлекателен, что занимаясь данной работой, я понял, если бы каждый из нас уделял ему больше внимания, то нашел бы для себя много нового и интересного. Я познакомился с удивительными натуральными числами: палиндромами. Данная тема интересна одноклассникам, ее изучение можно продолжить в других предметах: ИЗО, окружающий мир, русский язык и другие.
В мире так много тайн и загадок, которые его украшают, и чудо палиндрома — это тоже одно из неповторимых таинств. Математики связывают с ним множество любопытных фактов и закономерностей: палиндромы делятся на пары и семейства, образуют числовые квадраты и целые симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр. В своей работе я показала, что нас окружают очень интересные вещи, но мы редко задумываемся об их происхождении и предназначении. Пусть эти числа еще не до конца изучены, и не ясно их применение, но может быть в результате таких опытов с числами, и откроется их истинная суть. А пока будем наслаждаться красотой чисел.
Перевёртыши на самом деле очень увлекательны, они помогают развивать интерес к познавательной деятельности. Я узнал, что палиндромы, это не только интересные картинки в изобразительном искусстве и окружающем мире, но и числа в математике, слова и фразы в русском языке. Мой кругозор стал шире, я узнал много интересной и полезной информации.
Я думаю, что моё исследование поможет улучшить память, мышление, воображение.
Думаю, что представленная мной работа будет весьма интересна и полезна ученикам, учителям и всем увлекающимся математикой людям.
Если Вас моя работа заинтересовала, её можно продолжить, найдя новые объекты исследования.
Результаты: Гипотеза подтвердилась.
Изучили литературу по теме исследования: нашли историю возникновения перевёртышей
Рассмотрели свойства палиндромов.
Выбрали предмет и продемонстрировать перевёртыши в математике.
Составили свои перевёртыши (палиндромы), игры.
Предложили одноклассникам придумать свои перевёртыши (палиндромы), решили несколько задач олимпиадного типа по теме.
4. Список литературы
http://www.nkj.ru/archive/articles/17984/ (Наука и жизнь№5,2010г).
Кацюба Е.А.Первый палиндромический словарь.— Москва, 1999.
Е.А.Новый палиндромический словарь.— Москва, 2002.
Федин С.Н. Палиндроматика // Математика для школьников. – 2005. - № 1, с. 54.
Кордемский Б.А. Удивительный мир чисел // книга для учащихся. – М.: Просвещение, 1995.
Кордемский Б. А. На часок к семейке репьюнитов // Квант. -1997. - № 5. - с. 28-29.
Перельман Я.И. Занимательная математика // издательство «Тезис». – 1994
http://arbuz.uz/t_numbers.html
Журнал квант
16









 самый известный из древних палиндромов придумали римляне, которые упаковали его в словесный магический квадрат:
самый известный из древних палиндромов придумали римляне, которые упаковали его в словесный магический квадрат: урса.
урса. труктура нуклеиновых кислот предусматривает наличие относительно коротких взаимно комплементарных участков. Они имеют так называемые «зеркальные последовательности» из нуклеотидов, способные формировать дуплексы. Палиндромы в биологическом смысле обладают способностью обеспечивать увеличение объема информации без повышения количества нуклеотидов. Особое значение «симметричные формы» имеют при образовании некоторых видов нуклеиновых кислот – транспортных РНК.
труктура нуклеиновых кислот предусматривает наличие относительно коротких взаимно комплементарных участков. Они имеют так называемые «зеркальные последовательности» из нуклеотидов, способные формировать дуплексы. Палиндромы в биологическом смысле обладают способностью обеспечивать увеличение объема информации без повышения количества нуклеотидов. Особое значение «симметричные формы» имеют при образовании некоторых видов нуклеиновых кислот – транспортных РНК.


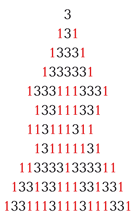 з простых чисел - палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
з простых чисел - палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.