Государственное казенное общеобразовательное учреждение "Общеобразовательная школа-интернат для слепых и слабовидящих обучающихся" г.Троицка
Проект на тему:
«Палиндромы и репьюниты»
Выполнил: Сахаров Артем,
ученик 6А класса
Руководитель: Никитина Л.Ю.,
учитель математики
Троицк 2021 г.
Содержание:
Содержание:
I. Введение..………………………………………………………………..3
Проблема……………………………………………………………..........3
Цель………………………………………………………………………...3
Задачи…………………………………………………………………..…..3
Методы…………………………………………………………………….3
II. Основная часть…………………………………………………..
Теоретическая часть
1.1Числа палиндромы ……………........................................................
1.2 Числа репьюниты………………………………………………………..
Практическая часть ………………………………………………………
2.1 Выводы …………………………………………………………………
2.2 Заключение ………………………………………………………………....
2.3 Приложения ………………………………………………………………
2.4………………………………………………………………………………
2.5………………………………………………………………………………
2.6………………………………………………………………………………
III. Заключение……………………………………………………………….10
IV. Список использованных источников информации………………....12
Введение
Актуальность выбора темы
Числа палиндромы и репьюниты образуют одно из наиболее интересных подмножеств множества натуральных чисел. Они обладают необычной историей, удивительными свойствами.
Мы провели исследование среди 7, 8, 9, 11 классов и выяснили, что многие ребята слышали об этих числах, но подробную информацию знают единицы. Многие из опрошенных учащихся хотели бы узнать об этих числах больше. (Приложение 1)
Проблема
Простые числа – это часть чисел, из которых состоят все натуральные числа.
Исследуя множество простых чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.
Цель исследования
Практически все математические понятия, так или иначе, опираются на понятие числа, а конечный результат любой математической теории, как правило, выражается на языке чисел. Многие из них, особенно натуральные числа по тем или иным признакам и свойствам сгруппированы в отдельные структуры (совокупности) и имеют собственные имена. Таким образом, целью исследования является знакомство с числами палиндромами и репьюнитами.
Задачи исследования
Изучить литературу по теме исследования.
Рассмотреть свойства палиндромов и репьюнитов.
Установить связь между палиндромами и репьюнитами.
Выяснить, какую роль играют простые числа в изменении свойств заинтересовавших нас чисел.
Предмет исследования – множество простых чисел.
Объект исследования – числа палиндромы и репьюниты.
Методы исследования:
теоретический
анкетирование
анализ
2
Теоретическая часть
Числа палиндромы
Вы, наверное, все помните книгу о приключениях Буратино. Помните, как строгая Мальвина учила Буратино писать? Она велела написать такую фразу: “А роза упала на лапу Азора” и велела прочитать “наоборот”. Эта фраза читается слева направо и справа налево. Это фраза-палиндром (в переводе — перевертыш). Слова: ШАЛАШ, РАДАР, ТОПОТ, КОК, КАЗАК — тоже палиндромы.
Числовые палиндромы – это натуральные числа, которые одинаково читаются справа налево и слева направо. Иначе говоря, отличаются симметрией записи (расположения цифр), причём число знаков может быть как чётным, так и нечётным.
Например: 121; 676; 1331; 4884; 94949; 1177711; 1178711 и т. д.
Изучая палиндромы, автор данной работы задаёт вопрос: «Как из других чисел можно получить палиндромы?»
Палиндром можно получить как результат операций над другими числами. Для этого воспользуемся известным алгоритмом.
Алгоритм получения палиндрома
Возьми любое двузначное число
Переверни его (переставь цифры справа налево)
Найди их сумму
Переверни полученное число
Найди их сумму
Повторяй аналогичные действия до тех пор, пока не получится палиндром
Пример:
96
96 + 69 = 165
165 + 561 = 726
726 + 627 = 1353
1353 + 3531 = 4884
В результате проделанной работы автор пришёл к выводу, что, используя составленный алгоритм, из любого двузначного числа можно получить число-палиндром.
Можно рассмотреть не только сложение, но и другие операции над палиндромами. (Приложение 2)
3
Приведем два примера того, как при помощи одних палиндромов получаются другие:
а) 212² - 121² = 44944 – 14641 = 30303;
б) 2·121·10201 = 2·11² ·101² = 22·112211 = 1111· 2222 = 2468642.
Теперь обратимся к числам простым. В их бесконечном множестве имеются целые семейства палиндромов. Только среди первых ста миллионов натуральных чисел насчитывается 781 простой палиндром, причём двадцать приходится на первую тысячу, из них четыре числа однозначные – 2; 3; 5; 7 и всего одно двузначное – 11. С такими числами связано немало интересных закономерностей:
Существует единственный простой палиндром с чётным числом цифр – 11.
Первой и последней цифрами любого простого палиндрома могут быть только 1; 3; 7 или 9. Это следует из известных признаков делимости на 2 и на 5. Все простые двузначные числа, записанные с помощью перечисленных цифр (кроме 19), можно разбить на пары.
Например: 13 и 31; 17 и 71; 37 и 73; 79 и 97.
Среди простых трёхзначных палиндромов встречаются пары чисел, у которых средняя цифра отличается всего на 1.
Например: 181 и 191; 373 и 383; 787 и 797; 919 и 929.
Например: 94849 и 94949; 1177711 и 1178711.
Все однозначные числа являются палиндромами.
26 – наименьшее число, не являющееся палиндромом, квадрат которого палиндром
Например: 26² = 676
А вот пары чисел - «перевёртышей» 13 — 31 и 113 — 311 при возведении в квадрат дают также пары «перевёртышей»: 169 — 961 и 12769 — 96721. Любопытно, что даже суммы их цифр оказались связаны хитрым образом:
(1 + 3)2 = 1 + 6 + 9,
(1 + 1 + 3)2 = 1 + 2 + 7 + 6 + 9.
Из простых чисел - палиндромов, располагая их определённым образом, скажем построчно, можно составить симметричные фигуры, отличающиеся оригинальным рисунком из повторяющихся цифр.
4



Примеры палиндромов
|
В русском языке | Утречко летело к черту Я ем змея Я нем и нежен, не жени меня Я ужру буржуя! Нам рак влетел в карман Цени в себе свинец |
|
Магический квадрат | 
|
|
В биологии |
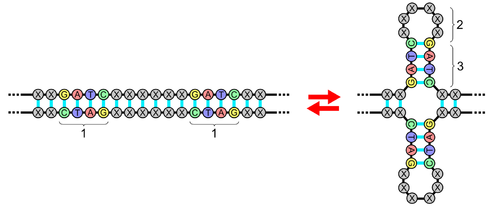
Палиндромы в ДНК 1 - палиндром |
| В химии | НООССООН – формула щавелевой кислоты |
|
В изобразительном искусстве |

|
5
Числа репьюниты
Репьюниты – натуральные числа, запись которых состоит только из единиц.
В десятичной системе счисления репьюниты обозначаются короче Rn: R1 = 1,
R2 = 11, R3 = 111 и т. д., и общий вид для них:
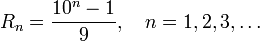
Общий вид репьюнита может быть записан в другом виде:

Например: 11; 111; 1111; 11111; 111111; 1111111 и т. д.
Обнаружено немало интересных свойств репьюнитов:
Репьюниты - частный случай чисел-палиндромов, которые остаются неизменными при прямом и обратном прочтении.
Репьюниты относятся к таким палиндромам, которые делятся на произведение своих цифр.
Известно пять простых репьюнитов: R2, R19, R23, R317 и R1031, причем, что самое интересное - индексы этих репьюнитов также простые числа. Самое маленькое число репьюнит – 1. Самое большое – ещё не найдено.
В семействе репьюнитов выявлено пока только 9 простых чисел: 2, 19, 23, 317, 1031, 49081, 86453, 109297, 270343 (индексы репьюнитов).
Раскладывая некоторые составные репьюниты на простые множители:
111 = 3∙37
1111 = 11∙101
11111 = 41∙ 271
111111 = 3∙7∙11∙13∙37
1111111 = 239∙4649
11111111 = 11∙73∙101∙137
111111111 = 3∙37∙333667 и т. д. можно заметить числа палиндромы.
11∙11 = 121
11∙111 = 1221
1111∙11 = 12221
111∙111 = 12321
11111∙111 = 1233321
11111∙1111 = 12344321
11111∙11111 = 123454321 и т.д.
Перемножив немало репьюнитов, автор данной работы делает вывод о том, что каждый раз получается число палиндром. (Приложение 3)
6
Пример репьюнита
|
В математике 
|
Треугольник, полученный из исходного после добавления к нему шести простых палиндромов. Фигура сразу привлекает внимание своим изящным обрамлением из единиц. Её окаймляют два простых репьюнита одинаковой длины: 23 единицы составляют «основание» и ещё столько же — «боковые стороны» треугольника.
|
В других областях науки примеры репьюнитов не найдены.
7
Практическая часть
Решим две интересные задачи из журнала « Квант» №5 за 1997 год.
Задача №1
К акими цифрами следует заменить буквы, чтобы сумма девяти слагаемых стала равной репьюниту?
акими цифрами следует заменить буквы, чтобы сумма девяти слагаемых стала равной репьюниту?
Решение: 12345679+12345679+12345679+12345679+12345679+12345679+12345679+ +12345679+12345679=111111111 – репьюнит
Ответ: 111111111
Задача №2
Произведением каких двух репьюнитов является число 123455554321?
Решение:
Перемножив два репьюнита, мы получили
11111111 · 11111 = 123455554321.
Ответ: 11111111 · 11111
8
Выводы
Проведя исследование по данной теме, автор изучил свойства палиндромов и репьюнитов, установил связь между ними, выяснил какую роль играют простые числа в изменении свойств данных чисел.
Результаты исследования (сходство и различие) занесены в таблицу.
| Категории сравнения | Палиндромы | Репьюниты |
| Читается слева направо и справа налево одинаково | + | + |
| Симметрия записи (расположения цифр) | + | - Не всегда |
| Число знаков, используемых при записи чисел, может быть чётным и нечётным | + | + |
| Можно получить как результат операций над другими числами: сложение возведение в степень извлечение корня умножение
|
+ + + + |
+ + + + |
| Можно получить многоугольные фигуры | + | + |
| Являются представителями класса простых чисел | + | + |
9
Заключение
Мир чисел настолько загадочен и увлекателен, что занимаясь данной работой, я понял: если бы каждый из нас уделял ему больше внимания, то нашел бы для себя много нового и интересного.
Я познакомился с удивительными натуральными числами: палиндромами и репьюнитами. Все они обязаны своими свойствами простым числам.
Значит, я подтвердил гипотезу о том, что простые числа – это часть чисел, из которых состоят все натуральные числа.
Исследуя множество простых чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.
10
Приложения
Приложение 1
Результаты опроса
«Хотите ли знать больше об этих числах?»
| 
| Палиндромы | Репьюниты |
| Классы | Кол-во учащихся | Хотите узнать больше об этих числах? |
| Да | % | нет | % | да | % | нет | % |
| 7а | 31 | 31 уч. | 100 | 0 уч. | 0 | 31 уч. | 100 | 0 уч. | 0 |
| 8в | 29 | 29 уч. | 100 | 2 уч. | 0 | 29 уч. | 100 | 2 уч. | 0 |
| 9а | 26 | 26 уч. | 100 | 0 уч. | 0 | 26 уч. | 100 | 0 уч. | 0 |
| 11б | 23 | 23 уч. | 100 | 0 уч. | 0 | 23 уч. | 100 | 0 уч. | 0 |
Результаты опроса показали, что все учащиеся хотят знать больше о числах палиндромах и репьюнитах.
Приложение 2
Операции над палиндромами
| Число | Действие | Результат | Полученное число |
| 17 | 17 + 71 | 88 | Палиндром |
| 132 | 132 + 231 | 363 | Палиндром |
| 111 | 111² | 12321 | Палиндром |
| 111111111 | 111111111² | 12345678987654321 | Палиндром |
| 1 | 1·1 | 1 | Палиндром Репьюнит |
| 1 | 
| 1 | Палиндром Репьюнит |
| 121 | 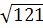
| 11 | Палиндром Репьюнит |
Выполняя действия над палиндромами в результате можно получить и палиндром, и репьюнит.
11
Приложение 3
Произведение репьюнитов дает палиндром.
| 1 множитель | 2 множитель | Произведение |
| 111 | 111 | 12321 |
| 111 | 1111 | 123321 |
| 111 | 11111 | 1233321 |
| 111 | 111111 | 12333321 |
| 1111 | 1111 | 1234321 |
| 1111 | 11111 | 12344321 |
| 1111 | 111111 | 123444321 |
| 11111 | 11111 | 123454321 |
| 11111 | 111111 | 1234554321 |
| 111111 | 111111 | 12345654321 |
| 111111 | 1111111 | 123456654321 |
| 1111111 | 11111111 | 1234567654321 |
| 11111111 | 111111111 | 1234567887654321 |
| 111111111 | 1111111111 | 12345678887654321 |
| 1111111111 | 111 | 123333333321 |
| 11111111111 | 1111 | 12344444444321 |
| 1111111111111 | 111 | 123333333333321 |
| 11111111111111 | 11 | 122222222222221 |
| 111111111111111 | 111 | 12333333333333321 |
Перемножив немало репьюнитов, автор данной работы делает вывод о том, что каждый раз получается число палиндром.
12
Список использованных источников информации
Депман И.Я. За страницами учебника математики //пособие для учащихся 5-6 классов средней школы. – М.: Просвещение, 1989.
Ейтс С. Репьюниты и десятичные периоды // издательство «Мир». – 1992.
Кордемский Б.А. Удивительный мир чисел // книга для учащихся. – М.: Просвещение, 1995.
Кордемский Б. А. На часок к семейке репьюнитов // Квант. -1997. - № 5. - с. 28-29.
Перельман Я.И. Занимательная математика // издательство «Тезис». – 1994
http://arbuz.uz/t_numbers.html
http://www.ipb.su/uploads/ipbsu/maffss/post-11-1375455274.png магический квадрат
http://upload.wikimedia.org/wikipedia/commons/thumb/7/75/DNA_palindrome.svg/640px-DNA_palindrome.svg.png палиндромы в ДНК
http://newcok.ru/_fr/1/4657107.jpg картинки перевёртыши
http://www.nkj.ru/upload/img/2010/5_108/ur9.gif числа палиндромы
http://polit.ru/media/archive/generic/p0001882.jpg числа палиндромы
http://polit.ru/media/archive/generic/p0001887.jpg числа палиндромы
http://polit.ru/media/archive/generic/p0001880.jpg числа палиндромы
Аннотация
Практически все математические понятия, так или иначе, опираются на понятие числа, а конечный результат любой математической теории, как правило, выражается на языке чисел.
Работа посвящена изучению удивительных чисел: палиндромов и репьюнитов, установлению связи между ними. Автор изучает роль простых чисел в изменении свойств палиндромов и репьюнитов.
В работе определена цель исследования, выдвинута и проверена гипотеза: простые числа – это часть чисел, из которых состоят все натуральные числа. Исследуя множество простых чисел, можно получить удивительные числовые множества с их необыкновенными свойствами.














 акими цифрами следует заменить буквы, чтобы сумма девяти слагаемых стала равной репьюниту?
акими цифрами следует заменить буквы, чтобы сумма девяти слагаемых стала равной репьюниту?










