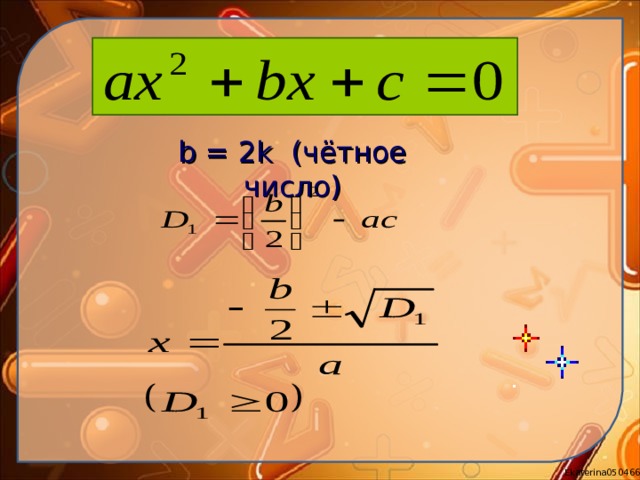О квадратном трёхчлене замолвите слово Феликс Шлейфер

Введение:
- “ Главная” функция в школьном курсе алгебры - это квадратный трехчлен. Он присутствует в разных разделах программы. Поэтому необходимо познакомиться с ним поближе и подружиться.

Гипотеза:
- Перед работой над этим проектом была выдвинута гипотеза, а существует ли связь между коэффициентами квадратного трехчлена с его корнями и знаками этих корней. Давайте проверим верна ли наша гипотеза.

ОБЪЕКТ ИССЛЕДОВАНИЯ:
- Тайны квадратного трехчлена

Предмет исследования:
Исследование квадратного трехчлена .

Цель:
- Дополнить уже известные знания о квадратном трехчлене:
- понятия "квадратного трехчлена";
- умение находить корни квадратного трехчлена;
- формирование навыков самостоятельной работы с большими объёмами информации.

Задачи исследования:
1. Исследование квадратного трехчлена.
2. Как решать квадратные уравнения методом выделения полного квадрата.
3. В чем заключается алгоритм решения квадратного уравнения по формулам.
4.Как решить квадратное уравнение с помощью теоремы Виета.
5. Найти связь между коэффициентами квадратного трехчлена и знаками его корней.

Методы исследования:
- Сбор информации Обработка информации Анализ Обобщение
- Сбор информации Обработка информации Анализ Обобщение
- Сбор информации
- Обработка информации
- Анализ
- Обобщение

Н О В И З Н А
- В ходе выполнения проекта мы расширили свой кругозор о квадратном трехчлене.

Квадратный трехчлен и его корни :
Квадратным трехчленом называется
многочлен вида ax² + bx + c , где x- переменная,
a, b и c - некоторые числа, причем, a≠ 0 .
Корнем квадратного трехчлена называется
значение переменной, при котором значение
этого трехчлена равно нулю .
Чтобы найти корни квадратного
трехчлена ax² + bx + c , необходимо решить
квадратное уравнение ax² + bx + c =0.
 0, b и c – любые, сформулировал Брахмагупта (VII в. н. э.). Брахмагупта еще не знал, что квадратное уравнение может иметь и отрицательный корень. Бхаскара Ачарья (XII в .) сформулировал, соотношения между коэффициентами уравнения. Составил много задач. " width="640"
0, b и c – любые, сформулировал Брахмагупта (VII в. н. э.). Брахмагупта еще не знал, что квадратное уравнение может иметь и отрицательный корень. Бхаскара Ачарья (XII в .) сформулировал, соотношения между коэффициентами уравнения. Составил много задач. " width="640"
Динамическая пауза
- Задачи на нахождение корней квадратного трехчлена и составление квадратных уравнений встречаются уже в древнеегипетских математических папирусах.
- Общее правило нахождения корней и решения уравнений вида: ax ² + bx = c, где a 0, b и c – любые, сформулировал Брахмагупта (VII в. н. э.). Брахмагупта еще не знал, что квадратное уравнение может иметь и отрицательный корень.
- Бхаскара Ачарья (XII в .) сформулировал, соотношения между коэффициентами уравнения. Составил много задач.


Впервые ввёл термин «квадратное уравнение» немецкий философ
- знаменитый немецкий философ, родился в 1679 г. в Бреславле, в семье простого ремесленника, изучал в Йене сначала богословие, потом математику и философию.

В 13 – 16 веках даются отдельные методы решения различных видов квадратных уравнений. Слияние этих методов произвел в 1544 году немецкий математик – Михаэль Штифель.
Это было настоящее событие в математике.
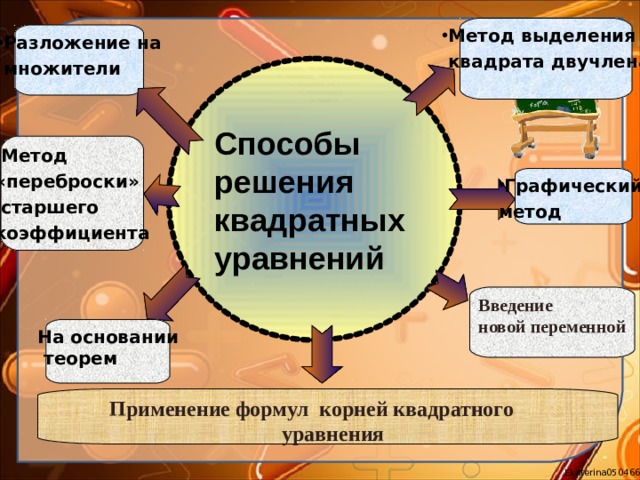
квадрата двучлена
множители
Способы
решения
квадратных
уравнений
«переброски»
старшего
коэффициента
метод
Введение
новой переменной
На основании
теорем
Применение формул корней квадратного
уравнения

Энциклопедия квадратного уравнения
 0, то " width="640"
0, то " width="640"
Неполные квадратные уравнения:
Если корней нет.
Если 0, то

Полное квадратное уравнение
Применение формул
корней квадратного
уравнения

Письмо из
прошлого
Знаешь ли ты, что…
Квадратные уравнения возникли очень давно. Еще в Вавилоне около 2000 лет назад до нашей эры. В 1202 году итальянский ученый Леонард Фибоначчи изложил формулы квадратного уравнения. И лишь в 17 веке, благодаря Ньютону и Декарту эти формулы приняли современный вид.
Понятие "дискриминант" придумал английский ученый Сильвестр, который называл себя "Математическим Адамом" за то, что придумывал множество терминов.
Сильвестр Джеймс Джозеф

Что общего между понятием “ светофор ” и “ дискриминант ” ?
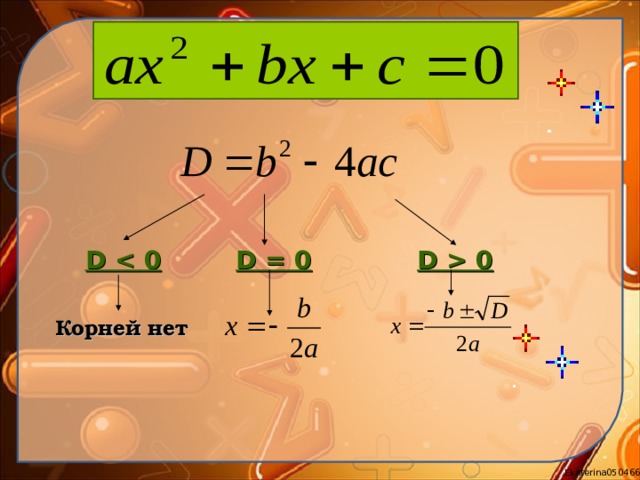 0 D = 0 D 0 Корней нет " width="640"
0 D = 0 D 0 Корней нет " width="640"
D 0
D = 0
D 0
Корней нет
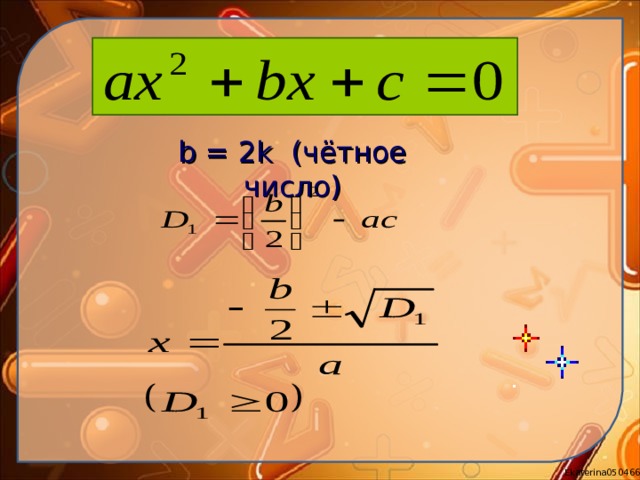
b = 2k ( чётное число)

Мнемонические правила:
Из « Радионяни »:
«Минус» напишем сначала, Рядом с ним p пополам, «Плюс-минус» знак радикала, С детства знакомого нам. Ну, а под корнем, приятель, Сводится всё к пустяку: p пополам и в квадрате Минус прекрасное q .
- Из « Радионяни » (другой вариант):
p , со знаком взяв обратным, На два мы его разделим, И от корня аккуратно Знаком «минус-плюс» отделим. А под корнем очень кстати Половина p в квадрате Минус q — и вот решенья, То есть корни уравненья.

Теорема Виета
x 1 и х 2 – корни уравнения
x 1 и х 2 – корни уравнения

Мнемоническое правило
Познакомили поэта С теоремою Виета Оба корня он сложил минус p он получил а корней произведенье дает q из уравнения

Метод выделения квадрата двучлена.
Суть метода: привести квадратное уравнение общего вида к неполному квадратному уравнению.

Метод разложения на множители
привести квадратное уравнение общего вида к виду
А(х) · В(х)=0,
где А(х) и В(х) – многочлены относительно х.
Цель:
Способы:
- Вынесение общего множителя за скобки;
- Использование формул сокращенного умножения;
- Способ группировки.

Введение новой переменной.
Умение удачно ввести новую переменную – важный элемент математической культуры. Удачный выбор новой переменной делает структуру уравнения более прозрачной.
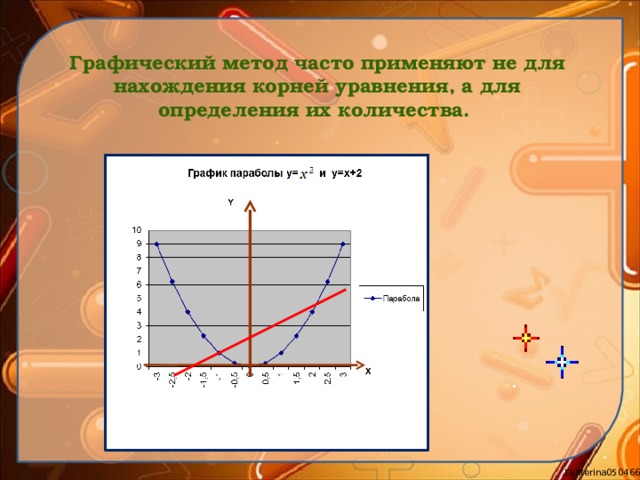
Графический метод часто применяют не для нахождения корней уравнения, а для определения их количества.

Метод «переброски» старшего коэффициента.
Корни квадратных уравнений
и
связаны соотношениями
и

На основании теорем:
Если в квадратном уравнении a+b+c=0 , то один из корней равен 1, а
второй по теореме Виета равен
Если в квадратном уравнении a+c=b , то один из корней равен (-1),
а второй по теореме Виета равен

4. b - нечётное
1. в,с=0
ах 2 =0
ах 2 + bx +с=0
№ уравнения
1
100x 2 + 53x – 153 = 0
2
№ метода
20 x 2 - 6x = 0
3
299x 2 + 300x + 1 = 0
4
3x 2 - 5x + 4 = 0
5
7x 2 + 8x + 2 = 0
6
7
35x 2 – 8 = 0
4x 2 – 4x - 3 = 0
8
(x – 8) 2 – (3x + 1) 2 = 0
9
4(x – 1) 2 + 0,5(x – 1) – 1 = 0
10
12x 2 = 0
2. с=0
ах 2 +вх=0
5. b - чётное
ах 2 + bx +с=0
3. в=0
ах 2 +с=0
6. Теорема Виета.
7. Метод выделения квадрата двучлена.
8. Метод «переброски» старшего коэффициента.
9. Т1 или Т2.
10. Метод разложения на множители.
11. Метод введения новой переменной.

Математик немного поэт. Т. Вейерштрасс

Мыслить последовательно, судить доказательно, опровергать неправильные выводы должен уметь всякий: физик и поэт, тракторист и химик.
Э. Кольман

Реши задачу
Задача знаменитого индийского математика XII века Бхаскара.
- Обезьянок резвых стая Всласть поевши, развлекалась. Их в квадрате часть восьмая На поляне забавлялась. А двенадцать по лианам Стали прыгать, повисая: Сколько ж было обезьянок, Ты скажи мне в этой стае?

В ы в о д
- Наши исследования подтвердили гипотезу проекта. Весь собранный и исследованный материал поможет нам в подготовке к ОГЭ. А так же данный проект можно использовать на уроках математики при изучение тем связанных с квадратным трехчленом. Мы же продолжим дальнейшие изучения квадратного трехчлена и его применение.

Мало иметь хороший ум, главное – хорошо его применять. Р.Декарт

Используемые источники
Фон http://www.kukud.net/fengjing/UploadFiles_8688/201011/2010113010143481.jpg
Сова http://www.gymnasium31.perm.ru/images/sova2014.jpg
Школьная доска http://mathmat.wikispaces.com/file/view/uslu-sayilar.jpeg/228156620/292x317/uslu-sayilar.jpeg
Автор шаблона: Елисеева Е. С., учитель начальных классов МАОУ «СОШ №17»г. Улан-Удэ республики Бурятия

- Исследовательская работа на тему:
О квадратном трёхчлене замолвите слово
- Выполнили: ученики 8б класса Омарова Халида и Будзан Карина.
- Руководитель: Авраменко Любовь Дмитриевна, учитель математики.

















 0, b и c – любые, сформулировал Брахмагупта (VII в. н. э.). Брахмагупта еще не знал, что квадратное уравнение может иметь и отрицательный корень. Бхаскара Ачарья (XII в .) сформулировал, соотношения между коэффициентами уравнения. Составил много задач. " width="640"
0, b и c – любые, сформулировал Брахмагупта (VII в. н. э.). Брахмагупта еще не знал, что квадратное уравнение может иметь и отрицательный корень. Бхаскара Ачарья (XII в .) сформулировал, соотношения между коэффициентами уравнения. Составил много задач. " width="640"





 0, то " width="640"
0, то " width="640"



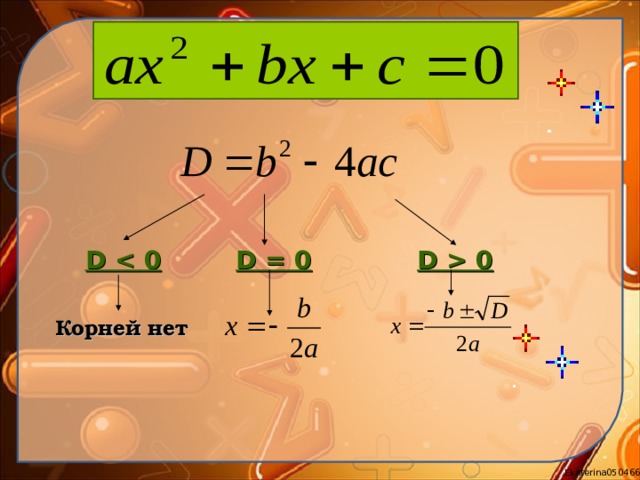 0 D = 0 D 0 Корней нет " width="640"
0 D = 0 D 0 Корней нет " width="640"