Исследовательская работа "Ох, уж эти смеси, сплавы,концентрация и проценты"

НПК «Шаг в будущее»

«Ох, уж эти смеси, сплавы,

концентрация и проценты …»

Эпиграф

«Если вы хотите научиться плавать, то смело входите в воду,

а если хотите научиться решать задачи, то решайте их.»

Дьёрдь По́йа

Объект исследования: задачи на смеси, сплавы и концентрацию

Предмет исследования: многообразие задач, методы и приемы их решения

Цель работы: создание более полного представления о методах решения задач данного типа и научиться решать этими методами

Гипотеза: если я буду вооружен необходимым теоретическим материалом по данной теме, тогда и решения подобных задач не вызовут у меня затруднения, и ее решение будет для меня как объект конструирования и изобретения

Задачи исследования:

• Изучить исторический и теоретический материал по интересующему вопросу
• Раскрыть некоторые методы решения задач на концентрацию, смеси и сплавы.
• Выявить практическое применение таких задач.
• Определить план дальнейшей работы над темой.

Задача «В парикмахерской»

Может ли алгебра понадобиться в парикмахерской?

Оказывается, такие случаи бывают. Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:

-Не поможете ли нам разрешить задачу, с которой мы никак не справимся?

- Уж сколько раствора испортили из-за этого!- добавил другой

- В чем задача ?

- У нас имеется два раствора перекиси водорода: 30%- ный и 3 % -ный. Нужно их смешать так, чтобы составился 12% -ный раствор. Не можем подыскать правильной пропорции…

Мне дали бумажку, и требуемая пропорция была найдена.

Она оказалась очень простой. Какой именно ?

Немного о Карле Пирсоне…

выдающийся английский математик

Выо Пирсоне …

• Дата рождения: 27 марта 1857
• Место рождения: Англия, Лондон
• Дата смерти: 27 апреля 1936 (79 лет)
• Страна:  Великобритания
• Научная сфера: математика, статистика
• Награды и премии: Медаль Дарвина (1898)

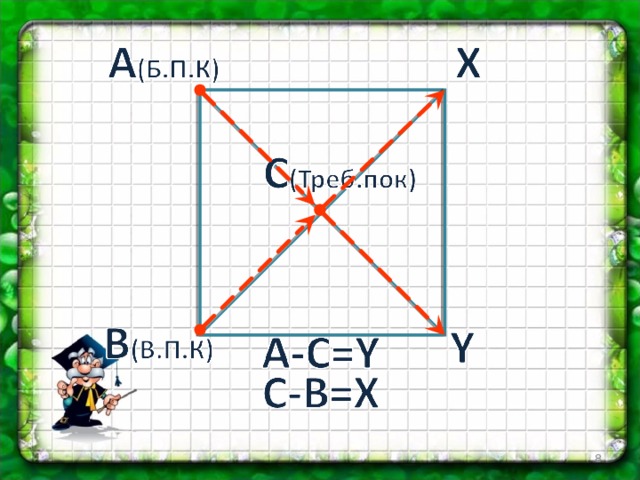
При решении задач на растворы с разными концентрациями чаще всего применяют квадрат Пирсона.

При расчётах записывают одну над другой массовые доли растворённого вещества в исходных растворах, справа между ними – его массовую долю в растворе, который нужно приготовить, и вычитают по диагонали из большего меньшее значение.

Разности их вычитаний показывают массовые доли для первого и второго растворов, необходимые для приготовления нужного раствора.

ω 1 ω 3 — ω 2

ω 3

ω 2 ω 1 — ω 3

Немного о Леонтии Магницком…

выдающийся русский математик

Выо Пирсоне …

• Дата рождения: 19 июня

1669 год

Место рождения: город Осташков, Тверская область

• Дата смерти: 13 октября 1739 (70 лет)
• Страна:  Российская Империя
• Научная сфера: математика

b или c a , то задача неразрешима, ибо, смешивая дешевые вещества, дорогое не получишь). Поэтому можно считать, что a c b .Смешиваем один фунт первого вещества и q второго. В результате получится 1+ q фунтов вещества стоимостью a + bq гривен. Один фунт смеси должен стоить с гривен. Значит должно выполняться равенство a + bq = c *(1+ q ). Отсюда находим q =( c - a )/( b - c ) или ( b - c ):( c - a ). Именно этот соотношение дает старинный способ a b - c c b c – a " width="640"

Старинный способ решения

Предположим, что смешиваются два вещества – первое стоимостью а гривен за фунт и второе стоимостью b гривен за фунт. Желательно получить вещество стоимостью с гривен за фунт. Будем считать, что а b

( если с b или c a , то задача неразрешима, ибо, смешивая дешевые вещества, дорогое не получишь).

Поэтому можно считать, что a c b .Смешиваем один фунт первого вещества и q второго. В результате получится 1+ q фунтов вещества стоимостью a + bq гривен. Один фунт смеси должен стоить с гривен. Значит должно выполняться равенство a + bq = c *(1+ q ). Отсюда находим q =( c - a )/( b - c ) или ( b - c ):( c - a ).

Именно этот соотношение дает старинный способ

• a b - c
• c
• b c – a

У некоторого человека были продажные масла: одно ценою 10 гривен за ведро, а другое 6 гривен за ведро. Захотелось ему сделать из этих двух масел, смешав их , масло ценою 7 гривен за ведро . Какие части этих двух масел нужно взять , чтобы получить ведро масла стоимостью 7 гривен ?

 

Решение: 3/4-дешевого масла

6 3

 

7

10 1 1/4-дорогого масла

Проверка: 1/4* 10+3/4*6=28/4=7 гривен

Решение задачи «В парикмахерской»

. Пусть для составления 12%-ной смеси требуется взять x граммов 3%-ного раствора и y граммов 30% -ного раствора. Тогда в первой пропорции содержится 0,03 x граммов чистой перекиси водорода, во второй 0,3 y , а всего

0,03 x + 0,3 y

В результате получается ( x + y ) граммов раствора, в котором чистой перекиси должно быть 0,12 ( x + y )

Имеем уравнение

0,03 x + 0,3 y =0,12 ( x + y )

Из этого уравнения находим x =2 y , т.е. 3%- ного раствора надо взять вдвое больше.

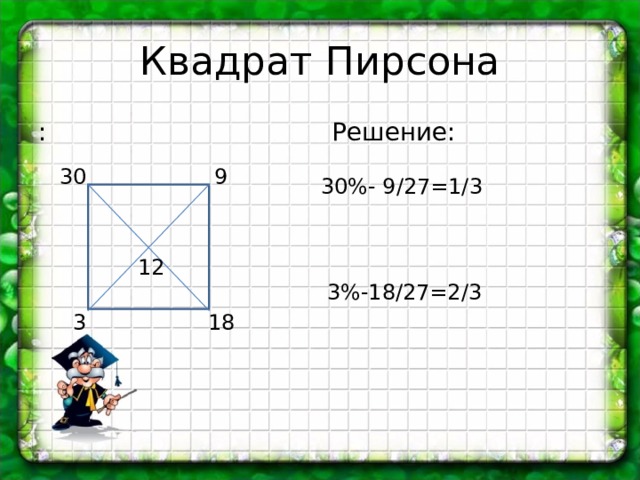
Квадрат Пирсона

:

Решение:

30

9

30%- 9/27=1/3

12

3%-18/27=2/3

3

18

Старинный метод Магницкого:

3 18

12

30 9

3%- 18/27=2/3

30%-9/27=1/3

Метод стаканчиков

=

+

Допустим X г

0,03 %

Y г

0,3 %

X+Y г

0,12 %

Тогда 0,03x + 0,3y = 0,12(x+y)

то х = 2y

Ответ: x=2y

Вывод: сравнив полученные результаты, я пришла к выводу, что решение задач на проценты различными способами дают один и тот же результат. Итак, гипотеза оказалась верной.

Спасибо за внимание!