Исследовательская работа "Пальцевый счёт"

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа № 2

г. Нижний Ломов

На научно-практическую конференцию «Старт в науку»

«Пальцевый счёт»

Работу выполнила:

Попова Виктория,

ученица8 «к» класса

МБОУ СОШ № 2

г. Нижний Ломов

руководитель:

учитель математики,

Буренкова Г.Н.

г. Нижний Ломов, 2020

Содержание:

Введение…………………………………………………………………… 3

1. Как люди научились считать……………………………………………4

1.1 Что такое пальцевый счет? ……………………………………………4

2. Счёт на пальцах у разных народов……………………………………...6

2.1 Арабско-восточноафриканский счёт. …………………………………7

2.2 Китайский счёт. ……………………………………………………..….8

2.3 Континентальный европейский счёт. ………………………………..10

2.4 Русский счёт. ……………………………………………………………10

3. Таблица умножения на пальцах. ………………………………………..12

Заключение…………………………………………………………………13

Литература…………………………………………………………………..14

Приложения………………………………………………………………….15

Введение

Можно ли представить себе мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны, если бы не наука о числах.

Две стихии господствуют в математике – числа и фигуры с их бесконечным многообразием свойств и взаимосвязей. В моей работе предпочтение отдано стихии чисел и действий с ними.

С глубокой древности накапливалось все больше сведений о числах. Начатки математических знаний обнаруживаются уже примерно за 4 тыс. лет до н.э. Об этом свидетельствуют дошедшие до нас египетские папирусы, вавилонские таблички, где встречаются решения арифметических, геометрических и алгебраических задач.

В 3 в. до н.э. Архимед нашёл способ определения площадей, объёмов и центров тяжести простых фигур. Во 2 в. до н.э. Птолемей изложил основы тригонометрии, дал таблицы синусов. Учёные народов Востока и Западной Европы делали сложнейшие математические вычисления без технических приспособлений.

Сейчас, на этапе стремительного развития информатики и вычислительной техники, современные школьники не хотят утруждать себя счетом в уме. Поэтому я сочла важным показать не только то, что сам процесс выполнения действия может быть важным, но и интересным занятием.

Мне показалось интересным разобраться в древних способах счета. Теперь я понимаю, насколько мудры были древние математики. Изучать эти материалы действительно очень увлекательно. Подобные сведения не содержатся в школьных учебниках.

Объектом исследования является счет на пальцах.

Предметом исследования выступает процесс вычисления.

Цель: изучить приемы вычислений на пальцах

Задачи:

• раскрыть историю возникновения счета;

• описать старинные способы вычислений;

• рассмотреть некоторые приемы вычисления на пальцах и овладеть некоторыми из них.

Для того чтобы выяснить, знают ли современные школьники способы выполнения арифметических действий при помощи пальцев рук был проведен опрос №1. И на вопрос о том хотели бы они о них узнать, был проведен опрос №2. Всего опрошено 26 учащихся моего класса .После проведенных исследований большая часть заинтересовалась новыми для них способами вычисления , но только 1/3 из них овладели некоторыми методами вычисления на пальцах , а точнее умножением на пальцах .Также для своей работы я взяла группу для наблюдения , в которую входили дети 4-6 лет.

Я пришла к выводу, что по этапам его развития, накопления знаний и

навыков можно сделать много интересных умозаключений об этапах

развития человека Мне было интересно наблюдать за тем,

как малыши учатся считать, а потом сопоставлять этапы его математического

развития с историческими этапами развития такой великой науки, как математика.

1. Как люди научились считать.

Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Постепенно возникало необходимость отвечать на жизненно важные вопросы: поскольку плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас; сколько нужно сделать ножей и т.п. Таким образом, сам не замечая, человек начал считать и вычислять.

Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов - одного птенца и т. д. Научившись выделять один предмет из множества других, говорили: "один", а если их было больше - "много"

Первые представления маленьких о числах сводились примерно к

следующей "математической системе мира": один, два, много, очень много и

самая обидная цифра - нет или отсутствие чего-нибудь. Я прочитал

соответствующий раздел в детской энциклопедией и выяснил, что древние

люди в самом начале своего эволюционного развития примерно так и

считали. Первой системой счёта у наших далеких предков являлось противопоставление понятий «один» – «много».

Лишь постепенно человек научился считать до трех, затем до пяти и до десяти и т.д. Название каждого числа отдельным словом было великим шагом вперед.

Для счета люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах 20.

Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счета. При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.

1. Что такое пальцевый счет?

Сейчас вряд ли кого удивишь карманным калькулятором, которым мы пользуемся каждый раз, когда нужно быстро и точно произвести какие-то расчеты. До калькулятора для вычислений использовались арифмометры - механические счетные машинки, счеты, счетные палочки. Древнейшим же счетным инструментом, данным человеку самой природой, была его собственная рука.О том, что для счета первобытный человек пользовался в основном пальцами, говорят имена числительные во многих языках. Кисть руки (славянское «пясть») - основа п роисхождения числительного «пять» в русском языке. То же во м ногих других языках. Например, малайское «лима» — это и «рука», и «пять». многих языках. Кисть руки (славянское «пясть») - основа п роисхождения числительного «пять» в русском языке. То же во м ногих других языках. Например, малайское «лима» — это и «рука», и «пять».

Известный русский путешественник Н. Миклухо-Маклай описал, как пользуются пальцевым счетом туземцы Новой Гвинеи — папуасы. Папуас загибает один за другим пальцы руки, повторяя: «бе, бе, ...». Загнув все пальцы, он говорит: «ибон-бе» (рука). Переходит на другую руку; загнув все пальцы, произносит: «ибон-али» (две руки). Далее переходит на ноги и поочередно говорит: «самба-бе» (одна нога), «самба-али» (две ноги). Если собственных рук и ног не хватает, папуас пользуется чужими конечностями.

От пальцевого счета пошли пятеричная система счисления (одна рука), десятеричная (две руки), двадцатиричная (пальцы рук и ног).

Полное описание пальцевого счета составил ирландский монах Беда Достопочтенный, живший в VII - VIII веках новой эры. Он подробно изложил способы представления на пальцах различных чисел вплоть до миллиона.

Кое-где пальцевый счет сохранился даже сегодня. Например, на крупнейшей в мире чикагской хлебной бирже маклеры на пальцах, не произнося ни единого слова, сообщают о предложениях, запросах, ценах на товары. Кроме этого, до сих пор родители обучают своих детей счету на пальцах, используя при этом считалочки.

Но иногда такой системой счисления

пользуются и современные люди, например, отмечая зарубками количество

прошедших дней, или карандашом отмечая черточками в тетради количество

проданных товаров. [2] Моя мама так иногда записывает количество

набранных петель, когда вяжет на спицах сложный узор, и ей важно не

сбиться со счета. Но это удобно, пока числа небольшие.

Я обратил внимание на то, что моему братику больше всего нравилось

считать на пальцах. Это объяснялось просто: такие счеты всегда под рукой, а

точнее на руках, и их весьма затруднительно потерять. Гораздо легче и

удобнее воспользоваться ими, чем подбирать для счета 10 подходящих

предметов: палочек, камешек, листиков и т.п. Вероятно, так же рассуждали и

древние люди. До сих пор в языке есть выражения, говорящие об этом:

"посчитать на пальцах одной руки", "объяснить на пальцах", "сосчитать на пальцах", "знать, как свои пять пальцев" и т.д. Сама природа предоставила

2. Счёт на пальцах у разных народов.

Известные средневековые математики рекомендовали в качестве вспомогательного средства именно пальцевой счет, допускающий довольно эффективные системы счета.

В разных странах и в разные времена считали по-разному.
Несмотря на то, что у многих народов кисть руки является синонимом и фактической основой числительного "пять", у различных народов при пальцевом счете от одного до пяти указательный и большой пальцы могут иметь разные значения.

У итальянцев при счете на пальцах рук большой палец обозначает цифру 1, а указательный - цифру 2; когда же считают американцы и англичане, указательный палец означает цифру 1, а средний - 2, в этом случае большой палец представляет цифру 5.

А русские начинают счет на пальцах, первым загибая мизинец, и заканчивают большим пальцем, обозначающим цифру 5,при этом указательный палец сопоставлялся с цифрой 4. Но когда показывают количество, выставляют указательный палец, затем средний и безымянный.

Североевропейский пальцевой счет позволял показывать пальцами одной руки, складываемыми в различные комбинации, все числа от 1 до 100. Причем большим и указательным пальцами изображались десятки, остальными тремя - единицы.
Например, число 30 получалось, когда большой и указательный пальцы левой руки были соединены в кольцо. Для того чтобы изобразить число 60, большой палец нужно согнуть и как бы склонить его перед указательным, нависающим над ним. Чтобы показать число 100, нужно было прижать выпрямленный большой палец снизу к указательному и отвести остальные три пальца в сторону.

В древнерусской нумерации единицы назывались "перстами", десятки - "суставами", а все остальные числа - "сочислениями". Счет парами вплоть до середины XVIII века всегда занимал важное место в жизни россиян, поскольку имел качественное происхождение - пара рук, ног, глаз и пр. Недаром говорили: "два сапога - пара", "двугривенный" и т.д. Четверичная ситема счета основана на "перстах" руки, не считая большого пальца. Большой - вовсе не "перст", он "палесъ"! - в этой системе счисления означал конец счета, то есть являлся эквивалентом нуля.

Счет восьмерками также основан на пальцевом счете и, по сути, является сочетанием двоичной и четверичной систем. Элементы восьмеричной системы существовали на Руси еще в начале XX столетия. Это и восьмиконечный крест, который использовали староверы, и восьмиголосное церковное пение, и название русской питейной меры - "осьмушки", получаемой в результате последовательного троекратного деления пополам.

Пальцевой счет девятками является, пожалуй, самым распространенным русским народным способом умножения на пальцах с помощью, так называемых девятериц - своеобразной таблицы умножения, обозначающей девятилетние сроки человеческой жизни.

Однако окончательно эта система счисления прижилась в России вместе с реформами Петра I, пришедшими к нам из Европы.

Как я выяснил позже, на пальцах можно не только считать, но и показывать

различные цифры. К моему великому изумлению, на пальцах можно

показывать и двухзначные и даже трехзначные цифры. У разных народов

создавались и разрабатывались точные системы обозначения чисел на

пальцах рук. На этом рисунке показана подобная система, широко применявшаяся в Европе.

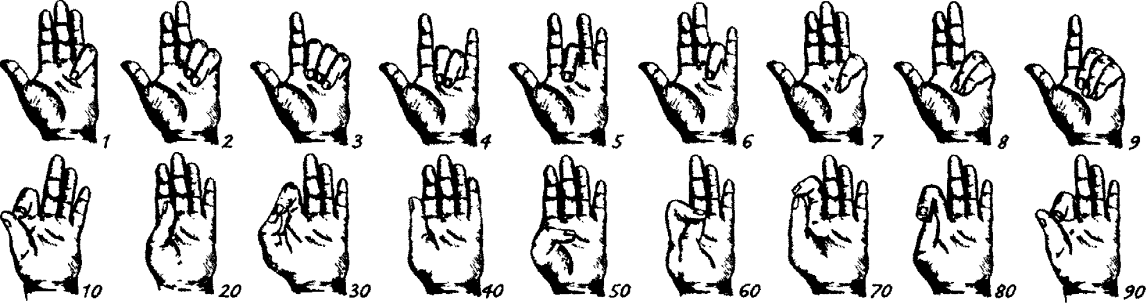
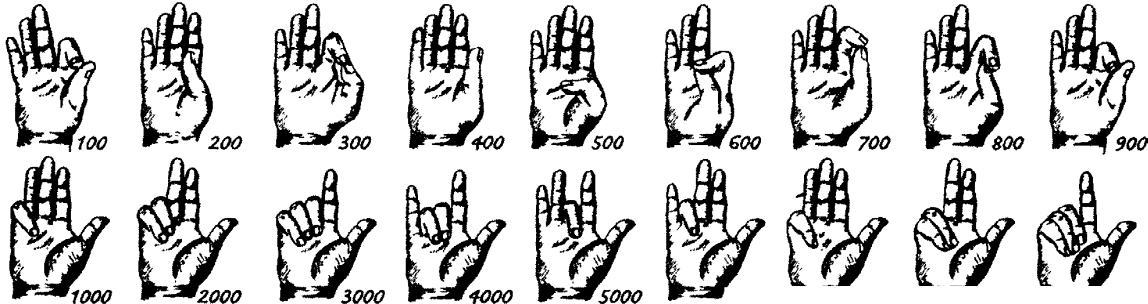
Таким образом, пальцевой счет позволял показывать пальцами одной руки,

складываемыми в различные комбинации, все числа от 1 до 1000. Причем

большим и указательным пальцами изображались десятки, остальными тремя

- единицы. Например, число 30 получалось, когда большой и указательный

пальцы левой руки были соединены в кольцо. Для того чтобы изобразить

число 60, большой палец нужно согнуть и как бы склонить его перед

указательным, нависающим над ним. Чтобы показать число 100, нужно было

прижать выпрямленный большой палец снизу к указательному и отвести

остальные три пальца в сторону. [5] Этой системой или ее разновидностями

пользуются и сейчас. Их активно применяют в биржевой торговле. Я обратил

внимание на то, что во время торгов биржевые маклеры активно

жестикулируют. Только потом я понял, что они могут показывать на пальцах различные цифры

.2.1 Арабско-восточноафриканский счёт.

В течение длительного времени на территории Арабского халифата и стран, возникших после его распада, в торговых операциях использовался римский пальцевый счёт, ещё в XIV веке арабские и персидские документы свидетельствуют о хорошем знании арабами римской системы счёта, сходной с той, которая была записана Бедой Достопочтенным в Европе начала VIII века. Особенностью этого счисления стала смена рук, означающих десятки и сотни, в соответствии с системой арабского письма справа-налево. Таким образом, правая рука стала означать сотни, а левая — единицы и десятки. Впоследствии, на восточных базарах и в портах Красного моря и восточного побережья Африки, торговцы выработали собственный оригинальный математический язык жестов. Покупатель и продавец, во избежании нечистоплотных посредников, конкурентов и нежелательных свидетелей, тайно договариваются о цене, накрыв свои руки тканью и касаясь ладоней друг друга по определённым правилам.

Прикосновение к вытянутому указательному пальцу продавца, в зависимости от цены и используемых денежных единиц, будет означать 1, 10 или 100. Одновременное прикосновение к двум, трём или чётырём пальцам продавца будет означать соответственно 2 (20, 200), 3 (30, 300) или 4 (40, 400). Касание открытой ладонью указывает на число 5, 50 или 500. Дотронуться до мизинца означает 6, 60 или 600, безымянный палец — 7, 70 или 700, средний палец — 8, 80 или 800, согнуть указательный палец — 9, 90 или 900, коснуться Большого пальца — 10, 100 или 1000. При этом счислении может соблюдаться последовательность числовых степеней, например число 78 задаётся касанием безымянного пальца продавца, а затем — его среднего пальца. Постукивание по указательному пальцу продавца в направлении от среднего сустава к кончику пальца — предложение о снижении цены вдвое (1/2), на четверть (1/4) или на восьмую часть (1/8) от первоначальной. Постукивание по указательному пальцу от основания пальца до его среднего сустава — будет являться надбавкой половины (1/2) от предложенной цены, или 1/4, или 1/8. Если перед указанием дробной степени указывается целое число, то оно умножается на дробную степень.

2.2 Китайский счёт.

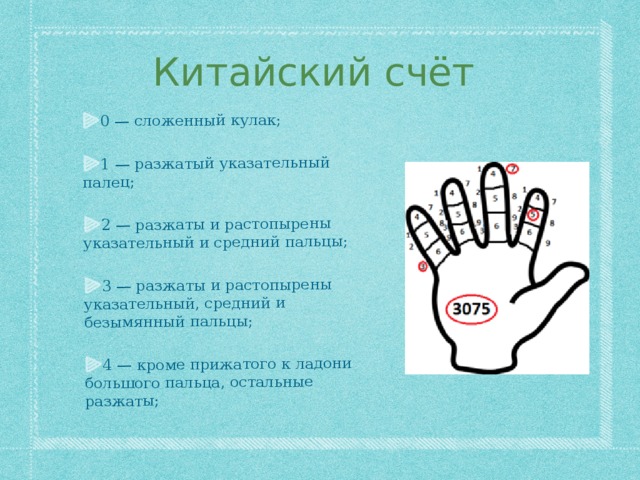
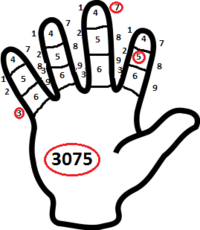Китайская позиционная десятичная система счёта с примером (выделено красным)

Китайский метод счёта основан на количестве и символике пальцев. Используя этот метод, на двух руках можно посчитать до 20. Стоит заметить, что в некоторых провинциях жесты могут отличаться.

0 — сложенный кулак;

1 — разжатый указательный палец;

2 — разжаты и растопырены указательный и средний пальцы;

3 — разжаты и растопырены указательный, средний и безымянный пальцы;

4 — кроме прижатого к ладони большого пальца, остальные разжаты;

5 — открытая ладонь;

6 — выпрямлены мизинец и большой палец, остальные — сжаты в кулак;

7 — большим палец вместе с указательным и средним сложены в щепоть;

8 — выпрямлены указательный и большой пальцы, остальные — сжаты в кулак;

9 — указательный и большой изогнуты в виде буквы «С», остальные — сжаты в кулак;

10 — три варианта. Первый: рука сжимается в кулак; второй: указательные пальцы обеих рук пересекаются; третий: выпрямленный средний палец заводится за выпрямленный указательный, остальные — сжаты в кулак.

Древнекитайская позиционная десятичная система счёта по двум рукам является наиболее сложной из существующих подобных, но при всём том позволяет показать числа от 1 до 99 999 999. На обеих руках фалангам каждого пальца задаются цифровые значения от 1 до 9: причём задействуется пространство как посреди фаланги, так и по бокам. Роль указателя играют ногти больших пальцев. Каждый палец имеет собственную разрядность, как на абаке: указательный палец правой руки — означает единицы, средний палец — десятки, безымянный — сотни и т. д. Переход от пальца к пальцу характеризуется последовательным повышением разряда. Пропуск имеет значение нуля.

2.3 Континентальный европейский счёт.

У народов континентальной Западной Европы, таких, как немцы или французы, разжатый большой палец представляет собой начало исчисления (число 1). Затем разжимается указательный палец (число 2) и так далее — до мизинца (число 5).

В некоторых европейских странах, а зачастую и во Франции, альтернативный метод подсчёта проводится путём сгибания пальцев в порядке: большой, указательный, средний, безымянный и мизинец.

2.4 Русский счёт.

Русский счёт на пальцах до десяти начинается с загибания мизинца левой руки и последовательно ведётся до загнутого большого пальца правой руки. Но когда требуется наглядно показать количество, рука сжимается в кулак и сначала разжимается указательный палец, затем средний, безымянный, мизинец и большой.

Рисунок 2. "Счет дюжинами"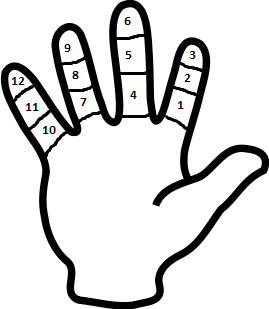

Из других способов счисления по пальцам был распространён «счёт дюжинами» (двенадцатеричная система) (Рис.2) , употреблявшийся в торговле Новгородской Счет дюжинами вёлся большим пальцем по фалангам остальных четырёх пальцев правой руки и начинался от нижней фаланги указательного пальца, а заканчивался верхней фалангой мизинца.

3. Таблица умножения на пальцах.

Особенно сложны и трудны были в старину действия умножения и деления -- особенно последнее. «Умноженье -- мое мученье, а с делением -- беда», -- говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления -- приемы один другого запутаннее, твердо запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.

Спешу предупредить, что метод рассказывает об умножении чисел 6, 7, 8, 9. По умолчанию предполагается, что умножать до пяти вы умеете.

Итак, правила счёта:Один загнутый палец – это число 6, два пальца – 7, три пальца – число 8, четыре пальца – число 9.

Пример.

Умножаем 6х6.

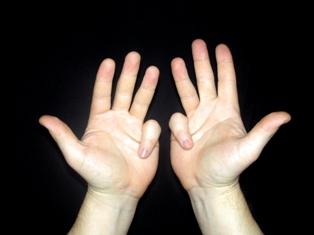
Загибаем по пальцу на обеих руках. Не согнутые пальцы умножаем друг на друга. 4х4=16. Согнутые принимаем за десятки, и складываем. Это 20. 20+16=36. Итого 6х6=36

Умножаем. 6х7.

Не согнутые пальцы умножаем друг на друга. 4х3=12. Согнутые принимаем за десятки, и складываем. Это 30. 30+12=42. Итого 6х7=42

Умножаем 7х7

Не согнутые пальцы умножаем друг на друга. 3х3=9. Согнутые принимаем за десятки, и складываем. Это 40. 40+9=49. Итого 7х7=49

Умножаем 7х8

Не согнутые пальцы умножаем друг на друга. 3х2=6. Согнутые принимаем за десятки, и складываем. Это 50. 50+6=56. Итого 7х8=56

Умножаем 8х8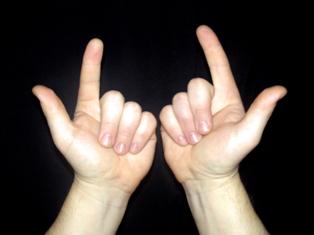

Не согнутые пальцы умножаем друг на друга. 2х2=4. Согнутые принимаем за десятки, и складываем. Это 60. 60+4=42. Итого 8х8=64

Умножаем 8х9

Не согнутые пальцы умножаем друг на друга. 2х1=2. Согнутые принимаем за десятки, и складываем. Это 70. 70+2=72. Итого 8х9=72

Умножаем 9х9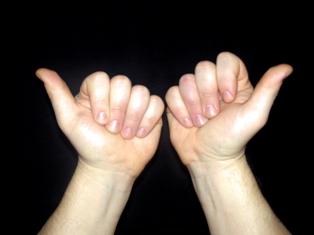

Не согнутые пальцы умножаем друг на друга. 1х1=1. Согнутые принимаем за десятки, и складываем. Это 80. 80+1=81. Итого 9х9=81

ия над многозначными числами в двоичной системе выполняются по тем же правилам, что и в десятичной.

Сложим числа 101101 и 10100. Запишем одно число под другим, соблюдая разряды:

101101 1101

+ 10100  110

1000001 11010

1101­­­­___

100110

Правда, эта система очень проста, и по сравнению с десятичной громоздка, но у нее есть ряд преимуществ. Расскажу только об одном.

Предположим, что для обозначения чисел мы используем пальцы рук. Так поступают, например, судьи баскетбольных матчей, показывая «на пальцах» номер игрока, получившего персональное замечание. Если номер игрока не больше десяти, то судья просто показывает соответствующее число пальцев; если же номер больше десяти, то судья показывает пальцы одной руки, зажатые в кулак – это десяток, и добавляет число пальцев другой руки – единицы. Так он может показывать номера 11, 12, 13, 14. 15. А как быть, если игроков больше (т.е , если матч не баскетбольный, а, например, футбольный)? Можно использовать не десятичную систему счисления, а двоичную, ведь пальцами только одной руки можно показывать любое число от единицы до тридцати одного включительно.

Заключение.

Узнав все эти занимательные факты, я внимательно посмотрел на мои руки.

Я знала, что именно руки сыграли важную роль в эволюционном развитии

человека, а самую главную – большой палец и его строение. Оно позволяло

первобытному человеку использовать орудия труда, совершенствовать их и

совершенствоваться самому. Рука - это, безусловно, одна из самых важных

частей тела человека. Раньше мне казалось, что она предназначена в

основном для того, чтобы брать какие-то предметы, переносить их, класть,

ставить, мастерить что-либо, писать, ложку держать и т.д. Я и подумать не

мог, что это самые настоящие счеты. Счеты эти человечеству подарила сама

природа. Человеку понадобились века эволюции, напряженной работы ума,

практики, наблюдений, сопоставления и анализа, чтобы так ловко научиться

ими пользоваться. Таблица умножения на пальцах оказалась для меня самым

большим и значимым открытием, которое я сделал для себя во время

подготовки данной работы . Я добросовестно пыталась ее освоить вместе со своими одноклассниками , которые проявили интерес к теме моего исследования . На это у

меня ушла целая неделя. Если мне было так сложно научиться умножать на

пальцах, то как же сложно было придумать такую уникальную систему!

Я считаю, что в век развития компьютерных технологий счет на пальцах,

разумеется, утратил свое былое значение. Вряд ли современные бизнесмены

будут совершать расчеты на пальцах или перемножать проценты, как русские

купцы в давние времена. Однако это гениальное изобретение наших предков

по-прежнему можно использовать. На мой взгляд, прямое применение

системы счета на пальцах – это сфера дошкольного образования. Глядя на младшую группу детей , я убедилась в том, что иму нравилось считать на

пальцах. Для ребенка такая система счета была простой, понятной и

наглядной. Важным положительным фактором системы счета на пальцах

является ее осязательность. Маленьким детям труднее всего понять и

представить абстрактные понятия. По большому счету число 7 или 8 для

малыша это пустой звук. Именно система счета на пальцах позволяет юному

математику «потрогать, пощупать, ощутить» эти цифры.

В этой работе была сделана попытка изучить разработанные способы счета на пальцах рук, раскрыть историю возникновения счета, описать старинные способы вычислений и показать, что современные счетные машины появились на основе способов счета на пальцах рук.

Мною сделан вывод, о том, что с помощью пальцев можно не только складывать и вычитать, но и умножать; пальцы удобны для счета в двоичной системе счисления. Изучив различные способы счета на пальцах, мы приобщаемся к истории математики.

Важным выводом изученной темы является то, что представление чисел с помощью пальцев рук в двоичной системе счисления стало основой появления вычислительной техники – компьютеров.

Тема моей работы достаточно актуальна, поскольку пальцевый счёт – занятие всегда доступное, простое и развивающее.

Мир без чисел нельзя представить прав был Пифагор: « Все есть число!»

Литература:

1. История математики с древнейших времен до начала ХIХ столетия: В 3 т. / Под ред. А. П. Юшкевича. — М.: Наука, 1970. — Т. 1.

2. Кольман Э. История математики в древности.— М., 1961.

3. Ванцян А.Г. Математика: Учебник для 5 класса. - Самара: Издательский дом «Фёдоров», 1999г.

4. Кордемский Б.А., Ахадов А.А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986г.

5. Минских Е.М. «От игры к знаниям», М., «Просвещение», 1982г.

6. Свечников А.А. Числа, фигуры, задачи. М., Просвещение, 1977г.

7. Билл Хэндли «Считайте в уме как компьютер», Минск, Попурри, 2009г.

8. /sys-schi/file15.htm

9. /mod/1/6506/hystory.html

ПРИЛОЖЕНИЯ : Сводные итоги по опросам

Торг с использованием счёта на пальцах в древнем Новгороде (фрагмент картины А. М. Васнецова «Новгородский торг», 1909 г.)

Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №2 г.Нижний Ломов.

Пальцевый счёт

Подготовила:

Попова Виктория

ученица 8«К» класса

МБОУ СОШ №2 г. Нижний Ломов

Руководитель:

Буренкова Г.Н.

учитель математики

МБОУ СОШ №2 г.Нижний Ломов

Содержание

• Объект исследования
• Предмет
• Цель
• Задачи
• Актуальность
• Виды пальцевого счёта
• Таблица умножения на пальцах

• Объект исследования

• Счет на пальцах

Предмет исследования

• Процесс вычисления

Цель

• Изучить приемы вычислений на пальцах и показать, как пальцевый счёт может пригодиться в повседневной жизни.

• ЗАДАЧИ

• * раскрыть историю создания возникновения счета
• * описать старинные способы вычислений
• * рассмотреть некоторые приемы вычисления на пальцах и овладеть некоторыми из них

Актуальность

• Доказать то, что пальцевый счёт разных народов может пригодиться в повседневной жизни.

• .

Что такое пальцевый счёт

Счёт на пальцах у разных народов

• Итальянский счет
• Арабско-восточноафриканский счёт
• Китайский счёт
• Японский счёт
• Английский счёт
• Континентальный европейский счёт
• Русский счёт
• Телесный счёт

• 0 — сложенный кулак;
• 1 — разжатый указательный палец;
• 2 — разжаты и растопырены указательный и средний пальцы;
• 3 — разжаты и растопырены указательный, средний и безымянный пальцы;
• 4 — кроме прижатого к ладони большого пальца, остальные разжаты;

Китайский счёт

• 5 — открытая ладонь; _____
• 6 — выпрямлены мизинец и большой палец, остальные — сжаты в кулак;
• 7 — большим палец вместе с указательным и средним сложены в щепоть; ______________
• 8 — выпрямлены указательный и большой пальцы, остальные — сжаты в кулак;
• 9 — указательный и большой изогнуты в виде буквы «С», остальные — сжаты в кулак;
• 10 — три варианта. Первый: рука сжимается в кулак; второй: указательные пальцы обеих рук пересекаются; третий: выпрямленный средний палец заводится за выпрямленный указательный, остальные — сжаты в кулак.

Китайский счёт

0 — сложенный кулак;

1 — разжатый указательный палец;

2 — разжаты и растопырены указательный и средний пальцы;

3 — разжаты и растопырены указательный, средний и безымянный пальцы;

4 — кроме прижатого к ладони большого пальца, остальные разжаты;

5 — открытая ладонь;

6 — выпрямлены мизинец и большой палец, остальные — сжаты в кулак;

7 — большой палец вместе с указательным и средним сложены в щепоть;

8 — выпрямлены указательный и большой пальцы, остальные — сжаты в кулак;

9 — указательный и большой изогнуты в виде буквы «С», остальные — сжаты в кулак;

10 — три варианта. Первый: рука сжимается в кулак; второй: указательные пальцы обеих рук пересекаются; третий: выпрямленный средний палец заводится за выпрямленный указательный, остальные — сжаты в кулак.

Японский счёт

В Японии счёт начинается с открытой ладони. Поджатый большой палец представляет число 1, мизинец является числом 5. Таким образом, пальцы, сложенные в кулак, указывает на число 5. Затем совершается обратное действие: число 6 обозначается разжатым мизинцем. Возврат к открытой ладони означает число 10. Однако, чтобы показать цифры другим собеседникам, используется тот же порядок, что в английской или русской традиции: выпрямленный указательный палец становится номером 1, большой палец теперь представляет число 5. Для чисел свыше пяти соответствующее количество выпрямленных пальцев другой руки прижимаются к раскрытой ладони первой. Например, число 7 отображают указательный и средний палец. Число 10 изображается двумя раскрытыми к собеседнику ладонями

Английский счёт

В англоязычных странах счёт до 5 ведётся разжатием пальцев, первоначально собранных в кулак, начиная с указательного пальца, и продолжается до мизинца (число 4). Разжатый большой палец указывает на число 5. Аналогичным образом процесс счёта продолжается на другой руке для чисел от 6 до 10. Например, число 7 указывается открытой ладонью с растопыренными пальцами одной руки и разжатыми указательным и средним пальцами другой. Чтобы указать на количество своему собеседнику, коренной житель англоговорящей страны поднимает руку или руки вверх. Например, разжатые указательный, средний и безымянный пальцы на поднятой вверх ладони будут означать число 3

Континентальный европейский счёт

У народов континентальной Западной Европы, таких, как немцы или французы , разжатый большой палец представляет собой начало исчисления (число 1). Затем разжимается указательный палец (число 2) и так далее — до мизинца (число 5)

В некоторых европейских странах, а зачастую и во Франции , альтернативный метод подсчёта проводится путём сгибания пальцев в порядке: большой, указательный, средний, безымянный и мизинец.

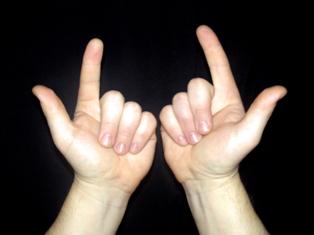
Русский счёт

Русский счёт на пальцах до десяти начинается с загибания мизинца левой руки и последовательно ведётся до загнутого большого пальца правой руки. Но когда требуется наглядно показать количество, рука сжимается в кулак и сначала разжимается указательный палец, затем средний, безымянный, мизинец и большой [2] .

Этот счёт также имеет место в странах бывшего СССР .

Телесный счёт

1 (ануси) — выпрямленный мизинец правой руки;

2 (доро) — выпрямленный безымянный палец правой руки;

3 (доро) — выпрямленный средний палец правой руки;

4 (доро) — выпрямленный указательный палец правой руки;

5 (убеи) — выпрямленный большой палец правой руки;

6 (тама) — указывание на правое запястье;

7 (унубо) — указывание на правый локоть;

8 (виса) — указывание на правое плечо;

9 (деноро) — указывание на правое ухо;

10 (дити) — указывание на правый глаз;

11 (дити) — указывание на левый глаз;

12 (медо) — указывание на нос;

13 (бее) — указывание на рот;

14 (деноро) — указывание на левое ухо;

15 (виса) — указывание на левое плечо;

16 (унубо) — указывание на левый локоть;

17 (тама) — указывание на левое запястье;

18 (убеи) — выпрямленный большой палец левой руки;

19 (доро) — выпрямленный указательный палец левой руки;

20 (доро) — выпрямленный средний палец левой руки;

21 (доро) — выпрямленный безымянный палец левой руки;

22 (ануси) — выпрямленный мизинец левой руки.

• Таблица умножения на пальцах

Умножаем 6х6

Загибаем по пальцу на обеих руках. Не согнутые пальцы умножаем друг на друга. 4х4=16. Согнутые принимаем за десятки, и складываем. Это 20. 20+16=36. Итого 6х6=36

• Таблица умножения на пальцах

Умножаем 6х7

Не согнутые пальцы умножаем друг на друга. 4х3=12. Согнутые принимаем за десятки, и складываем. Это 30. 30+12=42. Итого 6х7=42

• Таблица умножения на пальцах

Умножаем 7х7

Не согнутые пальцы умножаем друг на друга. 3х3=9. Согнутые принимаем за десятки, и складываем. Это 40. 40+9=49. Итого 7х7=49

• Таблица умножения на пальцах

Умножаем 7х8

Не согнутые пальцы умножаем друг на друга. 3х2=6. Согнутые принимаем за десятки, и складываем. Это 50. 50+6=56. Итого 7х8=56

• Таблица умножения на пальцах

Умножаем 8х8

Не согнутые пальцы умножаем друг на друга. 2х2=4. Согнутые принимаем за десятки, и складываем. Это 60. 60+4=42. Итого 8х8=64

• Таблица умножения на пальцах

Умножаем 8х9

Не согнутые пальцы умножаем друг на друга. 2х2=4. Согнутые принимаем за десятки, и складываем. Это 60. 60+4=42. Итого 8х8=64

• Таблица умножения на пальцах

Умножаем 8х9

Не согнутые пальцы умножаем друг на друга. 2х1=2. Согнутые принимаем за десятки, и складываем. Это 70. 70+2=72. Итого 8х9=72

• Таблица умножения на пальцах

Умножаем 9х9

Не согнутые пальцы умножаем друг на друга. 1х1=1. Согнутые принимаем за десятки, и складываем. Это 80. 80+1=81. Итого 9х9=81

Сводные итоги по опросам

дети младшей группа 10чел

ФИО

те ,кто знает некоторые способы выполнения арифметических действий при помощи пальцев рук

6

те, кто хотели бы подробнее узнать о способах выполнения арифметических действий при помощи пальцев рук

одноклассники 26чел

те, кто овладел некоторыми способами выполнения арифметических действий при помощи пальцев рук

10

26

итого 32 30 14

8

20

6

• СПАСИБО
• за
• внимание !!!