Исследовательская работа по математике по теме "Софизмы"

Муниципальное общеобразовательное бюджетное учреждение средняя общеобразовательная школа №8 г. Белорецк

муниципального района Белорецкий район

Республики Башкортостан

III МЕЖРЕГИОНАЛЬНАЯ НАУЧНО – ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ

«ЕВРОПА – АЗИЯ. ОТКРЫВАЯ ГОРИЗОНТЫ»

Направление исследования: «Математика»

Тема: «Математические софизмы»

Автор работы: Кривошеева Екатерина Игоревна, обучающаяся 6 А класса МОБУ СОШ №8 г. Белорецк МР Белорецкий район РБ

Руководитель: Лукманова Гульсина Хакимовна, учитель математики МОБУ СОШ №8 г. Белорецк МР Белорецкий район РБ

2018

Оглавление

Введение…………………………………………………………………..3 стр.

ГЛАВА 1 Исторические условия возникновения софизмов ……….....5 стр. 1.1 Понятие софизма. Из истории возникновения софизмов……....5 стр. 1.2 Классификация математических софизмов.………......................7 стр.

Выводы по главе 1…………………………………………………….8 стр.

ГЛАВА 2 Исследование в сфере учебной деятельности

2.1 Классификация ошибок и их причины….. ………………………9 стр.

2.2 Анализ ошибок учащихся по математике…………………….….9 стр.

Выводы по главе 2…………………………………………………...10 стр.

Заключение…………………………………..…………………………...11 стр.

Список источников литературы и интернет – ресурсов.……............12 стр. Приложение «Классификация математических софизмов с примерами » Приложение «Классификация ошибок и их причин» Приложение «Результаты исследования»

Приложение «Анализ ошибок учащихся по математике»

Приложение «Анкета»

Введение

"Правильно понятая ошибка - путь к открытию"

И. П. Павлов

Знаменитый комик Чарли Чаплин сказал: «Способность думать, подобно игре на скрипке или рояле, требует ежедневной практики». Невозможно с этим не согласиться! Мыслительная деятельность человека − своеобразный инструмент, пользуясь которым, можно добиться духовных, нравственных, научных высот. Такое понятие, как «софизм» бесспорно свидетельствует о блестяще развитом уме и логике владеющего им человека.

Актуальность исследования. Наше общество развивается большими темпами, и все больше требуются техники, инженеры, ученые, знания которых базируются на точных науках: математика, физика, химия. Но эти науки надо не только знать, но и понимать. Для лучшего усвоения математики существуют софизмы. Разбор софизмов прежде всего развивает логическое мышление, т.е. прививает навыки правильного мышления. Обнаружить ошибку в софизме - это значит осознать ее, а осознание ошибки предупреждает от повторения ее в других математических рассуждениях. Важно добиться отчетливого понимания ошибок, иначе софизмы будут бесполезны.

Целью настоящей работы как раз является показать значимость математических софизмов при изучении математики, их роль в формировании полноценной личности, способной адаптироваться в условиях современного общества.

Гипотеза: если неточно знать формулировки определений, математические формулы, правила и условия, при которых они выполняются, а также не анализировать построение чертежа к геометрической задаче, то можно получить абсурдные результаты, противоречащие общепринятым представлениям.

Задачи исследования:

• Узнать, что называют софизмами и выяснить исторические условия возникновения софизмов; выяснить, какие виды математических софизмов бывают;

• Рассмотреть влияние софизмов в математике, проанализировать и классифицировать ошибки в работах учащихся по математике;

• Научиться самой обосновывать свои ошибки и познакомить своих одноклассников с софизмами и показать, что они встречаются чаще, чем они думают, просто они об этом не задумываются.

Предмет исследования: математические софизмы.

Объект исследования: ошибки учащихся в работах по математике.

В ходе исследования решались следующие проблемные вопросы:

1. Как появились софизмы?

2. Какие виды математических софизмов бывают?

3. В каких заданиях и как делают «математические» ошибки учащиеся?

4. Как использование софизмов помогает в понимании математики?

5. Как научиться «видеть» ошибки?

Чтобы достичь своей цели, использовались такие методы исследования: изучение литературы, сбор информации, анкетирование учащихся, обработка данных, составление таблиц и диаграмм, просмотр сайтов в Интернете.

Практическая значимость: тема исследования я считаю, значима, так как понимание математики пригодится в жизни и в первую очередь для успешной учебы в школе, надо не только точно знать правила и формулы, но уметь находить свои ошибки и ошибочные рассуждения.

ГЛАВА 1 Исторические условия возникновения софизмов 1.1 Понятие софизма. Из истории софизмов.

Софизмы… Редко кто встречался с этим понятием в жизни.

В самом начале своей работы, мы выяснили, а знают ли другие школьники о софизмах. Поэтому провели с руководителем анкету, на вопросы которой ответили 40 учеников 6 классов. И я выяснила, что практически с понятием софизмов они не знакомы. Тогда мы привели примеры известных софизмов: «Дважды два равно пяти» или хотя бы: «Два равно трем». И снова лишь 17% опрошенных ответили, что слышали о них, 27 % - считают, что встречались с софизмами на уроках математики, 30 % считают, что в повседневной действительности встречаются с софизмами.

Так что же это такое?

Софизм — ложное умозаключение, которое, тем не менее, при поверхностном рассмотрении кажется правильным. Софизм основан на преднамеренном, сознательном нарушении правил логики.

Софизм - (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. (Савин А.П. Энциклопедический словарь юного математика. М.:Педагогика, 1989г.)

Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок.

Что же такое математический софизм? Математический софизм - удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. История математики полна неожиданных и интересных софизмов, разрешение которых порой служило толчком к новым открытиям. Математические софизмы приучают внимательно и настороженно продвигаться вперед, тщательно следить за точностью формулировок, правильностью записи чертежей, за законностью математических операций. Очень часто понимание ошибок в софизме ведет к пониманию математики в целом, помогает развивать логику и навыки правильного мышления. Если нашла ошибку в софизме, значит, ты ее осознала, а осознание ошибки предупреждает от ее повторения в дальнейших математических рассуждениях. Софизмы не приносят пользы, если их не понимать.

Что касается типичных ошибок в софизмах, то они таковы: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения. Нередко, ошибки, допущенные в софизме, настолько умело скрыты, что даже опытный математик не сразу их выявит. Именно в этом и проявляется связь математики и философии в софизмах. На самом деле, софизм - гибрид не только математики и философии, но и логики с риторикой. Основные создатели софизмов – древнегреческие ученые-философы, но тем не менее, они создавали математические софизмы, основываясь на элементарных аксиомах, что еще раз подтверждает связь математики и философии в софизмах. Кроме того, очень важно правильно преподнести софизм, так, чтобы докладчику поверили, а значит, необходимо владеть даром красноречия и убеждения.

Софизмы появились в Древней Греции. Они тесно связаны с философской деятельностью софистов. Однако софизмы существовали задолго до философов-софистов, а наиболее известные и интересные были сформулированы позднее в сложившихся под влиянием Сократа философских школах. Наиболее известна деятельность старших софистов, к которым относят Протагора из Абдеры, Горгия из Леонтип, Гиппия из Элиды и Продика из Кеоса.

Аристотель называл софизмами «мнимые доказательства», в которых обоснованность заключения кажущаяся и обязана чисто субъективному впечатлению.

Вот один из древних софизмов («рогатый»), приписываемый Эвбулиду: «Что ты не терял, то имеешь. Рога ты не терял. Значит, у тебя рога». Здесь маскируется двусмысленность большей посылки. Если она мыслится универсальной: «Всё, что ты не терял…», то вывод логически безупречен, но неинтересен, поскольку очевидно, что большая посылка ложна; если же она мыслится частной, то заключение не следует логически. Последнее, однако, стало известно лишь после того, как Аристотель создал логику.

Этапы возникновения софизмов

1. Первая в истории проба проведения "логической профилактики" в математике принадлежит гениальному древнегреческому математику - Эвклиду. Он был автором первого из известных сборников математических софизмов и парадоксов (сборник "Псевдарий").

2. Софистам идейно противостоял знаменитый греческий философ Сократ. Дискуссия между софистами и Сократом о существовании объективной истины зародилась приблизительно в V в. до н.э.

3. Наши дни: появление мысли о том, что человеку свойственно ошибаться, поэтому очень важно, чтобы он умел выявлять свои и чужие ошибки, учился избегать их. Действительно, чем хитрее софизм, чем искуснее замаскирована ошибка, тем больше удовлетворения приносит он тому, кто разгадал его, так как это - маленькое открытие и прекрасная школа, культура математических вычислений.

1.2 Классификация математических софизмов

Распределим некоторые софизмы, помогающие нам развить логическое мышление и проверить, насколько глубоко мы понимаем некоторые моменты курса математики.

В этом разделе работы я рассмотрю три типа математических софизмов: алгебраические, геометрические и арифметические (Приложение 1)

Арифметические софизмы — числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

Пример: «Число, которое равно другому числу, и больше его, и меньше одновременно».

Алгебраические софизмы — намеренно скрытые ошибки в уравнениях и числовых выражениях. Пример: «Дважды два равно пяти».

Геометрические софизмы — это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними. Пример: «Спичка вдвое длиннее телеграфного столба».

Выводы по главе 1

Софизмы есть смесь философии и математики, которая не только помогает развивать логику и искать ошибку в рассуждениях. Но тем не менее, в нашем современном мире, если и находятся люди, которым интересны софизмы, в особенности математические, то они изучают их как явление только со стороны математики, чтобы улучшить навыки правильности и логичности рассуждений.

Исторические сведения о софистике и софистах помогли мне разобраться, откуда же все-таки началась история софизмов. По началу, я думала, что софизмы бывают исключительно математические. Причем в виде конкретных задач, но, начав исследование в этой области, я поняла, что софистика - это целая наука, а именно математические софизмы - это лишь часть одного большого течения.

Очень важно, чтобы человек умел выявлять свои и чужие ошибки, учился избегать их.

ГЛАВА 2 Исследование в сфере учебной деятельности

2.1 Классификация ошибок и их причин.

Основные ошибки в математических софизмах (Приложение 2)

• Деление на 0;

• Неправильные выводы из равенства дробей;

• Неправильное извлечение квадратного корня из квадрата выражения;

• Нарушения правил действия с именованными величинами;

• Путаница с понятиями “равенства” и “эквивалентность” в отношении множеств;

• Не правильное использование теорем;

• Проведение преобразований над математическими объектами, не имеющими смысла;

• Неравносильный переход от одного неравенства к другому;

• Выводы и вычисления по неверно построенным чертежам;

• Ошибки, возникающие при операциях с бесконечными рядами и предельным переходом.

2.2 Анализ ошибок учащихся по математике

Чтобы показать и подтвердить значимость софизмов в жизни, мы провели исследовательскую работу в сфере учебной деятельности (Приложение 3, 5).

Данная работа была направлена: на развитие умения находить ошибку, анализировать и устранять ее; на развитие логического мышления; на формирование математической грамотности учащихся.

Исследование проводилось среди учащихся шестых классов. В 6 Б классе был проведен урок – презентация, посвященный алгебраическим софизмам по теме «Распределительное свойство умножения», а в 6 А данного урока не проводилось. Затем по этой теме была проведена самостоятельная работа. По итогам самостоятельных работ средние баллы в каждом из классов разошлись. В 6 Б классе средний балл был равен – 3,4, а в 6 А классе – 3,2. Только два учащихся (10%) 6 Б класса допустили ошибку по данной теме, когда в 6 А ошибки допустили 4 человека (21%). Все полученные данные мы оформили в виде диаграмм (приложение 3), которые наглядно показали нам различия по уровню усвоения темы самостоятельной. Таким образом, проанализировав полученные результаты, мы сделали вывод, что ученики, разобравшие варианты возможных ошибок, научились находить и устранять их. Ученики, не получившие данной информации, допустили различные ошибки по данной теме.

Также в своей работе мы провели анализ ошибок в работах учащихся 6 классов по математике. Как я уже отмечала ранее, неточное знание формулировок, правил и условий, при которых эти правила выполняются, приводят учащихся к неправильным, а иногда и абсурдным результатам.

В настоящем исследовании рассмотрели некоторые ошибки из контрольных работ обучающихся по математике (приложение 4).

Выводы по главе 2:

По результатам анализа ошибок, допущенных учащимися 6 классов в тестовых работах по математике, можно сделать вывод, что поверхностное изучении теории (а чаще её незнание) приводит к абсурдным результатам. Софизмы наглядно показывают, почему это происходит.

Понять софизм как таковой (решить его и найти ошибку) получается не сразу. Требуются определенный навык и смекалка. Что касается меня, то некоторые софизмы приходилось разбирать по нескольку раз, чтобы действительно в них разобраться, некоторые же наоборот, казались очень простыми. Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.

Заключение

Исследовать софизмы действительно очень интересно и необычно. Порой сама попадаешься на уловки софиста, на столь безукоризненность его рассуждений. Перед тобой открывается какой-то особый мир рассуждений, которые поистине кажутся верными. Благодаря софизмам можно научиться искать ошибки в рассуждениях других, научиться грамотно строить свои рассуждения и логические объяснения. Если есть желание, то можно стать искусным софистом, добиться исключительного мастерства в искусстве красноречия или просто на досуге проверить свою смекалку.

В своей работе мы доказали, что софизмы являются не просто интеллектуальным мошенничеством, а важным двигателем человеческой мысли. Показали практическое применение софизмов и их актуальность и в наше время. Мы рассмотрели математические софизмы с точки зрения их важности для изучения математики. Вот почему имеет первостепенное значение глубокое изучение школьной математики. И математические софизмы вам покажут, как важно строго соблюдать правила и формулировки теорем при логических умозаключениях.

«Решайте задачи и не бойтесь трудностей. Преодоление их вам доставит не только глубокое удовлетворение, но и большую радость, так как «в математике есть своя красота, как в поэзии и музыке» (Н.Е.Жуковский).

«Предмет математики настолько серьезен, что полезно не упустить случая сделать его немного занимательным». Б. Паскаль

Список источников литературы и интернет ресурсов:

1. Ахманов А.С., Логическое учение Аристотеля, М., 1960г.

2. Брадис В.М., Минковский В.Л., Еленев Л.К., Ошибка в математических рассуждениях, 3 изд., М., 1967г.

3. Брутян Г., Паралогизм, софизм и парадокс//Вопросы философии, 1959г. № 1 с. 56-66.

4. Гарднер Мартин. Математические головоломки и развлечения.М.: Оникс, 1994г.

5. Глейзер Г.И. История математики в школе. М.:Просвещение, 1982г.

6. Кордемский Б.А. Великие жизни в математике. М.:Просвещение, 1995г.

7. Р.Курант, Г.Роббинс. Что такое математика? М.-.МЦНМО, 2004

8. Морозов И.А., О научном значении математических софизмов// Известия научного института им. П.Ф.Лесгафта, Пг., 1919г., с. 193-207.

9. Л.Ф.Пичурин. За страницами учебника алгебры. М. -.Просвещение, 1991г.

10. Савин А.П. Энциклопедический словарь юного математика. М.:Педагогика, 1989г.

11. Софизмы http://sophisms.ucoz.ru/index/geometricheskie_sofizmy/0-9 (15.10.18г)

12. Софизмы http://sofizmy.narod.ru/ (20.10.18г)

Приложение 1

Классификация математических софизмов с примерами

Алгебраические софизмы. Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях. Приведем примеры таких софизмов.

1. «Сочетательное и переместительное свойства алгебраической суммы не имеют места» Рассмотрим сумму бесконечного числа слагаемых, поочередно равных плюс единице и минус единице, т.е. S=1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 +… (1)

И попробуем найти значение этой суммы. Сначала поступим следующим образом. Будем объединять слагаемые в пары, начиная со второго слагаемого, ставя перед каждой парой «минус», т.е. S=1 - (1 - 1) - (1 - 1) -…=1 – 0 – 0 - …= 1

Теперь переставим каждое положительное слагаемое той же суммы (1) на место отрицательного и обратно, тогда S= -1 +1 – 1 + 1 – 1 + 1 - …= -1 +(1-1)+(1-1)+…=-1+0+0+…= -1.

Итак, по-разному переставляя слагаемые суммы (1), мы пришли к различным значениям этой суммы: 1 и –1, в итоге сумма слагаемых изменяется от перегруппировки слагаемых, а сочетательное и переместительное свойства алгебраической суммы не имеют места.

Где ошибка??? Данное свойство суммы может оказаться неверным, если некоторые члены суммы сгруппированы иначе.

2. «Дважды два равно пяти»

Имеем числовое равенство (верное): 4:4=5:5. Вынесем за скобки в каждой части его общий множитель. Получим: 4(1:1)=5(1:1). Числа в скобках равны, поэтому 4=5, или 2 * 2=5.

Где ошибка? Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4:4=5:5.

3. «Отрицательное число больше положительного»

Возьмем два положительных числа а и с. Сравним два отношения:

а: (-с) и -а : с

Они равны, так как каждое из них равно –(а:с). Можно составить пропорцию:

а: (-с) = (-а) : с

Но, если в пропорции предыдущий член первого отношения больше последующего, то предыдущий член второго отношения также больше своего последующего.

В нашем случае а -с, следовательно, должно быть -ас, т.е. отрицательное число больше положительного.

Где ошибка??? Данное свойство пропорции может оказаться неверным, если некоторые члены пропорции отрицательны.

« Спичка вдвое длиннее телеграфного столба»

 Пусть  а дм- длина спички и b дм - длина столба. Разность между b и  a  обозначим через c . Имеем  b - a = c, b = a + c. Перемножаем два эти равенства по частям, находим: b² - ab = ca + c². Вычтем из обеих частей bc. Получим: b²- ab - bc = ca + c² - bc, или b(b - a - c) = - c(b - a - c), откуда b = - c, но c = b - a, поэтому b = a - b, или a = 2b.    

Где ошибка??? В выражении b(b-a-c )= -c(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.

Арифметические софизмы. Арифметика - (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы? Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда. Приведем примеры таких софизмов.

1. « 4 руб. = 40000 коп.» Возьмём верное равенство: 2руб.=200 коп. и возведём его по частям в квадрат. Мы получим: 4 руб.=40 000 коп. В чем ошибка?

В чем ошибка? Возведение в квадрат денег не имеет смысла. В квадрат возводятся числа, а не величины.

2.«Один рубль не равен ста копейкам»

Известно, что любые два неравенства можно перемножать почленно, не нарушая при этом равенства, т.е. если a=b, c=d, то ac=bd.

Применим это положение к двум очевидным равенствам

1 р.=100 коп, (1) 10р.=10*100коп.(2)

перемножая эти равенства почленно, получим 10 р.=100000 коп. (3)

и, наконец, разделив последнее равенство на 10 получим, что 1 р.=10 000 коп. таким образом, один рубль не равен ста копейкам.

Где ошибка??? Ошибка, допущенная в этом софизме, состоит в нарушении правил действия с именованными величинами: все действия, совершаемые над величинами, необходимо совершать также и над их размерностями.

Действительно, перемножая равенства (1) и (2), мы получим не (3), а следующее равенство 10 р. =100 000 к . , которое после деления на 10 дает

1 р. = 10 000 коп., (*) а не равенство 1р=10 000 к, как это записано в условии софизма. Извлекая квадратный корень из равенства (*), получаем верное равенство 1р.=100 коп.

1. «Число, равное другому числу, одновременно и больше, и меньше его»

Возьмем два произвольных положительных равных числа А и В и напишем для них следующие очевидные неравенства:

А-В и В-В. (1) Перемножив оба этих неравенства почленно, получим неравенство А*ВВ*В, а после его деления на В, что вполне законно, ведь В0, придем к выводу, что АВ. (2) Записав же два других столь же бесспорных неравенства В-А и А-А (3)

Аналогично предыдущему получим, что В*АА*А, а разделив на А0, придем к неравенству АВ. (4) Итак, число А, равное числу В, одновременно и больше, и меньше его.

Где ошибка??? Здесь совершен неравносильный переход от одного неравенства к другому при недопустимом перемножении неравенств.

Проделаем правильные преобразования неравенств. Запишем неравенство (1) в виде А+В0, В+В0. Левые части этих неравенств положительны, следовательно, умножая почленно оба эти неравенства (А+В)(В+В)0, или А-В, что представляет собой просто верное неравенство.

Аналогично предыдущему, записывая неравенства (3) в виде (В+А)0, А+А0, получим просто верное неравенство В-А.

Приложение 2

Классификация ошибок и их причин

Логические ошибки. Так как обычно вывод может быть выражен в силлогистической форме, то и всякий софизм может быть сведён к нарушению правил силлогизма. (Силлогизм - тонкий, хитрый ход (для подтверждения или доказательства чего-либо)).

Терминологические ошибки. Грамматические, терминологические и риторические источники софизмов выражаются в неточном или неправильном словоупотреблении и построении фразы (всякое quaternio terminorum предполагает такое словоупотребление);

В устную речь математиками введены такие слова как «сумма», «произведение», «разность». Так - сумма произведения два на два и пятерки, а - удвоенная сумма двух и пяти.

Более сложные софизмы проистекают из неправильного построения целого сложного хода доказательств, где логические ошибки являются замаскированными неточностями внешнего выражения. Всякое беспорядочное следование мыслей представляет частный случай этой ошибки.

Психологические причины. Бывают троякого рода: интеллектуальные, аффективные и волевые. Во всяком обмене мыслей предполагается взаимодействие между 2 лицами, читателем и автором или лектором и слушателем, или двумя спорящими. Убедительность софизма поэтому предполагает два фактора: α — психические свойства одной и β — другой из обменивающихся мыслями сторон. Правдоподобность софизма зависит от ловкости того, кто защищает его, и уступчивости оппонента, а эти свойства зависят от различных особенностей обеих индивидуальностей.

Интеллектуальные причины софизма заключаются в преобладании в уме лица, поддающегося софизму, ассоциаций по смежности над ассоциациями по сходству, в отсутствии развития способности управлять вниманием, активно мыслить, в слабой памяти, непривычке к точному словоупотреблению, бедности фактических знаний по данному предмету, лености в мышлении (ignava ratio) и т. п. Обратные качества, разумеется, являются наиболее выгодными для лица, защищающего софизм.

Аффективные причины ошибок. Сюда относятся трусость в мышлении — боязнь опасных практических последствий, вытекающих от принятия известного положения; надежда найти факты, подтверждающие ценные для нас взгляды, побуждающая нас видеть эти факты там, где их нет, любовь и ненависть, прочно ассоциировавшиеся с известными представлениями, и т. д. Желающий обольстить ум своего соперника софист должен быть не только искусным диалектиком, но и знатоком человеческого сердца, умеющим виртуозно распоряжаться чужими страстями для своих целей

Волевые причины. При обмене мнений мы воздействуем не только на ум и чувства собеседника, но и на его волю. Во всякой аргументации (особенно устной) есть элемент волевой — императивный — элемент внушения. Категоричность тона, не допускающего возражения, определённая мимика и т. п. () действуют неотразимым образом на лиц, легко поддающихся внушению, особенно на массы. С другой стороны, пассивность (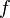) слушателя особенно благоприятствует успешности аргументации противника. Таким образом, всякий софизм предполагает взаимоотношение между шестью психическими факторами: 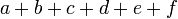. Успешность софизма определяется величиной этой суммы, в которой 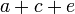составляет показатель силы диалектика, 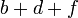есть показатель слабости его жертвы. Прекрасный психологический анализ софистики даёт Шопенгауэр в своей «Эристике» (перев. кн. Д. Н. Цертелева). Само собой разумеется, что логические, грамматические и психологические факторы теснейшим образом связаны между собой; поэтому софизм, представляющий, например, с логической точки зрения quaternio ter.

Приложение 3

Результаты исследования

Средний балл выполнения самостоятельной работы

в 6 классах

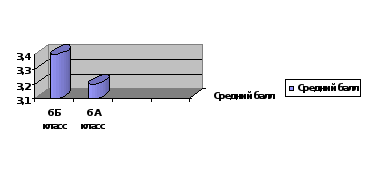
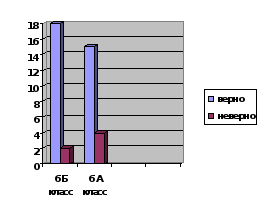
Диаграмма 1 Средний балл выполнения самостоятельной работы

в 6 классах

Классификация ошибок в работах учащихся 6 классов

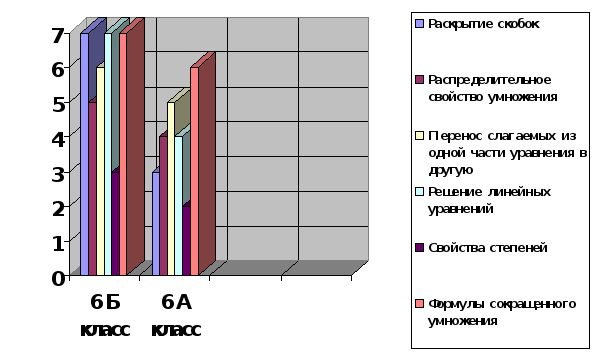Диаграмма 2 Классификация ошибок в работах учащихся 6 классов

Приложение 4

Анализ ошибок учащихся по математике

6 класс Выражения, тождества, уравнения

1.Ученики знают распределительное свойство умножения относительно сложения и вычитания.

Правило: а(b + с) = ab + ас а(b - с) = аb - ас.

Ошибки: - 2(а + 4) = -2а + 8; - 2(а - 4) = -2а - 8.

«Минус» и «плюс» в формулах сыграли плохую роль после того, как ученики познакомились с отрицательными числами. Надо быть внимательными.

2.Правила раскрытия скобок все знают, а при применении забывают и выполняют его только для первого слагаемого.

Правило: + (а -b + с) = а - b + с; -(а-b- с) = -а + b - с.

Ошибки: - (5a + b- х) =-5а+ b- х.

3.Правило переноса слагаемых из одной части уравнения в другую.

Правило: при переносе слагаемых из одной части уравнения в другую их знаки меняются на противоположные. 5х - 7 = 2x + 9;

Ошибки: 5х + 2x = 9 - 7.

4.Решение линейного уравнения. Привычка из начальной школы большее число делить на меньшее «заставляет» при решении уравнений учащихся совершать ошибку, а надо всего то знать правило нахождения неизвестного множителя или правило деления обеих частей уравнения на одно и то же, отличное от нуля число. Правило ах = b; (а не равно 0) х =  Ошибки: 6х =2; х = 3

5. Правило: при раскрытии скобок с применением распределительного свойства умножения нужно каждое слагаемое умножить на число.

2х - 5(х + 2) = 2х - 5х - 10;

Ошибки: 2х - 5(х + 2) = 2х - 5х +10.

Приложение 5

Анкета (Перед уроком – презентацией)

1. Укажите ваш возраст.
2. Укажите ваш пол.
3. Доводилось ли вам слышать подобную фразу: «Дважды два равно пяти» или хотя бы: «Два равно трем»?
4. Знакомо ли вам понятие «Софизм»?

(После урока – презентации)

1. Постарайся дать определение этого понятия самостоятельно.
2. Надо ли знакомить учащихся на уроках с софизмами?
3. Как ты думаешь, для чего нужны софизмы?
4. Хотел бы ты больше узнать о софизмах?
5. Как ты считаешь, какую роль для тебя может сыграть более глубокое знакомство с софизмами?

26