ДЕПАРТАМЕНТ СМОЛЕНСКОЙ ОБЛАСТИ
ПО ОБРАЗОВАНИЮ И НАУКЕ
Сафоновский филиал областного государственного бюджетного профессионального образовательного учреждения «Смоленская академия профессионального образования»
(Сафоновский филиал ОГБПОУ СмолАПО)
Исследовательская работа по теме
«Влияние модуля упругости материала, момента инерции его поперечного сечения на деформацию образца при статических испытаниях на изгиб»
Составитель: Савельева Людмила Николаевна
Сафоново 2017
Содержание
| № п/п | Название темы | Стр. |
| 1 | Введение | 3 |
| 2 | Методы исследования | 5 |
| 3 | Статические испытания на изгиб | 7 |
| 4 | Проведение оценки результатов испытания на изгиб | 19 |
| 5 | Заключение | 22 |
| 6 | Используемая литература | 24 |
Введение
Каждая деталь машины или инструмент должны обладать определёнными механическими свойствами (прочностью, пластичностью, упругостью и др.) От этих свойств зависит качество деталей, а также обрабатываемость металла. Чтобы убедиться, что деталь удовлетворяет тем требованиям, которые к ней предъявляются, производят механические испытания.
Стали и сплавы еще долгие годы останутся основным конструкционным материалом, применяемым в промышленности, на транспорте и в строительстве. В нашей стране, как известно, еще совсем недавно металла выплавлялось больше, чем в других странах, но используется он пока менее эффективно. Различные отрасли современной техники предъявляют высокие требования к надежности изделий, а следовательно, и к качеству металла, в частности к таким его свойствам, как прочность, упругость, выносливость, вязкость, пластичность, твердость.
Характеристики механических свойств являются основой инженерных расчетов на прочность и надежность деталей машин и сооружений, а также широко используется для оценки качества и выявления роли изменения технологии металлургического производства на качество металлоконструкции. При выборе метода механических испытаний металлов встречаются и иногда приходят в противоречие несколько условий. Главным из них является желание по возможности полнее имитировать служебные условия работы металла в изделии. Но это ограничивается аппаратурой, применяемой для выполнения испытаний, способом изготовления и формой образцов и далеко не всегда можно точно воспроизвести служебные условия нагружения металла. Условие создания новой техники требует знание поведения металла при особых формах его нагружения и эксплуатации.
3
Среди этих особых форм нагружения следует отметить медленные периодические изменения нагрузки как с сохранением её знака, так и с переменным знаком в условиях ползучести, длительной прочности и усталости при силовых режимах нагружения.
В проблеме повышения долговечности машин металловедческие аспекты являются определяющими, ибо только оптимально выбранные качественные материалы в первую очередь способны продлить ресурс и эффективность работы
машин и конструкций.
На ряде примеров показано, что вновь разрабатываемые методы определения характеристик являются развитием и совершенствованием существующих стандартных методов испытаний. В этом проявляется взаимосвязь и преемственность существующих с вновь разработанными методами испытаний по определению характеристик механических свойств металлов. Знание этой связи даёт возможность обоснованно, с определённой степенью вероятности переходить от сложных механических испытаний к более простым.
Изучение механических свойств металлических материалов необходимо для обеспечения требуемого качества продукции. Вопрос качества продукции стал очень актуальным в настоящее время. Предприятия-изготовители занимаются постоянным изучением требований потребителей, для удовлетворения их потребностей и их предвосхищения. Проведение испытаний, имитирующих условия эксплуатации, с помощью современного оборудования позволяет с необходимой точностью определять механические свойства материалов. Результаты испытаний используются для дальнейшего применения в производстве, других испытаниях.
4
Цель работы:
1. Экспериментальная проверка линейности связи деформации и нагрузки в пределах упругости материала при плоском изгибе балки. Определение числовых значений упругих постоянных (модуля упругости Е), физического смысла этих постоянных, сравнение полученных значений с теоретическими значениями.
Для достижения поставленной цели необходимо решение следующих задач:
- теоретически и экспериментально исследовать взаимосвязь деформации образцов различного состава, а также структуры, и нагрузки в пределах упругости материала при плоском изгибе балки с целью обеспечения и обоснования единого подхода к изучению процесса поперечного изгиба;
- исследовать и получить значения упругих постоянных материалов (модуль упругости Е), характеризующих способность материала сопротивляться различным видам деформаций при воздействии на них внешних нагрузок;
- совершенствовать экспериментальную базу для исследования характеристик механических свойств в связи с развитием методов испытаний их автоматизацией, с применением программ для обработки экспериментальных данных.
5
Методы исследования
Работа выполнена с применением комплекса исследований, включающих аналитические и лабораторные испытания.
В процессе проведения работы использованы следующие методики: стандартные механические испытания образцов для определения механических характеристик различных сплавов на изгиб при статическом нагружении; статистическая обработка экспериментальных данных.
Объектами исследования были сплавы: AlMgSi0.5 F22 - алюминиевый
деформируемый сплав, 9 SMn 28 - автоматная сталь.
Образцы для испытания прямоугольного поперечного сечения размерами 40х12 мм, длиной 320 мм.
Компьютерная система записи данных измерений дала возможность записи данных измерений, программное обеспечение позволило выводить, на дисплей диаграммы, таблицы учетных записей, а так же редактирование и создание отчетов, сохранение и распечатывание полученной информации.
6
1 Статические испытания на изгиб
Испытание на изгиб обусловлено широкой распространенностью этой схемы нагружения в реальных условиях эксплуатации и большей ее мягкостью по сравнению с растяжением, что дает возможность оценивать свойства материалов, хрупко разрушающихся при растяжении. Испытания на изгиб удобны для оценки температур перехода из хрупкого состояния
в пластичное.
Испытания проводились на универсальной установке для статических испытаний материалов WP300. Конструкция установки позволяет проводить спектр различных экспериментов, требующих наличия растягивающих или сжимающих усилий. Компактные размеры установки и небольшой вес делают ее мобильной и позволяют устанавливать на обыкновенных столах.
При испытаниях на изгиб применялась схема нагружения образца, лежащего на неподвижных опорах: нагрузка прикладывалась сосредоточенной силой на середине расстояния между опорами, расстояние между опорами изменялось от 300мм до 100 мм.

Рис.1- Образец стальной балки на опорах
7

Рис.2а) Студенты проводят исследовательскую работу


Рис.2 б) - Испытание образцов на изгиб
8
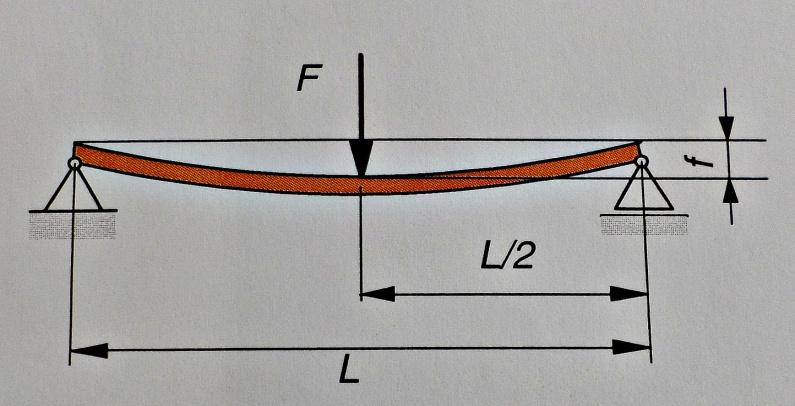
а)

в)

с)
Рис.3 - а) схема нагружения образца; в)- эпюра поперечных сил;
с)- эпюра изгибающего момента
9


Рис.4 – Поперечное сечение образцов прямоугольного типа
Деформация плоского поперечного изгиба вызывается силами, лежащими в плоскости симметрии поперечного сечения балки и направленными перпендикулярно к ее оси. Ось балки располагается в плоскости действия нагрузки.
При изгибе в широких образцах (с отношением ширины к высоте сечения более трех) создается двухосное напряженное состояние из-за затруднения поперечной деформации. Нижняя часть образца оказывается растянутой, верхняя — сжатой. К тому же напряжения, связанные с величиной изгибающего момента, различны по длине и сечению образца.
Максимальные напряжения возникают вблизи поверхности. Все это затрудняет оценку средних истинных напряжений и деформаций, строго характеризующих механические свойства при изгибе.
При изгибе сосредоточенной силой помимо изгибающих моментов, вызывающих нормальные напряжения, возникают перерезывающие силы Q и соответствующие им касательные напряжения, которые действуют попарно в сечениях, параллельных и перпендикулярных оси образца.
Касательные напряжения достигают максимума в центре образца, где нормальные равны нулю.
10
Касательные напряжения могут оказать существенное влияние на прочность и жесткость при изгибе лишь в случае короткого образца, в нашем случае эти напряжения меньше нормальных напряжений.
Отличительной особенностью испытаний на изгиб, является неравномерное распределение напряжений по сечению образца. Вследствие этого при изгибе, различают два вида предела текучести: номинальный, рассчитываемый по формулам упругого изгиба в предположении линейного распределения напряжений по сечению вплоть до достижения крайними растянутыми волокнами заданного допуска на остаточное удлинение при определении предела текучести, и реальный, учитывающий действительное распределение напряжений по сечению образца при изгибе и определяемы как истинное напряжение, при котором в крайних волокнах образца возникает остаточная деформация, равная по величине заданному условному допуску. Обычно при определении пределов текучести при изгибе, также, как и при растяжении, принимается допуск на остаточное удлинение, равный 0,2%.
Номинальный предел текучести при изгибе, значение которого используется в инженерных расчетах, для большинства металлических материалов приблизительно на 20% превосходит предел текучести при растяжении.
Реальный предел текучести, используемый обычно в исследовательских целях, например, для' сопоставления сопротивления малым упруго-пластическим деформациям при разных видах нагружения, рек9мендуется определять при испытании прямоугольного образца графически по диа- грамме «наибольшее нормальное напряжение — наибольший сдвиг», полученной последовательным пересчетом из диаграмм «изгибающее усилие — прогиб» и «изгибающий момент — удлинение».
11
Перед испытанием вычисляют наибольшую величину нагрузки, которая может быть приложена к балке, не вызывая напряжений больше допускаемых.

Рис.5 – Поперечное сечение образцов прямоугольного типа
Проведем исследования образца с поперечным сечением - рис. 5
F max = (2 σ max x B x H) / 3L, где (1)
F max – максимальная величина нагрузки;
σ max - максимальное нормальное напряжение;
В, Н – размеры поперечного сечения образца;
L – длина
Максимальное нормальное напряжение для стального образца 380 Н/ мм2
Максимальное нормальное напряжение для алюминиевого образца
110 Н/ мм2
F max = (2 х 380 х 40 х 122 / 3х300 = 4,66Н;
F max = (2 х 110 х 40 х 122 / 3х300 = 1,4Н
Образцы, как видно, явно не перегружены.
Таблица 1 - Допускаемые нагрузки для каждого образца
| Материал | 9SMn28 | AlMgSi0.5F22 |
| F max ; Н/ мм2 | 4,7 кН | 1,4кН |
12
Таблица 2 - Экспериментальные значения прогиба стального и алюминиевого образца при длине пролета 100, 200 и 300 мм
| 9SMn28 | F max = 4,7 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,4 | 0,70 | 3,00 |
| AlMgSi0.5F22 | F max = 1,4 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,25 | 0,85 | 2,05 |
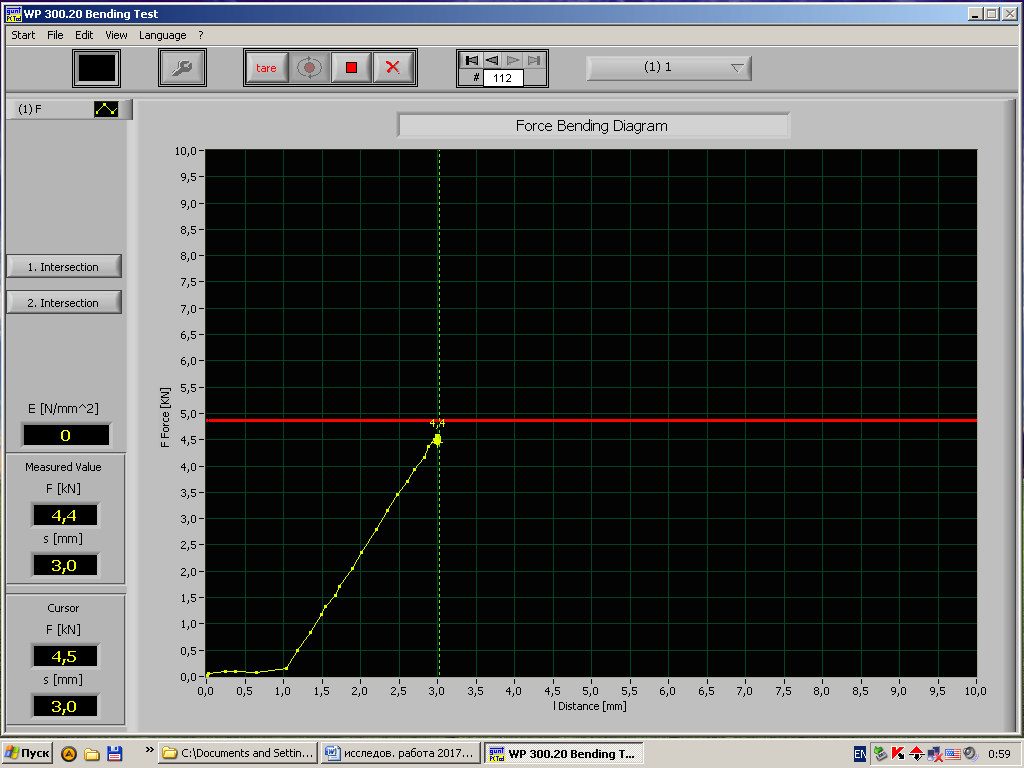
Рис.6 - Диаграмма «нагрузка – деформация» стального образца при длине пролета 300мм
13
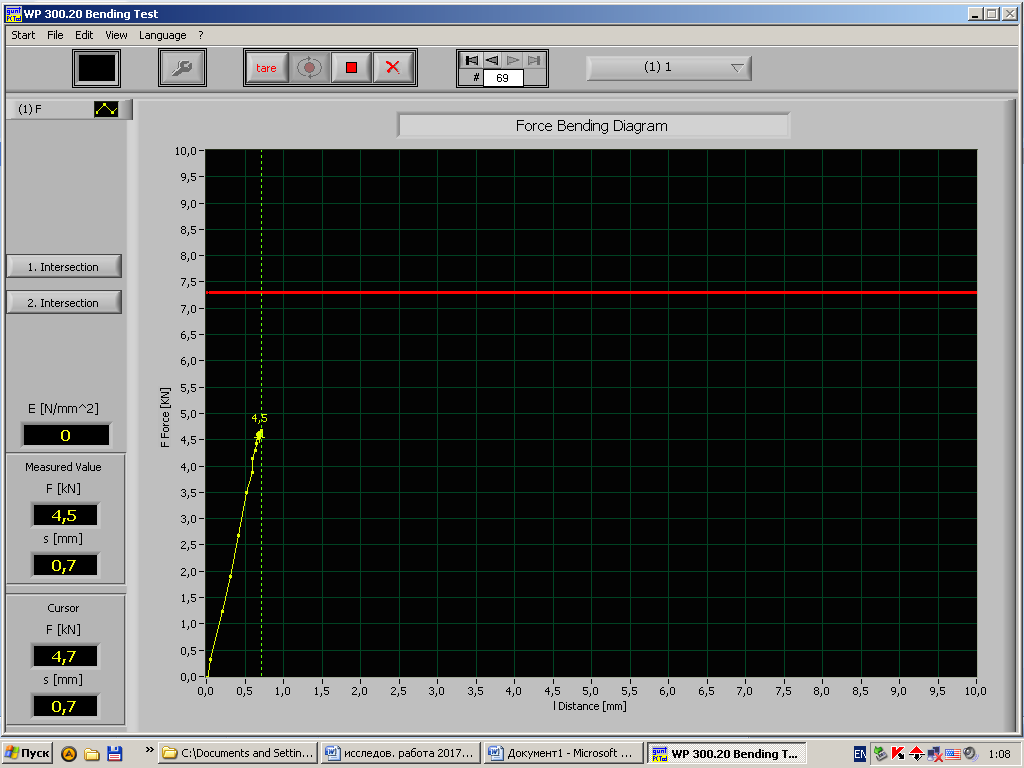
Рис.7- Диаграмма «нагрузка – деформация» стального образца при длине пролета 200мм
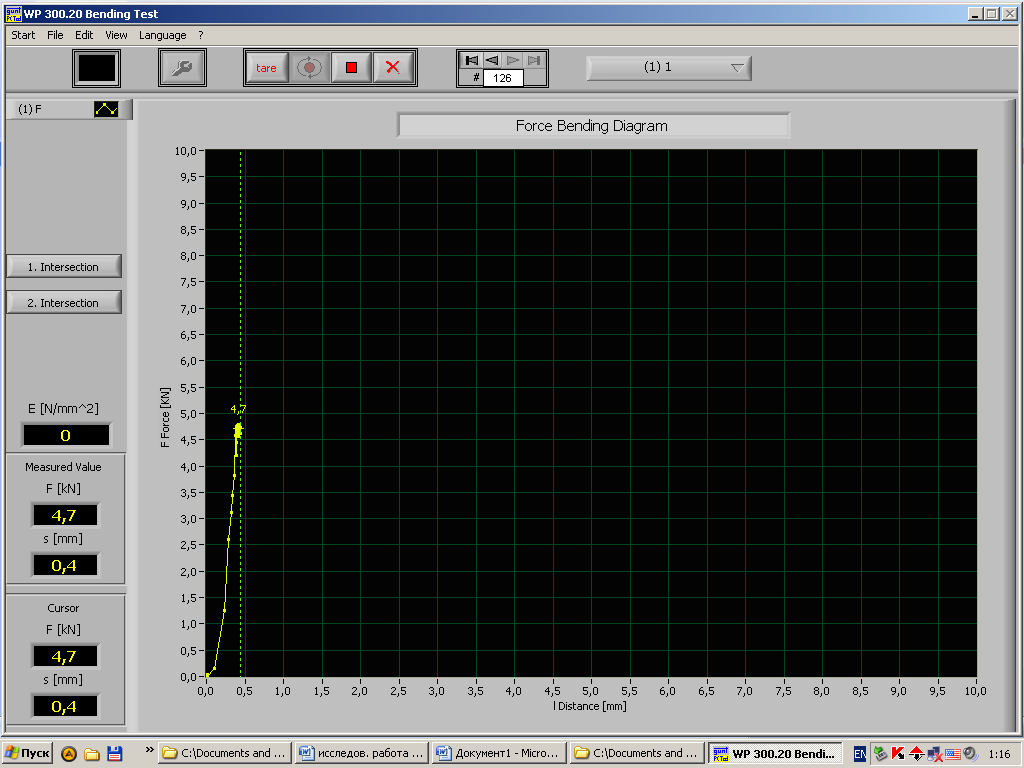
Рис.8- Диаграмма «нагрузка – деформация» стального образца при длине пролета 100мм
14
Прогиб образца определяется по формуле:
f = (F x L3) / 48 E x I, где (2)
f – прогиб образца;
F – максимальная нагрузка;
L – длина пролета;
E – модуль упругости материала;
I –осевой момент инерции
Момент инерции прямоугольного сечения образца с размерами
В =40мм, Н = 12мм:
I = (B x H3) / 12 = 40 х 123 / 12 = 5760 мм4
Тогда прогибы расчетные для стального образца равны:
f = 4700 х 3003 / 48 х 210000 х 5760 = 2,19 мм
f = 4700 х 2003 / 48 х 210000 х 5760 = 0,65 мм
f = 4700 х 1003 / 48 х 210000 х 5760 = 0,08 мм
Прогибы расчетные для алюминиевого образца равны:
f = 1400 х 3003 / 48 х 210000 х 5760 = 1,98 мм
f = 1400 х 2003 / 48 х 210000 х 5760 = 0,59 мм
f = 1400 х 1003 / 48 х 210000 х 5760 = 0,07 мм
Модуль упругости определяется по формуле:
E = (F x L3 ) / (4f x B x H3), где (3)
E – модуль упругости материала;
F – максимальная нагрузка;
L – длина пролета;
f – прогиб образца;
В,Н – размеры поперечного сечения образца
15
Тогда для стального образца:
E – (4700 x 3003) / (4x 3,00 х 40 х 123) = = 193,700 Н/мм2
E – (4700 x 2003) / (4x 0,7 х 40 х 123) = = 172,100 Н/мм2
E – (4700 x 1003) / (4x 0,4 х 40 х 123) = = 73,900 Н/мм2
Таблица 4 - Полученные экспериментальные данные стального образца, которые противопоставляются расчетным
| 9SMn28 | F max = 4,7 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,40 | 0,70 | 3,00 |
| fрасч., мм | 0,08 | 0,65 | 2,19 |
| Е, Н/мм2 | 73,900 | 172,100 | 193,700 |
Для алюминиевого образца:
E – (1400 x 3003) / (4x 2,05 х 40 х 123) = = 66,700 Н/мм2
E – (1400 x 2003) / (4x 0,85 х 40 х 123) = = 47,700 Н/мм2
E – (1400 x 1003) / (4x 0,25 х 40 х 123) = = 20,300 Н/мм2
Таблица 5 - Полученные экспериментальные данные алюминиевого образца, которые противопоставляются расчетным
| AlMgSi0.5F22 | F max = 1,4 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,25 | 0,85 | 2,05 |
| fрасч., мм | 0,07 | 0,59 | 1,98 |
| Е, Н/мм2 | 20,300 | 47,700 | 66,700 |
Таблица 6 - противопоставления модуля упругости материала расчетного и представленного в справочной литературе (для пролета длиной 300 мм).
| Материал | 9SMn28 | AlMgSi0.5F22 |
| Е, Н/мм2 | 193,700 | 66,700 |
| Е справ., Н/мм2 | 210,000 | 69,000 |
16

Рис.9 – Поперечное сечение образцов прямоугольного типа
Проведем исследования образца с поперечным сечением - рис. 9
Таблица 7 - Значения прогибов образцов из различных материалов для прямоугольного сечения – рис.9
| f, мм |
| L, мм | 100 | 200 | 300 |
| 9SMn28; F max =4,7 кН | 0,2 | 0,2 | 0,4 |
| AlMgSi0.5F22; F max =1,4 кН | 0,02 | 0,06 | 0,19 |
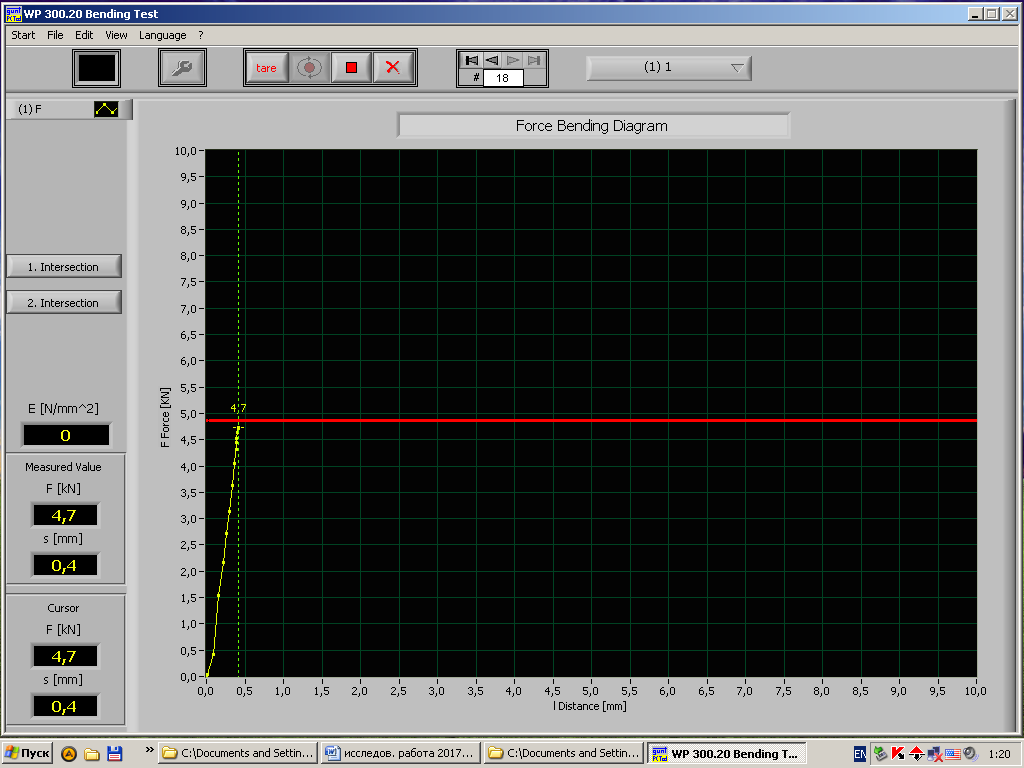
Рис.10 - Диаграмма «нагрузка – деформация» стального образца при длине пролета 300мм
17
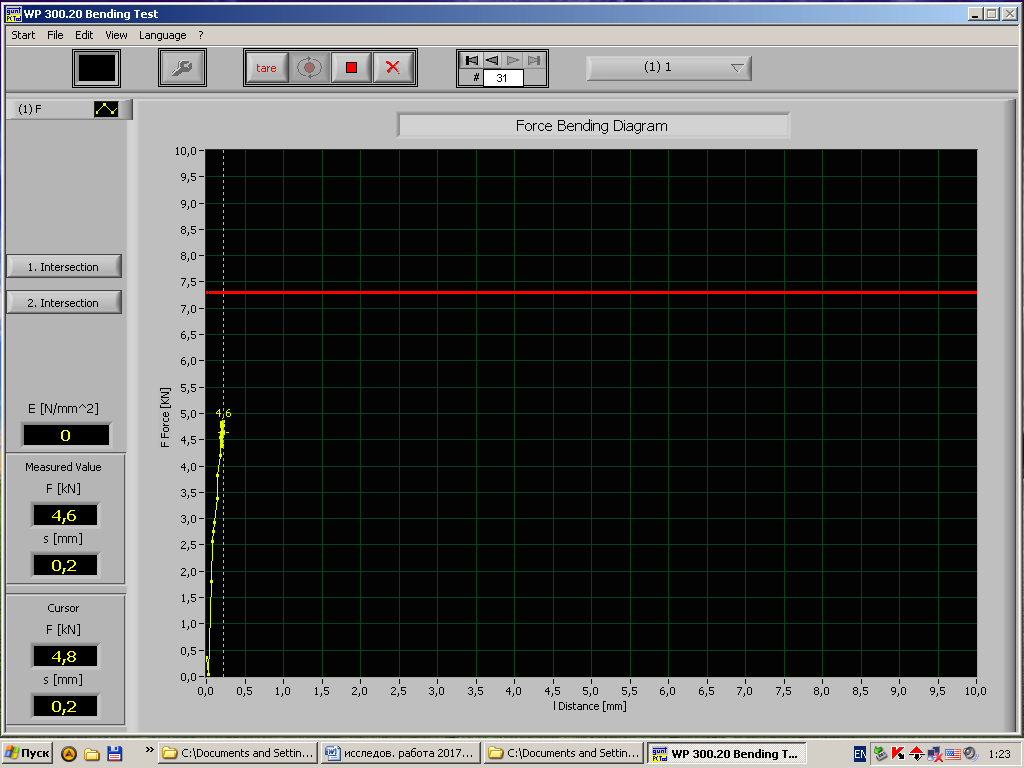
Рис.11 - Диаграмма «нагрузка – деформация» стального образца при длине пролета 200мм
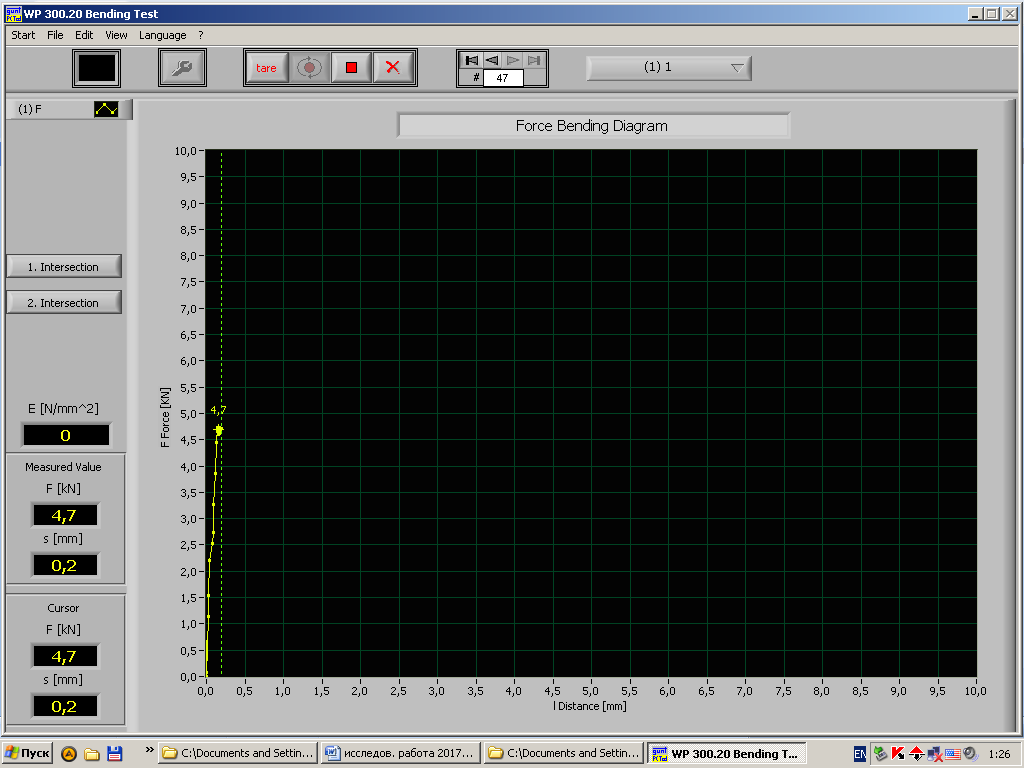
Рис.12 - Диаграмма «нагрузка – деформация» стального образца при длине пролета 100
18
Определим момент инерции, величину прогиба образца с поперечным сечением на рис.9 по известным формулам:
I = (B x H3) / 12 = 12 х 403 / 12 = 64000 мм4
f = (F x L3) / 48 E x I, где (4)
f - прогиб;
F - максимальная нагрузка;
L – длина пролета;
E – модуль упругости материала;
I – момент инерции сечения
Данные сводим в таблицу.
2 Обработка результатов испытаний.
Нагрузка и результирующий прогиб берутся непосредственно из диаграммы измерений испытания на изгиб с более жесткими образцами. Образец не может быть деформирован пластически и по возможности деформируется упруго. Полученные значения экспериментальным путем подвержены ошибкам. Ошибки, вызванные при использовании образца, расположенного вертикально, очень малы и могут быть вычислены путем вычитания вычисленных значений из фактически измеренных. Жесткость образца, расположенного в вертикальном положении в несколько раз выше, чем у образца, расположенного в плоскости, прогиб уменьшается, благодаря чему деформация самой системы в измеренном прогибе имеет более высокую пропорцию, поэтому может быть использована для коррекции всех значений отклонений, измеренных во время испытания на изгиб с одинаковой нагрузкой. Для этого каждый измеренный прогиб скорректирован с учетом формулы:
19
f откор. = f - fв (5)
f сткор - скорректированный прогиб;
f - прогиб, полученный экспериментально;
fв - деформация устройства
Ни одно устройство не является полностью неэластичным, однако оно должно оставаться в пределах диапазона упругости при допустимом использовании и не должно быть постоянно деформированным. Постоянная деформация возникает, как только устройство испытывает деформацию в пластическом диапазоне. Так как устройство рассчитано на нагрузку 20 кН, то деформация в области упругости не критична для правильной работы, но может исказить результаты измерений. Упругая деформация устройства проявляет себя как удлинение рамы при испытаниях на изгиб, а также при изгибе поперечины и двутавровой балки. Это удлинение добавляется к фактическому прогибу образца, следовательно, изгиб искажает измеренное отклонение. Из-за природы демонстрационного устройства, его упругая деформация сильнее, чем в промышленных испытательных машинах, и при изгибающей нагрузке определяется как отклонение устройства fв,, не линейно зависит от нагрузки, а точнее зависит от более высокой мощности нагрузки.
Таблица 8 – Значения упругой деформации устройства при испытании стальной балки (f, - fрасч. )
| 9SMn28 | F max = 4,7 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,2 | 0,2 | 0,4 |
| fрасч., мм | 0,01 | 0,06 | 0,20 |
| fв, мм | 0,19 | 0,14 | 0,2 |
20
Таблица 9 – Значения упругой деформации устройства при испытании алюминиевой балки (f, - fрасч. )
| AlMgSi0.5F22 | F max = 1,4 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,02 | 0,06 | 0,19 |
| fрасч., мм | 0,01 | 0,05 | 0,18 |
| fв, мм | 0,01 | 0,01 | 0,01 |
Таблица 10 – Значения скорректированного прогиба и модуля упругости
для стального образца
| 9SMn28 | F max = 4,7 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,40 | 0,70 | 3,00 |
| fв, мм | 0,19 | 0,14 | 0,2 |
| f кор, мм | 0,21 | 0,56 | 2,88 |
| Е кор, Н/мм2 | 121.400 | 200,000 | 209,600 |
Таблица 11 – Значения скорректированного прогиба и модуля упругости
для алюминиевого образца
| AlMgSi0.5F22 | F max = 1,4 кН |
| L, мм | 100 | 200 | 300 |
| f, мм | 0,25 | 0,85 | 2,05 |
| fв, мм | 0,01 | 0,01 | 0,01 |
| f кор, мм | 0,24 | 0,84 | 2,04 |
| Е кор, Н/мм2 | 21,100 | 48,200 | 67,000 |
Таблица 12 – Модуль упругости справочный и полученный экспериментальным путем при испытании образцов на изгиб
| Материал | 9SMn28 | AlMgSi0.5F22 |
| Е, Н/мм2 | 209,600 | 67,000 |
| Е справ., Н/мм2 | 210,000 | 69,000 |
Как видно из приведенных данных отклонения значений модуля упругости составляют около 3%.
21
Заключение
Данные исследования и обобщения полученных результатов позволили проверить правильность требований, заложенных в нормативные документы для' обеспечения сопоставимости и воспроизводимости экспериментальных результатов, получить важный в практическом отношении материал, который подчеркивает преемственность и взаимосвязь методов с уже существующими стандартными методами испытаний по определению характеристик механических свойств металлопродукции.
В связи с этим при рассмотрении и анализе полученных данных в исследовательской работе, особое внимание было уделено вопросам, обеспечивающим возможность получения сопоставимых результатов. Показано, что характеристики различаются по степени пластических деформаций в зонах, уровню номинальных напряжений, полученные результаты указывают на то, что определяемые по стандарту характеристики используются для сравнения различных вариантов химического состава, технологических процессов изготовления, обработки и контроля качества металлов и сплавов при металловедческих исследованиях. Такая классификация и систематизация экспериментальных данных необходима для накопления банка данных и их последующего статистического анализа.
Лабораторные исследования позволили приобрести практические навыки анализа результатов испытания материалов и определения основных показателей их механических свойств, изучить устройство и работу универсальной машины для испытания образцов материалов, проанализировать полученные данные свойств сплавов.
Полученные исследования могут быть использованы для суждения о сопротивлении материала, сопоставления материалов при обосновании их выбора для машин и конструкций; контроля качества материалов; оценки
22
долговечности элементов конструкций на основании данных об их напряженном состоянии.
Показано, что метод измерения деформации от нагрузки обусловлен не только простотой измерения, но и тем, что величина прогиба дает представления о комплексе механических свойств металла, определяемых другими видами испытаний, в частности, испытаниями на поперечный изгиб.
Результаты исследовательской работы войдут в практическое пособие для методических указаний к лабораторным работам, которые используются при чтении лекций по разделам дисциплины «Техническая механика», выполнении самостоятельных работ и лабораторного практикума.
23
СПИСОК ЛИТЕРАТУРЫ
1. Гудков А. А., Славский Ю. И. Методы измерения твердости металлов и сплавов. М., Металлургия, 1982, 168 с.
2. Гудков А. А., Славский Ю. И., СавилЬва Т. П. Стандартизация методов измерения твердости металлопродукции. Анализ отечественного и зарубежного опыта. М., Изд. стандартов, 1985, 56 с
3. Гудков А. X., Бирун Н. А., Минашин А. В., Чеботарев В. И. Новые стандарты на методы измерения твердости // М., Стандарты и качество, 1979, №11, стр. 22-24.
4. Гудков А. А., Минашин А. В., Пирусский М. В. Развитие методов определения вязкости разрушения низколегированных сталей при статическом нагружении. // Тез. докл. Всесоюзного симпозиума по механике разрушения (Киев, 24 - 26 сентября 1978 г.). Киев, ИПП АН УССР, 1
5. Гудков А. А., Курчанова Е. А., Минашин А. В. ГОСТ 9651-73. Металлы. Методы испытаний на растяжение при повышенных температурах // Экспресс-стандарт. Качество. Стандарты. Метрология (Госстандарт СССР ВНИИКИ). М., 1973, вып. 51, с. 2-3.
6. Качалов J1. М. Основы механики разрушения. — М. : Наука, 1974. - 312 с.
7.Морозов Е. М., Никишов Г. П. Метод конечных элементов в механике разрушения.— М.: Наука, 1980. — 254 с.
8. Партой В. 3. Морозов Е. М. Механика упруго-пластического разрушения. М.: Наука, 1974. — 416 с.
9.Тимошук Л. Т. Механические испытания металлов. — М.: Металлургия, 1971. — 224 с.
10. Тимошук Л. Т., Гудков А. А., Зотеев В. С. Поведение материалов при ползучести в нестационарных условиях // Специальные стали и сплавы. Сб. трудов ЦНИИЧМ. М„ Металлургия, 1967, вып. 52, с. 157-159.
11. Фридман Я. Б. Механические свойства металлов. Изд. 3-е,-переработанное и дополненное. В двух частях. Часть первая. Деформация и разрушение, — М.: Машиностроение, 1974, — 472 с.
12.Фридман Я. Б. Механические свойства металлов. Изд.'3-е, переработанное и дополненное. В двух частях. Часть вторая. Механические испытания. Конструкционная прочность. — М.: Машиностроение, 1974. — 368 с.
13. Черпанов Г. П. Механика хрупкого разрушения. — М.: Наука, 1974. — 640с.
24
































