Государственное автономное профессиональное
образовательное учреждение
«Казанский нефтехимический колледж имени В.П. Лушникова»
Исследовательская работа
Финансовая грамотность и математика
Выполнили: Курочкина Ангелина Ренатовна,
Ахмадуллина Чулпан Завдатовна,
II курс
Руководитель: Маркина Людмила Андреевна
Казань, 2023
Оглавление
| Введение | 3 |
| Цели и задачи исследования | 4 |
| Основная часть | 5 |
| Заключение | 15 |
| Библиографический список | 16 |
Введение
В колледже учатся ребята 16-17 лет и старше, многие из них приезжие, живут самостоятельно, отдельно от родителей, на старших курсах большинство студентов работают.
Поэтому вопросы как распоряжаться собственными деньгами, как планировать личный бюджет, принимать осознанные решения при планировании покупок, как умело пользоваться заемными средствами, как накопить средства, как оценить риски вложений, для нас очень актуальны.
Финансовая грамотность студентов формируется на основе всего комплекса предметов учебного плана. Это и обществознание, и экономика, экономика организации, менеджмент, и, конечно же, математика. Без математических расчетов, без умения читать графики и диаграммы даже в повседневной жизни никак не обойтись. Нас заинтересовал вопрос, как связаны математические дисциплины и курс финансовой грамотности, какие финансовые задачи можно рассматривать в рамках математических дисциплин.
Цель исследования:
показать связь финансовой грамотности и математических наук, мотивировать себя и других студентов к занятиям математикой через формирование умения применять математические знания при управлении личными финансами, учете доходов и расходов, решении экономических вопросов и задач.
Задача исследования:
Изучив содержание учебного материала дисциплин, связать элементы финансовой грамотности и элементы математических дисциплин, составить банк интересных задач.
Основная часть
На начальном этапе нами были проанализированы темы таких математических дисциплин, как Математика (общеобразовательный цикл), Математика (естественнонаучный цикл), Элементы высшей математики.
Также была рассмотрена тематика учебников:
Алимов Ш.А. и др. Математика: Алгебра и начала математического анализа, геометрия. 10-11 классы.
Мордкович А.Г. Алгебра и начала анализа. 10 класс для общеобразовательных учреждений (профильный уровень) части 1и 2
Башмаков М.И. Математика: учеб. для студентов учреждений сред. проф. образования.
Башмаков М.И. Математика: сборник задач профильной направленности: учеб. для студ. учреждений сред. проф. образования.
Кремер Н.Ш. Линейная алгебра: учебник и практикум
Жданова А.О., Савицкая Е.В. Финансовая грамотность: материалы для обучающихся
Вопрос стоял, в какие темы можно включить задачи, способствующие развитию финансовой грамотности у студентов.
Первая тема – Действительные числа.
Какие задачи мы можем решать в этом разделе? Конечно же, расчетные задачи на выбор оптимального варианта и задачи на проценты! Причем по своей тематике это могут быть абсолютно разные задачи.
Задачи на альтернативную стоимость.
Альтернативная стоимость — это ценность лучшего из отброшенных вариантов, при этом стоимость выбранного варианта — наименьшая из возможных.
1. Михаил хочет взять в аренду на 7 дней небольшой внедорожник для поездки в горы протяжённостью 3500 км. В прокатной компании есть две подходящих машины. Укажите внедорожник с наименьшей полной стоимостью аренды, исходя из данных, указанных в таблице. В ответе укажите полную стоимость аренды этой машины в рублях.
| Характеристики | Внедорожник А | Внедорожник В |
| Стоимость аренды | 4400 руб. в сутки | 4800 руб. в сутки |
| Расход бензина на 100 км пути | 14 литров | 12 литров |
| Используемый бензин и его стоимость | АИ-95 по цене 49 рублей за литр |
Решение:
Стоимость аренды на 7 дней можно вычислить по формуле:
C = (3500\100)*r*p+7*a
где r – расход в литрах на 100 км; p – цена за 1 литр бензина; a – стоимость суточной аренды.
Вычислим стоимость для внедорожников А и В:
Для внедорожника А: С=35*14*49+7*4400=54 810 руб.
Для внедорожника В: С = 35*12*49+7*4800 = 54 180 руб.
Дешевле получается аренда внедорожника В.
2. Иван Васильевич живет в деревенском доме постройки 1960-х годов и использует газ для отопления дома в холодное время года (6 месяцев в году). Расход газа в среднем составляет 700 куб. м в месяц, а стоимость 1 куб. м газа – 6,3 рубля. Иван Васильевич считает, что из-за износа дом теряет много тепла, и хочет сократить потери. Строительная фирма предложила хозяину утеплить дом пеноизолом, обещая снижение расхода газа на 30%. Общая стоимость работ и утеплителя составит 36 000 рублей. Если удастся достичь обещанной экономии газа, через сколько лет должно окупиться утепление дома? Ответ округлите до целого значения.
Решение:
Сначала найдем расход газа за 1 месяц:
700 куб.м. * 6.3 руб. = 4 410 руб.
Найдем экономию: Если 4 410 руб. = 100 %, то
30% = 4 410/100*30= 1323 руб.
4 410-1323=3087 руб.
Найдем через какое время окупятся 36 000 руб:
36 000:1323:6= 4.5…. Округляем, и ответ будет 5 лет
Задачи на личный бюджет, расходы и доходы.
Бюджет семьи — это план доходов, расходов и накоплений, описывающий возможности всех членов семьи в определённый период времени. Семейный бюджет необходим для удовлетворения основных потребностей всех членов семьи, которое невозможно без грамотных трат и разумной экономии.
Потребности человека безграничны. Для их удовлетворения нужны ресурсы, деньги. Чтобы грамотно распределить деньги, нужны знания в сфере финансов.
3. Летом килограмм клубники стоит 130 рублей. Маша купила 1 кг 200 г клубники. Сколько рублей сдачи она получит с 500 рублей?
Решение: Найдем стоимость покупки:
1 кг 200 г клубники стоит 1,2 · 130 = 156 рублей.
Значит, с 500 рублей Маша получит сдачи 500 − 156 = 344 рубля.
4. Сколько надо заплатить, если квартплата 7000 рублей просрочена, пеня равна 0,5% за каждый день просрочки, а оплата производится с задержкой на 30 дней?
Решение: 7000:100*0,5*30 = 1050 рублей
7000 + 1050 = 8050 рублей.
5. По тарифному плану «Просто как день» компания сотовой связи каждый вечер снимает со счёта абонента 18 руб. Если на счету осталось меньше 18 руб., то на следующее утро номер блокируют до пополнения счёта. Сегодня утром у Лизы на счету было 800 руб. Сколько дней (включая сегодняшний) она сможет пользоваться телефоном, не пополняя счёт?
Решение:
800/18 = 44,4, но так как 40% от 18 рублей (т. е. 7 рублей 20 копеек) не хватит, чтобы оплатить день общения — делаем вывод, что Лизе этих денег хватит на 44 дня.
6. Мама дает Леше 1500 рублей в неделю на проезд и карманные расходы. На проезд Леша тратит 20% полученных от мамы денег. Со следующего месяца проезд в транспорте подорожает на 30%. Сколько денег мама должна добавить Леше, чтобы его карманные расходы остались такими же, как до повышения цен на транспорт?
Решение:
Найдем, сколько денег Леша тратит на дорогу:
1500-100%
1% = 1500:100= 15 руб.
20%= 15*20=300 руб. Леша тратит на дорогу.
Теперь найдём на сколько рублей подрожал проезд:
300:100%= 3 руб.
30%*3=90 руб.
Значит, мама должна добавить 90 руб. на карманные расходы.
Задачи на доходы и налоги
Доход - денежные средства или материальные ценности, полученные государством, физическим или юридическим лицом в результате какой-либо деятельности за определённый период времени.
Налоги - это обязательные платежи, которые налогоплательщики обязаны перечислять государству, региону или муниципальному образованию при наступлении определенного события.
Подоходный налог - это налог, который россияне уплачивают из своих доходов. Основная ставка такого налога - 13 процентов. Правильнее такой налог называется "налог на доходы физических лиц" или сокращенно "НДФЛ".
7. Сумма подоходного налога составляет 13% от заработной платы начисленной работнику. Какой доход работник получит на руки, если сумма подоходного налога составила 7 007 рублей?
Решение:
Так как подоходный налог равен 13 % (7 007 руб.), то можно вычислить доход с вычтенным налогом:
100% - 13% = 87%
13% = 7 007 руб.
87% = х руб.
х = (7 007\13)*87= 46 893 руб.
8. Приятели Алексей и Борис сравнивают свои заработные платы. Алексей говорит, что его оклад по трудовому договору составляет 24 000 рублей в месяц, а Борис ежемесячно получает на карточку по 21 000 рублей. Ставка налога на доходы физических лиц равна 13%. Кто из приятелей зарабатывает больше? Какой оклад указан в трудовом договоре у Бориса?
Решение:
1) 24000-24000*0,13 = 20880 рублей получает Алексей на руки после вычета НДФЛ
2) 21000/0,87 = 24137,93 рублей –оклад Бориса.
Задачи на сбережения и инвестиции.
Банковский вклад (депозит) – сумма денег, размещенная в банке на специальном личном счете клиента. Вкладчик отдает банку свои деньги, и банк может ими пользоваться, пока клиент не захочет их забрать обратно, поэтому вклад можно понимать как долг банка перед клиентом. Обычно вклад делается на определенный срок (срочный) или до востребования (бессрочный), а за время, пока деньги находятся в распоряжении банка, он выплачивает вкладчику проценты.
Разумное финансовое поведение предполагает, что человек делает сбережения, то есть откладывает часть своих денег на будущее. Люди сберегают деньги с разными целями: накопить средства для крупной покупки, иметь запас на «черный день», использовать накопления как источник дополнительных доходов.
9. 1 января Виктор положил на банковский депозит 500 000 рублей под 11,5% годовых. Срок депозита – один год. Выплата процентов происходит в конце срока вместе с возвратом депозита. Через год Виктор хотел купить автомобиль стоимостью 690 000 рублей, получив депозит с процентами и добавив недостающую для покупки сумму. Какую сумму для покупки автомобиля должен добавить Виктор после возврата депозита?
Решение:
За 1 год проценты по вкладу: 500 000 * 11,5%= 57 500 руб.
В конце года возврат суммы с процентами: 500 000 +57500=557 500 руб.
Теперь найдем недостающую сумму: 690 000-557 500= 132 500 руб.
Мы заинтересовались вопросом, где в геометрии можно включить материал финансовой дисциплины? И нашли такую тему. При изучении многогранников можно поговорить о финансовой пирамиде, почему этот вид мошенничества носит такое название.
Следующие темы, которые нас заинтересовали – Показательная функция и Логарифмы. Мы уже говорили о проценте по вкладу. Но, что, если требуется найти сумму вклада через определенное количество лет, причем проценты капитализируются, то есть начисляются «проценты на проценты». Конечно, можно просчитать каждый год, но это очень долго. На помощь нам приходит показательная функция.
Задача:
Сколько денег получит вкладчик через 5 лет, если он положил на депозит с годовой капитализацией процентов 50000 рублей под 10% годовых.
Решение:
50000·1,15 = 80525,50 рублей
В этом случае говорят о сложных процентах и используют формулу
SN = (1 + 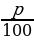 )N S, которая выражает функциональную зависимость вида y=ax.
)N S, которая выражает функциональную зависимость вида y=ax.
Обратная задача:
На счёт в банке положили 1 млн. рублей под 23% годовых. Через какое время сумма на счёте увеличиться в 2 раза?
Решение: Используя формулу сложных процентов, запишем:
2000000 = (1 + 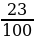 )N 1000000
)N 1000000
1,23N = 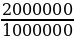
1,23N = 2
Требуется найти N. Зная понятие логарифма, это можно сделать довольно быстро.
N = log1,23 2 = 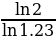 =
= 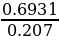 = 3.35.
= 3.35.
Еще одна интересная, на наш взгляд, тема курса математики – это Производная, её применение к исследованию функций. Здесь, конечно, задачи производственные. Но, мы - студенты колледжа, в дальнейшем можем стать предпринимателями, например. И разбор таких задач тоже представляет интерес.
Экономический смысл производной заключается в следующем: значение производной функции в данной точке есть предельные издержки производства при данном его объёме.
Задача 1:
Предположим, что функция затрат при производстве продукции имеет вид:
К(Х)=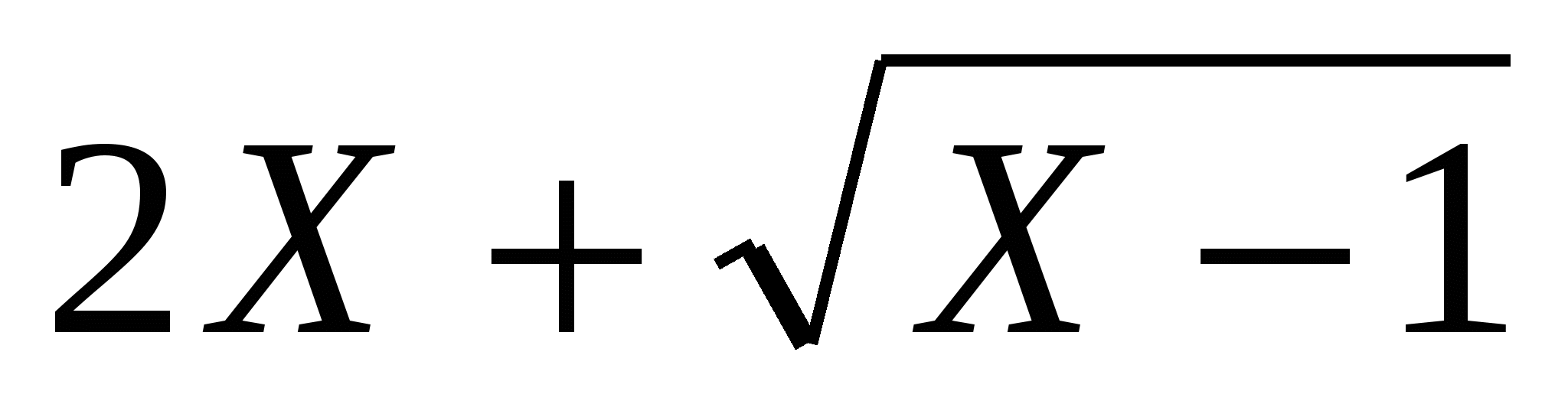 . Определить предельные издержки производства при увеличении объёма выпуска на 2 ед. и на 10 ед.
. Определить предельные издержки производства при увеличении объёма выпуска на 2 ед. и на 10 ед.
Решение:
Предельные издержки это рост затрат при увеличении объёма производства на 2 ед. и на 10 ед.
Математически, предельные издержки - это значение производной функции в точке.
Находим производную по правилам и формулам дифференцирования
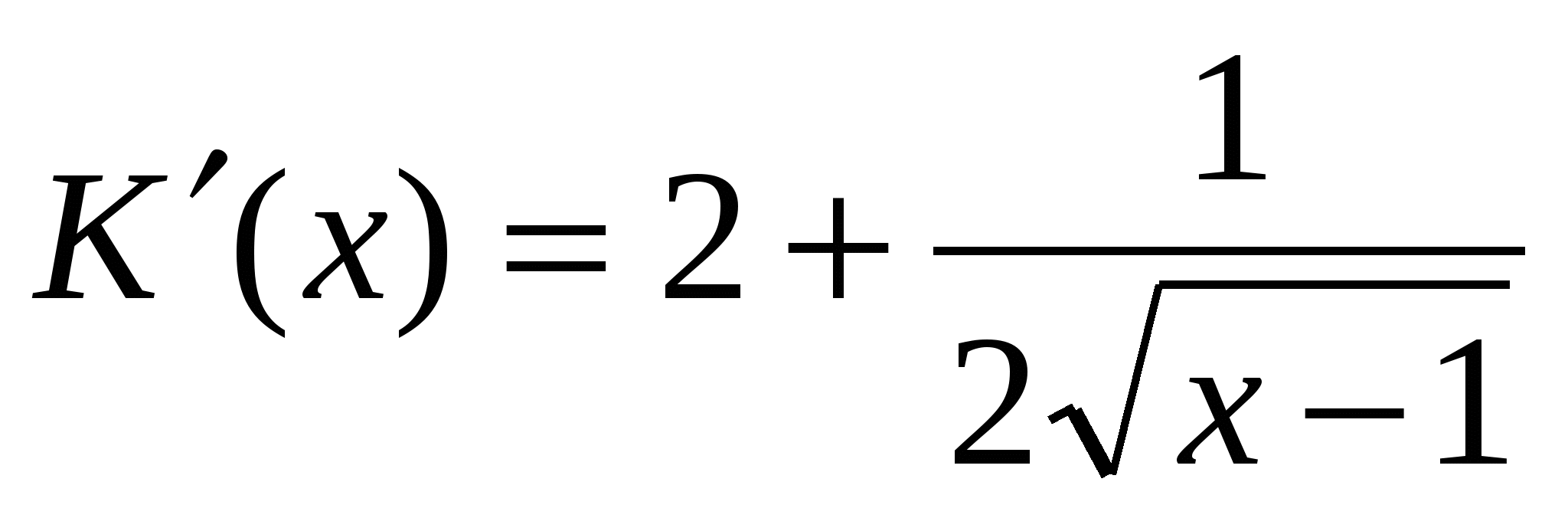
Считаем значение производной в точке 2 и в точке 10
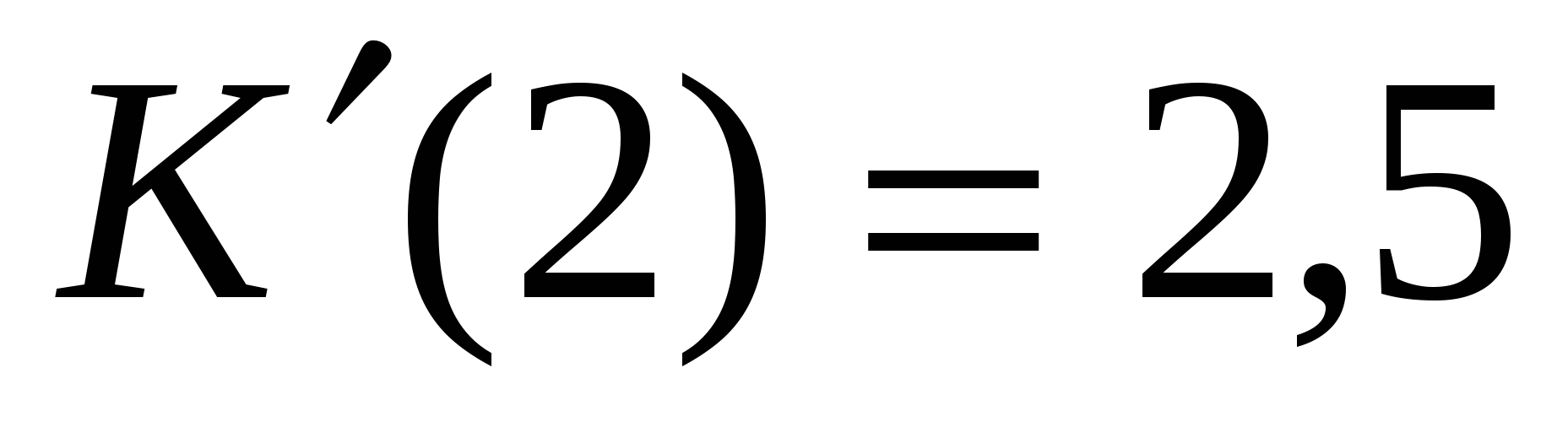
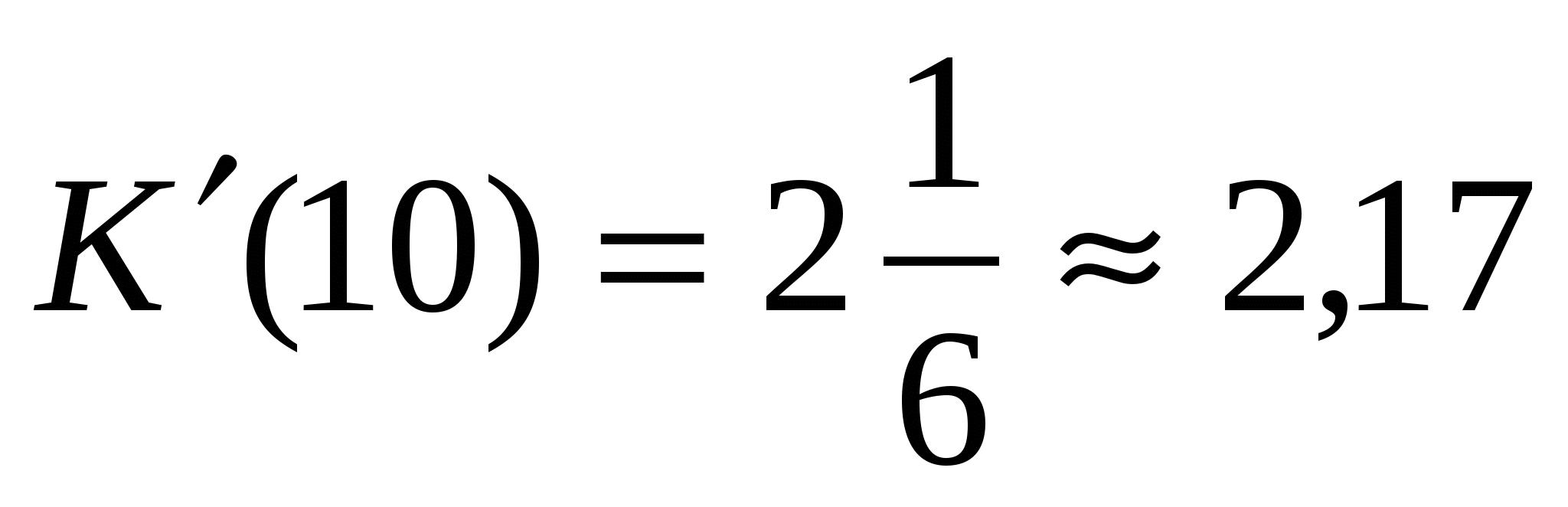
Таким образом, предельные издержки производства составляют 2,5 ден.ед. при росте объёма производства на 2 ед. и 2,17 ден.ед. при росте объёма производства на 10 ед.
Задача 2:
Предприятие производит Х единиц продукции.
Установлено, что зависимость финансовых накоплений от объёма выпуска задаётся формулой: 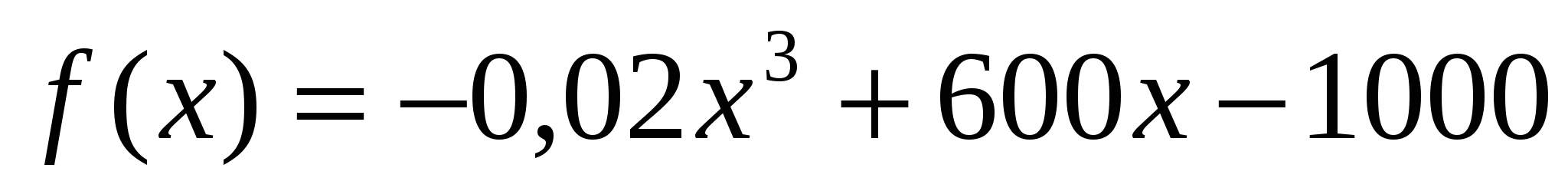 .
.
Определить максимально возможную величину финансовых накоплений.
Задача сводится к нахождению наибольшее и наименьшее значение функции.
Решение:
Находим производную
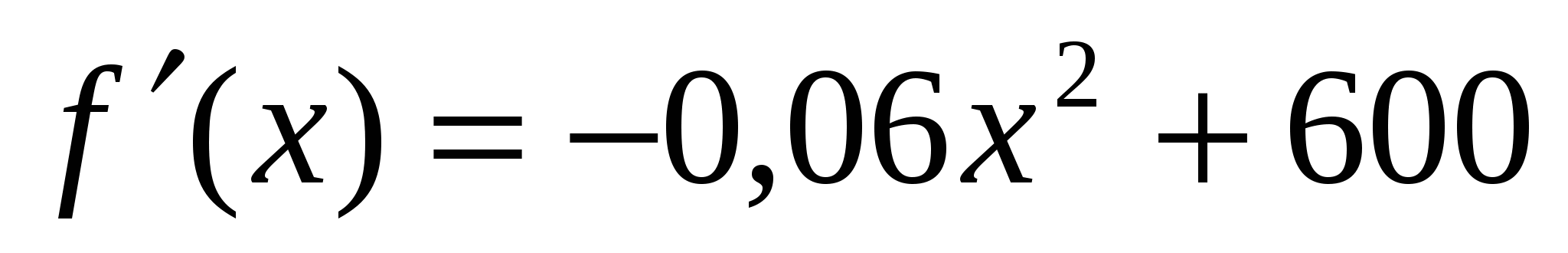
Приравниваем её к нулю, находим критические точки
- 0,06 x2 + 600 = 0
x1 = 100
x2 = -100
Чертим луч, отмечаем указанные точки на луче, расставляем знаки производной.
При переходе через точку 100 производная меняет знак с + на - .Значит, x=100 точка максимума, в ней и будет достигаться наибольшее значение функции.
Находим значение функции в этой точке
f(100) = 39000
Таким образом, финансовые накопления предприятия вырастут при увеличении объёма производства до100 единиц и достигнут суммы 39000 ден. единиц.
При изучении матриц мы снова обратили внимание на задачи с экономическим содержанием. С помощью матриц можно более компактно изображать экономическую информацию, а, используя методы решения систем линейных алгебраических уравнений, быстро находить ответы на поставленные вопросы.
Задача:
Предприятие производит следующие изделия: перчатки, сумки и портмоне. Для производства используется сырье 3-х видов. Известен расход сырья на единицу изделия и объем расхода сырья на 1 неделю (заданы в таблице). Необходимо найти еженедельный объем выпускаемой продукции каждого вида.
|
| перчатки | сумки | портмоне | Расход на 1 неделю |
| Сырье 1 | 6 | 2 | 0 | 280 |
| Сырье 2 | 1 | 0 | 1 | 60 |
| Сырье 3 | 3 | 2 | 4 | 310 |
Составим математическую модель задачи. Пусть x – это объем производства перчаток, y – объем производства сумок и z - объем производства портмоне. С учетом нормы расходы каждого вида сырья на единицу изделия составим систему уравнений:
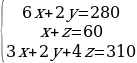
Решим данную систему по правилу Крамера
∆ = 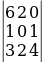 = 6·0·4 + 2·1·3 + 0·1·2 - 0·0·3 - 6·1·2 - 2·1·4 = 0 + 6 + 0 - 0 - 12 - 8 = -14
= 6·0·4 + 2·1·3 + 0·1·2 - 0·0·3 - 6·1·2 - 2·1·4 = 0 + 6 + 0 - 0 - 12 - 8 = -14
∆1 = 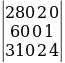 = 280·0·4 + 2·1·310 + 0·60·2 - 0·0·310 - 280·1·2 - 2·60·4 =
= 280·0·4 + 2·1·310 + 0·60·2 - 0·0·310 - 280·1·2 - 2·60·4 =
= 0 + 620 + 0 - 0 - 560 - 480 = -420
∆2 = 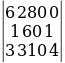 = 6·60·4 + 280·1·3 + 0·1·310 - 0·60·3 - 6·1·310 - 280·1·4 =
= 6·60·4 + 280·1·3 + 0·1·310 - 0·60·3 - 6·1·310 - 280·1·4 =
= 1440 + 840 + 0 - 0 - 1860 - 1120 = -700
∆3 = 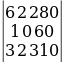 = = 6·0·310 + 2·60·3 + 280·1·2 - 280·0·3 - 6·60·2 - 2·1·310 =
= = 6·0·310 + 2·60·3 + 280·1·2 - 280·0·3 - 6·60·2 - 2·1·310 =
= 0 + 360 + 560 - 0 - 720 - 620 = -420
x = 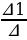 =
= 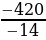 = 30
= 30
y = 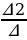 =
= 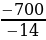 = 50
= 50
z = 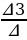 =
= 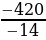 = 30
= 30
Таким образом, еженедельный объем выпускаемой продукции, с учетом запасов сырья, составит 30 шт перчаток, 50 шт – сумок и 30 шт – портмоне.
Заключение
В результате вышеизложенного хочется еще раз подчеркнуть, что финансовая грамотность включает в себя огромную математическую составляющую – математика дает весь необходимый аппарат для решения большинства жизненных задач, связанных с личными, семейными и производственными финансами.
Библиографический список
1. Башмаков М.И. Математика: учеб. для студентов учреждений сред. проф. образования. М.: Издательский центр «Академия», 2018.
2. Башмаков М.И. Математика: сборник задач профильной направленности: учеб. для студ. учреждений сред. проф. образования. М.: Издательский центр «Академия», 2018.
3. Алимов Ш.А. и др. Математика: Алгебра и начала математического анализа, геометрия. 10-11 классы. Учебник. Базовый и углубленный уровни. М.: Просвещение, 2018.
4. Мордкович А.Г. Алгебра и начала анализа. 10 класс для общеобразовательных учреждений (профильный уровень) часть 1, учебник. М. Мнемозина, 2017.
5. Мордкович А.Г. Алгебра и начала анализа. 10 класс для общеобразовательных учреждений (профильный уровень) часть 2, задачник. М. Мнемозина, 2017.
6. Кремер Н.Ш. Линейная алгебра: учебник и практикум / Н.Ш.Кремер, М.Н. Фридман; под ред. Н.Ш.Кремера. – М.: Издательство Юрайт, 2016–306с.
7. Жданова А.О., Савицкая Е.В. Финансовая грамотность: материалы для обучающихся. Среднее профессиональное образование. – М.: ВАКО, 2020.
16







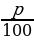 )N S, которая выражает функциональную зависимость вида y=ax.
)N S, которая выражает функциональную зависимость вида y=ax.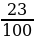 )N 1000000
)N 1000000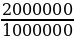
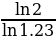 =
= 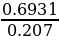 = 3.35.
= 3.35.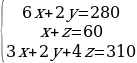
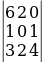 = 6·0·4 + 2·1·3 + 0·1·2 - 0·0·3 - 6·1·2 - 2·1·4 = 0 + 6 + 0 - 0 - 12 - 8 = -14
= 6·0·4 + 2·1·3 + 0·1·2 - 0·0·3 - 6·1·2 - 2·1·4 = 0 + 6 + 0 - 0 - 12 - 8 = -14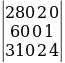 = 280·0·4 + 2·1·310 + 0·60·2 - 0·0·310 - 280·1·2 - 2·60·4 =
= 280·0·4 + 2·1·310 + 0·60·2 - 0·0·310 - 280·1·2 - 2·60·4 = 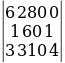 = 6·60·4 + 280·1·3 + 0·1·310 - 0·60·3 - 6·1·310 - 280·1·4 =
= 6·60·4 + 280·1·3 + 0·1·310 - 0·60·3 - 6·1·310 - 280·1·4 = 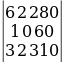 = = 6·0·310 + 2·60·3 + 280·1·2 - 280·0·3 - 6·60·2 - 2·1·310 =
= = 6·0·310 + 2·60·3 + 280·1·2 - 280·0·3 - 6·60·2 - 2·1·310 =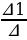 =
= 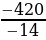 = 30
= 30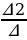 =
= 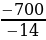 = 50
= 50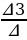 =
= 









