Исследовательская работа "Тригонометрия вокруг нас"

Содержание

Стр.

Введение……………………………………………..…………………....…...2

Ход проведённого исследования …………… ……………………....……..4

1. Исторические сведения ..............................................................................4

2. Тригонометрия а разных областях науки ………….………..…....…...…5

2.1. Тригонометрия в физике....................................................................... 5

2.2. Применение тригонометрии в архитектуре.….....…......................... 9

2.3. Тригонометрия в биологии………………………………..…..……...9

2.4. Тригонометрия в медицине………………………………………….10

3. Экспериментальная часть...........................................................................11

3.1 . Опрос учащихся по теме исследования..............................................11

3.2. Результаты опроса.................................................................................11

3.3. Проведение эксперимента...................................................................12

3.4. Результаты эксперимента....................................................................12

Заключение……………..………………………………………………….. 13

Литература ……………..……………………………………………….….. 14

Введение

На уроках геометрии в 8 и 9 классах мы познакомились с новыми для нас понятиями: синус, косинус, тангенс. Раздел математики, в котором изучаются эти функции, называется тригонометрией. При изучении тригонометрии мы все столкнулись с большими трудностями. Было очень сложно решать задания, непонятно, как строить рисунки, с чего начинать, и вообще, зачем это нужно!

Учитель, отвечая на этот вопрос, сказала, что тригонометрические функции играют огромную роль в нашей жизни, что многие реальные процессы окружающего мира описываются с помощью именно таких функций. Мне стало интересно, я захотела узнать побольше о тригонометрии. Честно говоря, я захотела разобраться в этой теме еще и потому, что вопросы по тригонометрии встречаются в ОГЭ по математике. Известно, что человек боится неизвестного, заранее настраивается на неудачу. Я хочу быть уверена, что с такими заданиями я смогу разобраться и решить их без особых затруднений и поэтому выбрала данную тему для своего исследования.

В моём исследовательском проекте «Тригонометрия вокруг нас» рассматривается практическое применение тригонометрических функций.

Приступая к написанию данной работы, я столкнулись с противоречием между имеющимися теоретическими знаниями по данной теме и отсутствием понимания того, где в реальной жизни можно встретиться с функциональной моделью, и как человек использует свойства тригонометрических функций в своей практической деятельности.

Объект исследования – тригонометрические функции; предмет исследования - области их практического применения.

Цель: выявить связь тригонометрических функций с явлениями окружающего мира и практической деятельностью человека, показать, что данные функции находит широкое применение в жизни.

Выбрав тему исследовательской работы и определив цель, мне необходимо было решить следующие задачи:

1. Изучить литературу и ресурсы удаленного доступа по теме проекта.

2. Выяснить, какие законы природы выражаются тригонометрическими функциями.

3. Найти примеры применения тригонометрических функций в окружающем мире.

4. Проанализировать и систематизировать имеющийся материал.

5. Подготовить оформленный материал в соответствии с требованиями информационного проекта.

6. Разработать в соответствии с содержанием проекта электронную презентацию.

7. Выступить на конференции с результатами проведённой работы.

Гипотеза исследования: аппарат математики, а именно тригонометрические функции, широко используется в других науках, а также находит практическое применение в жизни каждого человека.

Для решения этих задач исследовательской деятельности нужно использовать следующие методы:

• теоретические: изучение литературы, Интернет-ресурсов по данному вопросу.

• экспериментальный: проведение опроса среди учащихся и эксперимента по теме работы.

• логический анализ: метод систематизации накопленного материала.

Всю свою работу по данной теме я разделила на следующие этапы:

• Подготовительный, включающий в себя выбор темы исследования, постановку цели и задач, выбор методов изучения нашего объекта.

• Основной (информационно-поисковый), включающий в себя непосредственное изучение литературы, поиск ресурсов удалённого доступа, связанных с нашим проектом, проведение эксперимента.

• Заключительный этап, включающий в себя обработку изученного материала, анализ и систематизацию его. Подведение итогов. Подготовка доклада и презентации.

Ход проведённого исследования.

На подготовительном этапе я выдвинула гипотезу и сформулировала цель исследования, начала поиск необходимой информации, изучала литературу по теме, а также ресурсы удаленного доступа.

На основном этапе была подобрана и накоплена информация по теме, проанализированы найденные материалы. Я выяснили основные области применения тригонометрических функций. В течение месяца был проведен эксперимент с группой учащихся, а также был проведен опрос среди учащихся 8-9 классов. Все данные были обобщены и систематизированы.

На заключительном этапе разработан целостный окончательный вариант исследовательской работы, составлена презентация по теме исследования, проанализированная на предмет соответствия поставленным целям. На этом этапе также проводилась деятельность по реализации всех поставленных задач, подведение итогов и оценка своей деятельности.

1. Исторические сведения

Тригонометрия – раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии. Слово тригонометрия состоит из двух греческих слов: trigwnon - треугольник и metrew - измерять и в буквальном переводе означает измерение треугольников. Как и всякая другая наука, тригонометрия возникла в результате человеческой практики в процессе решения конкретных практических задач.

История тригонометрии началась более двух тысячелетий назад. Первоначально ее возникновение было связано с необходимостью выяснения соотношений углов и сторон треугольника. В процессе исследований выяснилось, что математическое выражение данных соотношений требует введения особых тригонометрических функций, которые первоначально оформлялись как числовые таблицы. Для многих смежных с математикой наук толчком к развитию стала именно история тригонометрии. Происхождение единиц измерения углов (градусов), связанное с исследованиями ученых Древнего Вавилона, опирается на шестидесятиричную систему исчисления, которая дала начала современной десятичной, применяемой во многих прикладных науках.

Предполагается, что изначально тригонометрия существовала как часть астрономии. Затем она стала использоваться в архитектуре. А со временем возникла целесообразность применения данной науки в различных областях человеческой деятельности. Это, в частности, астрономия, морская и воздушная навигация, акустика, оптика, электроника, архитектура и прочие.

Руководствуясь данными о сохранившихся научных реликвиях, исследователи сделали вывод, что история возникновения тригонометрии связана с работами греческого астронома Гиппарха, который впервые задумался над поиском способов решения треугольников (сферических). Его труды относятся ко 2 веку до нашей эры.

Также одним из важнейших достижений тех времен является определение соотношения катетов и гипотенузы в прямоугольных треугольниках, которое позже получило название теоремы Пифагора. История развития тригонометрии в Древней Греции связана с именем астронома Птоломея - автора геоцентрической системы мира, господствовавшей до Коперника. Греческим астрономам не были известны синусы, косинусы и тангенсы. Они пользовались таблицами, позволяющими найти значение хорды окружности с помощью стягиваемой дуги. Единицами для измерения хорды были градусы, минуты и секунды. Один градус приравнивался к шестидесятой части радиуса.

Значительных успехов достигли индийские средневековые астрономы. Гибель античной науки в IV веке обусловила перемещение центра развития математики в Индию. История возникновения тригонометрии как обособленного раздела математического учения началась в Средневековье. Именно тогда ученые заменили хорды синусами. Это открытие позволило ввести функции, касающиеся исследования сторон и углов прямоугольного треугольника. То есть именно тогда тригонометрия начала обосабливаться от астрономии, превращаясь в раздел математики. Первые таблицы синусов были у Ариабхаты, они была проведены через 3 , 4 , 5 градусов. Позже появились подробные варианты таблиц: в частности, Бхаскара привел таблицу синусов через 1градус.

Первый специализированный трактат по тригонометрии появился в X—XI веке. Автором его был среднеазиатский учёный Аль-Бируни. А в своем главном труде «Канон Мас‘уда» (книга III) средневековый автор еще более углубляется в тригонометрию, приводя таблицу синусов (с шагом 15') и таблицу тангенсов (с шагом 1°).

История тригонометрии в Европе связана с именем англичанина Ричарда Уоллингфордского, который стал автором сочинения «Четыре трактата о прямых и обращенных хордах». Именно его труд стал первой работой, которая целиком посвящена тригонометрии. К XV веку многие авторы в своих трудах упоминают о тригонометрических функциях. В Новое время большинство ученых стало осознавать чрезвычайную важность тригонометрии не только в астрономии и астрологии, но и в других областях жизни. Это, в первую очередь, артиллерия, оптика и навигация в дальних морских походах. Поэтому во второй половине XVI века эта тема заинтересовала многих выдающихся людей того времени, в том числе Николая Коперника, Иоганна Кеплера, Франсуа Виета. Коперник отвел тригонометрии несколько глав своего трактата «О вращении небесных сфер» (1543). Чуть позже, в 60-х годах XVI века, Ретик - ученик Коперника - приводит в своем труде «Оптическая часть астрономии» пятнадцатизначные тригонометрические таблицы.

Альбрехт Дюрер стал тем, благодаря кому на свет появилась синусоида. Придание тригонометрии современного содержания и вида стало заслугой Леонарда Эйлера. Его трактат 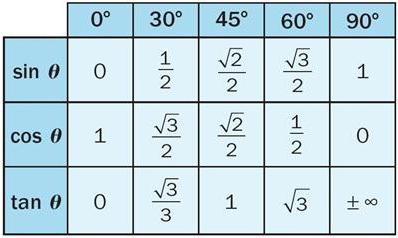«Введение в анализ бесконечных» (1748) содержит определение термина «тригонометрические функции», которое эквивалентно современному.

Понятие «синус» имеет очень долгую историю. Упоминания о различных отношениях отрезков треугольников и окружностей обнаруживаются еще в научных трудах, датируемых III веком до нашей эры. Работы таких великих древних ученых, как Евклид, Архимед, Апполоний Пергский, уже содержат первые исследования этих соотношений. Новые открытия требовали определенных терминологических уточнений. Так, индийский учёный Ариабхата дает хорде название «джива», означающее «тетива лука». Когда арабские математические тексты переводились на латынь, термин заменили близким по значению синусом (т. е. «изгиб»). Слово «косинус» появилось намного позже. Этот термин является сокращенным вариантом латинской фразы «дополнительный синус». Возникновение тангенсов связано с расшифровкой задачи определения длины тени. Термин «тангенс» ввел в X веке арабский математик Абу-ль-Вафа, составивший первые таблицы для определения тангенсов и котангенсов. Но европейские ученые не знали об этих достижениях. Немецкий математик и астроном Регимонтан заново открывает эти понятия в 1467 г. Доказательство теоремы тангенсов – его заслуга. А переводится этот термин как «касающийся».

2. Тригонометрия а разных областях науки

Восход и заход солнца, изменение фаз луны, чередование времен года, биение сердца, циклы в жизнедеятельности организма, вращение колеса, морские приливы и отливы, музыка - модели этих многообразных процессов описываются тригонометрическими функциями.

2. 1. Тригонометрия в физике.

В технике и окружающем нас мире часто приходится сталкиваться с периодическими (или почти периодическими) процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения. Наряду с поступательными и вращательными движениями тел в механике значительный интерес представляют и колебательные движения.

Механическими колебаниями называют движения тел, повторяющиеся точно (или приблизительно) через одинаковые промежутки времени. Закон движения тела, совершающего колебания, задается с помощью некоторой периодической функции времени x = f(t). Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне.

Примерами простых колебательных систем могут служить груз на пружине или математический маятник (рис.1).

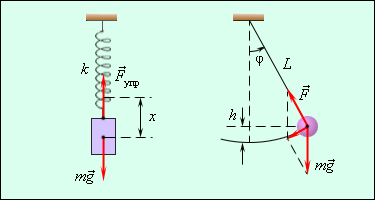
Рис.1. Механические колебательные системы.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются вынужденными.

На рисунке 2 приведены графики координаты, скорости и ускорения тела, совершающего гармонические колебания.

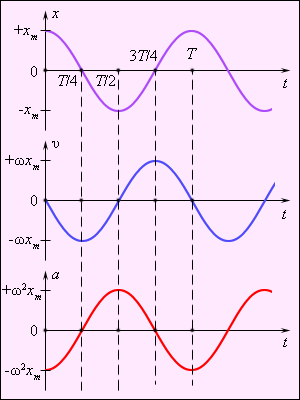Простейшим видом колебательного процесса являются простые гармонические колебания, которые описываются уравнением:

x = m cos (ωt + f₀).

Рис. 2. Графики координаты x(t), скорости υ(t)

и ускорения a(t) тела, совершающего

гармонические колебания.

Звуковыми волнами или просто звуком принято называть волны, воспринимаемые человеческим ухом.

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Если бы зрение людей обладало способностью видеть звуковые, электромагнитные и радиоволны, то мы видели бы вокруг многочисленные синусоиды всевозможных видов.

Когда световой луч проходит границу между менее плотной оптической средой, например воздухом, и более плотной оптической средой, например водой, часть светового луча не проникает внутрь новой среды, а отражается от ее поверхности. Другая же часть светового луча проникает внутрь, но, уже меняя направление. 

Это явление называется преломлением света, и ученые уже давно могут не просто наблюдать, но и точно рассчитывать угол этого преломления. Оказалось, что простейшие тригонометрические формулы и знание синуса угла падения и угла преломления дают возможность узнать постоянный коэффициент преломления для перехода светового луча из одной конкретной среды в другую. Например, коэффициент преломления воздуха чрезвычайно мал и составляет 1,0002926, коэффициент преломления воды чуть больше - 1,332986, алмаз преломляет свет с коэффициентом 2,419, а кремний - 4,010.

Данное явление лежит в основе, так называемой Теории радуги. Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.

Радуга возникает из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе по закону преломления:

,

где n₁=1, n₂≈1,33 – соответственно показатели преломления воздуха и воды, α – угол падения, а β – угол преломления света.

1. Применение тригонометрии в искусстве и архитектуре.

Детская школа Гауди в Барселоне.

Культовые здания во всем мире были спроектированы благодаря математике, которая может считаться гением архитектуры. Некоторые известные примеры таких зданий: Детская школа Гауди в Барселоне, Небоскрёб Мэри-Экс в Лондоне, Винодельня «Бодегас Исиос» в Испании, Ресторан в Лос-Манантиалесе в Аргентине. При проектировании этих зданий не обошлось без тригонометрии.

2.3. Тригонометрия в биологии.

Одно из фундаментальных свойств живой природы - это цикличность большинства происходящих в ней процессов. Между движением небесных тел и живыми организмами на Земле существует связь. Живые организмы не только улавливают свет и тепло Солнца и Луны, но и обладают различными механизмами, точно определяющими положение Солнца, реагирующими на ритм приливов, фазы Луны и движение нашей планеты.

Биологические ритмы, биоритмы, - это более или менее регулярные изменения характера и интенсивности биологических процессов. Способность к таким изменениям жизнедеятельности передается по наследству и обнаружена практически у всех живых организмов. Их можно наблюдать в отдельных клетках, тканях и органах, целых организмах и популяциях. Биоритмы подразделяют на физиологические, имеющие периоды от долей секунды до нескольких минут и экологические, по длительности совпадающие с каким либо ритмом окружающей среды. К ним относят суточные, сезонные, годовые, приливные и лунные ритмы. Основной земной ритм – суточный, обусловлен вращением Земли вокруг своей оси, поэтому практически все процессы в живом организме обладают суточной периодичностью.

Множество экологических факторов на нашей планете, в первую очередь световой режим, температура, давление и влажность  воздуха, атмосферное и электромагнитное поле, морские приливы и отливы, под влиянием этого вращения закономерно изменяются.

Вы замечали, что в определенные периоды ваша жизнь делает необъяснимые скачки? Вдруг откуда не возьмись  - бьют через край эмоции. Повышается чувствительность, которая внезапно может смениться полной апатией. Творческие и бесплодные дни, счастливые и несчастные моменты, резкие скачки настроения. Подмечено, что возможности человеческого организма меняются периодически. Эти знания лежат в основе «теории трех биоритмов».

Физический биоритм – регулирует физическую активность. В течение первой половины физического цикла человек энергичен, и достигает лучших результатов в своей деятельности (вторая половина – энергичность уступает лености).

Эмоциональный ритм – в периоды его активности повышается чувствительность, улучшается настроение. Человек становится возбудимым к различным внешним катаклизмам. Если у него хорошее настроение, он строит воздушные замки, мечтает влюбиться и влюбляется. При снижении эмоционального биоритма происходит упадок душевных сил, пропадает желание, радостное настроение.

Интеллектуальный биоритм - он распоряжается памятью, способностью к обучению, логическому мышлению. В фазе активности наблюдается подъем, а во второй фазе спад творческой активности, отсутствуют удача и успех.

Теория трех ритмов.

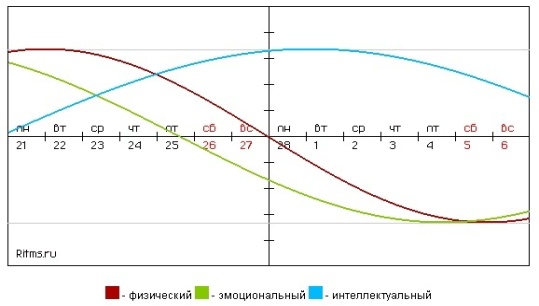• Физический цикл -23 дня. Определяет энергию, силу, выносливость, координацию движения

• Эмоциональный цикл - 28 дней. Состояние нервной системы и настроение

• Интеллектуальный цикл - 33 дня. Определяет творческую способность личности

2.4. Тригонометрия в медицине.

В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.

Формула, получившая название тегеранской, была представлена широкой научной общественности на 14-й конференции географической медицины и затем - на 28-й конференции по вопросам применения компьютерной техники в кардиологии, состоявшейся в Нидерландах.

Эта формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.

Многим людям приходится делать кардиограмму сердца, но немногие знают, что кардиограмма человеческого сердца – график синуса или косинуса.

Тригонометрия помогает нашему мозгу определять расстояния до объектов. Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Такой вывод был сделан после серии экспериментов, участникам которых предлагалось взглянуть на окружающий мир через призмы, увеличивающие этот угол.

Результаты нового исследования, как можно предположить, окажутся небезынтересны инженерам, конструирующим системы навигации для роботов, а также специалистам, которые работают над созданием максимально реалистичных виртуальных моделей. Возможны и приложения в области медицины, при реабилитации пациентов с повреждениями определенных о бластей мозга.

1. Экспериментальная часть

1. Опрос учащихся по теме исследования

Среди учащихся 8-11 классов нашей школы был проведен опрос. Ребятам были розданы опросные листы, включающими 10 вопросов по теме исследования следующего содержания: (Приложение 1)

1. Результаты опроса

По результатам опроса составлены диаграммы (Приложение 2)

1. Проведение эксперимента по выявлению влияния тригонометрических функций на жизнь человека

Среди опрошенных учащихся были отобраны желающие участвовать в эксперименте.

Эксперимент состоял в том, что в течение месяца ребята оценивали свое физическое, эмоциональное и интеллектуальное самочувствие по шкале от 0 до 5 баллов. Никаких инструкций испытуемые не получали и оценивали свое состояние по своему усмотрению. Каждый вечер они присылали мне свои оценки по телефону. Я завела на каждого участника отдельную таблицу и постепенно заполняла таблицы этими оценками. Смысл эксперимента состоит в том, чтобы доказать на нашем личном примере влияние тригонометрической функции синус на наше собственное самочувствие. В конце эксперимента мы должны убедиться, что результаты измерений биоритмов совпадают с синусоидами, которые построены математическим путем по дате рождения участников. Допускается некоторое расхождение реального графика с математическим, так как оценка своего самочувствия не всегда объективна. Для полноты эксперимента берется не один человек, а группа из 8 человек.

1. Результаты эксперимента

Для каждого участника эксперимента я построила графики по следующим правилам:

1. График по дате рождения показывает математические колебания трех составляющих самочувствия от – 100 до +100. (Приложение 3)

2. График колебаний этих же биоритмов по показаниям участников по шкале от 0 до 5. Всего было проведено 15 измерений для 8 человек, т. е получено 120 результатов.

3. Для каждого участника данные сопоставляются, и ищутся совпадения, чтобы увидеть их сходство или различия. Всего получено 60 совпадений.

4. Делается вывод: В 50% измерений получены совпадения личной оценки биоритмов с оценкой, полученной научным путем. Я считаю, что данный эксперимент подтвердил нашу гипотезу о большой роли тригонометрических функций в жизни людей.

Заключение

В настоящее время тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников. Также следует отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел, сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

Выводы:

• Я выяснила, что тригонометрия была вызвана к жизни необходимостью производить измерения углов, но со временем развилась в науку о тригонометрических функциях.

• Я показала, что тригонометрия тесно связана с физикой, биологией, применяется в архитектуре и медицине.

• В результате проведенного эксперименты было доказано, что тригонометрические функции играют большую роль в жизни каждого человека, т. к. функция синус описывает периодические изменения трех составляющих самочувствия.

• Я думаю, что тригонометрия нашла отражение в нашей жизни, и сферы, в которых она играет важную роль, будут расширяться.

• Я лучше стала понимать тригонометрические понятия и отношения и в будущем постараюсь осваивать материал данного раздела математики полностью.

Литература

1. Л. С. Атанасян. Геометрия. Учебник для 7-9 кл. общеобразовательных учреждений –М.: Просвещение, 2015.

2. Виленкин Н.Я. Функции в природе и техники: Кн. для внеклас. чтения IX-XX кл. – 2-е изд., испр.-М: Просвещение, 1985.

3. Глейзер Г.И. История математики в школе: IX-X кл. — М.: Просвещение, 1983.

4. И. М. Гельфанд, С.М. Львовский, А. Л. Тоом ТРИГОНОМЕТРИЯ учебное пособие для учащихся 10 кл. общеобразовательных учреждений.– М.: МЦНМО АО «Московские учебники», 2002.

5. Маслова Т.Н. «Справочник школьника по математике»

6. Рыбников К.А. История математики: Учебник. — М.: Изд-во МГУ, 1994.

7. Math.ru «библиотека».