Исследовательская работа "Удивительное умножение"

РАЙОННАЯ НАУЧНО-ПРАКТИЧЕСКАЯ КОНФЕРЕНЦИЯ ОБУЧАЮЩИХСЯ

«НАУКА. ТВОРЧЕСТВО. РАЗВИТИЕ»,

посвящённая Году добровольца и волонтера в России,

в 2017-2018 учебном году

Секция

«ЧЕЛОВЕК И НАУКА»

«Удивительное умножение»

(исследовательская работа)

Булатова Ксения Александровна,

обучающаяся 8 класса

МКОУ «Барановская СОШ»

Научный руководитель:

Дюкина Елизавета Разифовна,

учитель математики

МКОУ «»Барановская СОШ

апрель 2018 г.

Оглавление

Введение…………………………………………………………………………….…3

Глава 1. Теоретические аспекты исследования ……………......……..…………….5

1. Как люди научились считать...…………………………………………….5

2. Крестьянский способ умножения ..………………………………………..7

3. Умножение на пальцах …………………………………………………….9

4. Китайский (графический) способ умножения…………………………...10

5. Итальянский способ умножения …………….……………….…………..11

6. Умножение «Способом молнии»…………………………………………12

7. Умножение «Крест - накрест»……………………………………………13

Глава 2. Практические аспекты исследования…….………………..……………...14

Заключение …………………………………………………………….………..…...17

Список использованных источников и литературы……………………………….18

Приложения…………………………………………………………………………..19

Введение

«Предмет математики настолько серьезен,

что полезно не упускать случаев делать

его немного занимательным».
Б. Паскаль

Ни один человек на свете не может обойтись без вычислений. Поэтому на уроках математики нас в первую очередь учат производить действия над числами: складывать, вычитать, умножать и делить.

Во втором классе все дети начальной школы начинают изучать таблицу умножения. Кому-то она дается легко, но есть и те, кто испытывает некоторые затруднения, чтобы понять и выучить ее. В школе нас знакомят с привычными способами умножения.

Проблемность исследования. Постоянное применение современной вычислительной техники приводит к тому, что учащиеся затрудняются производить какие-либо расчеты, не имея в своем распоряжении таблиц или счетной машины.

Актуальность. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результате механизированных вычислений. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического цикла.

Исходя из этого, возник вопрос, существуют ли другие способы вычислений? Мы предположили, наверное, существуют. Вследствие чего появилось желание изучить их более подробно. В поисках ответа на возникшие вопросы было проведено данное исследование.

Также, чтобы заинтересовать своих одноклассников, было решено показать им интересные способы умножения.

Цель исследования: изучить необычные способы умножения, не рассматриваемые в школьном курсе математики.

Задачи:

- изучить литературу по данной теме;

- найти необычные способы умножения;

- научиться их применять;

- выбрать самые интересные или более легкие и использовать их при счете.

Объект исследования: нестандартные способы умножения.

Предмет исследования: процесс вычисления нестандартными способами умножения.

Методы: - поисковый метод: изучение литературы, поиск необходимой информации в сети Интернет;

- практический метод: выполнения вычислений с применением нестандартных способов.

Практическая значимость исследования заключается в том, что данный материал может быть использован на уроках математики, а также при подготовке домашнего задания.

Глава 1. Теоретические аспекты исследования

1.1. Как люди научились считать

Никто не знает, как впервые появилось число, как первобытный человек начал считать. Десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Постепенно возникала необходимость отвечать на жизненно важные вопросы: по сколько плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас, сколько нужно сделать ножей и т.п. Таким образом, сам не замечая, человек начал считать и вычислять.

Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов – одного птенца и т.д. Научившись выделять один предмет из множества других, говорили «один», а если их было больше – «много». Даже для названия числа «один» часто пользовались словом, которым обозначался единичный предмет, например «луна», «солнце». Такое совпадение названия предмета и числа сохранилось в языке некоторых народов до наших дней.

Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки) привели человека к представлению о числе два. До сих пор слово «два» на некоторых языках звучит так же, как «глаза» или «крылья».

Если предметов было больше двух, то первобытный человек говорил «много». Лишь постепенно человек научился считать до трёх, затем до пяти и до десяти и т.д. Название каждого числа отдельным словом было великим шагом вперёд.

До появления цифр или букв, которые используются как цифры, люди считали на пальцах или с помощью камней, раковин, зарубок, узлов. Понятие считать – calculare по-латыни (откуда современные слова калькулировать, калькулятор), произошло от латинского же слова calaulus, камешек.

Единственными доступными математическими действиями на протяжении очень долгого времени были сложение и вычитание. Затем освоили умножение, которое, по сути, было просто удвоением и дальнейшим сложением. Потребность в умножении появилась в связи с необходимостью вычисления площадей. У египтян и вавилонян умножение называлось «а-ша», это же слово означает площадь. Арабы в средневековых математических сочинениях умножение называют « сатх », а это то же самое, что и поверхность (прямоугольника).

В Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.

Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. Если бы современный школьник попал в прошлое, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.

Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления – приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия. За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своем трактате «Сумма знаний по арифметике, отношениям и пропорциональности» (1494г.) приводит 8 различных методов умножения. В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» изложено 27 способов умножения. На данный момент способов умножения чисел насчитывается более сорока.

В огромном мире людей с давних пор известны обладатели феноменальных способностей устного счета. Ими владели многие ученые, например, Андре Ампер и Карл Гаусс. А также и многие люди, чья профессия была далека от математики и науки в целом. Ранее на эстраде были популярны выступления специалистов в устном счете. Иногда они устраивали между собой показательные соревнования, проводившиеся, в том числе и в стенах уважаемых учебных заведений, таких как Московский государственный университет имени М. В. Ломоносова.

Начиная с 2004 года, один раз в два года проводится Мировой чемпионат по вычислениям в уме, на который собираются лучшие из ныне живущих феноменальных счётчиков планеты.

Разработкой приемов быстрого счета занимались многие ученые: Яков Исидорович Перельман, Георгий Берман, Я. Трахтенберг и другие.

Известна необычная история создания целой системы повышения быстроты счета. Она создана была в годы второй мировой войны профессором математики Я. Трахтенбергом. Она известна под названием "Системы быстрого счета". В 1941 году гитлеровцы бросили Трахтенберга в концлагерь. Чтобы уцелеть в нечеловеческих условиях и сохранить нормальной свою психику, Трахтенберг начал разрабатывать принципы ускоренного счета. За четыре страшных года пребывания в концлагере профессору удалось создать стройную систему ускоренного обучения детей и взрослых основам быстрого счета. После войны Трахтенберг создал и возглавил Цюрихский математический институт, получивший мировую известность.

Предлагаем рассмотреть наиболее интересные и простые способы умножения.

1.2. Крестьянский способ умножения

Этот способ использовали русские крестьяне, который был унаследован ими от глубокой древности. Он основан на знание таблицы умножения на два. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1. Последнее удвоенное число и дает искомый результат.

Пример 1. Вычислить 37 ∙ 32 =

32 37

16 74

8 148

4 296

2 592

1 1184

37 ∙ 32 = 1184 ∙ 1 = 1184

Однако как поступить, если при этом приходится делить пополам нечётное число? В этом случае от нечётного числа откидываем единицу и делим остаток пополам, при этом к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечётных чисел левого столбца – сумма и будет искомым произведением.

Иными словами все строки с чётными левыми числами зачёркиваем; оставляем только с нечётными левыми числами, а затем суммируем
не зачёркнутые числа правого столбца.

Пример 2. Вычислить 24 ∙ 17 =

17 24

8 48

4 96

2 192

1 384

24 ∙ 17 = 384 + 24 = 408

Данный способ удобен для тех людей, которые умеют легко умножать и делить на два. Трудность возникает, если встречаются нечетные числа, надо быть очень внимательным. Чем больше числа, тем дольше вычисления.

1.3. Умножение на пальцах

Способность умножать с помощью пальцев – ценный навык, который известен человечеству как минимум с XV века. Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета «единицами», «парами», «тройками», «четверками», «пятерками» и «десятками». Пальцы рук здесь служили вспомогательным вычислительным устройством.

Такой способ будет полезен для школьников, которые только начинают изучать умножение. Для успешного использования данного способа необходимо знать таблицу умножения от одного до пяти. Метод с пальцами рук заменяет таблицы умножения на шесть, семь, восемь, девять и десять.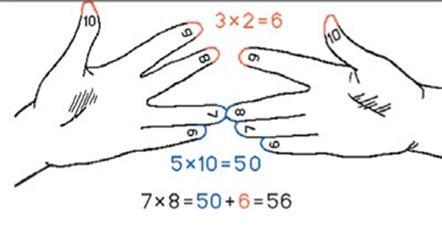

Алгоритм умножения на пальцах:

Рис. 1. Умножение на пальцах 1) Держите руки так, чтобы ладони были повернуты к телу, а пальцы располагались друг напротив друга. 

Каждый палец будет соответствовать числу. Мизинцы соответствуют числу 6, безымянные пальцы – числу 7, средние пальцы – числу 8, указательные пальцы – числу 9, а большие пальцы соответствуют числу 10.

2) Соприкоснитесь пальцами, которые соответствуют нужным числам.

Например, чтобы решить пример 7x8 (рис. 1), коснитесь левым безымянным пальцем среднего пальца правой руки. Пальцы левой руки будут соответствовать числу с левой стороны от знака умножения, а пальцы правой руки – числу с правой стороны от знака умножения. Не забывайте, что каждый палец соответствует своему числу, а в данном примере безымянный палец соответствует числу 7, а средний – числу 8.

3) Сложите пальцы, которые соприкасаются, а также пальцы под ними.

Теперь вам нужно посчитать соприкасающиеся пальцы и те пальцы, что находятся ниже. Они соответствуют десяткам. В нашем примере считаем безымянный палец на левой руке, мизинец на левой руке и средний, безымянный пальцы и мизинец на правой руке (2+3=5). Каждый из пальцев учитывается как число 10. В нашем случае получаем: 5*10=50.

4) Умножьте оставшиеся пальцы. 

Сначала подсчитайте количество пальцев на левой руке, которые находятся выше соприкасающихся пальцев, в нашем случае – это 3. Затем сосчитайте количество пальцев на правой руке выше соприкасающихся пальцев, в нашем случае это 2. 3x2 = 6.

5) Сложите два числа вместе, чтобы узнать ответ. В нашем примере необходимо сложить 50 и 6. В итоге получилось 56.

1.4. Китайский (графический) способ

Его цель заключается в том, чтобы, не зная таблицы умножения можно  без ошибок умножать числа. Числа изображаются линиями «палочками» и считаются пересечения линий.

Алгоритм умножения (на примере двузначных чисел):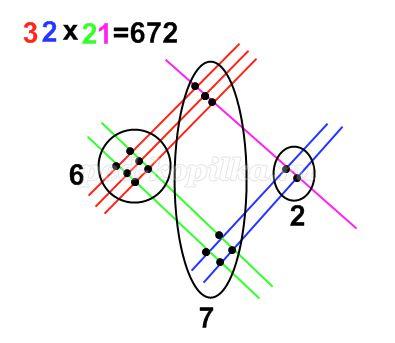

Пример 1. Предположим надо умножить 32 на 21 (рис. 2).

1.На листе бумаги поочередно рисуем линии, количество которых определяется из данного примера.

Рисуем первое число – 32. Для этого сверху вниз, слева на право, рисуем: три красные палочки (3)и две синих (2).

Рис. 2. Графический способ Рисуем второе число – 21, снизу вверх, слева направо: две зеленых палочки (2); одну сиреневую (1).

2. Теперь простым карандашом отделяем самые левые точки пересечения, самые правые, и остаётся середина, и приступим к их подсчёту. Двигаемся справа налево (по часовой стрелке): 2, 7, 6.

Полученный результат прочитаем слева направо – 672.

Изобразить первое число: начертить две группы палочек - число десятков, чуть отступив под таким же углом - число единиц.

Пример 2.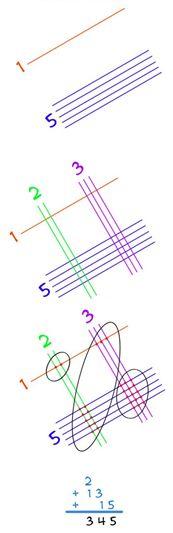

Умножим 15 на 23 (рис. 3).

1) Первое число 15:

рисуем первую цифру – одной линией;

рисуем вторую цифру – пятью линиями.

2) Второе число 23:

рисуем первую цифру – двумя линиями;

рисуем вторую цифру – тремя линиями.

3) Подсчитываем количество точек в группах:

первая группа слева – 2 (сотни);

вторая группа диагональ – 13 (десятки);

третья группа справа – 15 (единицы).

4) Результат – 345.

Рис. 3. Умножение 15 на 23

1.5. Итальянский способ умножения

Итальянский способ умножения был распространен в средние века на Востоке и Италии. Также способ носит романтическое название «ревность», или «решётчатое умножение».

Алгоритм умножения итальянским способом.

Сначала рисуем прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, - пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».

Умножаем, например, 6827 на 345:

1. Вычерчиваем квадратную сетку и пишем один из номеров над колонками, а второй по высоте (рис. 4).

Рис. 4. Умножение 6827 на 345. Сетка №1

2. Изобразив сетку, умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 3 на 6, на 8, на 2 и на 7. Первая цифра получившегося при умножении числа пишется вверху, вторая – внизу. Если при умножении получилось однозначное число, то записываем его вниз, а вверху пишем 0, например, 06 (рис. 5).

Рис. 5. Умножение 6827 на 345. Сетка №2

3. Так выглядит сетка со всеми заполненными клетками (рис. 6).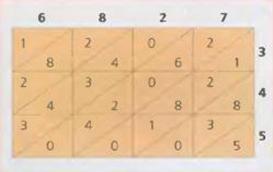

Рис. 6. Умножение 6827 на 345. Сетка №3

4. В заключение складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали (рис. 7).

Рис. 7. Умножение 6827 на 345. Сетка №4

Из результатов сложения цифр по диагоналям (они выделены жёлтым фоном) по направлению вниз-вправо составляется число 2355315, которое и является произведением чисел 6827 и 345, то есть 6827 х 345 = 2355315.

1.6. Умножение «Способом молнии»

В одной старинной русской рукописи описывается интересный прием «умножения крестиком», применявшийся еще в древней Индии под названием «молниеносного».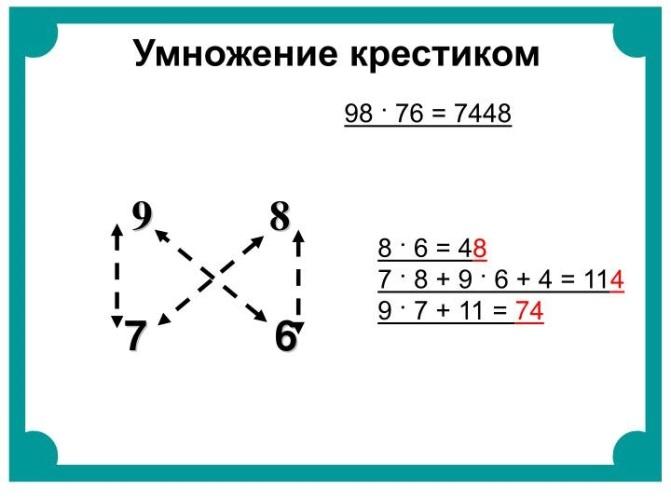

Пример: 98 х 76 = 1173 (рис. 8)

9 8

X

7 6

Последовательно производим следующие действия:

1) 8 х 6 = 48. 8 – это последняя цифра

Рис. 8. Умножение крестиком результата, 4 – запоминаем.

2) 7 х 8 +9 х 6 +4 = 114. 4 – предпоследняя цифра в ответе, 11 – запоминаем.

3) 9 х 7 +11= 74 – это первые цифры в ответе.

Ответ: 7448.

1. Умножение «Крест–накрест»

Например, умножим 94 на 97 (рис. 9).

Под каждым из чисел напишем дополнение до ста (т.е. сколько не хватает до 100). Числу 94 до ста не хватает 6, числу 97 не хватает 3. Соединяем числа крест-накрест.

Выберем любой из множителей (93 или 94). Допустим 94, противоположное число 3, вычитаем, получается 91, это первая цифра ответа. Вторая цифра равна произведению остатков 6*3=18.

Ответ 9118.

Рис. 9. Умножение «Крест-накрест»

Глава 2. Практические аспекты исследования

Для того чтобы выяснить, знают ли современные школьники другие способы умножения кроме умножения столбиком, был проведен опрос. Было опрошено 16 учащихся 5-9 классов. Для опроса были составлены следующие вопросы:

• Необходимо ли современному человеку уметь выполнять умножение?

• Умеете ли вы умножать?

• Знаете ли вы другие способы умножения кроме умножения в столбик?

• Хотели бы вы узнать другие способы умножения? (Приложение 1)

Обработав полученный материал, были составлены следующие результаты.

В результате исследования выяснилось, что все опрошенные считают, что современному человеку необходимо уметь выполнять умножение и умеют умножать. Также выяснилось, что о других способах умножения знают 6 опрошенных (38%) и 13 опрошенных (81%) хотят узнать о других способах.

На факультативных занятиях рассмотренные выше способы были представлены одноклассникам (Приложение №2). Все ребята с интересом слушали и вникали в суть каждого способа. Большинству одноклассников они понравились, и им тоже захотелось научиться умножать необычным способом, что привело на мысль о создании учебного пособия для учащихся 5-9 классов о необычных способах умножения. (Приложение 3)

Большинству одноклассников (5 чел.) понравился «Крестьянский» способ. Также были отмечены способы: «Итальянский», «Умножение на пальцах», «Китайский» и «Способ молнии».

Заключение

В истории математики есть много интересных событий и открытий, к сожалению, не вся эта информация доходит до нас, современных учеников. При выполнении исследовательской работы мне понадобились не только те знания, которые имеются у меня, но и необходимая работа с дополнительной литературой.

В ходе исследования были изучены различные источники информации по теме, анализ которых показал, что существуют различные необычные способы умножения, достаточно быстрые и надежные. Мы познакомились с нетрадиционными способами умножения, такими как «Крестьянский», «Китайский (графический)», «Итальянский», «Способ молнии», «На пальцах», «Крест-накрест».

Ранее признавалось, что для овладения искусством быстрого и безошибочного умножения многозначных чисел нужно особое природное дарование, исключительные способности; рядовым людям премудрость эта недоступна.
Своей работой мы доказали, что не нужно обладать сверхъестественными способностями, чтобы уметь пользоваться старинными способами умножения. Есть способы умножения чисел, для которых достаточно наличие карандаша и бумаги.

В результате исследования подтвердилась его актуальность: существует потребность учащихся в ознакомлении с другими способами умножения и применении их при вычислениях.

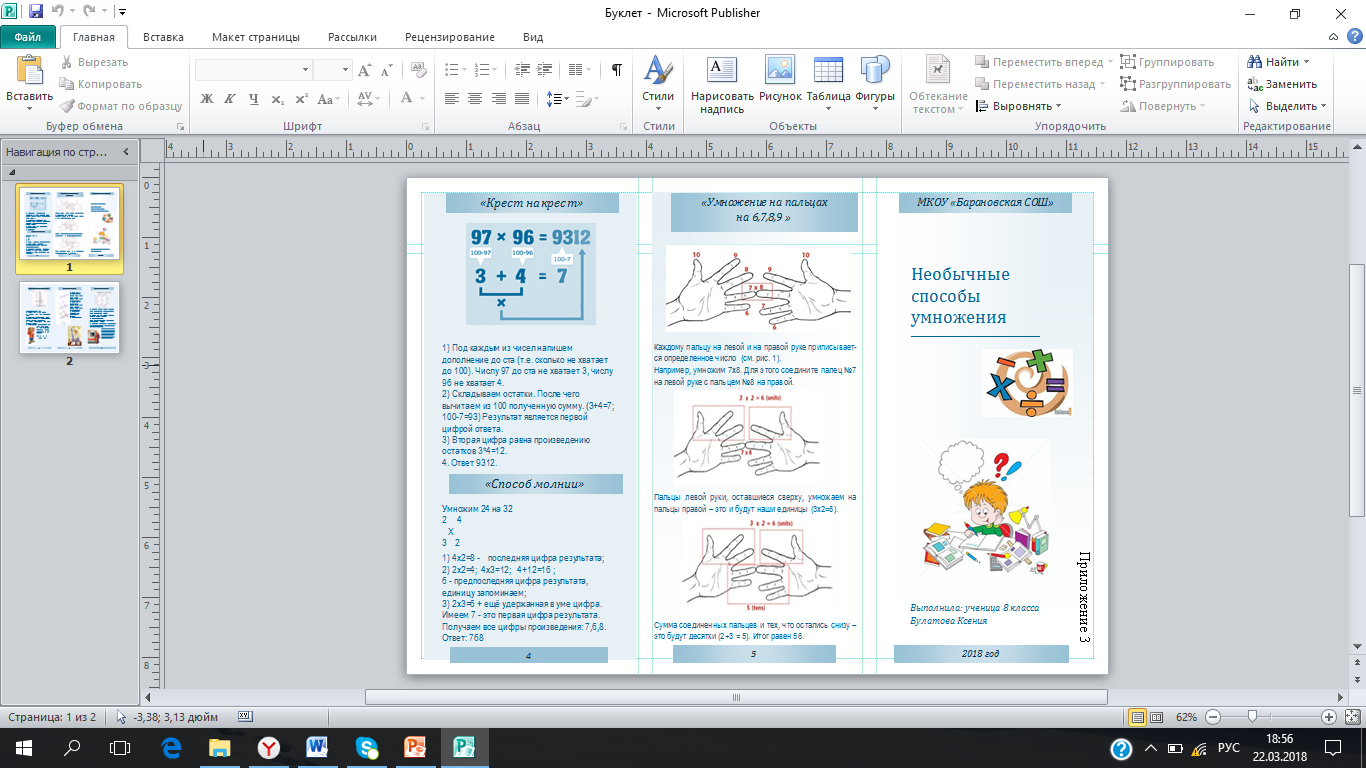
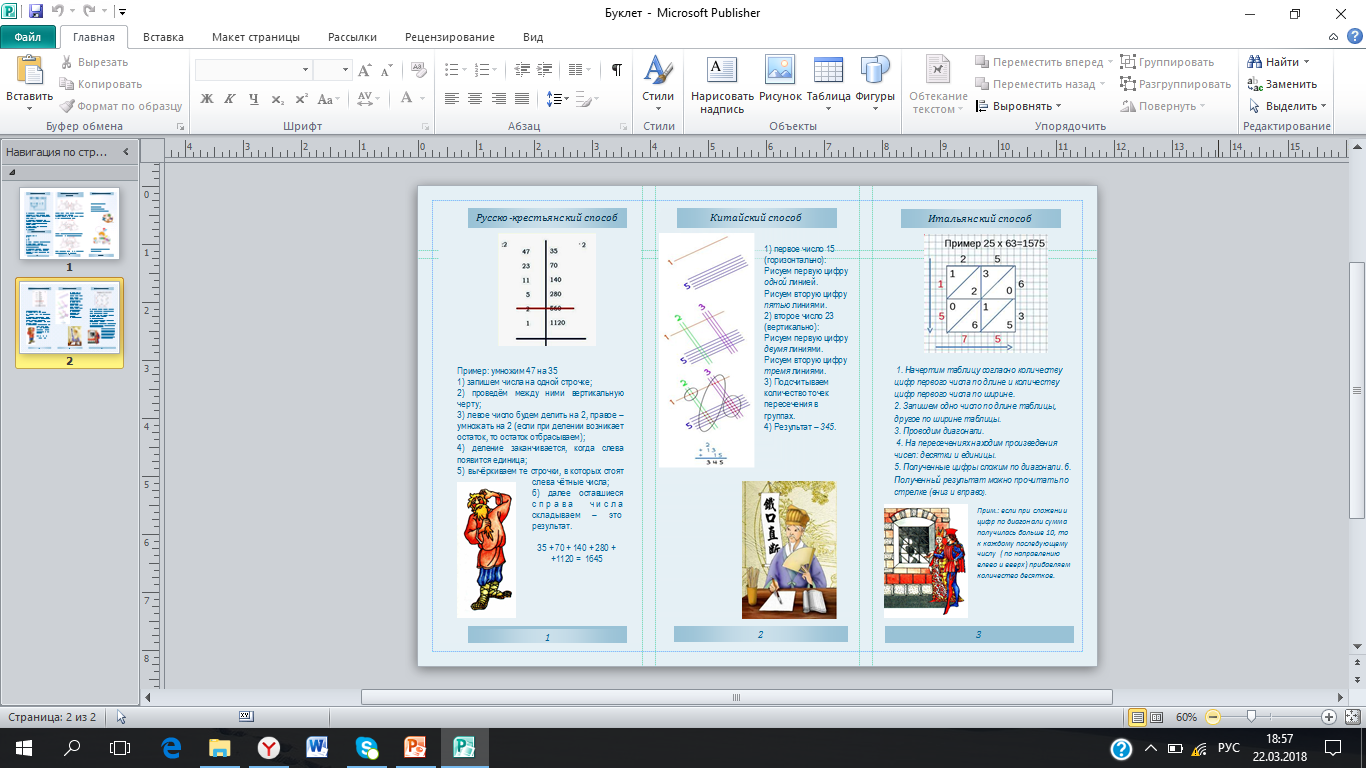
Результатом нашей работы стал буклет «Необычные способы умножения». Смело рекомендуем его вниманию любителей арифметики.

Список использованных источников и литературы

1. Депман И. «Рассказы о математике». – Ленинград.: Просвещение, 1954.–140с.

2. Олехник С. Н., Нестеренко Ю. В., Потапов М. К. «Старинные занимательные задачи». – М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.

3. Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с.

4. Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004.

5. Китайско-Японская система умножения. http://uk-optimist.ru/spravka/obmen-opytom/450-kitajsko-yaponskaya-sistema-umnozheniya

6. Корнеев А.А. Феномен русского умножения. История. http://numbernautics.ru/

7. Нетрадиционные способы умножения многозначных чисел. http://ped-kopilka.ru/blogs/ana-valerevna-demeshko/netradicionye-sposoby-umnozhenija-mnogoznachnyh-chisel.html

Приложение 1

Вопросы анкетирования

1. Необходимо ли современному человеку уметь выполнять умножение? (да/нет)

2. Умеете ли Вы умножать? (да/нет)

3. Знаете ли Вы другие способы умножения кроме умножения в столбик? (да/нет)

4. Хотели бы Вы узнать другие способы умножения? (да/нет)

Приложение 3

Буклет «Необычные способы умножения»