Исследовательский проект "Графический способ умножения чисел"

Республиканский конкурс исследовательских работ

в рамках Малой академии наук школьников

Исследовательская работа

«Графический способ умножения чисел»

Работу выполнила ученица 6 класса

МОБУ СОШ с. Воскресенское

МР Мелеузовский район

Республики Башкортостан

Горячкина Юлия

Руководитель учитель математики

Кувайцева Е.К.

2018 г.

Содержание

Введение

1. История возникновения умножения в Японии

2. «Японский» способ умножения

3. Умножение чисел с «0» в записи числа

4. Умножение десятичных дробей

5. Проведение эксперимента

Заключение

Список литературы

«Предмет математики настолько

серьезен, что полезно не упускать

случаев делать его немного занимательным». Б. Паскаль

Введение

Можно ли представить мир без чисел? Без чисел ни покупки не сделаешь, ни времени не узнаешь, ни номера телефона не наберёшь. А космические корабли, лазеры и все другие технические достижения?! Они были бы попросту невозможны, если бы не наука о числах.

Умножение чисел сейчас изучают в начальной школе. А вот в средние века совсем немногие владели искусством умножения.

Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.

За тысячелетия развития математики было придумано множество способов умножения чисел. Мы же не сможем выполнить умножения многозначных чисел - хотя бы даже двузначных - если не будем помнить наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения. В старинной «Арифметике» Магницкого необходимость твердого знания таблицы умножения воспета в таких - надо сознаться, чуждых для современного слуха - стихах:

Аще кто не твердит

таблицы и гордит,

Не может познати

числом что множати

И во всей науки, несвобод от муки,

Колико не учиттунеся удручит

И в пользу не будет аще ю забудет.

Сам Магницкий, автор этих стихов, очевидно, не знал или упустил из виду, что существуют способы перемножать числа и без знания таблицы умножения. Способы эти, не похожи на наши школьные приемы, некоторые употреблялись в обиходе великорусских крестьян и унаследованы ими от глубокой древности, некоторые используются и в наше время.

В школе изучают таблицу умножения, а затем учат детей умножать числа в столбик. Разумеется, это не единственный способ умножения. На самом деле, существует несколько десятков способов умножения многозначных чисел. В данной работе мы рассмотрим графический способ умножения, возможно он покажется более простым и вы будете им пользоваться.

Цель исследования

Изучить графический (японский) способ умножения, для производства которого достаточно умения складывать числа и применения карандаша, ручки и бумаги.

Гипотеза исследования

Существует способ умножения чисел, для которого достаточно наличие карандаша, бумаги и правил сложения.

Задачи исследования:

1. Познакомиться с графическим (японским) способом умножения чисел

2.Рассмотреть много примеров на применение данного метода

3. Рассказать о новом способе умножения и научить пользоваться им учащихся.

4. Провести эксперимент.

Методы:

- поисковый метод с использованием научной и учебной литературы, интернета;

- исследовательский метод при определении способа умножения чисел с 0 в записи числа;

- практический метод при решении примеров.

1. История возникновения умножения в Японии

Математика – царица наук. Мы начинаем изучать ее с самого раннего детства, пересчитывая пальчики, учась различаем предметы по размерам, определяя их геометрическую форму. И эти простые действия кажутся нам легко доступными для понимания. Но все меняется, когда мы идем в школу… Начинается все с таблицы умножения. Помните, как тяжело было запомнить эти нудные и однообразные примеры, понять которые было просто невозможно? Каждый день нам приходилось зазубривать их, и именно с этого момента многие начинали просто ненавидеть математику.

Японцы же придумали удивительный способ умножения, который не предполагает обязательное знание таблицы умножения. Теперь можно легко умножать двухзначные и трехзначные числа, даже не зная таблицы умножения.

Археологами в Японии была найдена деревянная табличка с фрагментом таблицы умножения, которая предположительно была изготовлена в VIII веке.

Рис.1

Учёные полагают, что подобные таблицы использовались японскими императорскими чиновниками, которым было необходимо осваивать разные науки, в том числе и арифметику. Обнаруженная табличка - самая древняя из всех найденных в Японии ранее. Интересно, что иероглифы, которыми записаны цифры, по стилю графического начертания очень похожи на те, которые использовались как официальное письмо во времена китайской династии Тан VII-X века. Исходя из этого, ученые предположили, что таблица была скопирована из китайского учебника арифметики того времени, то есть вся японская таблица умножения была заимствована из Китая.

Именно к своим соседям в Китай ездили высокопоставленные японцы каждый год, чтобы перенять у них разные науки, такие как арифметику. Древняя китайская таблица умножения была не из простых, так как включала в себя умножение двузначных чисел друг на друга. Вряд ли все японские чиновники могли выучить такую таблицу наизусть, поэтому и носили с собой на работу что-то типа шпаргалок, фрагмент одной из которых и представляет собой найденная археологами в Японии табличка.

Итак, японская таблица умножения была заимствована у китайцев, которые, согласно некоторым гипотезам, и были одними из создателей первой арифметической системы, о чем свидетельствуют археологические находки, содержащие фрагменты таблицы умножения, возраст которых ученые оценили в 2700-3000 лет.

Известно, что у японцев, китайцев и других наций, использующих иероглифы другой тип мышления нежели у нас. Они визуалы по природе. Иероглифы у них обозначают сразу какое-то слово и фразу. Доказано, что эти иероглифы воспринимаются человеком как образы. В подтверждение к этому, умножают они тоже интересно. 

1. «Японский» способ умножения

Представим метод умножения, бурно обсуждаемый в Интернете, который называют японским.

Умножение чисел по-японски выглядит иначе: оно имеет графическое представление, что, как выяснилось, намного удобнее и легче осваивается школьниками и взрослыми людьми.

Данный способ позволяет без труда умножать как однозначные числа, так и двузначные, трехзначные и т.д. Разберем подробно геометрический способ умножения чисел.

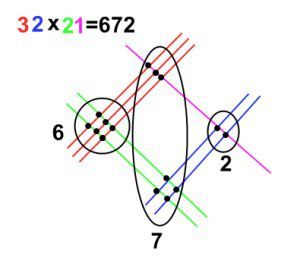
Итак, весь смысл такого умножения заключается в том, что каждую цифру в записи множителей мы представляем графически, т.е. прямыми линиями, количество которых соответствует определенной цифре. Отметим, что линии одного множителя должны пересекать линии другого множителя, а сумма пересечений и есть их произведение.

Рассмотрим геометрический способ на примере. Умножим число 32 на 21 (рис. 2). На листе бумаги поочередно рисуем линии, количество которых определяется из данного примера. Сначала 32: 3 красные линии и чуть ниже - 2 синие. Затем 21: перпендикулярно уже нарисованным, рисуем сначала 2 зеленые, затем – 1 розовую. ВАЖНО: линии первого числа рисуются в направлении из верхнего левого угла в нижний правый, второго числа - из нижнего левого в верхний правый. Затем считаем количество точек пересечения в каждой из трех областей (на рисунке области обозначены в виде окружностей). Итак, в первой области (область сотен) - 6 точек, во второй (область десятков) - 7 точек, в третьей (область единиц) - 2 точки. Следовательно, ответ: 672.

Рис.2

П ример2: умножим 21 на 13. В первом множителе 2 десятка и 1единица, значит строим 2 параллельные прямые и поодаль 1 прямую.

В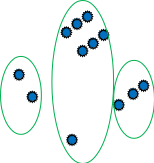 о втором множителе 1 десяток и 3 единицы. Строим параллельно 1 и поодаль 3 прямые, пересекающие прямые первого множителя.

3

2

7

Рис.3

Прямые пересеклись в точках, количество которых и есть ответ, то есть 21 х 13 = 273

Пример 3:24 × 34 = 816

В этом примере есть нюансы. При подсчёте точечек в первой части получилось16. Единичку отправляем-прибавляем к точечкам второй части (20 + 1)…

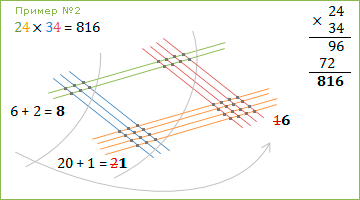
Рис.4

Пример 4: 215 × 741 = 159315

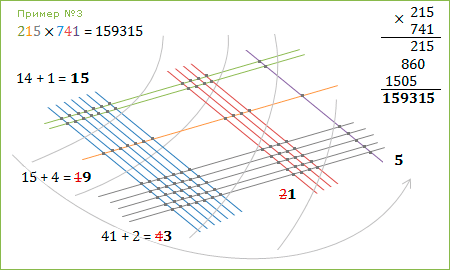
Рис.5

На первых порах рисовательный способ умножения показался мне несколько вычурным, но при этом интригующим и удивительно гармоничным. На пятом примере поймала себя на мысли, что умножение идёт в лёт и работаетв режиме автопилота: рисуем, точечки считаем, про таблицу умножения не вспоминаем, вроде как мы её вообще не знаем (Приложение 1)

Если честно, то осуществляя проверку рисовательного способа умножения и обратившись к умножению столбиком, и не раз, и не два к своему стыду отметила некоторые притормаживания, свидетельствовавшие о том, что таблица умножения у меня проржавела в некоторых местах и забывать её таки не стоит. При работе с более «серьёзными» числами графический способ умножения стал чересчур громоздким, а умножение столбиком пошло в радость.

Забавно и интересно, но проводить 9 прямых при умножении на 9 как-то долго и неинтересно, а потом еще точки пересечения считать… В общем, без таблицы умножения не обойтись!

1. Умножение чисел с «0» в записи числа

В разных источниках информации, где упоминается об умножении чисел графическим способом, я не встречала ни одного примера, где в записи хотя бы одного из множителей присутствует 0, или объяснение того, как умножать такие числа.

Тогда мне пришла идея, как можно графически показать произведение с 0 в записи одного из множителей.

Для начала ознакомимся с принципом умножения чисел в исследуемой ситуации: при умножении двух чисел, в записи которых присутствует 0, геометрическим способом умножения подсчет пересечений линий всех цифр, входящих в запись множителей, с нулем дают 0 пересечений. Справедливость этого правила умножения японским способом с нулем доказана, теперь осталось только проиллюстрировать данное правило.

В подобных примерах умножения с нулем я решила задействовать пунктирные линии как объекты представления нулевых разрядов.

Итак, рассмотрим на примере: умножим 102 на 22. Для начала изобразим число 22 графически (рис. 6). Затем нарисуем 1 линию обозначающую количество сотен, 1 пунктирную линию, обозначающую 0 десятков и 2 линии, обозначающие количество единиц.

4

2 4

2

Рис.6

Таким образом, если не учитывать пересечения с пунктирной линией, то получается верный ответ 2244.

Если же «0» находится в конце числа и обозначает количество единиц, то здесь все решается значительно проще.

Н апример, если нужно перемножить числа 120х35, необходимо перемножить числа 12х35 и в ответе к полученному результату приписать в конце 0. (Рис.7)

3 10

11

Рис.7

Таким образом, 12х35=420, а 120х35=4200

1. Умножение десятичных дробей

Умножение десятичных дробей японским способом также имеет право на существование. Следуя правилу умножения десятичных дробей, представленному в учебнике Н.Я. Виленкина «Математика 5» мы имеем следующую трактовку:  1) числа перемножаются без учета запятых.  
2)   запятая в произведении ставится так, чтобы отделить справа  столько же знаков, сколько отделено в обоих множителях  вместе взятых. 

Таким образом, чтобы выполнить умножение десятичных дробей японским способом нужно выполнить уже привычное нам умножение натуральных чисел, а потом в результате в нужном месте поставить запятую. (Рис.8)

Р ассмотрим пример: 2,6х1,23

18

2

18

10

Рис.8

Таким образом, 26х123=3198, а окончательный ответ 2,6х1,23=3,198

1. Проведение эксперимента

Для проведения эксперимента мы определили группу учащихся 5 класса, состоящую из 15 человек. Мы выбрали учеников с разным уровнем успеваемости, тех у кого по математике «3», «4» и «5».

Объяснив японский способ на разных примерах, мы дали учащимся по 10 примеров: 5 из которых нужно было решить «обычным» столбиком, а 5 оставшихся японским способом. Примеры приведены в Приложении 2.

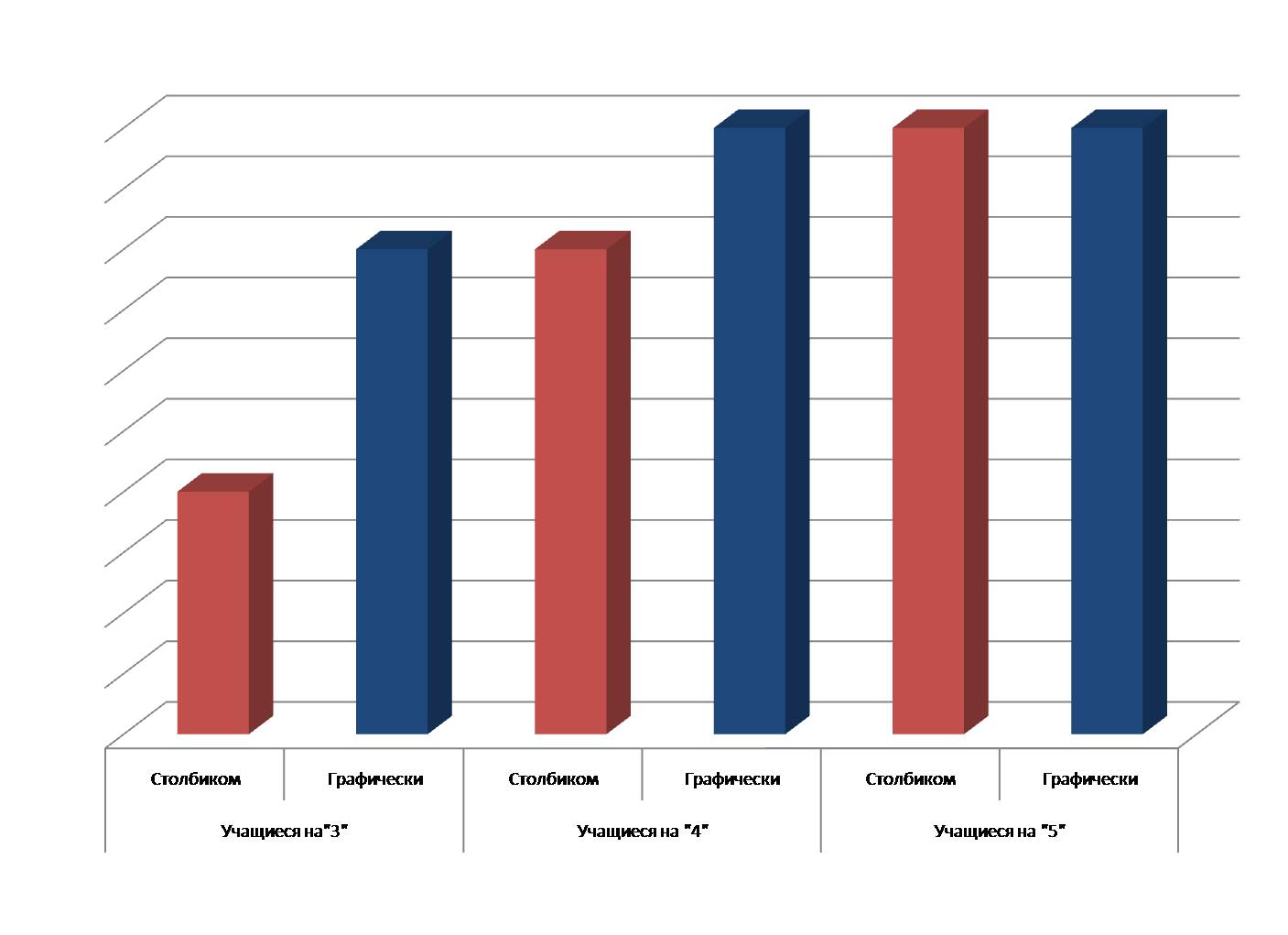
После проведения эксперимента мы проанализировали получившиеся результаты. У тех ребят, у которых стоит оценка «3» в первой группе примеров было по 2-3 ошибки, а во второй группе примеров, которые они решали графическим способом, по 1-2 ошибки. У «хорошистов» было по 1-2 ошибки в первой группе примеров, а во второй группе примеров ошибок вообще не было. У «отличников» не было ошибок ни в первой группе примеров, ни во второй.(Рис.9)

Таким образом, по результатам данного эксперимента можно сделать следующий вывод: японский способ умножения будет полезен тем, у кого есть «проблемы» с таблицей умножения, так как рисовать линии и считать точки пересечения не составляет большого труда.

нет

ошибок

нет

ошибок

нет

ошибок

1-2

ошибки

1-2

ошибки

2-3

ошибки

Рис.9

Заключение

Работая над этой темой мы узнали, что существует забавный и интересный способ умножения, для которого необходимо иметь карандаш, бумагу и пользоваться правилами сложения чисел. Но не для всех примеров этот способ удобен в использовании, особенно при умножении многозначных чисел, состоящих из больших цифр (6,7,8,9) (Приложение 3) . В общем, таблицу умножения все-таки знать нужно!

Узнав этот способ, ребёнок уже в 1-ом классе сможет перемножать любые числа на листе бумаги, при этом процесс будет намного интересней, чем старый способ умножения «столбиком», он будет способствовать развитию эрудиции, вниманию, аккуратности.

Данная работа может быть использована для занятий на математических кружках, дополнительных занятиях с детьми во внеурочное время, как дополнительный материал на уроке по теме «Умножение натуральных чисел». Материал изложен доступно и интересно, что привлечёт внимание и интерес учащихся к предмету математика.

Список литературы

1. Энциклопедия для детей. Т.11. Математика. - М.: Аванта +, 2011

2. http://vasadin.livejournal.com/25290.html

3. https://4brain.ru/schitat-v-ume/_japonskoe-kitajskoe-umnozhenie.php

4. http://iralebedeva.ru/inform7.html

Приложение 1

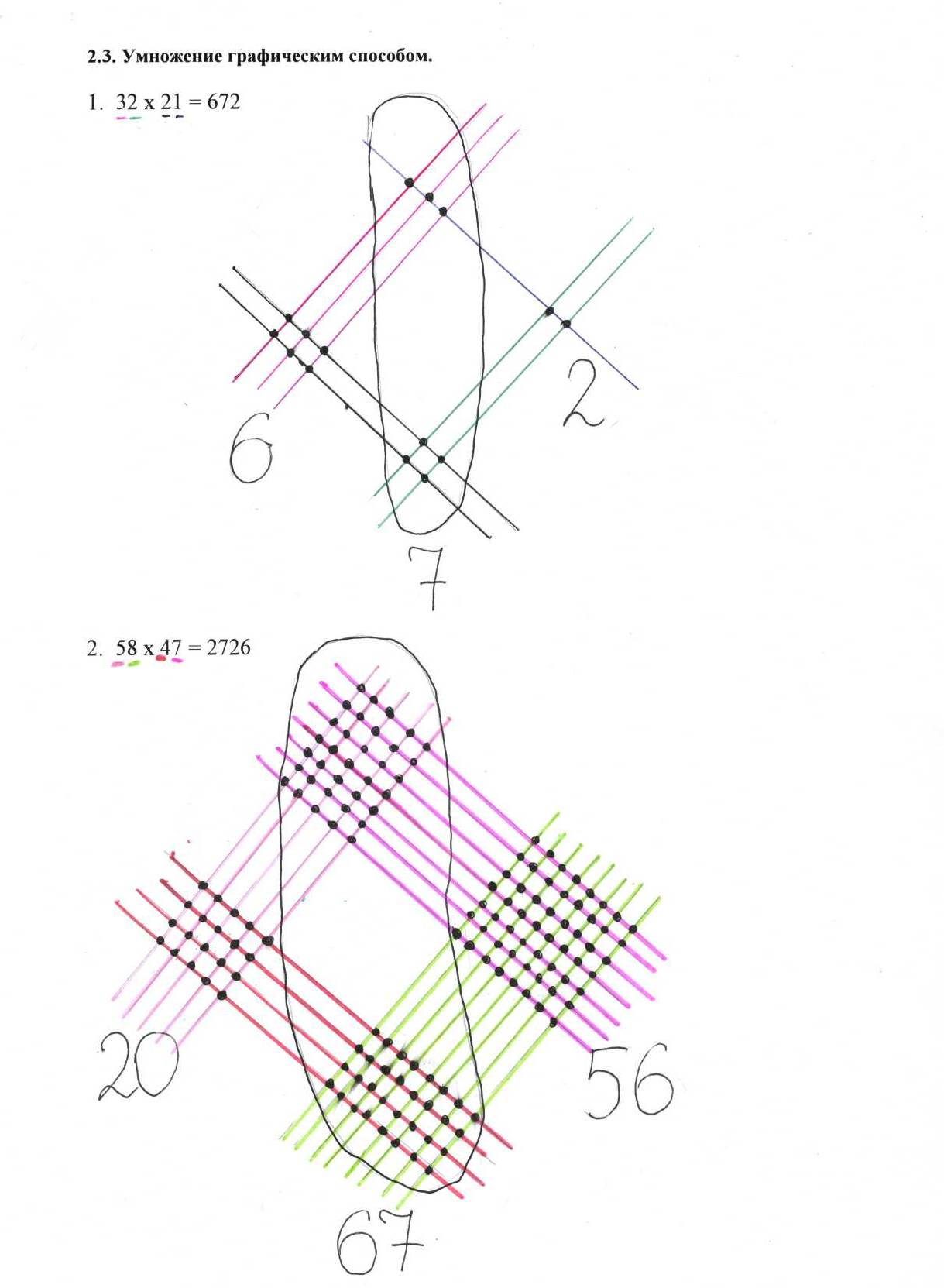
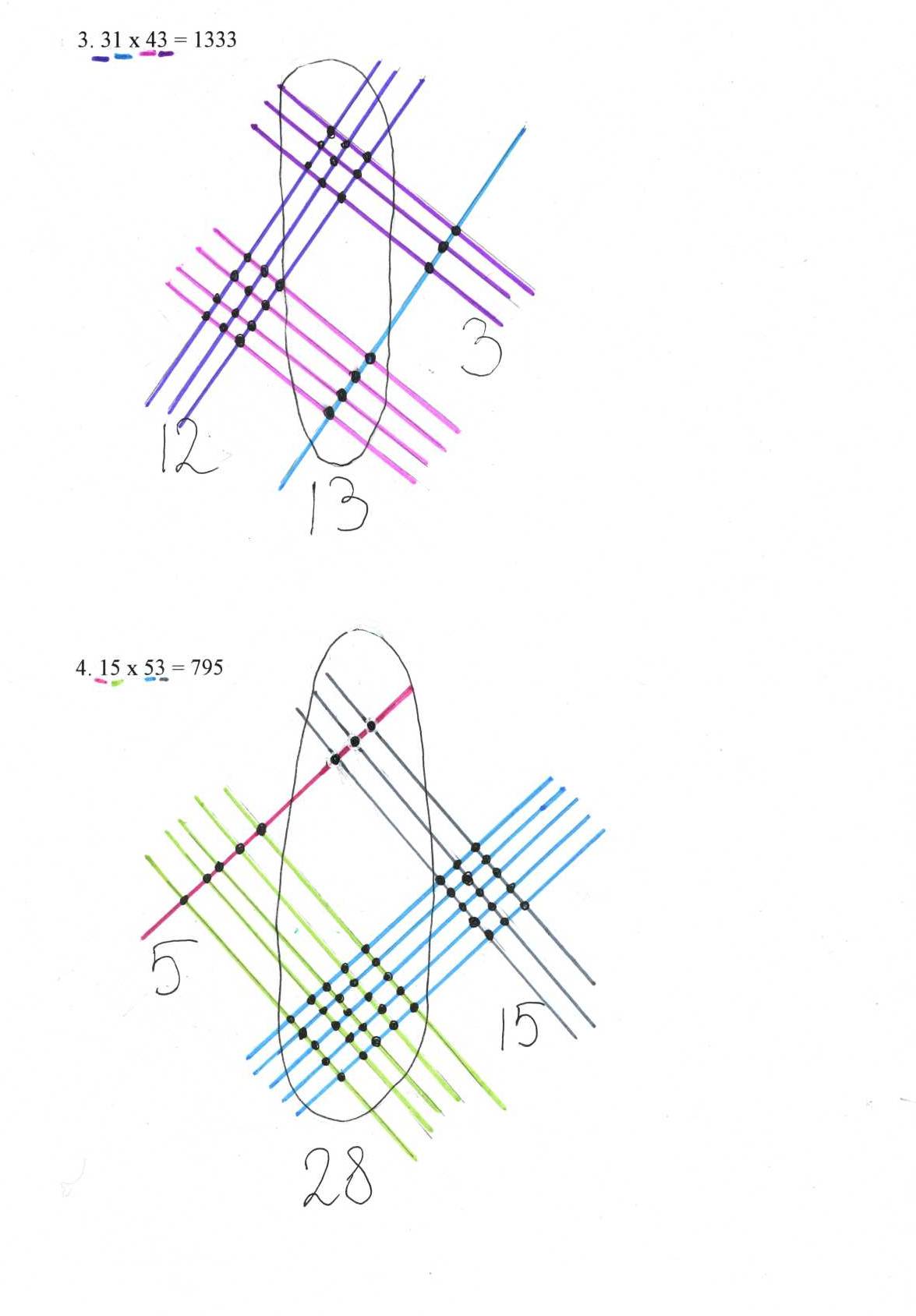
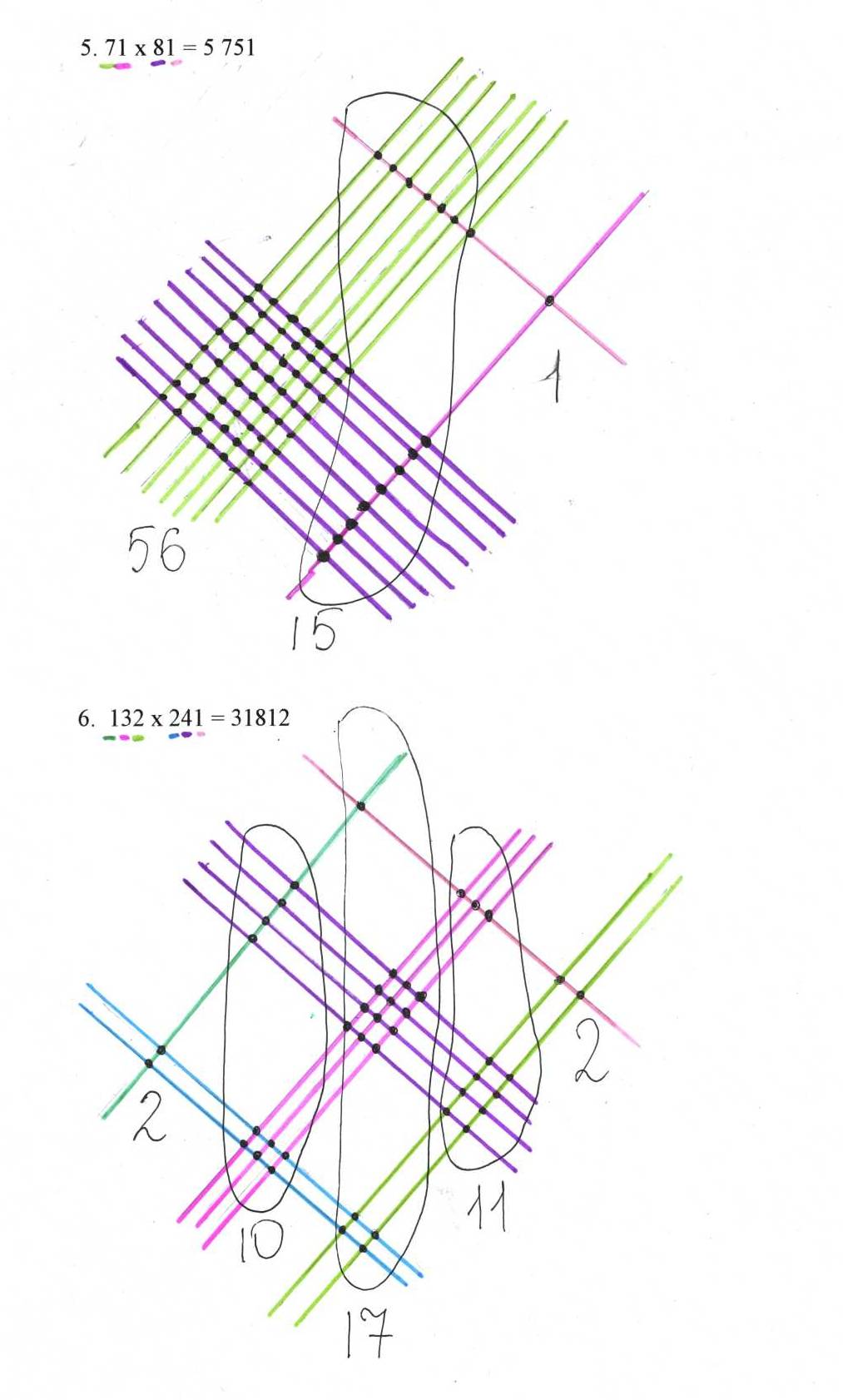
Приложение 2

Примеры для проведения эксперимента

1. Реши примеры столбиком

25х16

124х36

45х134

56х68

325х236

1. Реши примеры графически

23х15

114х42

35х126

53х62

342х254

Приложение 3

Умножение чисел 14759х365421 графическим способом