Муниципальное бюджетное общеобразовательное учреждение
Лицей при ДГТУ №50
Проект:
«Исследование свойств арифметической прогрессии и применение их при решении задач»
г. Миллерово
2022 г.
Содержание
Введение………………………………………………………………….……………
Основная часть
1. Числовые последовательности: история возникновения, основные понятия
1.1 О числовых последовательностях ………………..…………………………….
1.2 Арифметическая прогрессия в древности………………………………..……
2. Арифметическая прогрессия: основные понятия и формулы
2.1 Последовательность … …………………………………………………………
2.2 Арифметическая прогрессия: основные определения……….………………
2.3 Формула n-го члена арифметической прогрессии……………………………
2.4 Исследование арифметической прогрессии…………………………………
2.5 Свойство и признак арифметической прогрессии……………………………
2.6 Сумма первых n членов арифметической прогрессии……………………….
3. Применение числовых последовательностей в различных областях знаний
3.1 Задачи с практическим содержанием из учебников по алгебре…………….
3.2 Арифметическая прогрессия в банковских расчетах, литературе и исторических задачах………………………………………………………………………… ……
Заключение…………………………………………………………………………
Список литературы…………………………………………………………………
«Высшее назначение математики состоит в том,
чтобы находить скрытый порядок в хаосе, который нас окружает»
Винер Н.
Введение
На уроках алгебры 9 класса изучается тема «Арифметическая прогрессия». Важность этой темы школьного курса заключается в ее чрезвычайно широких областях применения, в частности она применяется в заданиях экзамена ОГЭ и ЕГЭ, в задачах банковского содержания. Поэтому мне кажется, важным повторить уже известный из школьного курса материал об арифметической прогрессии и узнать много нового и интересного. Изучая математику внимательнее, мы замечаем, что рано или поздно всякая правильная математическая идея находит применение в том или ином деле. А в каких жизненных ситуациях можно применить знания об арифметической прогрессии и как давно люди знают последовательности, как возникло это понятие? Можно ли увидеть арифметическую прогрессию в природе, экономике и других областях жизни человека? Действительно ли арифметическая прогрессия играют большую роль в повседневной жизни? С учетом этого мною была выбрана тема исследовательской работы: «Исследование свойств арифметической прогрессии и применение их при решении задач»
Проблемный вопрос:
Арифметическая прогрессия – что это?
Имеет ли арифметическая прогрессия практическое применение в повседневной жизни?
Объект исследования: арифметическая прогрессия.
Предмет исследования: исследование свойств арифметической прогрессии и ее практическое применение.
Цель исследования: установить картину возникновения арифметической прогрессии и выявить примеры ее применения.
Задачи исследования:
-
достичь более глубоких знаний по теме Арифметическая прогрессия»;
-
изучить наличие задач на арифметическую прогрессию с практическим содержанием;
-
активизировать интерес к предмету алгебра через поиск и решение как стандартных, так и занимательных задач;
-
формировать умения видеть связь математики с жизнью;
-
найти примеры применения арифметической прогрессий.
Гипотеза исследования: на уроках математики мы много раз слышали о том, что математика – наука очень древняя и возникла она из практических нужд человека. Видимо, и арифметическая прогрессия имеет такие же практические корни, определенное практическое значение.
Методы исследования:
-
Анализ школьных учебников математики, математической справочной литературы, литературы по истории математики, материала из Интернета.
-
Обобщение найденных фактов в учебниках.
Структура исследования:
-
сравнить определения, характеристические свойства арифметической прогрессий;
-
провести анализ исторического экскурса для установления авторства теории о прогрессиях;
-
привести примеры применения прогрессий в различных областях знаний;
Практическая значимость: материалы работы могут использоваться учителями математики на факультативных занятиях в 9 классе.
Основная часть
1.Числовые последовательности: история возникновения, основные понятия
1.1 О числовых последовательностях [2]
В настоящее время числовые последовательности рассматриваются как частные случаи функции. Числовая последовательность есть функция натурального аргумента. (Так, например, арифметическая прогрессия является линейной функцией натурального аргумента). Понятие числовой последовательности возникло и развилось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:
-
1, 2, 3, 4, 5, … - последовательность натуральных чисел.
-
2, 4, 6, 8, 10,… - последовательность чётных чисел.
-
1, 3, 5, 7, 9,… - последовательность нечётных чисел.
-
1, 4, 9, 16, 25,… - последовательность квадратов натуральных чисел.
-
2, 3, 5, 7, 11… - последовательность простых чисел.
Слово прогрессия латинского происхождения (progressio), буквально означает «движение вперёд» (как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VIвв.), первоначально под прогрессией понимали всякую числовую последовательность, построенную по закону, позволяющему неограниченно продолжать её в одном направлении, например последовательность натуральных чисел, их квадратов и кубов. В конце средних веков и в начале нового времени этот термин перестаёт быть общеупотребительным. В XVII веке, например, Дж. Грегори употребляет вместо прогрессии термин «ряд», а другой видный английский математик, Дж. Валлис, применяет для бесконечных рядов термин «бесконечные прогрессии».
В настоящее время мы рассматриваем прогрессии как частные случаи числовых последовательностей.
Возможно, что древние вавилоняне и другие народы той далёкой эпохи имели некоторые общие приёмы решения задач, которые дошли до нас. Однако об этих приёмах мало что известно.
Отдельные случаи суммирования членов прогрессии встречаются в математических памятниках II тысячелетия до н.э. Древние математики не знали общих формул для нахождения членов прогрессии, не было и формул для нахождения сумм ее членов. Однако, известно, что эмпирическим путем в Древнем Египте было выведено (для решения прикладных задач распределения продуктов, деления наследства и т.п.) правило нахождения любого члена арифметической прогрессии, если известны сумма S первых n ее членов и разность прогрессии d. В современных обозначениях правило нахождения первого члена такой прогрессии можно записать в виде формулы 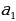 =
=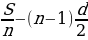 .
.
В V в. до н.э. греки уже знали такие прогрессии, как последовательность натуральных чисел, последовательности четных и нечетных чисел, а также умели находить их суммы:
-
1+2+3+…+n = 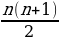 ,
,
-
2+4+6+…+2n = n(n+1),
-
1+3+5+…+(2n-1) = n2 .
Известно, что Архимед исследовал разные последовательности и для нужд механики вывел формулу суммы квадратов натуральных чисел, хотя ею пользовались и до него. 12 + 22 +32 + ... + n2 = 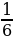 n(n+1)(2n+1).
n(n+1)(2n+1).
Некоторые формулы, относящиеся к прогрессиям, были известны китайским и индийским учёным. Так, Ариабхатта (Vв.) знал формулы для общего члена, суммы арифметической прогрессии и др., Магавира (IXв) пользовался формулой: 12 + 22 +32 + ... + n2 = 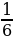 (n+1)(2n+1). Однако правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в «Книге абака» (1202) Леонардо Пизанского. В «Науке о числах» (1484) Н. Шюке, как и Архимед, сопоставляет арифметическую прогрессию с геометрической и даёт общее правило для суммирования любой бесконечно малой убывающей геометрической прогрессии. Формула для суммирования бесконечно убывающей прогрессии была известна П. Ферма и другим математикам XVII века. [1]
(n+1)(2n+1). Однако правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в «Книге абака» (1202) Леонардо Пизанского. В «Науке о числах» (1484) Н. Шюке, как и Архимед, сопоставляет арифметическую прогрессию с геометрической и даёт общее правило для суммирования любой бесконечно малой убывающей геометрической прогрессии. Формула для суммирования бесконечно убывающей прогрессии была известна П. Ферма и другим математикам XVII века. [1]
1.2 Арифметические прогрессии в древности
В клинописных табличках вавилонян, как и в египетских папирусах, относящихся ко II тысячелетию до н.э., встречаются задачи на арифметическую прогрессию.
Вот одна из задач, найденная на вавилонских табличках, в которой используется арифметическая прогрессия.
Задача: «У 10 братьев 1  - мины серебра. Брат над братом поднимается, на сколько поднимается - неизвестно. Доля восьмого 6 шекелей. На сколько выше брат над братом?»
- мины серебра. Брат над братом поднимается, на сколько поднимается - неизвестно. Доля восьмого 6 шекелей. На сколько выше брат над братом?»
Решение:
Итак, 1 мины (мина равна 60 шекелям) серебра, требуется разделить между 10 братьями так, чтобы доли братьев составляли арифметическую прогрессию.
мины (мина равна 60 шекелям) серебра, требуется разделить между 10 братьями так, чтобы доли братьев составляли арифметическую прогрессию.
Требуется найти разность прогрессии, зная, что восьмой брат получает 6 шекелей.
(В Древнем Вавилоне ученые не знали формул, а каждый раз решали задачи арифметическими методами.)
1 способ: Вавилонский автор, не имевший в своем распоряжении ни современной символики, ни готовых формул, вынужден придерживаться строго арифметических рассуждений. Идея его решения следующая.
Найдем среднюю для всех долю: 100 : 10= 10 (шекелей). Удвоенная средняя доля (т.е. 20 шекелей) – это сумма долей третьего и восьмого братьев (имея в виду, что первого от третьего, как и восьмого от десятого отделяют 2 ступени, две разности). Если у восьмого брата 6 шекелей, то у третьего 20 – 6 = 14 (шекелей). Разность между их долями составляет 14 – 6 = 8 (шекелей). Третьего брата от восьмого отделяют 5 ступеней, значит, одна ступень равна 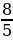 шекеля.
шекеля.
Замечание: в задаче речь шла об арифметической прогрессии, члены которой уменьшаются, т.е. у этой прогрессии 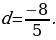
2 способ: Здесь требуется по сумме первых 10 членов арифметической прогрессии 5/3 мины (1 мина = 60 шекелей) и известному 8-му члену определить разность арифметической прогрессии:
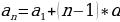 ,
,
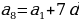 ,
, 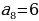 ,
,
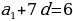 ,
, 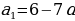 ;
;
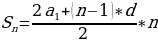
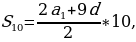
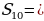 1
1  мины = (
мины = (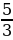 * 60) шекелей = 100 шекелей
* 60) шекелей = 100 шекелей
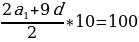 ,
, 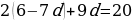 , 12 - 14
, 12 - 14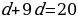 , -5
, -5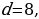
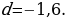
Ответ. На 1,6 шекелей брат выше брата.
А вот египетская задача из папируса Ахмеса.
Задача: «Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками, разность же между каждым человеком и его соседом равна 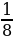 меры».
меры».
При решении этой и других аналогичных задач египтяне, видимо, пользовались правилом, которое можно записать в современной символике так:
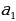 =
=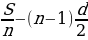 .
.
Оно эквивалентно нашей формуле 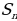 =
= 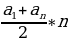
Происхождение этого правила не установлено: оно, вероятно, эмпирического характера.
Древнейшая задача на прогрессию – не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой двухтысячелетнюю давность, а гораздо более старая задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом в конце 19 века, составлен около 2000 лет до нашей эры и является списком с другого, ещё более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры. В числе арифметических, алгебраических, геометрических задач этого документа имеется такая:
« Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго и пятый больше четвёртого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому?»
Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго и пятый больше четвёртого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому?»
РЕШЕНИЕ.
Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый член х, разность у. Тогда:
Доля первого………………………………х
Доля второго………………………………х+у
Доля третьего……………………………..х+2у
Доля четвёртого………………………….х+3у
Доля пятого…………………………………х+4у
На основании условий задачи составляем следующие два уравнения:
х+(х+у)+(х+2у)=(х+3у)+(х+4у)=100
7(х+(х+у))=(х+2у)=(х+3у)+(х+4у).
После упрощений получаем: х+2у=20
11х=2у
Решив эту систему, получаем: Х=1 2/3, У=9 1/6
Значит, хлеб должен быть разделён на следующие части:
1 2/3, 10 5/6, 20, 29 1/6, 38 1/3.
Задачи на арифметические (и геометрические) прогрессии имеются и в древнекитайском тракте «Математика в девяти книгах», в котором нет, однако, указаний на применение какой-либо формулы суммирования.
Первые из дошедших до нас задач на прогрессии связаны с запросами хозяйственной жизни и общественной практики, как, например, распределение продуктов, деление наследства и т.д.
2.Арифметическая прогрессия
Арифметическая прогрессия — это специального вида последовательность. Поэтому прежде чем давать определение арифметической прогрессии, нам нужно вкратце обсудить важное понятие числовой последовательности.
2.1 Последовательность
Вообразите устройство, на экране которого высвечиваются одно за другим некоторые числа. Скажем, 2, — 7,13,1, -6, 0, 3,... Такой набор чисел как раз и является примером последовательности.
Определение. Числовая последовательность — это множество чисел, в котором каждому числу можно присвоить уникальный номер (то есть поставить в соответствие единственное натуральное число)1. Число с номером n называется n-м членом последовательности.
Так, в приведённом выше примере первый номер имеет число 2 — это первый член последовательности, который можно обозначить а1; номер пять имеет число —6 — это пятый член последовательности, который можно обозначить а5. Вообще, n-й член последовательности обозначается аn (или bn, cn и т.д.).
Очень удобна ситуация, когда n-й член последовательности можно задать некоторой формулой. Например, формула ап = 2n — 3 задаёт последовательность: —1,1, 3,5, 7,... Формула ап = (—1)n задаёт последовательность: —1,1, —1,1,...
Не всякое множество чисел является последовательностью. Так, отрезок [0; 1] — не последовательность; в нём содержится «слишком много» чисел, чтобы их можно было перенумеровать. Множество R всех действительных чисел также не является последовательностью. Эти факты доказываются в курсе математического анализа.
2.2 Арифметическая прогрессия: основные определения
ОПРЕДЕЛЕНИЕ. Арифметическая прогрессия — это последовательность, каждый член которой, начиная со второго равен предыдущему, сложенному с одним и тем же числом (разностью арифметической прогрессии).
Например, последовательность 2, 5,8,11,... является арифметической прогрессией с первым членом 2 и разностью 3. Последовательность 7, 2, —3, —8,... является арифметической прогрессией с первым членом 7 и разностью —5. Последовательность 3, 3, 3,... является арифметической прогрессией с разностью, равной нулю.
Эквивалентное определение: последовательность ап называется арифметической прогрессией, если разность аn+1 — аn есть величина постоянная (не зависящая от n).
Арифметическая прогрессия называется возрастающей, если её разность положительна, и убывающей, если её разность отрицательна.
2.3 Формула n-го члена арифметической прогрессии
Легко понять, что арифметическая прогрессия полностью определяется двумя числами: первым членом и разностью. Поэтому возникает вопрос: как, зная первый член и разность, найти произвольный член арифметической прогрессии?
Получить искомую формулу n-го члена арифметической прогрессии нетрудно. Пусть аn — арифметическая прогрессия с разностью d. Имеем:
аn+1 = аn + d (n = 1, 2,...).
В частности, пишем:
а2 = а1 + d,
а3 = а2 + d = (а1 + d) + d = а1 + 2d,
а4 = а3 + d = (а1 + 2d) + d = а1 + 3d,
и теперь становится ясно, что формула для аn имеет вид:
аn = а1 + (n — 1)d. (1)
Задача 1. В арифметической прогрессии 2, 5, 8,11,... найти формулу n-го члена и вычислить сотый член.
Решение. Согласно формуле (1) имеем:
an = 2 + 3(n — 1) = 3n — 1.
Отсюда
а100 = 3 * 100 — 1 = 299.
2.4 Исследование арифметической прогрессии
Из формулы n-го члена арифметической прогрессии следует, что
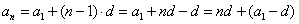 . Это означает, что арифметическая прогрессия зависит от n, т.е. является функцией натурального аргумента.
. Это означает, что арифметическая прогрессия зависит от n, т.е. является функцией натурального аргумента.
Вывод: арифметическая прогрессия – это линейная функция натурального аргумента
y = dx + m, где m = a1 – d, x 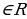 .
.
Если d 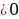 , то линейная функция возрастает и арифметическая прогрессия (an) - возрастающая;
, то линейная функция возрастает и арифметическая прогрессия (an) - возрастающая;
если d 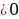 , то линейная функция убывает и арифметическая прогрессия (an) - убывающая.
, то линейная функция убывает и арифметическая прогрессия (an) - убывающая.
Пример 1.
Дано: (an)- арифметическая прогрессия, (an) =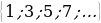 .
.
Найти: формулу n-го члена арифметической прогрессии an.
Доказать: (an) - возрастающая.
Дать: геометрическую иллюстрацию.
Решение.
a1 = 1, a2 = 3, d = a2 – a1 = 3 – 1 = 2.
Тогда аn = а1 + (n — 1)d, an =1 + (n — 1)*2 = 1 + 2n – 2 = 2n –1,
т.е. an = 2n –1.
Поскольку d = 2 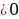 , заданная арифметическая прогрессия – возрастающая.
, заданная арифметическая прогрессия – возрастающая.
Ч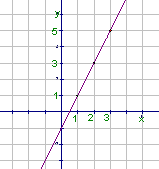 тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 2x - 1 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 1).
тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 2x - 1 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 1).
Рис. 1. График функции y = 2x – 1.
Пример 2.
Дано: (an)- арифметическая прогрессия, (an) =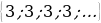 .
.
Найти: формулу n-го члена арифметической прогрессии an.
Дать: геометрическую иллюстрацию.
Решение.
a1 = 3, a2 = 3, d = a2 – a1 = 3 – 3 = 0 .
Тогда an = 3 для любого натурального числа.
Ч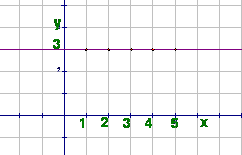 тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 3 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 2).
тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 3 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 2).
Рис. 2. График функции y = 3.
Пример 3.
Дано: (an)- арифметическая прогрессия, (an) =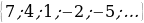 .
.
Найти: формулу n-го члена арифметической прогрессии an.
Доказать: (an) - убывающая.
Дать: геометрическую иллюстрацию.
Решение.
a1 = 7, a2 = 4, d = a2 – a1 = 4 – 7 = -3.
Тогда аn = а1 + (n — 1)d, an =7 + (n — 1)*(-3)= 7 - 3n + 3 = -3n + 10,
т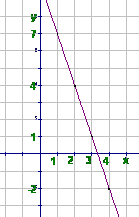 .е. an = -3n +10.
.е. an = -3n +10.
Поскольку d 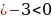 , заданная арифметическая прогрессия – убывающая.
, заданная арифметическая прогрессия – убывающая.
Чтобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = -3x + 10 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 3).
Рис. 3. График функции y = -3x + 10.
2.5 Свойство и признак арифметической прогрессии
Свойство АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ. В арифметической прогрессии аn для любого n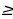 2 выполнено равенство
2 выполнено равенство
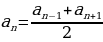 (2)
(2)
Иначе говоря, каждый член арифметической прогрессии (начиная со второго) является средним арифметическим соседних членов.
Доказательство. Имеем:
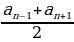 =
= 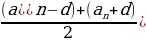 =
= 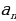 ,
,
что и требовалось.
Более общим образом, для арифметической прогрессии ап справедливо равенство
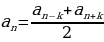
при любом n 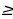 2 и любом натуральном k n.
2 и любом натуральном k n.
Оказывается, формула (2) служит не только необходимым, но и достаточным условием того, что последовательность является арифметической прогрессией.
Признак арифметической прогрессии. Если для всех n 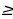 2 выполнено равенство (2), то последовательность ап является арифметической прогрессией.
2 выполнено равенство (2), то последовательность ап является арифметической прогрессией.
Доказательство. Перепишем формулу (2) следующим образом:
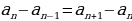 .
.
Отсюда видно, что разность 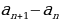 не зависит от n, а это как раз и означает, что последовательность
не зависит от n, а это как раз и означает, что последовательность 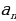 есть арифметическая прогрессия.
есть арифметическая прогрессия.
Свойство и признак арифметической прогрессии можно сформулировать в виде одного утверждения; мы для удобства сделаем это для трёх чисел (именно такая ситуация часто встречается в задачах).
Характеризация арифметической прогрессии. Три числа а, b, с образуют арифметическую прогрессию тогда и только тогда, когда 2b = а + с.
Задача 2. (МГУ, экономич. ф-т, 2007) Три числа 8x, 3—x2 и —4 в указанном порядке образуют убывающую арифметическую прогрессию. Найдите x и укажите разность этой прогрессии.
Решение. По свойству арифметической прогрессии имеем:
2(3 — x2) = 8x — 4  2x2 + 8x — 10 = 0
2x2 + 8x — 10 = 0 x2 + 4x — 5 = 0
x2 + 4x — 5 = 0  x =1, x = —5.
x =1, x = —5.
Если x = 1, то получается убывающая прогрессия 8, 2, —4 с разностью —6. Если x = —5, то получается возрастающая прогрессия —40, —22, —4; этот случай не годится.
Ответ: x =1, разность равна —6.
2.6 Сумма первых n членов арифметической прогрессии
Легенда гласит, что однажды учитель велел детям найти сумму чисел от 1 до 100 и сел спокойно читать газету. Однако не прошло и нескольких минут, как один мальчик сказал, что решил задачу. Это был 9-летний Карл Фридрих Гаусс, впоследствии один из величайших математиков в истории.
Идея маленького Гаусса была такова. Пусть
S =1 + 2 + 3 + ... + 98 + 99 + 100.
Запишем данную сумму в обратном порядке:
S = 100 + 99 + 98 + ... + 3 + 2 + 1,
и сложим две этих формулы:
2S = (1 + 100) + (2 + 99) + (3 + 98) + ... + (98 + 3) + (99 + 2) + (100 + 1). Каждое слагаемое в скобках равно 101, а всего таких слагаемых 100. Поэтому
2S = 101 * 100 = 10100,
откуда
S = 5050.
Мы используем эту идею для вывода формулы суммы
S = а1 + а2 + ... + аn
первых n членов арифметической прогрессии. Именно, запишем друг под другом:
S = a1 + a 2 + a3 + ... + аn-2 + an-1 + an,
S = an + an-1 + an-2 + ... + a3 + a2 + a1
и сложим:
2S =(a1 + an)+(a2 + an-1) + (a3 + an-2) +...+(an-2 + a 3) + (an-1 + a2) + (an+a1). Каждое слагаемое в скобках равно a1 + an, а всего таких слагаемых n.
Поэтому
2S = (a1 + an)*n,
Откуда
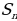 =
= 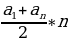 . (3)
. (3)
Полезная модификация формулы (3) получается, если в неё подставить формулу n-го члена an = a1 + (n — 1)d:
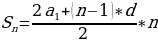 . (4)
. (4)
Задача. Найти сумму всех положительных трёхзначных чисел, делящихся на 13.
Решение. Трёхзначные числа, кратные 13, образуют арифметическую прогрессию с первым членом 104 и разностью 13; n-й член этой прогрессии имеет вид:
an = 104 + 13(n — 1) = 91 + 13n.
Давайте выясним, сколько членов содержит наша прогрессия. Для этого решим неравенство:
an 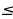 999,
999,
91 + 13n 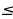 999,
999,
13n 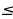 908,
908,
n 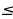
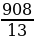 ,
,
n 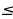
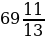 ,
,
n 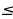
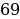 .
.
Итак, в нашей прогрессии 69 членов. По формуле (4) находим искомую сумму:
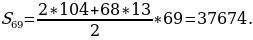
Ответ: 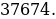
3. Применение арифметической прогрессии в разных областях знаний
3.1 Задачи с практическим содержанием из учебников по алгебре
Задача №1
«В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?»
Решение:
Составим математическую модель задачи. Система штрафных очков составляет арифметическую прогрессию, первый член которой равен 1, а разность – 0,5.Сумма первых n членов (количество промахов) – 7. Найдем число промахов:
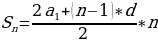
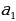 =1,
=1, 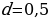 ,
, 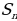 = 7,
= 7, 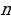 - ?
- ?
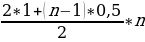 = 7,
= 7,
(2 + 0,5n – 0,5)*n = 14,
(1,5+ 0,5n)*n = 14,
1,5n + 0,5n2 – 14 = 0,
n2 + 3n – 28 = 0,
n1= - 7, n2= 4,
n 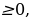 n = 4
n = 4
Т.о., число промахов 4, в цель стрелок попал 25 – 4 = 21 раз.
Ответ. Число промахов 4, в цель стрелок попал 21 раз.
Задача №2
«Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?» 
Решение:
Составим математическую модель задачи:
5, 10, 15,…,40, 40, 40, 35, 30,…,5
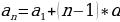 ,
,
40 = 5+ (n-1)*5,
n=8;
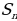 =
= 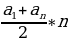 ,
,
S8 = 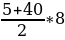 =180, 180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.
=180, 180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.
Ответ: 2.
Задача №3
«Улитка ползет по дереву. За первую минуту она проползла 30 см, а за каждую следующую минуту — на 5 см больше, чем за предыдущую. За какое время достигнет улитка вершины дерева длиной 5,25 м, если считать, что движение начато от его основания?»
Решение:
5,25 м= 525 см
a1 =30, d=5, Sn= 525, n 0.
0.
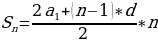 ;
;
525= 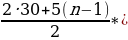 n,
n,
1050= (60+ 5 (n-1))n;
1050= 55 n + 5n2;
n2 +11 n -210=0,
n1=-21, n2=10 (n 0). Улика достигнет вершины за 10 дней.
0). Улика достигнет вершины за 10 дней.
Ответ: за10 дней.
Задача №4
« Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходи ли на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000 м?»
Решение:
Составим математическую модель задачи:
1400, 1300, …, 1400-100(n-1).
a1=1400; d= -100, Sn=5000. Надо найти n.
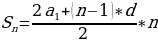
5000= 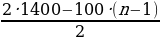 *n,
*n,
10000= (2800-100 n+100) n,
10000= (2900-100 n) n;
100 n2-2900 n+10000=0,
n2-29 n+100=0,
n1=25, n2=4.
Условию задачи удовлетворяет n=4 ( при n=25 аn=-1000). Значит, альпинисты покорили высоту за 4 дня.
Ответ: за 4 дня.
Задача №5
«За изготовление и установку самого нижнего железобетонного кольца колодца заплатили 26 условных единиц (у. в.), а за каждое следующее кольцо платили на 2 у. е. меньше, чем за предыдущее. Кроме того, по окончании работы было уплачено ещё 40 у. е. Средняя стоимость изготовления и установки кольца оказалась равной 22 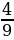 у. е. Сколько колец было установлено?»
у. е. Сколько колец было установлено?»
Эта задача из решебника всех конкурсных задач по математике сборника под редакцией М. И. Сканави.
Решение:
Так как за установку первого кольца заплатили 26 рублей, а за каждое следующее на 2 рубля меньше, то имеет место арифметическая прогрессия: а1=26, d=-2, n – количество членов (колец).
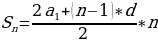
 Чтобы найти среднюю стоимость установки одного кольца нужно к этой сумме прибавить 40 рублей и результат разделить на n. Таким образом, получим уравнение относительно переменной n:
Чтобы найти среднюю стоимость установки одного кольца нужно к этой сумме прибавить 40 рублей и результат разделить на n. Таким образом, получим уравнение относительно переменной n:
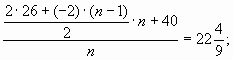
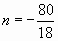
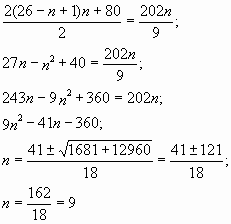
Очевидно, что количество колец не может быть отрицательным.
Таким образом, было установлено 9 колец.
Ответ: 9 колец.
Задача №6
«При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько брёвен находится в одной кладке, если в ее основании положено 12 бревен?»
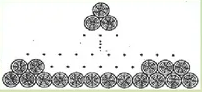
Решение:
1, 2, 3, 4,…,12. Это арифметическая прогрессия: а1=1, d=1, аn=12. Надо найти n.
аn=a1+d(n-1); 12=1+1(n-1); n=12.
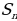 =
= 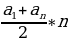 ;
;
Sn =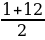 ·12 =78.
·12 =78.
В одной кладке находится 78 бревен.
Ответ: 78 бревен.
3.2 Арифметическая прогрессия в банковских расчетах, литературе и исторических задачах
Арифметическая прогрессия и банковские расчеты
Представьте себе, что вы открыли в банке вклад в сумме а р. под р% годовых на t лет. Вы хотите в конце каждого года хранения вклада снимать проценты по вкладу, т.е. полученную прибыль в размере p% . Какой доход вы получите?
При t = 1 вы получите (а +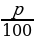 *a )р.,
*a )р.,
при t = 2 ваша итоговая сумма составит (а + 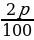 *a)р.,
*a)р.,
и т. д. Математическая модель ситуации — конечная арифметическая прогрессия
а, а +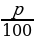 *a, а +
*a, а + 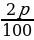 *a, …, а +
*a, …, а + 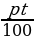 *a.
*a.
Итак, за t лет вы получите
а(1 +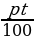 )— это так называемая формула простых процентов.
)— это так называемая формула простых процентов.
Арифметическая прогрессия в литературе
«…Не мог он ямба от хорея
Как мы не бились отличить…».
Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха.
Ямб – это стихотворный размер с ударением на четных слогах 2; 4; 6; 8;…Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.
Хорей – это стихотворный размер с ударением на нечетные слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7;..
Примеры.
Ямб. «Мой дЯдя сАмых чЕстных прАвил…»\ Маяковский, прогрессия 2; 4; 6; 8;…
Хорей. «Я пропАл, как звЕрь в загОне»\Б.Л.Пастернак, «БУря мглОю нЕбо крОет»\ А.С. Пушкин, прогрессия 1; 3; 5;7;
Задачи из «Арифметики» Л.Ф.Магницкого
Купец имел 14 чарок серебряных, причем веса чарок растут по арифметической прогрессии с разностью 4. Последняя чарка весит 59 латов. Определить, сколько весят все чарки.
Решение
а14=а1+13d, a1=59-13·4=7, S14= 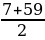 ·14=462.
·14=462.
Ответ: все чарки весят 462 лата.
Задача
Два тела движутся навстречу одно другому из двух мест, находящихся в расстоянии 153 футов. Первое проходит по 10 футов в секунду, а второе в первую секунду прошло 3 фута и в каждую следующую секунду проходит 5-ю футами больше, чем в предыдущую. Через сколько секунд тела встретятся?
Решение:
Второе тело пройдет за n сек
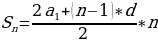
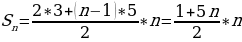 (фут), а первое тело - 10n фут,
(фут), а первое тело - 10n фут,
(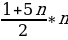 + 10n) фут – расстояние между телами в начальный момент, по условию оно равно 153 футам.
+ 10n) фут – расстояние между телами в начальный момент, по условию оно равно 153 футам.
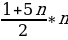 + 10n =153,
+ 10n =153,
n=6, n=-10,2. Так как n 0, то n=6.
0, то n=6.
Значит, тела встретятся через 6 секунд.
Ответ: тела встретятся через 6 секунд.
Заключение
В ходе выполнения данного исследования я установил, что сами по себе прогрессии известны так давно, что нельзя говорить о том, кто их открыл. Убедился в том, что задачи на прогрессии, дошедшие до нас из древности, также как и многие другие знания по математике, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и др. Выяснил, что в развитие теории о прогрессиях большой вклад внесли: Архимед, Пифагор и его ученики, французский математик Леонард Фибоначчи. Нашел много задач на арифметическую прогрессию в старых и в современных учебниках по математике. Сделав анализ задач на прогрессии с практическим содержанием, увидел, что арифметическая прогрессия встречается в банковских расчетах литературе и других жизненных ситуациях, следовательно, нам необходим навык применения знаний, связанных с арифметической прогрессией.
Таким образом, поставленная цель проекта установить картину возникновения понятия прогрессии; выявление интересных фактов об арифметической прогрессии; применение в жизненных ситуациях достигнута, проблема решена.
Литература и сайты Интернета:
-
Аксенова М.Д. Энциклопедия для детей Т.11. Математика гл. ред. Аксенова М.Д. – М.: Аванта «+», 1998.
-
Глейзер Г. И. История математики в школе 7 – 8 классы.–М.: Просвещение, 1982.
-
Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин.Алгебра. 9 класс: учебник для общеобразовательных организаций/ -М.: Просвещение, 2017.
-
Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б. Алгебра. 9 класс,
Учебник для общеобразовательных учреждений -М.: Просвещение, 2009,
-
Мордкович А.Г., П.В. Семенов , Алгебра. 9 класс, в 2ч. Ч.2. Учебник для общеобразовательных учреждений -М.: Мнемозина, 2010.
-
Савин А.П. Энциклопедический словарь юного математика.-М.: Педагогика, 1989
-
http://www.goldenmuseum.com/0206Rabbit_rus.html
-
http://leon-orr.livejournal.com/1237766.html
-
http://infourok.ru/urok-s-prezentaciey-po-matematike-na-temu-arifmeticheskaya-i-geometricheskaya-progressiya-448288.html
-
http://festival.1september.ru/articles/602556/pril3.ppt
1






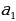 =
=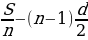 .
.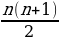 ,
,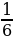 n(n+1)(2n+1).
n(n+1)(2n+1). - мины серебра. Брат над братом поднимается, на сколько поднимается - неизвестно. Доля восьмого 6 шекелей. На сколько выше брат над братом?»
- мины серебра. Брат над братом поднимается, на сколько поднимается - неизвестно. Доля восьмого 6 шекелей. На сколько выше брат над братом?»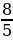 шекеля.
шекеля.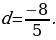
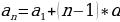 ,
,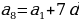 ,
, 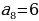 ,
,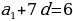 ,
, 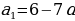 ;
;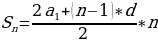
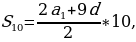
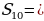 1
1 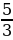 * 60) шекелей = 100 шекелей
* 60) шекелей = 100 шекелей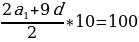 ,
, 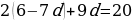 , 12 - 14
, 12 - 14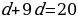 , -5
, -5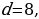
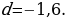
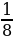 меры».
меры». 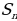 =
= 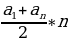
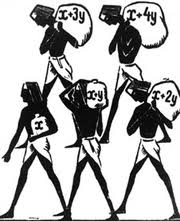 Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго и пятый больше четвёртого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому?»
Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго и пятый больше четвёртого. Кроме того, двое первых должны получить в 7 раз меньше трёх остальных. Сколько нужно дать каждому?»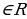 .
.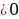 , то линейная функция возрастает и арифметическая прогрессия (an) - возрастающая;
, то линейная функция возрастает и арифметическая прогрессия (an) - возрастающая;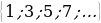 .
. тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 2x - 1 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 1).
тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 2x - 1 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 1).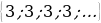 .
. тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 3 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 2).
тобы дать геометрическую иллюстрацию данной арифметической прогрессии, нужно построить график линейной функции y = 3 и отметить точки с абсциссами, равными 1,2,3,4,…(см. Рис. 2).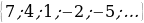 .
. .е. an = -3n +10.
.е. an = -3n +10.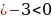 , заданная арифметическая прогрессия – убывающая.
, заданная арифметическая прогрессия – убывающая.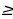 2 выполнено равенство
2 выполнено равенство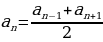 (2)
(2)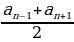 =
= 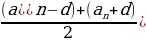 =
= 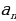 ,
,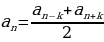
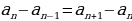 .
.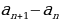 не зависит от n, а это как раз и означает, что последовательность
не зависит от n, а это как раз и означает, что последовательность  2x2 + 8x — 10 = 0
2x2 + 8x — 10 = 0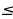 999,
999, 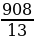 ,
,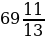 ,
,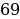 .
.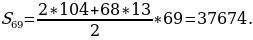
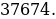
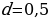 ,
, 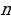 - ?
- ?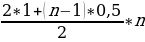 = 7,
= 7, 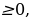 n = 4
n = 4
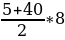 =180, 180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.
=180, 180 капель больной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства. 0.
0.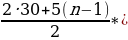 n,
n, 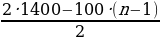 *n,
*n, 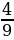 у. е. Сколько колец было установлено?»
у. е. Сколько колец было установлено?»  Чтобы найти среднюю стоимость установки одного кольца нужно к этой сумме прибавить 40 рублей и результат разделить на n. Таким образом, получим уравнение относительно переменной n:
Чтобы найти среднюю стоимость установки одного кольца нужно к этой сумме прибавить 40 рублей и результат разделить на n. Таким образом, получим уравнение относительно переменной n: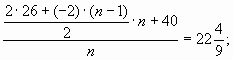
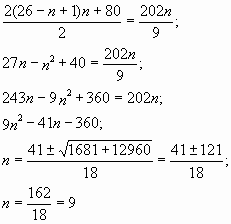

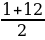 ·12 =78.
·12 =78.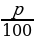 *a )р.,
*a )р., 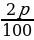 *a)р.,
*a)р., 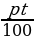 *a.
*a.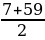 ·14=462.
·14=462.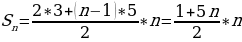 (фут), а первое тело - 10n фут,
(фут), а первое тело - 10n фут,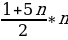 + 10n) фут – расстояние между телами в начальный момент, по условию оно равно 153 футам.
+ 10n) фут – расстояние между телами в начальный момент, по условию оно равно 153 футам.


















