Россия, Алейск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 06.09.2025 07:53
Проказова Ольга Владимировна
учитель математики и информатики
58 лет
2 497
24 937 
Местоположение
Специализация
Исследовательский проект "Решение квадратных уравнений"
Категория:
Математика
01.03.2020 14:02
Просмотр содержимого документа
«Исследовательский проект "Решение квадратных уравнений"»
Муниципальное бюджетное общеобразовательное учреждение «Школа № 13»
ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ ПО
МАТЕМАТИКЕ
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ
автор проекта:
ученица 8 класса
Лиханова Карина
руководитель:
учитель математики
и информатики
Проказова О.В.
Рубцовск,2020
«Ур a внение - эт o з o л o т o й ключ, открыв a ющий вс e м a т e м a тич e ски e с e з a мы.» С. К o в a ль
Актуальность:
современные научно-методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Цель работы:
разработать методическое пособие для учащихся, содержащее различные способы решения квадратных уравнений, выделить эффективные способы решения и показать их практическое применение.
Задачи:
Гипотеза: любое квадратное уравнение можно решить всеми существующими способами.
Объект исследования: квадратные уравнения .
Предмет исследования: способы решения уравнений второй степени .
Методы исследования:
теоретический, математический, графический.
Впервые я услышала о квадратных уравнениях на уроках алгебры от учителя. Особенно меня заинтересовали способы их решения, причем наиболее рациональные.
Во-первых , удивило сочетание слов « квадратное », « уравнение ».
Во-вторых , чем знамениты эти уравнения.
В-третьих , почему их решением так долго занимались великие ученые.
В-четвертых , способы решения квадратных уравнений и их практическая значимость.
Определение квадратного уравнения, его виды:
Квадратным уравнением называется уравнение вида ax2 +bx + c = 0,
где х - переменная,
а,b,с – некоторые числа, причем, а ≠ 0.
Если в квадратном уравнении хотя бы один из коэффициентов b или с равен нулю , то такое уравнение называют
неполным квадратным уравнением.
Неполные квадратные уравнения бывают трёх видов: 1) ах2 + с = 0, где с ≠ 0; 2) ах2 + bх = 0, где b ≠ 0; 3) ах2 = 0.
Немного из истории:
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств.
- Квадратные уравнения в Древнем Вавилоне;
- Квадратные уравнения в Индии;
- Квадратные уравнения у ал-Хорезми;
- Квадратные уравнения в Европе Х III- XVII вв.
Разложение левой части уравнения на множители:
Пример:
Метод выделения полного квадрата (классический метод).
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 8х -9= х 2 + 2• х • 4-9 .
Преобразуем теперь левую часть уравнения
прибавляя к ней и вычитая 4 2 . Имеем:
Таким образом, данное уравнение можно записать так:
Решение квадратных уравнений по формуле с четным коэффициентом.
Пример:
0 и p = - 3 x 2 + 8 x + 7 = 0; x 1 = - 7 и x 2 = - 1, так как q = 7 0 и p = 8 0 . Теорема Виета. Б) x 2 + 4 x – 5 = 0; x 1 = - 5 и x 2 = 1, так как q = - 5 и p = 4 0; x 2 – 8 x – 9 = 0; x 1 = 9 и x 2 = - 1, так как q = - 9 и p = - 8 " width="640"
А) x 2 – 3 x + 2 = 0; x 1 = 2 и x 2 = 1,
так как q = 2 0 и p = - 3
x 2 + 8 x + 7 = 0; x 1 = - 7 и x 2 = - 1,
так как q = 7 0 и p = 8 0 .
Теорема Виета.
Б) x 2 + 4 x – 5 = 0; x 1 = - 5 и x 2 = 1,
так как q = - 5 и p = 4 0;
x 2 – 8 x – 9 = 0; x 1 = 9 и x 2 = - 1,
так как q = - 9 и p = - 8
Решение уравнений способом «переброски»
квадратное уравнение ах 2 + b х + с = 0, где, а ≠ 0.
Умножая обе его части на, а, получаем уравнение
а 2 х 2 + а b х + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к
уравнению у 2 + by + ас = 0, равносильно данному.
Его корни у 1 и у 2 найдем с помощью теоремы Виета.
х 1 = у 1 /а и х 1 = у 2 /а.
При этом способе коэффициент, а умножается на
свободный член, как бы «перебрасывается» к нему,
поэтому его называют способом «переброски».
Этот способ применяют, когда можно легко найти
корни уравнения, используя теорему Виета и, что
самое важное, когда дискриминант есть точный
квадрат.
Свойства коэффициентов квадратного уравнения .
ах 2 + b х + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1, х 2 = с/а.
2)Если второй коэффициент b = 2 k – четное число, то формулу корней
можно записать в виде
0, два корня 2) D=0 , единственный корень 3) D 0, корней нет. " width="640"
Решение квадратных уравнений через дискриминант.
ах 2 + b х + с = 0, а ≠0
D=b 2 - 4 ac – дискриминант
1)D 0, два корня
2) D=0 , единственный корень
3) D 0, корней нет.
Пример:
,если
,если
,если
,если
Выделение полного квадрата двучлена
Пример:
Графическое решение квадратного уравнения.
х 2 + px + q = 0 , х 2 = - px - q .
Графики зависимости у = х 2 и у = - px - q .
График первой зависимости - парабола, проходящая через начало координат.
График второй зависимости – прямая.
Возможны следующие случаи:
- прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
- прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;
- прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
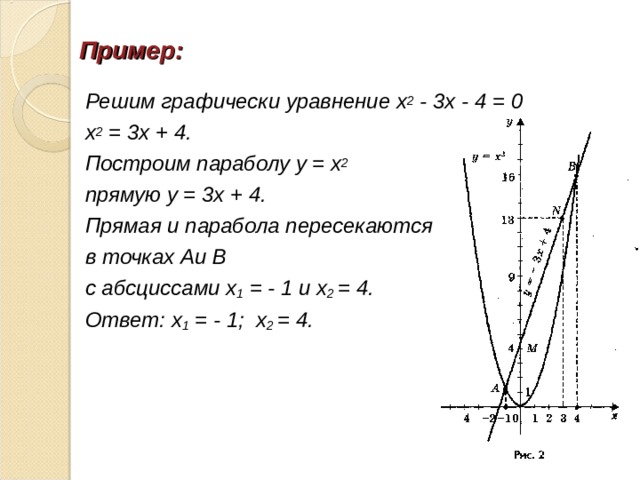
Пример:
Решим графически уравнение х 2 - 3х - 4 = 0
х 2 = 3х + 4.
Построим параболу у = х 2
прямую у = 3х + 4.
Прямая и парабола пересекаются
в точках Аи В
с абсциссами х 1 = - 1 и х 2 = 4.
Ответ: х 1 = - 1; х 2 = 4.
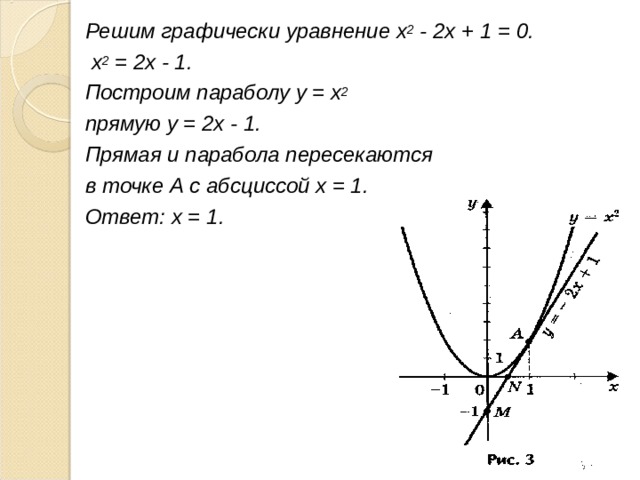
Решим графически уравнение х 2 - 2х + 1 = 0.
х 2 = 2х - 1.
Построим параболу у = х 2
прямую у = 2х - 1.
Прямая и парабола пересекаются
в точке А с абсциссой х = 1.
Ответ: х = 1.
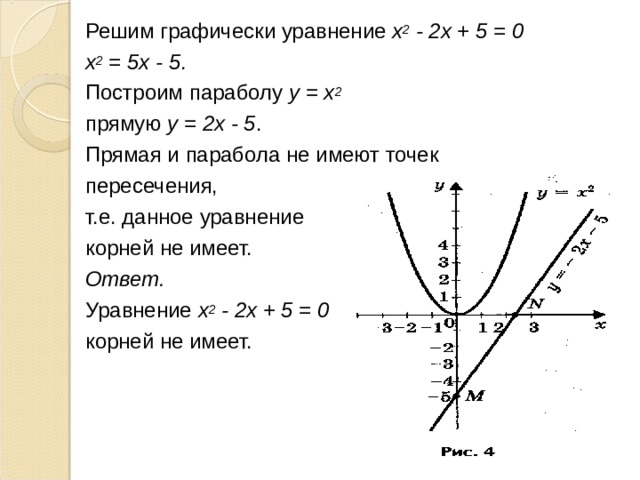
Решим графически уравнение х 2 - 2х + 5 = 0
х 2 = 5х - 5 .
Построим параболу у = х 2
прямую у = 2х - 5 .
Прямая и парабола не имеют точек
пересечения,
т.е. данное уравнение
корней не имеет.
Ответ.
Уравнение х 2 - 2х + 5 = 0
корней не имеет.
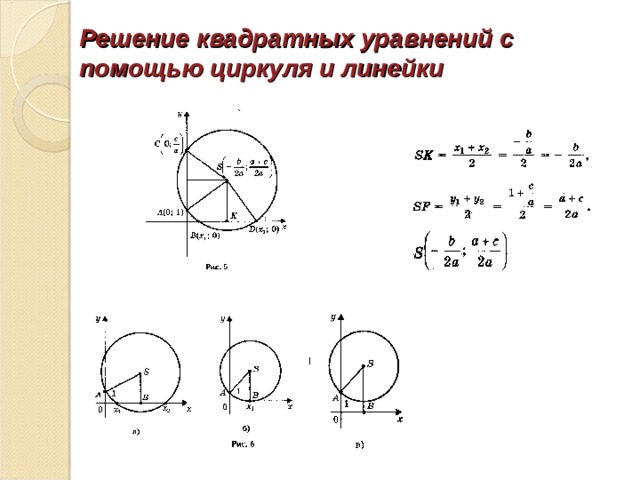
Решение квадратных уравнений с помощью циркуля и линейки
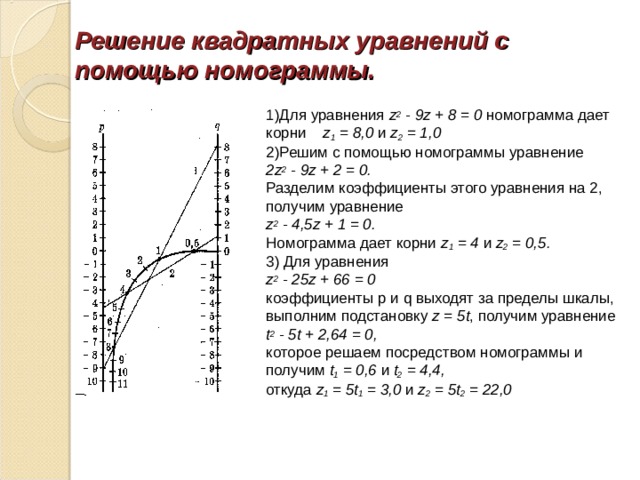
Решение квадратных уравнений с помощью номограммы.
1)Для уравнения z 2 - 9 z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0
2)Решим с помощью номограммы уравнение
2 z 2 - 9 z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z 2 - 4,5 z + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
3) Для уравнения
z 2 - 25 z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5 t , получим уравнение
t 2 - 5 t + 2,64 = 0,
которое решаем посредством номограммы и получим t 1 = 0,6 и t 2 = 4,4,
откуда z 1 = 5 t 1 = 3,0 и z 2 = 5 t 2 = 22,0
Геометрический способ решения квадратных уравнений
х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39»
Заключение:
Уравнения – язык алгебры, квадратные уравнения – это фундамент, на котором построено величественное здание алгебры. Изученные способы решения квадратных уравнений будут применяться и при дальнейшем изучении математики, при решении уравнений, сводящихся к решению квадратных. В ходе выполнения своей работы я считаю, что с поставленной целью и задачами я справилась, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.
Проанализировав все новые способы решения квадратных уравнений, я увидела, что нельзя однозначно сказать, какой именно метод наиболее удобен или совершенен. Все они хороши, но каждый в своем конкретном случае.
Я пришла к выводу, что все способы надо иметь в своем арсенале и применять их по мере необходимости с точки зрения рациональности решения .
Я составила буклет-памятку, в него вошли те способы решения квадратных уравнений, которые не изучаются в школе.
Нужно отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ОГЭ и ЕГЭ. Данные буклеты я раздам одноклассникам и ученикам других классов. Они могут воспользоваться собранными в буклет-памятку материалами для изучения и закрепления рациональных способов решения квадратных уравнений. В дальнейшем я планирую провести опрос, насколько интересна информация, предложенная в буклете, и используют ли они данные способы для решения квадратных уравнений, если да, то какой способ они считают наиболее простым и понятным
Литература:
1. Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. - М., Просвещение, 1981.
2. Брадис В.М. Четырехзначные математические таблицы для средней школы.Изд. 57-е. - М., Просвещение, 1990. С. 83.
3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. - М., высшая школа, 1969.
4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. - М., Просвещение, 1972.
5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. - М., Квант, № 4/72. С. 34.
6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. - 4-е, дополн. - М., Высшая школа, 1973.
7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. - М., Просвещение, 1970.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
