Конференция проектно-исследовательских работ учащихся
«Шаг в науку»
МАТЕМАТИКА
Удивительное о пропорциях
человеческого тела
Автор:
учащийся 9 класса
Хаманджи Никита
ВВЕДЕНИЕ
Эталонами красоты человеческого тела, образцами гармонического телосложения издавна считаются великие творения греческих скульпторов: Фидия, Поликтета, Мирона, Праксителя. Можно ли выразить красоту человека с помощью формул и уравнений? Математика дает утвердительный ответ. В создании своих творений греческие мастера использовали принцип золотой пропорции. Золотое сечение является мерилом гармонии в природе и в произведениях искусства на протяжении многих веков. Его изучением занимались люди античности и эпохи Возрождения. В ХIХ и ХХ веке интерес к золотому сечению возродился с новой силой.
Соответствуют ли современные люди тем идеальным пропорциям строения человеческого тела, которые дошли до нас с античных времен? На этот вопрос мы постараемся ответить в исследовательской работе «Золотое сечение в пропорциях тела человека».
Цель работы: изучение золотого сечения, как идеальной пропорции строения человеческого тела.
Задачи:
изучить литературу по теме исследовательской работы;
дать определение золотому сечению, познакомиться с его построением, применением и историей;
узнать математические закономерности в пропорциях тела человека;
научиться находить золотое сечение в пропорциях людей;
определить соответствие пропорций человеческого тела золотому сечению.
Гипотеза: пропорции каждого человеческого тела соответствуют золотому сечению.
Объект исследования: человек.
Предмет исследования: золотое сечение в пропорциях человеческого тела.
Методы исследования: измерение роста и частей тела человека, обработка полученных результатов математическими методами с помощью программы Microsoft Office Excel 2007, сравнительный анализ полученных измерений со значением золотого сечения.
Глава 1 Золотое сечение
Понятие золотого сечения
Пифагор показал, что отрезок единичной длины АВ (рисунок 1.1). можно разделить на две части так, что отношение большей части (АС=х) к меньшей (СВ=1-х) будет равняться отношению всего отрезка (АВ=1) к большей части(АС=х):
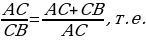
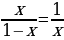

Рисунок 1.1 – Деление отрезка в крайнем и среднем отношении
По свойству пропорции .. х2=1-х,
х2+х-1=0. (1)
Положительным корнем этого уравнения является 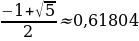 , так что отношения в приведенной пропорции равны:
, так что отношения в приведенной пропорции равны: 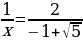 =
=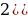 ≈1,61803 каждое.
≈1,61803 каждое.
Такое деление (точкой С) Пифагор называл золотым делением, или золотой пропорцией, Евклид – делением в крайнем и среднем отношении, а Леонардо да Винчи – общепринятым сейчас термином «золотое сечение».[7,с.18-19]
Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. [2,с.8]
Величину золотого сечения принято обозначать буквой Ф. Это сделано в честь Фидия- творца бессмертных скульптурных произведений. [1, с.141]
Ф=1,618033988749894. Это значение золотого сечения с 15 знаками после запятой. Более точное значение Ф можно увидеть в Приложении А.
Так как решение уравнения (1) является отношением между длинами частей отрезка, оно не зависит от длины самого отрезка. Другими словами, значение золотого сечения не зависит от первоначальной длины. [4, с.24,25]
Глава 2 Идеальные пропорции человеческого тела
Уже тысячелетия пытаются люди найти математические закономерности в пропорциях тела человека, прежде всего человека хорошо сложенного, гармоничного.
Древние греки, считавшие золотое сечение проявлением гармонии в природе, создавали статуи людей с соблюдением правила золотого сечения. В XIX веке профессор Цейзинг подтвердил это, измерив сохранившиеся до наших дней древнегреческие статуи. Цейзинг даже выделил части тела человека, которые, по его мнению, наиболее точно соответствуют золотому сечению. Если разделить тело человека согласно правилу золотого сечения, то линия пройдет в области пупка. Длина плеча относится к общей длине руки также согласно золотому сечению. Соотношение частей лица, длины фаланг пальцев руки и многие другие части тела подпадают под правило золотого сечения (рисунок 2.1). [3, с.24,25]
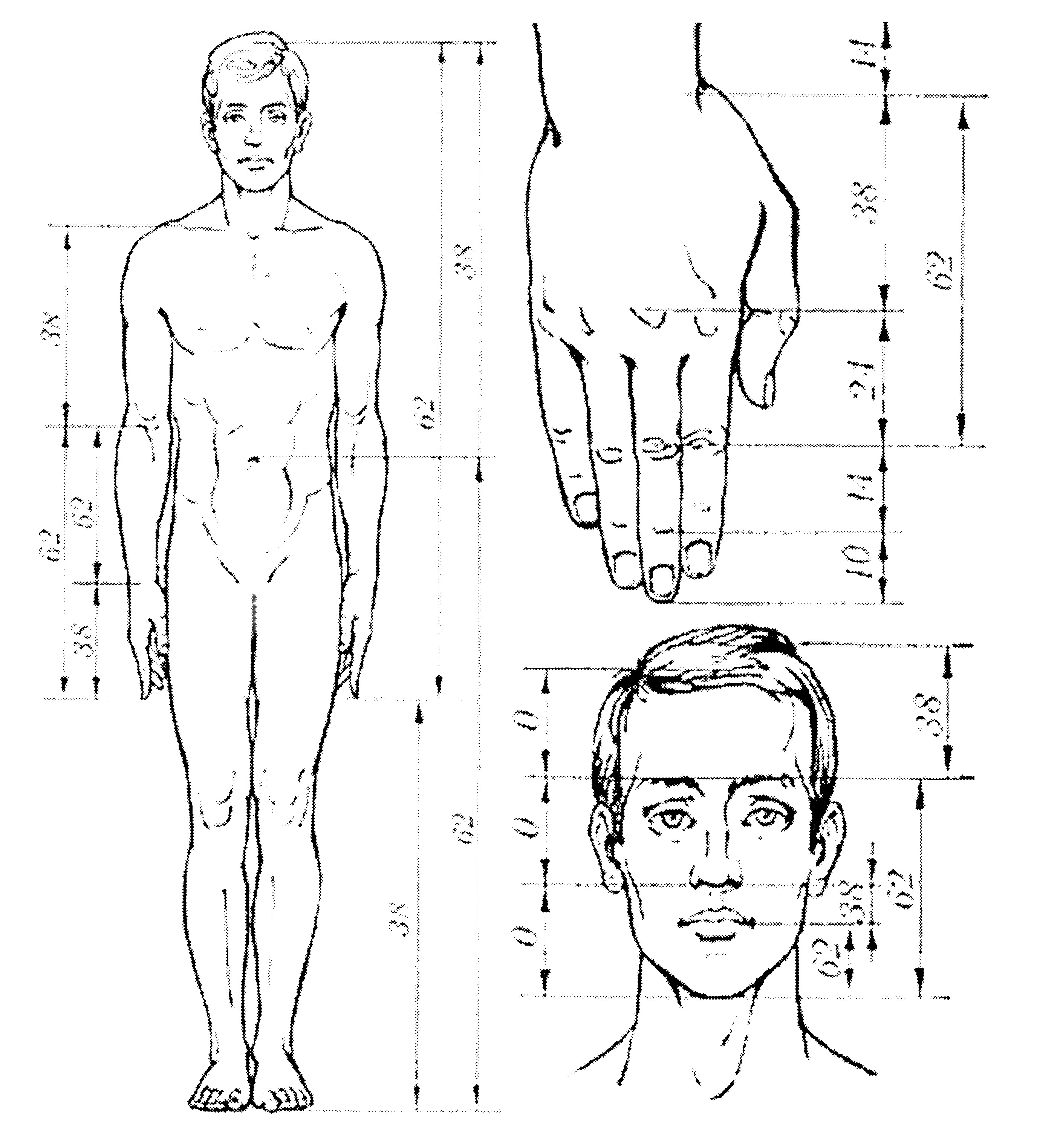
Рисунок 2.1 – Золотое сечение в строении тела человека
Золотая пропорция занимает ведущее место в художественных канонах Леонардо да Винчи и Дюрера. В соответствии с этими канонами золотая пропорция отвечает делению тела на две неравные части линией талии.
Высота лица (до корней волос) относится к вертикальному расстоянию между дугами бровей и нижней частью подбородка, как расстояние между нижней частью носа и нижней частью подбородка относится к расстоянию между углами губ и нижней частью подбородка, это отношение равно золотой пропорции.
Пальцы человека состоят из трех фаланг: основных, средних и ногтевых. Длина основных фаланг всех пальцев, кроме большого, равна сумме длин двух остальных фаланг, а длины всех фаланг каждого пальца соотносятся друг к другу по правилу золотой пропорции. [1, с.144,145]
Леонардо применил научные знания о пропорциях человеческого тела к теориям Пачоли и Витрувия о красоте. На рисунке Леонардо «Витрувианский человек» мужская фигура, вписанная в круг и квадрат (рисунок 2.2).
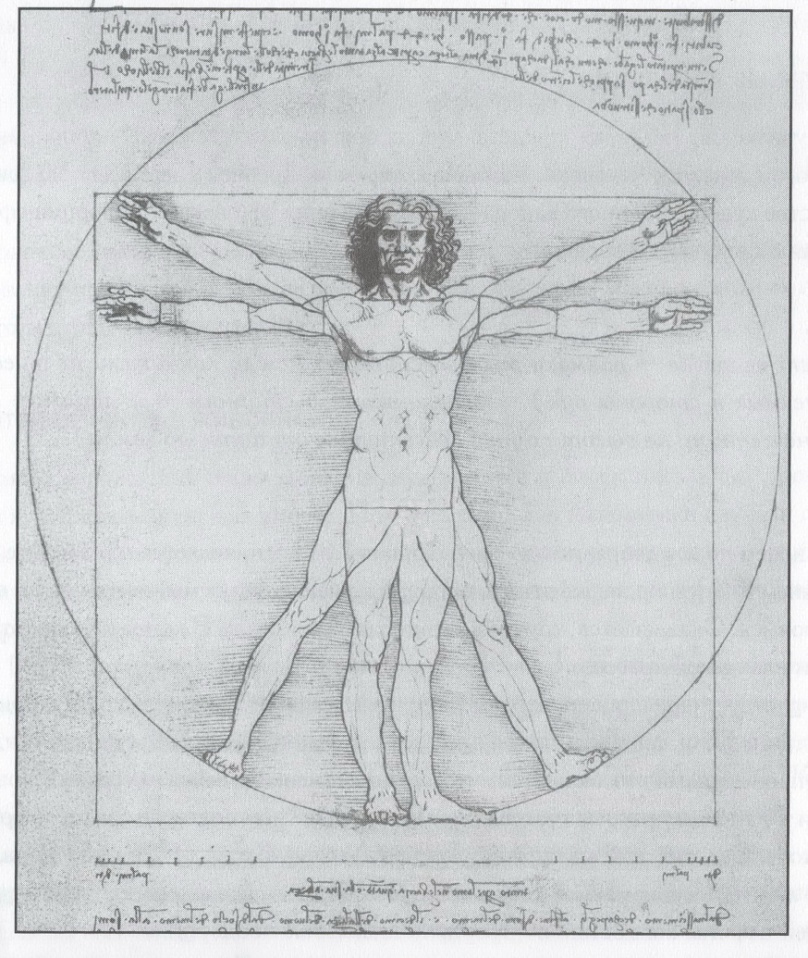
Рисунок 2.2 – «Витрувианский человек» Леонардо да Винчи
Квадрат и круг имеют разные центры. Гениталии человека являются центром квадрата, а пупок – центром круга. Идеальные пропорции человеческого тела на таком изображении соответствуют отношению между стороной квадрата и радиусом круга: золотому сечению. [4,с.100,101]
«Витрувианский человек» представляет собой приблизительные пропорции тела обычного взрослого человека, которые со времен Древней Греции использовались в качестве художественного канона для изображения человека. Пропорции сформулированы следующим образом:
Рост человека = размаху рук (расстоянию между кончиками пальцев разведенных в стороны рук) = 8 ладоням= 6 ступням= 8 лицам = 1,618 умноженному на высоту пупка (расстояние от пупка до земли).[4,с.102]
Одним из высших достижений классического греческого искусства может служить статуя «Дорифор» («Копьеносец»), изваянная Поликтетом (рисунок 2.3).
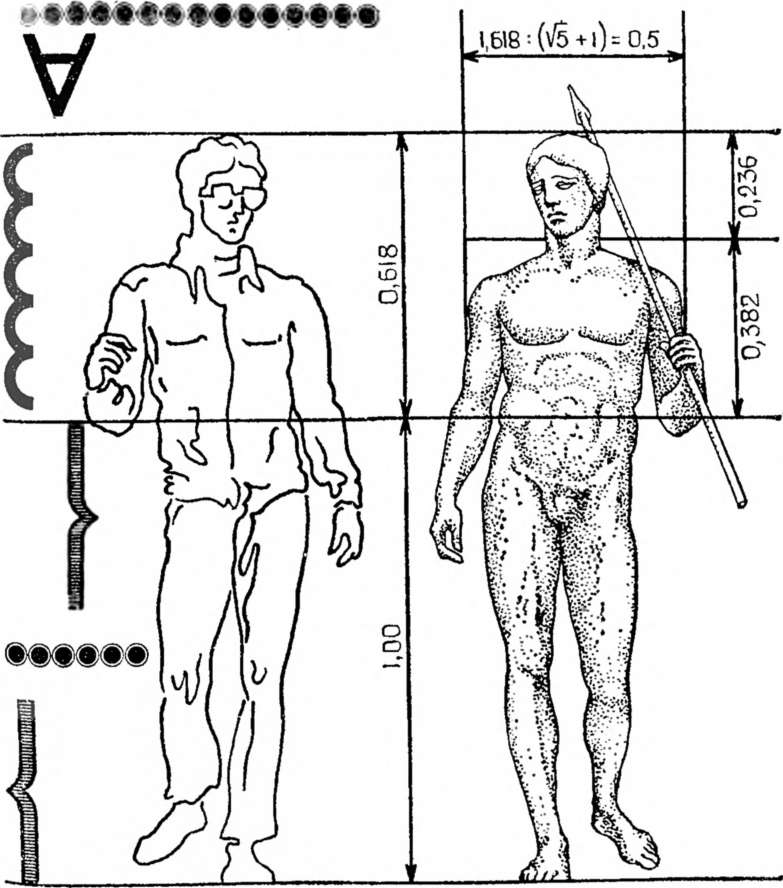
Рисунок 2.3 – Статуя «Дорифор» греческого скульптора Поликтета
Фигура юноши выражает единство прекрасного и доблестного, лежащих в основе греческих принципов искусства. Широкие плечи почти равны высоте туловища, половина высоты тела приходится на лонное сращение, высота головы восемь раз укладывается в высоте тела, а золотой пропорции отвечает положение пупка на теле атлета.[1,c.141,142]
В середине XIX века немецкий ученый Цейзинг находил, что все тело человека в целом и каждый отдельный его член связаны математически строгой системой пропорциональных отношений, среди которых золотое сечение занимает важнейшее место. Измерив тысячи человеческих тел, он установил, что золотая пропорция есть среднестатистическая величина, характерная для всех хорошо развитых тел. Средняя пропорция мужского тела близка к 13/8= 1,625, а женского — к 8/5=1,60, у новорожденного пропорция равна 2, к 13 годам она равна 1,6, а к 21 году равняется мужской (рисунок 2.4). [3, с.20]
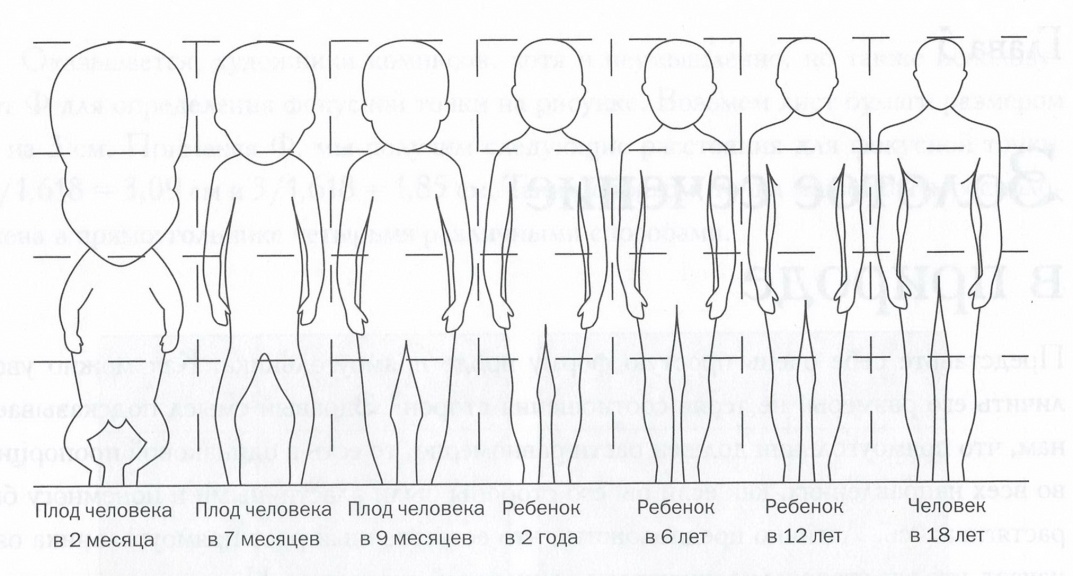
Рисунок 2.4 – Сравнение пропорций головы и тела человека на различных этапах развития [4,c.126]
Бельгийский математик Л.Кетле в XIX веке установил, что человек идеален только при подсчете среднего арифметического. В 1871г. его исследования пропорций тел жителей Европы полностью подтвердили идеальные пропорции.[4,с.102]
Золотую пропорцию можно считать некоторой «константой гармонии», идеальным пределом, к которому стремится тело человека в своем развитии.
Глава 3 Золотое сечение в пропорциях тела человека. Исследование
Мы проверяли гипотезу о том, что пропорции каждого человеческого тела соответствуют золотому сечению.
Для исследования были привлечены учащиеся 1-х, 5-х, 9-х и 11-х классов и учителя разного возраста (от 25 до 53 лет).
В теле человека пуп является точкой деления высоты тела в золотом сечении. Поэтому мы измеряли рост людей (a), высоту пупка (b) и расстояние от головы до пупка (c). Затем в программе Microsoft Office Excel 2007 находили отношения этих величин (a/b, b/c) для каждого человека в отдельности, cреднее значение для группы людей одного возраста (a/b), сравнивали отношения с величиной золотого сечения (1,618) и выбирали людей с золотой пропорцией (приложение Б).
Результаты исследования мы представили в виде таблицы (таблица 3.1).
Таблица 3.1 – Соответствие пропорций человеческого тела золотому сечению у людей разного возраста.
| Класс | Количество человек | Полученное среднеарифметическое отношение | Количество людей с золотой пропорцией |
| 1 | 11 | 1,701 | 0 |
| 5 | 14 | 1,652 | 0 |
| 9 | 19 | 1,640 | 2 |
| 11 | 8 | 1,622 | 1 |
| Учителя | 10 | 1,630 | 2 |
| 11 класс и учителя | 62 | 1,626 | 3 |
Наглядно эти данные можно представить в виде диаграмм (приложения В и Г).
По результатам проведенного исследования можно сделать следующие выводы:
с возрастом у человека пропорции тела изменяются;
пропорции тела человека отличаются даже у людей одного возраста;
у взрослых людей пропорции тела приближаются к величине золотого сечения, но редко соответствует ему;
идеальные пропорции золотого сечения не применимы ко всем людям.
Следовательно, золотое сечение в пропорциях тела человека - это среднестатистическая величина, к которой приближаются пропорции тела взрослого человека. Только у некоторых людей пропорции тела соответствуют золотому сечению.
ЗАКЛЮЧЕНИЕ
Золотое сечение является мерилом гармонии в природе и в произведениях искусства на протяжении многих веков. Учение о золотом сечении получило широкое применение в математике, физике, химии, живописи, эстетике, биологии, музыке, технике.
Целью исследовательской работы было изучение золотого сечения, как идеальной пропорции строения человеческого тела.
Для достижения цели мы изучили литературу по теме исследовательской работы, познакомились с золотым сечением, с его построением, применением и историей; узнали математические закономерности в пропорциях тела человека; научились находить золотое сечение в пропорциях людей (приложение Д).
В практической части мы определяли соответствие пропорций человеческого тела золотому сечению, проверяли следующую гипотезу: пропорции каждого человеческого тела соответствуют золотому сечению.
Для проверки гипотезы мы измеряли рост людей и некоторые части тела у учащихся 1, 5, 9, 11 классов и учителей разного возраста.. Затем в программе Microsoft Office Excel 2007 находили отношения величин для каждого человека в отдельности, cреднее значение для группы людей одного возраста, сравнивали полученные отношения со значением золотого сечения и выбирали людей с золотой пропорцией.
На основании результатов проведенного исследования можно сделать следующие выводы:
с возрастом у человека пропорции тела изменяются;
пропорции тела человека отличаются даже у людей одного возраста;
у взрослых людей пропорции тела приближаются к величине золотого сечения, но редко соответствует ему;
идеальные пропорции золотого сечения не применимы ко всем людям.
Следовательно, золотое сечение в пропорциях тела человека - это среднестатистическая величина, к которой приближаются пропорции тела взрослого человека. Только у некоторых людей пропорции тела соответствуют золотому сечению. Наша гипотеза подтвердилась частично.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Васютинский, Н.А. Золотая пропорция / Н.А.Васютинский – М.: Мол. гвардия, 1990. – 238 с.
Ковалев, Ф.В.Золотое сечение в живописи: учеб. пособие/ Ф.В. Ковалев. - К.:Выща школа. Головное изд-во, 1989.—143 с.
Лукашевич, И.Г. Математика в природе /И.Г. Лукашевич. -Минск: Белорус. ассоц. «Конкурс», 2013. - 48с.
Мир математики: в 40т. Т.1: ФернандоКорбалан. Золотое сечение. Математический язык красоты /Пер.с англ. - М.:Де Агостини, 2014. - 160с.
Стахов, А.П. Коды золотой пропорции/А.П. Стахов. - М.: «Радио и связь»,1984. – 152с.
Тимердинг, Г.Е. Золотое сечение /Г.Е.Тимердинг; под ред. Г.М.Фихтенгольца; пер. с нем.- Петроград: Научное книгоизд-во, 1924. – 86с.
Урманцев, Ю.А. Симметрия природы и природа симметрии /Ю.А.Урманцев. - М.,Мысль,1974. - 229с.
Я познаю мир: Дет.энцикл: Математика /Авт.-сост. А.П.Савин и др.; худож.А.В.Кардашук и др. - М.: АСТ: Астрель, 2002. - 475с.
ПРИЛОЖЕНИЕ А
ЗНАЧЕНИЕ ЗОЛОТОГО СЕЧЕНИЯ

Рисунок А.1 – Более точное значение Ф
ПРИЛОЖЕНИЕ Б
СООТВЕТСТВИЕ ПРОПОРЦИЙ ЧЕЛОВЕЧЕСКОГО ТЕЛА ЗОЛОТОМУ СЕЧЕНИЮ
Таблица Б.1-Результаты измерения людей и вычисление среднеарифметических значений пропорций тела для учащихся 1, 5, 9, 11 классов и учителей
|
| Фамилия Имя | Класс
| Рост (а) | Высота линии пупка (b) | Рассто-яние от пупка до головы (с) | а/b | b/c | Среднее арифме- тическое значение (a/b) |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|
| Золотое сечение |
|
|
|
| 1,618 | 1,618 |
|
| 1 | Андреев Владислав | 1а | 130 | 77 | 53 | 1,688 | 1,453 |
|
| 2 | Грабцевич Дарья | 1а | 125 | 71 | 54 | 1,760 | 1,315 |
|
| 3 | Ваванова Дарья | 1а | 127 | 74 | 53 | 1,716 | 1,396 |
|
| 4 | Захаренко Родион | 1а | 124 | 74 | 50 | 1,676 | 1,480 | 1класс |
| 5 | Капориков Даниил | 1а | 133 | 79 | 54 | 1,684 | 1,463 | 1,701 |
| 6 | Карсаков Захар | 1а | 120 | 71 | 49 | 1,690 | 1,449 |
|
| 7 | Лазовый Максим | 1а | 128 | 75 | 53 | 1,707 | 1,415 |
|
| 8 | Ласоцкая Анна | 1а | 125 | 76 | 49 | 1,645 | 1,551 |
|
| 9 | Моргунова Мария | 1а | 116 | 66 | 50 | 1,758 | 1,320 |
|
| 10 | Павлющенко Егор | 1а | 129 | 77 | 52 | 1,675 | 1,481 |
|
| 11 | Раковский Александр | 1а | 128 | 75 | 53 | 1,707 | 1,415 |
|
| 12 | Бахарева Ксения | 5а | 146 | 87 | 59 | 1,678 | 1,475 |
|
| 13 | Бытковский Максим | 5а | 145 | 85 | 60 | 1,706 | 1,417 |
|
| 14 | Жданович Виктория | 5а | 146 | 86 | 60 | 1,698 | 1,433 | 5класс |
| 15 | Климова Ксения | 5а | 155 | 95 | 60 | 1,632 | 1,583 | 1,652 |
| 16 | Ларченко Евгения | 5а | 158 | 94 | 64 | 1,681 | 1,469 |
|
| 17 | Листвягов Сергей | 5а | 143 | 87 | 56 | 1,644 | 1,554 |
|
| 18 | Мухина Анастасия | 5а | 144 | 88 | 56 | 1,636 | 1,571 |
|
| 19 | Падерина Анастасия | 5а | 151 | 91 | 60 | 1,659 | 1,517 |
|
| 20 | Прочуханов Денис | 5а | 151 | 92 | 59 | 1,641 | 1,559 |
|
| 21 | Савкина Анастасия | 5а | 140 | 87 | 53 | 1,609 | 1,642 |
|
| 22 | Симакович Алевтина | 5а | 137 | 84 | 53 | 1,631 | 1,585 |
|
| 23 | Сурганова Дарья | 5а | 150 | 92 | 58 | 1,630 | 1,586 |
|
| 24 | Смоляров Владислав | 5а | 142 | 86 | 56 | 1,651 | 1,536 |
|
| 25 | Тихинский Александр | 5а | 144 | 88 | 56 | 1,636 | 1,571 |
|
| 26 | Аверков Алексей | 9а | 171 | 104 | 67 | 1,644 | 1,552 |
|
Продолжение таблицы Б.1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 27 | Власенко Анастасия | 9а | 162 | 99 | 63 | 1,636 | 1,571 |
|
| 28 | Гелясов Евгений | 9а | 194 | 115 | 79 | 1,687 | 1,456 |
|
| 29 | Герасимов Евгений | 9а | 177 | 108 | 69 | 1,638 | 1,565 | 9класс |
| 30 | Дудкова Яна | 9а | 163 | 100 | 63 | 1,630 | 1,587 | 1,640 |
| 31 | Кондратенко Андрей | 9а | 167 | 102 | 65 | 1,637 | 1,569 |
|
| 32 | Лихачева Александра | 9а | 158 | 99 | 59 | 1,596 | 1,678 |
|
| 33 | Мелашунас Дарья | 9а | 165 | 102 | 63 | 1,618 | 1,619 |
|
| 34 | Романова Диана | 9а | 165 | 103 | 62 | 1,602 | 1,661 |
|
| 35 | Савкина Александра | 9а | 171 | 104 | 67 | 1,644 | 1,552 |
|
| 36 | Свищев Кирилл | 9а | 172 | 105 | 67 | 1,638 | 1,567 |
|
| 37 | Свищева Анастасия | 9а | 162 | 99 | 63 | 1,636 | 1,571 |
|
| 38 | Смирнова Татьяна | 9а | 160 | 98 | 62 | 1,633 | 1,581 |
|
| 39 | Шкель Роман | 9а | 172 | 106 | 66 | 1,623 | 1,606 |
|
| 40 | Алейников Егор | 9б | 184 | 110 | 74 | 1,673 | 1,486 |
|
| 41 | Гегелева Ксения | 9б | 164 | 99 | 65 | 1,657 | 1,523 |
|
| 42 | Димков Анатолий | 9б | 163 | 99 | 64 | 1,647 | 1,547 |
|
| 43 | Рябцева Евгения | 9б | 170 | 103 | 67 | 1,651 | 1,537 |
|
| 44 | Тарасенко Анатолий | 9б | 162 | 97 | 65 | 1,670 | 1,492 |
|
| 45 | Дудов Роман | 11а | 165 | 101 | 64 | 1,634 | 1,578 |
|
| 46 | Земцова Дарья | 11а | 161 | 101 | 60 | 1,594 | 1,683 | 11класс |
| 47 | Ивлев Никита | 11а | 176 | 109 | 67 | 1,615 | 1,627 | 1,622 |
| 48 | Розенберг Анастасия | 11а | 161 | 101 | 60 | 1,594 | 1,683 |
|
| 49 | Цедрик Анна | 11а | 158 | 96 | 62 | 1,646 | 1,548 |
|
| 50 | Шевченко Савелий | 11а | 182 | 111 | 71 | 1,640 | 1,563 |
|
| 51 | Шевчуковская Елена | 11а | 164 | 102 | 62 | 1,608 | 1,645 |
|
| 52 | Яковишин Никита | 11а | 179 | 109 | 70 | 1,642 | 1,557 |
|
| 53 | Белогривцев В.В. | учит. | 173 | 104 | 69 | 1,664 | 1,507 | Учителя |
| 54 | Булай Е.И. | учит. | 163 | 101 | 62 | 1,614 | 1,629 | 1,630 |
| 55 | Волкова О.В. | учит. | 164 | 100 | 64 | 1,64 | 1,563 |
|
| 56 | Гриневская Н.А. | учит. | 166 | 101 | 65 | 1,644 | 1,554 |
|
| 57 | Гринченко Е.Б. | учит. | 162 | 99 | 63 | 1,636 | 1,571 |
|
| 58 | Киреенко А.С. | учит. | 175 | 108 | 67 | 1,620 | 1,612 |
|
| 59 | Стукалов Д.М. | учит. | 165 | 101 | 64 | 1,634 | 1,578 | 11класс и учителя |
| 60 | Цедрик Н.Е. | учит. | 158 | 96 | 62 | 1,646 | 1,548 |
| 61 | Шкоркина Н.Н. | учит. | 165 | 103 | 62 | 1,602 | 1,661 | 1,626 |
| 62 | Яценко В.Н. | учит. | 162 | 101 | 61 | 1,604 | 1,656 |
|
ПРИЛОЖЕНИЕ В
РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЯ ПРОПОРЦИЙ ТЕЛА У ЛЮДЕЙ РАЗНОГО ВОЗРАСТА
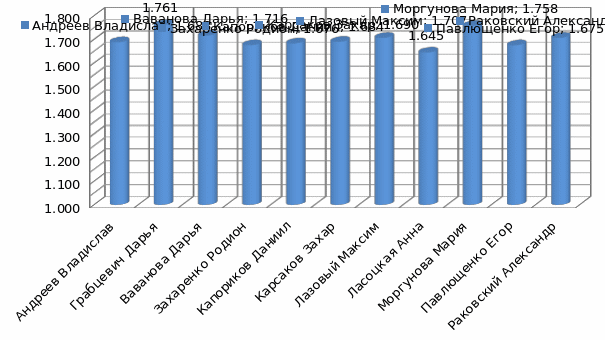
Рисунок В.1 – Результаты вычисления пропорций тела у учащихся 1 класса
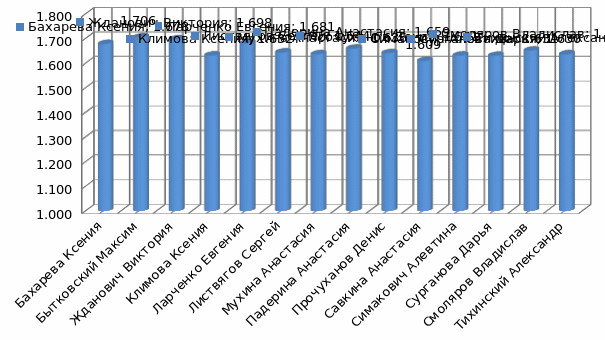
Рисунок В.2 – Результаты вычисления пропорций тела у учащихся 5 класса
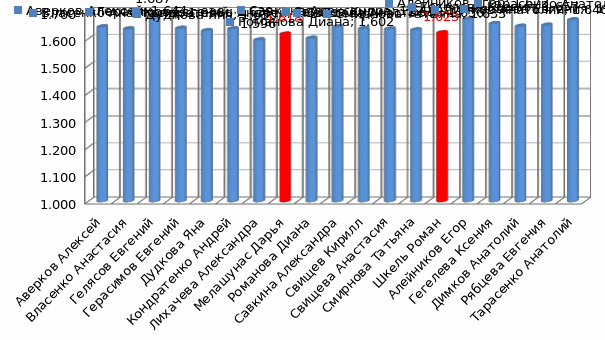
Рисунок В.3 – Результаты вычисления пропорций тела у учащихся 9 класса
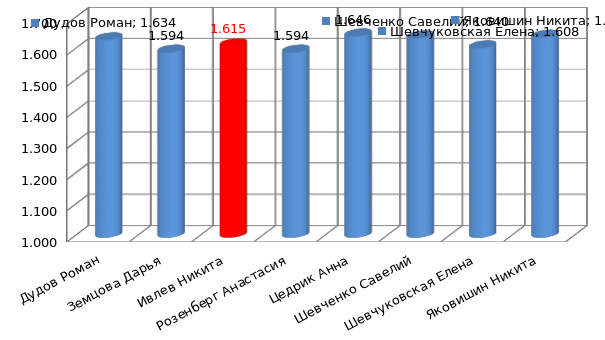
Рисунок В.4 – Результаты вычисления пропорций тела у учащихся 11 класса
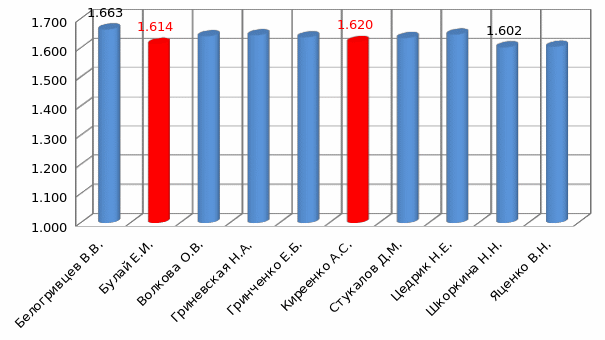
Рисунок В.5 – Результаты вычисления пропорций тела у учителей
ПРИЛОЖЕНИЕ Г
СРАВНЕНИЕ ПРОПОРЦИЙ ТЕЛА ЛЮДЕЙ РАЗНОГО ВОЗРАСТА
СО ЗНАЧЕНИЕМ ЗОЛОТОГО СЕЧЕНИЯ
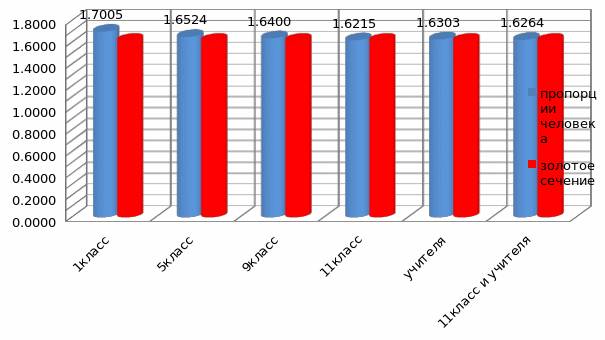
Рисунок Г.1 – Сравнение средних пропорций тела людей разного возраста со значением золотого сечения
ПРИЛОЖЕНИЕ Д
ЭТАПЫ РАБОТЫ НАД ИССЛЕДОВАНИЕМ



а) б) в)
Рисунок Д.1 - Изучение литературы



а) б) в)


г) д)
Рисунок Д.2 - Проведение измерений учащихся и учителей

Рисунок Д.3 – Ввод и обработка полученных данных
33






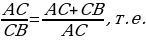
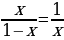

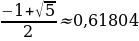 , так что отношения в приведенной пропорции равны:
, так что отношения в приведенной пропорции равны: 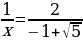 =
=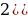 ≈1,61803 каждое.
≈1,61803 каждое. 





























