Муниципальное образовательное учреждение
«Средняя школа № 46»
Школьная научно-практическая конференция
Волшебные свойства клетчатой бумаги
Антипов Дмитрий,
ученик 6 «Б» класса
Бойцева Ирина Юрьевна,
учитель математики
Петрозаводск
2012
Оглавление
| Введение………………………………………………………………….… | 3
|
| Основная часть……………………………………………………………. | 4-10
|
| 1. Исторические факты | 4
|
| 2. Геометрия клетчатой бумаги | 5-6
|
| 3. Формула Пика | 7-8
|
| 4. Окружность без циркуля | 9 |
| 5. Клетка для развития детей. | 10 |
| 6. Координатная плоскость | 11 |
| Заключение | 12
|
| Использованная литература | 13 |
Введение.
Тема нашего исследования – «Волшебные свойства клетчатой бумаги». Почему тетрадь по математике в клеточку? Почему именно клетчатая поверхность листа стала настоящей помощницей математики? Что позволяют делать клетки обычной тетради? Каким образом они позволяют совершать ей необыкновенные чудеса?
Объект исследования: Свойства клетчатой бумаги
Предмет исследования: Тетрадь по математике.
Цель: Узнать, почему тетрадь по математике в клетку
Задачи:
проанализировать информационные ресурсы по указанной теме;
изучить и обобщить некоторые интересные свойства клетки;
создать презентацию по теме исследования.
Гипотеза: Клетчатая бумага помогает тетради по математике делать чудеса
Методы исследования, использованные в работе:
1. Опрос по теме исследования
2. Анализ литературы по теме.
3. Обобщение материала.
1.Исторические факты
Пожалуй, именно бумага явилась главным материалом, из которого построен современный мир. Сказки и романы, азбука и учебники, тетради и дневники, газеты и журналы, блокноты и ежедневники, листовки и плакаты. Список бумажных слагаемых нашей жизни можно продолжать и продолжать.
Философы древности вывели великую формулу совершенства – чистый лист! И по сей день, эта формула будоражит умы взрослых и детей, потому что чистый лист бумаги предлагает, просит, требует заполнения.
Предметом нашего исследования стала обычная тетрадь по математике. Почему именно клетчатая поверхность заполнила её листы? Математика – удивительная наука! И мы рискнули предположить, что клетчатая бумага, обладая волшебными свойствами, помогает ей делать настоящие чудеса.
«На Руси писали на коре деревьев и на вощёных табличках с помощью палочек, сделанных из веток. И только в XIV веке появилась бумага из хлопка и льна. Однако тетради из такой тряпичной бумаги были очень дорогим удовольствием. Они были только у детей состоятельных людей.
Такая бумага, какой мы её знаем сегодня появилась в России только в середине XVI века, но расцвет бумажного производства наступил при Петре Первом. По его указу были построены первые предприятия по производству бумаги под Москвой и Санкт-Петербургом.
Тетради отечественного производства появились в России только в начале XVIII века. Они были настоящими произведениями искусства – с расписной обложкой и водяными знаками на каждой странице. Но тогда тетрадей в клетку не было – только в линейку.
В Советском Союзе у всех школьников были одинаковые тетради – со стандартной неяркой обложкой и текстом гимна с обратной стороны. Сегодня же в магазинах – огромный выбор тетрадей». [1]

2. Геометрия клетчатой бумаги
Так почему же тетрадь по математике в клеточку?
Не все люди, которым мы задавали этот вопрос, сразу же могли дать нам вразумительный ответ. Но ответ одного первоклассника всё-таки поразил нас и стал главным толчком нашего дальнейшего исследования. Тот самый ученик 1 класса нашей школы мгновенно произнёс: «Клетка – помощница старшеклассников, потому что две клетки это 1 см».
Наверное, она нужна и для того, чтобы удобно было записывать примеры в столбик, и чтобы легче было чертить. «Клеточки на бумаге позволяют многие построения проводить только с помощью одной линейки, на которой может даже не быть делений. Нужно только помнить свойства геометрических фигур, ведь именно они позволяют использовать клеточки в полной мере». [2] И вот, что мы нашли!
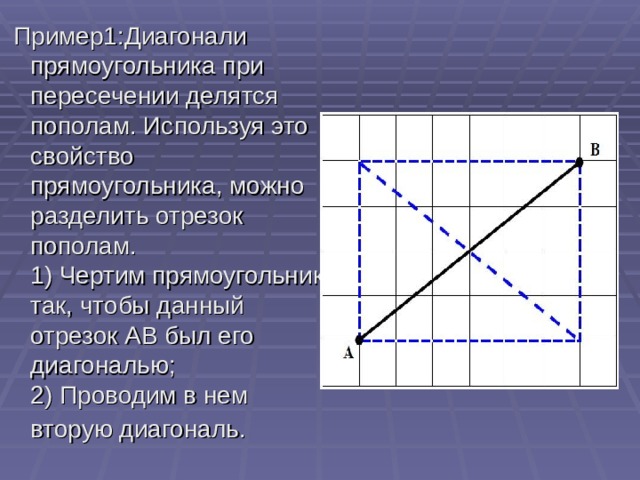
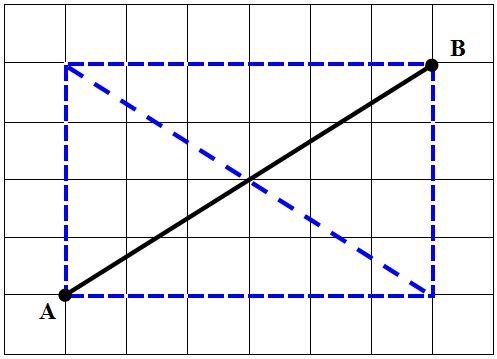
Пример 1. Диагональ прямоугольника – это отрезок, соединяющий противоположные вершины. Диагонали прямоугольника при пересечении делятся пополам. Используя это свойство прямоугольника, можно разделить отрезок пополам.
1) Чертим прямоугольник так, чтобы данный отрезок АВ был его диагональю;
2) Проводим в нем вторую диагональ. Она разделит наш отрезок АВ пополам.
Смотри рисунок.
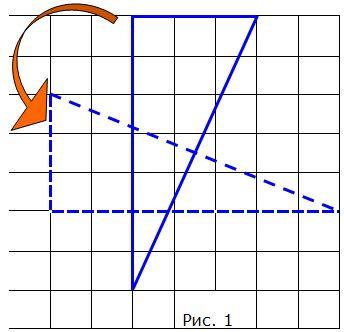
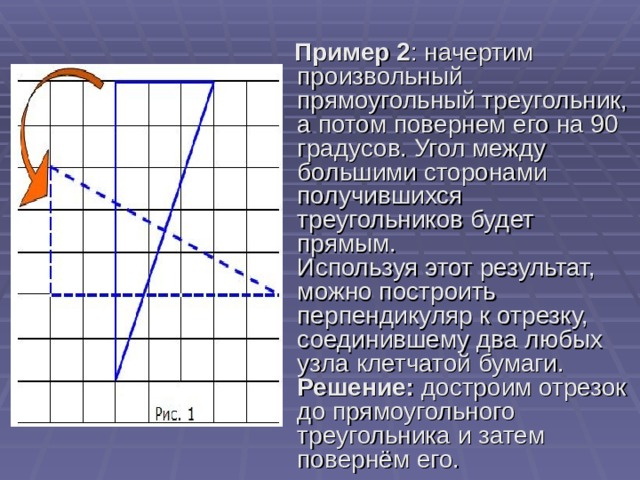
Пример 2: начертим произвольный прямоугольный треугольник (рис. 1), а потом поверните его на 900. Угол между большими сторонами получившихся треугольников равен 900.
Используя этот результат, можно построить перпендикуляр к отрезку, соединившему два любых узла клетчатой бумаги.
Решение: достроим отрезок до прямоугольного треугольника и затем повернём его, как в рассмотренном примере 2.
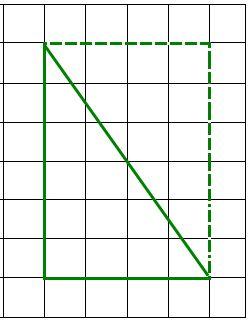
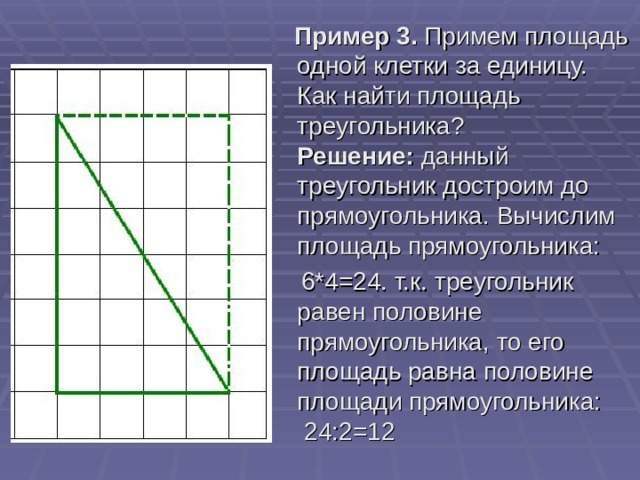
Пример 3. Примем площадь одной клетки за единицу. Как найти площадь треугольника?
Решение: данный треугольник достроим до прямоугольника. Вычислим площадь прямоугольника:
6*4=24. т.к. треугольник равен половине прямоугольника, то его площадь равна половине площади прямоугольника: 24:2=12
Значит и правда клетка помогает! И строить! И измерять! Ведь клетка это квадрат. Его сторонами можно измерять длины отрезков, а самими квадратами можно измерять площадь. Но главное волшебство клетки мы открыли в её узлах - точках, являющихся вершинами квадратов-клеток. Об этом нашем открытии пойдёт речь в следующей главе.
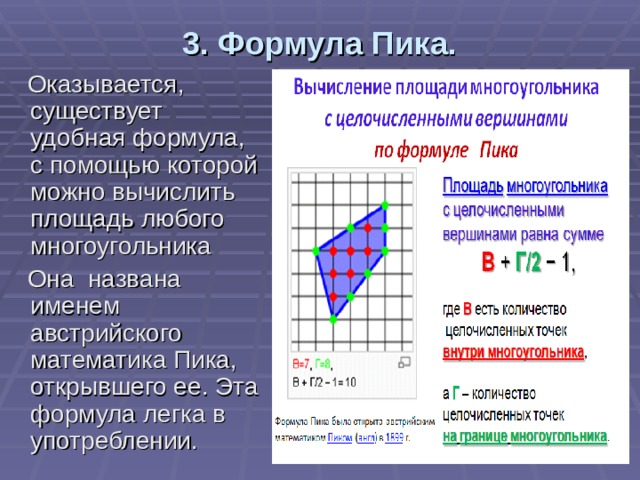
3. Формула Пика.
Оказывается, существует удобная формула, с помощью которой можно вычислить площадь любого многоугольника. Эта формула называется формулой Пика. И здесь снова не обойтись без клетки.
Формула Пика была открыта немецким математиком Пиком в 1899 г.
Теорема Пика. Пусть В — число целочисленных точек внутри многоугольника, Г— количество целочисленных точек на его границе, 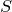 — его площадь. Тогда справедлива формула Пика:
— его площадь. Тогда справедлива формула Пика:
S = В + 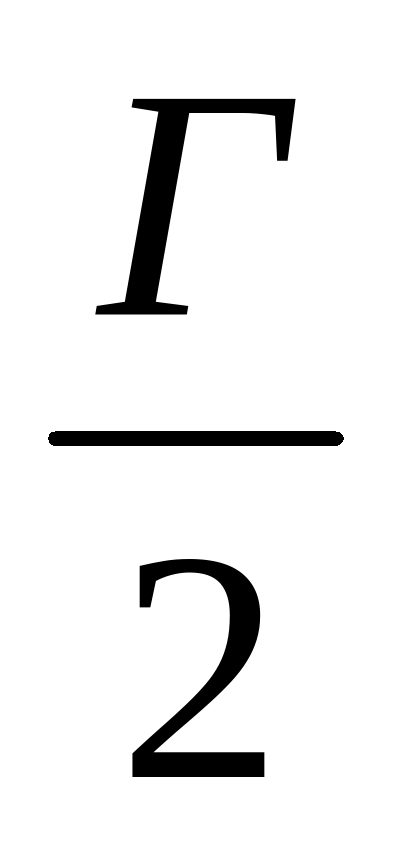 - 1 .
- 1 .
Задачи на применение формулы Пика.
Задача 1. Найдите площадь прямоугольника АВСD (рис.4).
Р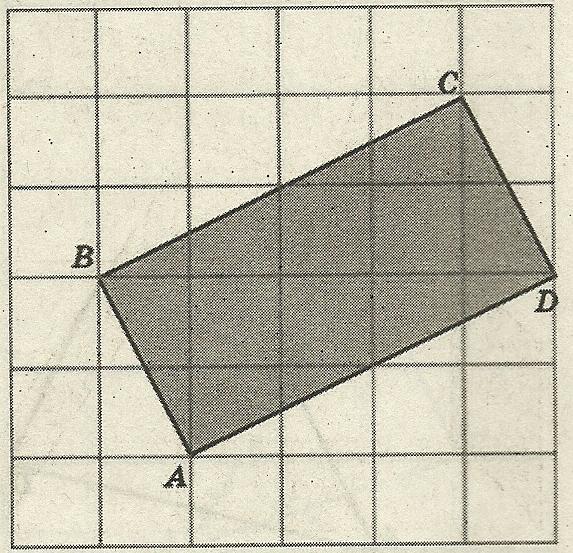 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 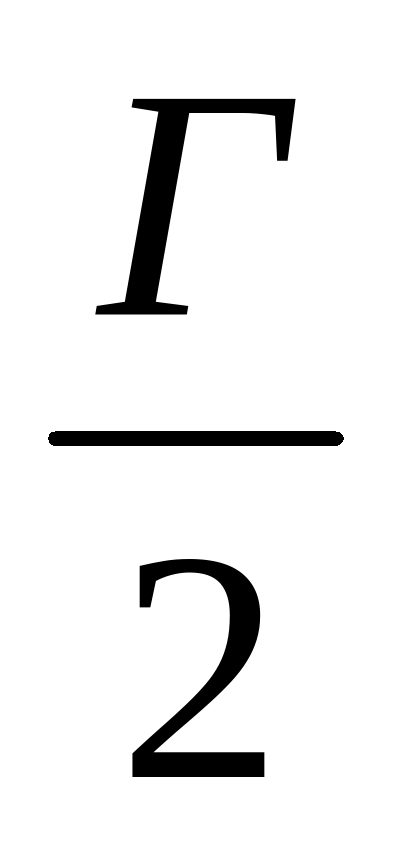 - 1 .
- 1 .
В = 8, Г = 6
Рис. 4 S = 8 + 6/2 – 1 = 10 (см²)
Ответ: 10 см².
Задача 2. Найдите площадь параллелограмма АВСD (рис.5)
Р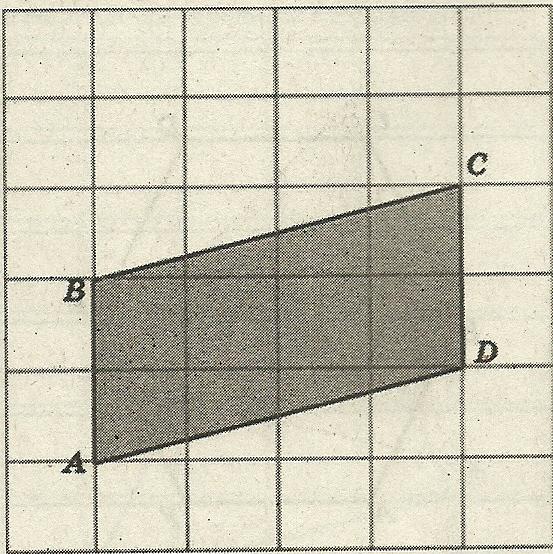 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 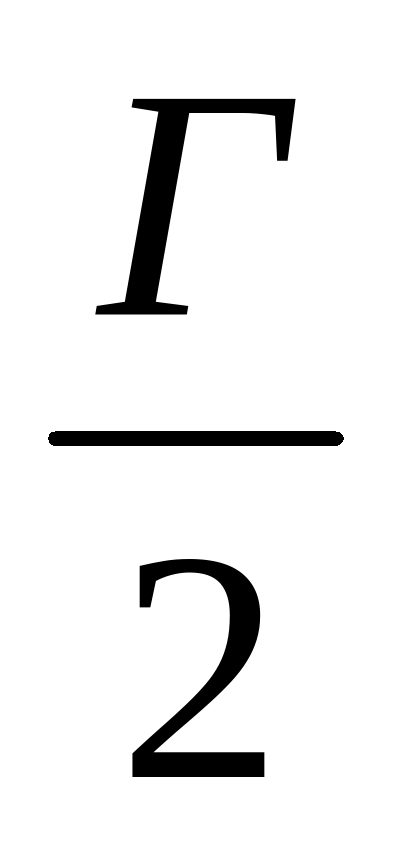 - 1 .
- 1 .
В = 6, Г = 6
S = 6 + 6/2 – 1 = 8 (см²)
Рис. 5 Ответ: 8 см².
Задача 3. Найдите площадь треугольника АВС (рис.6)
Р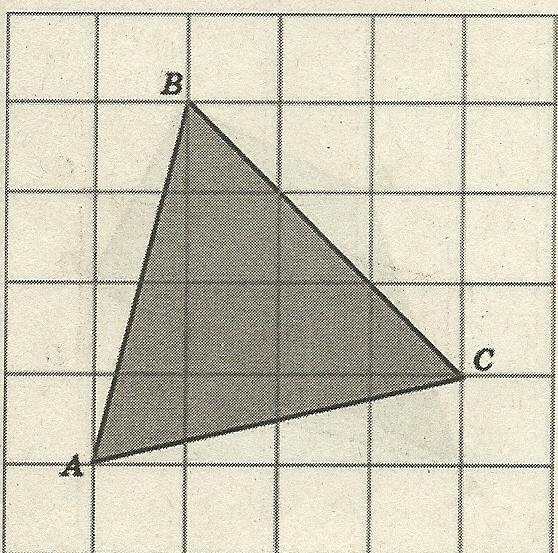 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 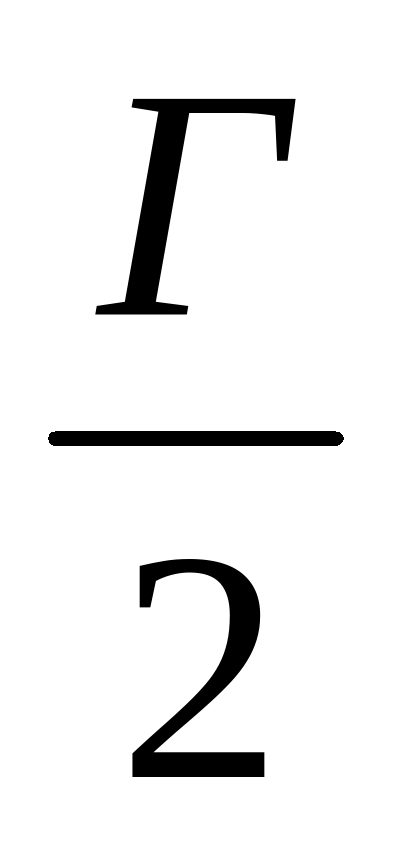 - 1 .
- 1 .
В = 6, Г = 5
S = 6 + 5/2 – 1 = 7,5 (см²)
Рис. 6 Ответ: 7,5 см².
Задача 4. Найдите площадь четырёхугольника АВСD (рис. 7)
Р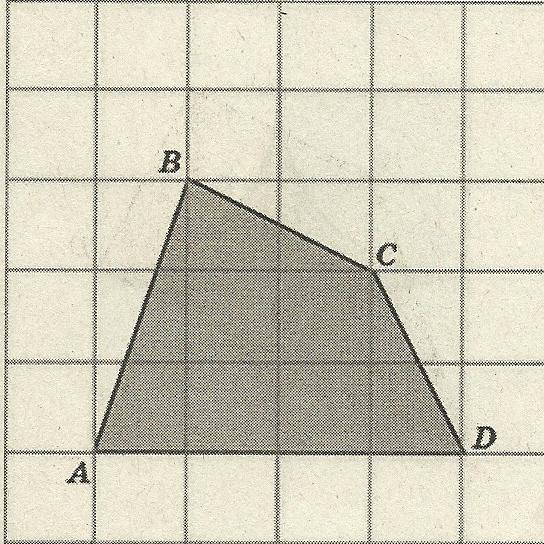 ешение. По формуле Пика: S = В +
ешение. По формуле Пика: S = В + 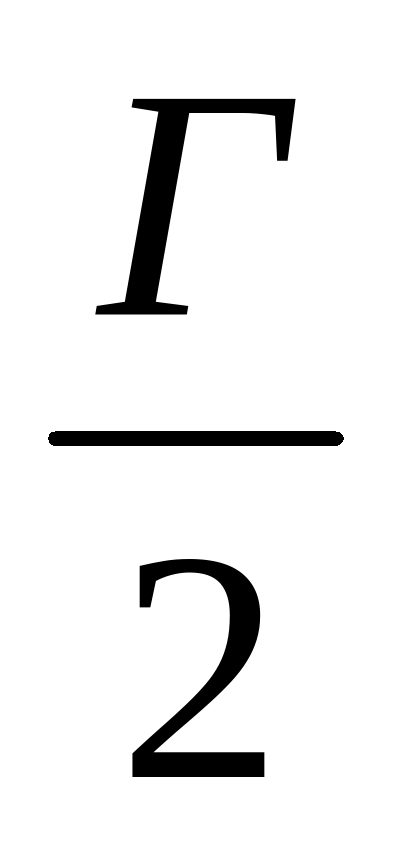 - 1 .
- 1 .
В = 5, Г = 7
S = 5 + 7/2 – 1 = 7,5 (см²)
Рис. 7 Ответ: 7,5 см².
С этим нашим открытием мы уже поделились с учителем математики 11 классов нашей школы. Ведь при решении одного из заданий ЕГЭ, в котором нужно найти площадь многоугольника, можно использовать Формулу Пика, которая даёт для многих задач простое и быстрое решение!
Разве это не волшебство?
Но узлы клеток приходят на помощь не только здесь.
4.Окружность без циркуля.
Известно, что для изображения окружности служит циркуль. Гораздо труднее нарисовать окружность без него. Для этого нужен опыт. Однако клетчатая бумага и здесь приходит на помощь.
«При изображении окружности на клетчатой бумаге стоит запомнить одно правило, позволяющее сделать нужное изобретение от руки. Правда речь идёт об изображении окружности определённого размера. Правило это записывается в виде трёх пар чисел: 3-1, 1-1, 1-3. Это как волшебные слова «крибли-крабли-бумс»…
Действовать по этому правилу нужно так. Возьмём пересечение линий (узел) клеток клетчатой бумаги (см. рис.). Отступив на три клетки вправо и одну вниз, поставим вторую точку. Отступая от второй точки по одной клетке вправо и вниз, находим третью точку. Четвёртая точка находится в одной клетке вправо и трёх вниз от третьей точки. Соединив плавной линией полученные точки, мы получим четверть окружности». Далее, продолжив аналогичные построения, получим окружность. [3]
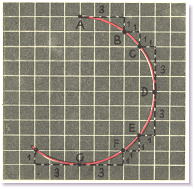
Радиус такой окружности равен 2,5 см.или 5 клеток.
5. Клетка для развития детей.
Клетка помогает нам с детства. Стоит произнести в определённом порядке волшебные слова: «влево – вправо – вниз – вверх», как тут же появится изображение чего-либо.
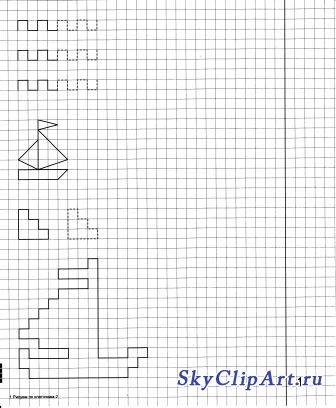
Попробуйте и вы вернуться в детство.
Отступите 3 клетки слева, 10 клеток сверху, поставьте точку и начинайте рисовать:
1клетка - вправо, 7 клеток – вверх, 4 клетки – вправо, 1 клетка – вниз,
5 клеток – вправо, 8 клеток - вниз, 3 клетки – влево, 3 клетки – вверх,
1 клетка – влево, 3 клетки – вниз, 3 клетки – влево, 4 клетки – вверх,
1 клетка – влево, 3 клетки – вниз, 2 клетки – влево, 1 клетка – вверх.
Надеемся, что у вас получился слон на счастье! Дорисуйте ему глаз и хвост.
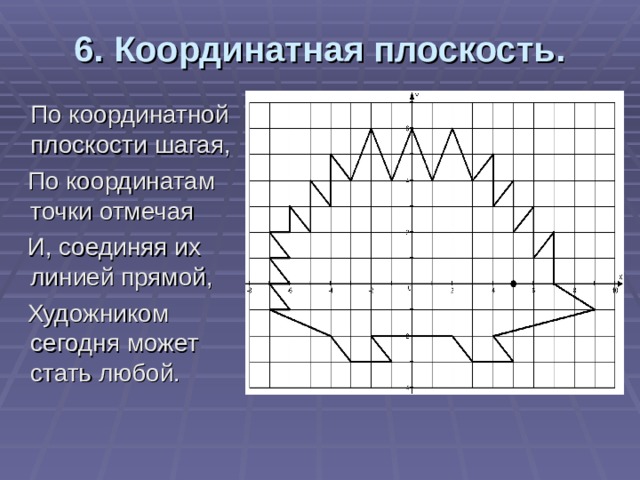
6. Координатная плоскость.
В этом году, когда мы познакомились с координатной плоскостью, то убедились, что без клеток на математике точно никуда! При их помощи и названных координат мы все становились художниками…
По координатной плоскости шагая,
По координатам точки отмечая
И, соединяя их линией прямой,
Художником сегодня может стать любой.
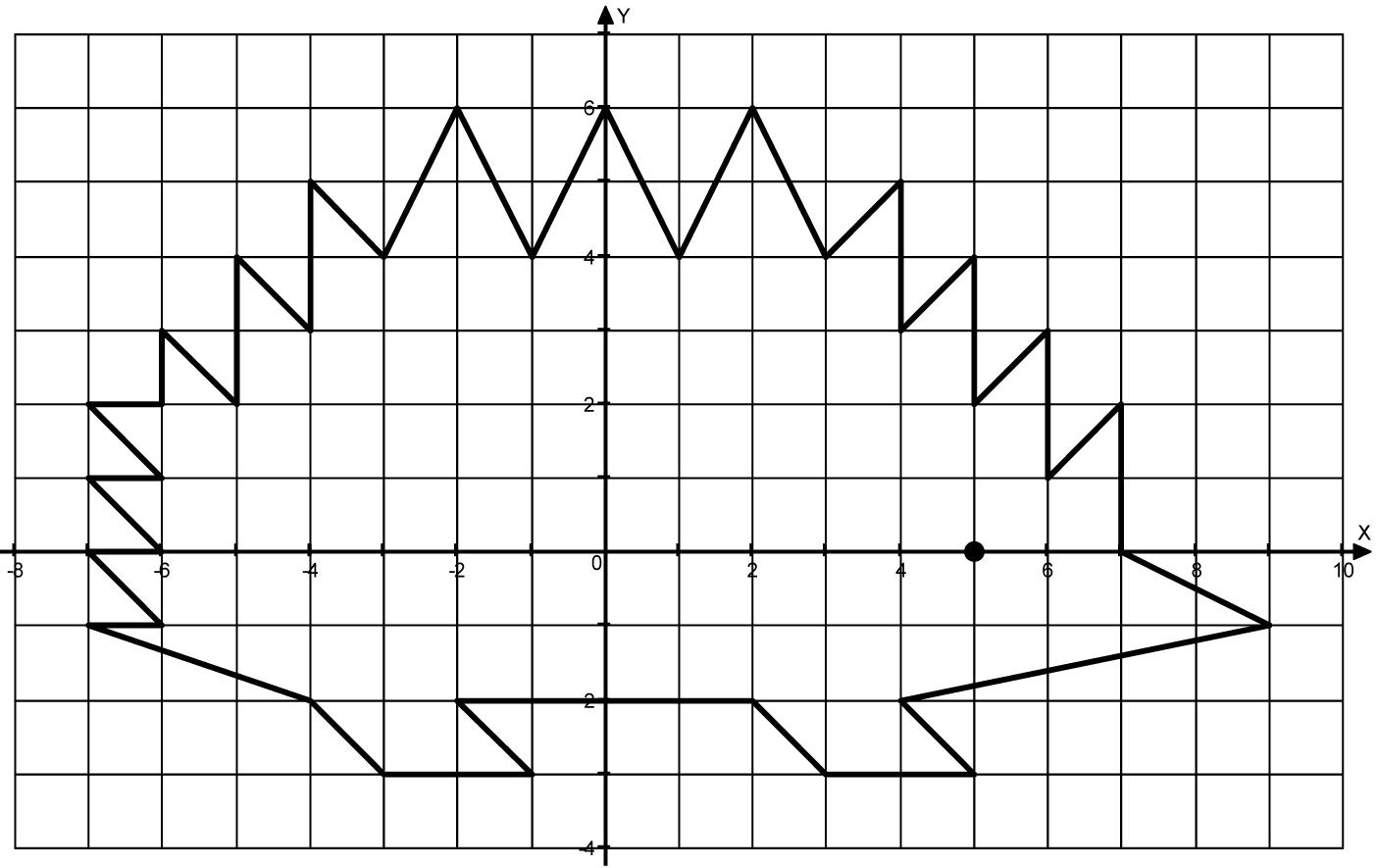
Это пока всё, что мы успели записать, но думаем, что со временем сможем открыть и другие волшебные свойства клетчатой бумаги. А пока подведём наши итоги.
Заключение.
Узлы клеток превращают чистый лист бумаги в волшебную страну.
Они, как звёзды на небе открывают нам созвездия геометрических фигур
и их свойства. Они помогают строить и измерять. Они создают удивительные художественные образы и приобщают к искусству.
Таким образом, обычная тетрадь по математике вовсе не обычная. Клетка позволяет ей совершать настоящие чудеса!
Литература.
1. http://economka.kz/publ/kontrolnaja_zakupka_2/kanceljarskie_tovary/tetrad_shkolnaja_v_kletku/35-1-0-234
2. http://aleks-6zklass.narod.ru/p11aa1.html
3. И.Ф. Шарыгин, Л.Н. Ерганжиева «Наглядная геометрия»: учебное пособие для 5-6 классов – Смоленск: Русич,1995
- 13 -










 ешение. По формуле Пика:
ешение. По формуле Пика:  ешение. По формуле Пика:
ешение. По формуле Пика:  ешение. По формуле Пика:
ешение. По формуле Пика:  ешение. По формуле Пика:
ешение. По формуле Пика: