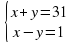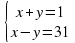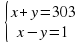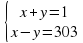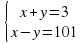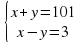25
Муниципальное бюджетное общеобразовательное учреждение
«Хвощевская школа»
Исследовательская работа
Делимость и остатки

Выполнил:
Кициев Александр Владимирович
7 класс
Руководитель:
Колесова Ольга Викторовна
учитель математики
высшей категории
с. Хвощевка
2017г.
Содержание
Введение……………………………………………………..……….…3
Основная теорема арифметики……………………………….……….4
Важные определения ……………………………………………….....7
Остатки…………………………………………………………………..9
Алгоритм Евклида……………………………………………………..14
Заключение………………………………………………………….…16
Список Интернет-ресурсов………………………………………...…17
Приложение 1…………………………………………………...……..18
Приложение 2………………………………………...………………..22
Введение
Арифметика – это наука о числах, с которой любой человек начинает знакомство с увлекательным миром математики. Как говорил М. В. Ломоносов, арифметика – это врата учености, открывающие нам путь к миропознанию. А ведь он прав, разве познание мира можно отделить от знания цифр и букв, математики и речи? Возможно, в былые времена, но не в современном мире, где бурное развитие науки и техники диктует свои законы
Слово "арифметика" (греч. "арифмос") греческого происхождения, обозначает "число". Она изучает число и все что может быть с ними связано. Это мир чисел: различные действия над числами, числовые правила, решение задач, которые связаны с умножением, вычитанием и т. д.
Цель исследовательской работы: углубить и расширить знания по теме "Делимость и остатки»
Задачи:
Рассмотреть основную теорему арифметики и её практическое применение;
Изучить решения задач на остатки методом перебора;
Научится применять алгоритм Евклида для нахождения НОД и НОК;
Познакомить одноклассников со своими исследованиями.
Проблемный вопрос: Как применяется для решения олимпиадных задач основная теорема арифметики, делимость остатков, алгоритм Евклида?
Методы исследовательской работы:
Сбор и структурирование собранного материала на различных этапах исследования.
Метод анализа, синтеза, обобщения и сравнения.
Практическое применение.
Основная теорема арифметики
Среди натуральных чисел есть простые и составные. Число является составным, если оно равно произведению двух меньших натуральных (например, 6 = 2 • 3). В противном случае число (если оно, кроме того, отлично от 1) называется простым. Единица не является ни простым, ни составным числом.
Простые числа являются своего рода "кирпичиками", из которых можно построить все остальные числа. В каком же смысле? Например, чисто 420, без сомнения, составное. Его можно разложить на множители: 420 = 42 • 10. Каждое из чисел 42 и 10 также составное: 42 = 6 • 7, 10 = 2 • 5.
Поскольку 6 = 2 • 3,
то 420 = 42 • 10 = 6 • 7 • 2 • 5 = 2 • 3 • 7 • 2 • 5 = 2 • 2 • 3 • 5 • 7. Получаю разложение нашего числа на простые сомножители.
Таким же образом, можно представить в виде произведения простых чисел любое натуральное число (кроме 1) - надо раскладывать получающиеся сомножители в произведение меньших, пока это удается. А что, если попробовать разложить число 420 на множители по-другому? Например, начав так: 420 = 15 • 28. Получается то же самое разложение
420 = 15 • 28 = 3 • 5 • 4 • 7 = 3 • 5 • 2 • 2 • 7= 2 • 2 • 3 • 5 • 7.
Делаю вывод - каждое натуральное число, за исключением единицы, раскладывается в произведение простых сомножителей, причем единственным образом. Это утверждение называется ОСНОВНОЙ ТЕОРЕМОЙ АРИФМЕТИКИ.
Рассмотрим примеры применения теоремы
1. Делится ли 29 • 3 на 2?
Ответ: Да, так как 2 входит в разложение этого числа на простые множители.
2. Делится ли 29 • 3 на 5?
Ответ: Нет, потому что в разложении этого числа на простые множители нет простого числа 5.
3. Делится ли 29 • 3 на 8?
Ответ: Да, поскольку 8 = 23, а в разложение данного числа на простые множители двойка входит 9 раз
4.Делится ли 29 • 3 на 9?
Ответ: Нет, так как в разложение данного числа на простые множители тройка входит лишь один раз, а в разложение числа 9 – дважды.
5. Делится ли 29 • 3 на 6?
Ответ: Да, потому что 6 = 2•3, а2иЗ входят в разложение данного числа на простые.
6. Верно ли, что если натуральное число делится на 4 и на 3, то оно делится
на 12?
Ответ: Да. В разложение на простые множители числа, делящегося на 4, двойка входит по крайней мере 2 раза. Поскольку число делится и на 3, то в его разложение входит и тройка. Поэтому оно делится на 12.
7. Верно ли, что если натуральное число делится на 4 и на 6, то оно делится
на 24 = 4 • 6?
Ответ: Нет. Например, число 12. Дело в том, что если число делится на 4, то в его разложение на простые множители по крайней мере дважды входит число 2; из делимости числа на 6 следует, что в его разложении есть 2 и 3. Таким образом, заведомо в это разложение входят две (не три!) двойки и одна тройка, и можно утверждать лишь то, что число делится на 12.
8. Число А не делится на 3. Может ли на 3 делиться число 2А?
Ответ: Нет, поскольку тройка не входит в разложение на простые множители числа 2А.
9. Число А - четно. Верно ли, что ЗА делится на 6?
Ответ: Да, так как 2 и 3 входят в разложение числа ЗА на простые множители.
10. Число 5А делится на 3. Верно ли, что А делится на 3?
Ответ: Да, потому что в разложение числа 5А на простые множители тройка входит, а в разложение числа 5 - нет.
11. Число 15А делится на 6. Верно ли, что А делится на 6?
Ответ: Нет. Например, А = 2. Дело в том, что тройка, входящая в разложение числа 6, входит и в разложение числа 15. Поэтому можно утверждать лишь то, что в разложении числа А обязательно есть двойка.
Важные определения
Первое. Два числа называются взаимно простыми, если у них нет общих делителей, отличных от единицы.
Так, например, два разных простых числа, конечно, являются взаимно простыми. Используя рассуждения, подобные тем, которые приведены в ответах на вопросы 6 и 10, можно доказать два следующих факта:
а) Если некоторое число делится на два взаимно простых числа п и т , то оно делится и на их произведение пт.
б) Если число рА делится на q, где р и q взаимно просты, то и А делится на q.
Второе. Наибольшим общим делителем (для краткости НОД) двух чисел называется наибольший из общих делителей этих чисел.
Третье. Наименьшим общим кратным (НОК) двух чисел называется наименьшее число, делящееся на каждое из них.
Так, например, НОД(18,24) = 6, НОК(18,24) = 72.
Дополним список примеров еще двумя.
А = 23 • З10 • 5 • 72, В = 25 • 3 • 11. Чему равен НОД(А,В)? Ответ: 24 = 23 • 3. Это - общая часть разложений.
А = 28 • 53 • 7, В = 25 • 3 • 57. Чему равен НОК(А.В)?
Ответ: 420000000 = 28 • 3 • 57 • 7. Это - объединение разложений.
Решение подобных задач смотри в приложении 1:
Задача 1. pи q - различные простые числа. Сколько делителей у числа:
a) pq; б) p2q; в) p2q2; г) pnqm?
Задача 2. Докажите, что произведение любых трех последовательных натуральных чисел делится на 6.
Задача 3. Докажите, что произведение любых пяти последовательных чисел делится: а) на 30; б) на 120.
Задача 4. р - простое число. Сколько существует натуральных чисел:
а) меньших р и взаимно простых с ним; б) меньших р2 и взаимно простых с ним?
Задача 5. Каково наименьшее натуральное п, такое, что п! делится на 990?
Задача 6. Может ли n! оканчиваться ровно на 5 нулей?
Задача 7. На сколько нулей оканчивается число 100! ?
Задача 8. Докажите, что число, имеющее нечетное число делителей, - точный квадрат.
Задача 9. Вася написал на доске пример на умножение двух двузначных чисел, а затем заменил в нем все цифры на буквы, причем одинаковые цифры - на одинаковые буквы, а разные - на разные. В итоге у него получилось АВВГ=ДДБЕ. Докажите, что он где-то ошибся.
Задача 10. Может ли число, записываемое при помощи 100 нулей, 100 единиц и 100 двоек, быть точным квадратом?
Задача 11. 56а = 65b. Докажите, что a+b - составное число.
Задача 12. Решите в натуральных числах уравнения:
а) х2 — у2 = 31; б) х2 — у2 = 303.
Задача 13. Решите в уравнение х3 + х2 + х — 3 = 0 в целых числах
Задача 14. Докажите, что для любых натуральных чисел а и b верно равенство НОД(а,b)НОК(а,b) = аb.
Остатки
Предположим, что нужно разделить 20 на 3. Запишем: 20 = 6 • 3 + 2. Это запись деления 20 на 3 с остатком. Ясно, что при делении на 3 остатком может быть любое из трех чисел: 0, 1,2. Остаток равен нулю, если исходное число делится на 3 нацело.
Определение: Разделить натуральное число N на натуральное число m с остатком означает представить N в виде N = km+r, где 0 r При этом число г называется остатком от деления N на т.
Решим задачу: найти остаток от деления числа 22 • 50 + 44 • 10 на 3. Для этого не обязательно вычислять выписанное выражение. Поступим так: заменим каждое из чисел на его остаток от деления на 3. Получим выражение 1 • 2 + 2 • 1. Это число равно 4 и дает остаток 1 при делении на 3. Мы утверждаем, что остаток исходного выражения от деления на 3 также равен 1. Дело в том, что верны следующие утверждения:
Сумма любых двух натуральных чисел и сумма их остатков имеют одинаковые остатки при делении на 3.
Произведение любых двух натуральных чисел и произведение их остатков имеют одинаковые остатки при делении на 3.
Задача 1. Найдите остатки от деления
а) 1990 • 1991 • 1992 + 19933 на 7;
б) 9100 на 8.
Решение:
Произведение (сумма) двух целых чисел даёт такой же остаток при делении на n, как и произведение (сумма) их остатков при делении на n.
а) Данное выражение даёт при делении на 7 такой же остаток, как и 2·3·4 + 52= 49.(1990:7= 284 ост.2, 1991:7= 284 ост.3, 1992:7= 284 ост.4, 1993:7= 284 ост.5) 49 делится на 7 остаток 0
б) Данное выражение даёт при делении на 8 такой же остаток, как и 1100= 1.
Ответ: а) 0; б) 1.
Решение следующей задачи содержит очень важную идею.
Задача 2. Докажите, что п3 + 2п делится на 3 для любого натурального п. Решение: Число п может давать при делении на 3 один из трех остатков: 0,1,2. Рассмотрим три случая.
Если п дает остаток 0, то и п 3 и 2п делятся на 3 и поэтому п 3 + 2п также делится на 3.
Если п дает остаток 1, то п 3 дает остаток 1, 2п - остаток 2, а 1 + 2 делится на 3.
Если п дает остаток 2, то п2 дает остаток 1, п 3 - остаток 2, 2п - остаток 1, а 2 + 1 делится на 3.
Требуемое доказано.
Задача 3. Докажите, что п5 + 4n делится на 5 при любом натуральном п.
Задача 4. Докажите, что п2 + 1 не делится на 3 ни при каком натуральном п.
Задача 5. Докажите, что п 3 + 2 не делится на 9 ни при каком натуральном п.
Задача 6. Докажите, что п3 — п делится на 24 при любом нечетном п.
Задача 7. а) Докажите, что р2 — 1 делится на 24, если р - простое число и
р3.
б) Докажите, что р2 —q2 делится на 24, если р и q - простые числа,
большие 3.
Задача 8. Натуральные числа х, у, z таковы, что х2 + у2 = z2. Докажите, что хотя бы одно из этих чисел делится на 3.
Задача 9. Докажите, что сумма квадратов трех натуральных чисел-, уменьшенная на 7, не делится на 8.
Перейдем к следующему циклу задач:
Задача 10. Найдите последнюю цифру числа 19891989.
Решение: Заметим сначала, что последняя цифра числа 19891989 совпадает с последней цифрой числа 91989. Выпишем последние цифры нескольких начальных степеней числа 9: 9, 1, 9, 1, 9, ....
Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 - 9 (1 • 9 = 9).
Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 19891989 - девятка.
Задача 11. Найдите последнюю цифру числа 250.
Решение: Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2,Видим, что 25 также, как и 21, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет "зацикливание": 26 (как и 22) оканчивается на 4, 27 (как и 23) - на 8, 28 - на 6, 29 - на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 250 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 250 совпадает с последней цифрой числа 22, то есть равна 4.
Задача 12. Найдите остаток от деления 2100 на 3.
Задача 13. Найдите остаток от деления З1989 на 7.
Задача 14 Докажите, что 2222555S + 55 552222 делится на 7.
Задача 15. р и р2 + 2 - простые числа. Докажите, что р3 + 2 - также простое число.
Задача 16. Докажите, что а3 + Ь3 + 4 не является кубом целого числа ни при каких натуральных а и Ь.
Задача 17. Докажите, что число 6п3 + 3 не является шестой степенью целого числа ни при каком натуральном п.
Решение задач смотри в приложении 2
Рассмотрим ещё несколько задач не объединенных какой-либо идеей или методом решения.
Задача 18. а) а + 1 делится на 3. Докажите, что 4 + 7а делится на 3.
Решение
7а + 4 = 7(а + 1) - 3 , т.к. a+1 делится на 3 и 3 делится на 3, то и их разность 7(а + 1) - 3 делится на 3.
б) 2 + а и 35 - b делятся на 11. Докажите, что делится на 11.
Решение
б) a + b= (2 +a) – (35 –b) + 33. Каждое из слагаемых делится на 11, значит и вся сумма a + b делится на 11.
Задача 19. Найдите последнюю цифру числа 12 + 22 + ... + 992.
Решение
12+ 22+ ... + 992≡ 10(12+ 22+ ... + 92) = 0 (mod 10).
Задача 20. Докажите, что сумма п последовательных нечетных натуральных чисел при п 1 является составным числом.
Решение
Если n чётно, то сумма тоже чётна (и больше 2).
Если же n нечётно, то сумма делится на среднее из наших чисел: сумма первого и последнего (второго и предпоследнего, и т.д.) в два раза больше среднего числа. Значит сумма является составным числом.
Задача 21. Найдите наименьшее число, дающее следующие остатки: 1 - при делении на 2, 2 - при делении на 3, 3 - при делении на 4, 4 - при делении на 5, 5 - при делении на 6.
Заметим, что это число, увеличенное на 1, делится на 2, 3, 4, 5, 6.
НОК(2, 3, 4, 5, 6) – 1 =59.
Ответ: 59
Задача 22. Докажите, что если (п — 1)! + 1 делится на п, то п - простое число.
Решение
Пусть n+ 1 – составное число. Если p – некоторый его простой делитель, то p ≤ n. Значит, n! делится на p, а n! + 1 не делится. Противоречие.
Отдельно рассмотрим следующие две задачи:
Задача 23! Докажите, что существует такое натуральное п, что числа п + 1, п + 2, ..., п + 1989 - составные.
Решение:
Попробуем рассказать, как пойти по самому простому пути: сделаем так, чтобы п + 1 делилось на 2. п + 2 также должно быть составным, но делиться на 2 уже не может. Попытаемся опять пойти по самому простому пути: хотелось бы сделать так, чтобы п + 2 делилось на 3. Продолжая в том же духе, можно пытаться найти число п такое, что п+1 делится на 2, п + 2 - на 3, п + 3 - на 4 и так далее. Это равносильно тому, что п - 1 делится на 2, 3, 4, ..., 1990. Такое число, конечно, существует - например, 1990!. Итак, в качестве искомого п можно взять число 1990! + 1.
Задача 24! Докажите, что существует бесконечно много простых чисел.
Решение: Предположим противное. Пусть р1, р2,… р п - все простые числа. Рассмотрим число р1р2…р п + 1. Это число не делится ни на одно из чисел р1, р2,… р п и, следовательно, не может быть разложено в произведение простых. Противоречие.
.
Алгоритм Евклида
На уроках мы обсудили понятие наибольшего общего делителя двух натуральных чисел и выяснили, как его можно найти: достаточно выписать разложения этих чисел на простые множители и взять их общую часть. Однако для больших чисел эта процедура практически неосуществима. Например, таким способом найти наибольший общий делитель чисел 1381955 и 690713 очень сложно, так как трудно подобрать простые делители.
| 1381955 | 5 |
| 690713 | 23 |
| 276391 | 23 |
| 30031 | 59 |
| 12017 | 61 |
| 509 | 509 |
| 197 | 197 |
| 0 |
|
| 0 |
|
| |
|
НОД(1381955; 690713) = 23
Рассмотрим другой метод, позволяющий вычислить НОД двух чисел. Он называется алгоритмом Евклида.
Алгоритм Евклида основан на следующем простом соображении: любой общий делитель чисел а и b (а b) делит также число а — b; кроме того, любой общий делитель чисел b и а— b делит число а. Тем самым,
НОД(а, b) = НОД(b,а- b).
Покажем, как работает алгоритм Евклида для конкретных чисел. Найдем наибольший общий делитель чисел 451 и 287:
НОД(451,287) = НОД(287,164) = НОД(164,123) = НОД(123,41) =НОД(82,41)= = НОД(41,41) = 41.
Заметим, что алгоритм Евклида можно ускорить: заменять а не на а - b, а сразу на остаток от деления а на b. Продемонстрируем это на примере наших чисел:
НОД(1381955,690713) = НОД(690713,529) =
= НОД(529,368) =
= НОД(368,161) =
= НОД(161,46) =
= НОД(46,23) =
= НОД(23,0) =
= 23.
Как видно, этот метод очень быстро приводит к результату.
Задача 1. Найти наибольший общий делитель чисел 2п + 13 и п + 7.
Решение
НОД(2 п + 13, п + 7) = НОД(п + 7, п + 6) = НОД(п + 6,1) = 1.
Задача 2. Докажите, что дробь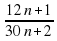 - несократима ни при каком натуральном п.
- несократима ни при каком натуральном п.
Решение
НОД(30n+ 2, 12n+ 1) = НОД(12n+ 1, 18n+ 1) =НОД(18n+ 1,12n+ 1) = =НОД(12n+ 1, 6n) = НОД(6n, 1) = 1.
Задача 3. Найдите НОД(111...111, 11... 11) - в записи первого числа 100 единиц, в записи второго — 60.
Решение
НОД(111...111, 11... 11)= НОД(11...11, 1... 1)= НОД(1...1, 1...1)=





 100 60 60 40 40 20
100 60 60 40 40 20


 = НОД(1...1, 1...1)= 1...1
= НОД(1...1, 1...1)= 1...1
20 20 20
Ответ:1…1 – 20единиц
Заключение
Результаты исследования заключаются в том, что данная работа выходит за рамки школьной программы. Ровесники и старшеклассники не знают о существовании основной теоремы арифметики и алгоритме Евклида для нахождения НОД и НОК, что подтверждается результатами анкетирования. ![]()
А, ведь знание их значительно упрощает процесс многих вычислений, экономит время, позволяет решать олимпиадные задачи. С решениями некоторых задач на применение основной теоремы арифметики, нахождения остатков, применения алгоритма Евклида для нахождения НОК и НОД своей работы я ознакомил старшеклассников, которые хотят получить высокие баллы на экзаменах по математике. Собранный мной материал можно использовать на уроках математики, на занятиях математического кружка.
Цель работы достигнута, задачи реализованы.
Список литературы и Интернет-ресурсов
Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математические кружки Киров: "АСА" 1994
http://fb.ru/article/202586/chto-takoe-arifmetika-osnovnaya-teorema-arifmetiki-dvoichnaya-arifmetika
http://www.problems.ru/view_by_source_
https://docviewer.yandex.ru/?url=http%3A%2F%2Fmathus.ru%2Fmath%2Fostear.pdf&name=ostear.pdf&lang=ru&c=589c0e534770
http://www.cleverstudents.ru/divisibility/nod_finding.html
Приложение 1
Решения задач раздела «Важные определения»
Задача 1. pи q - различные простые числа. Сколько делителей у числа:
a) pq; б) p2q; в) p2q2; г) pnqm?
Решение
а) p и q простые числа, которые делятся на 1 и на самих себя, поэтому pq делится на 1, на p, на q и на pq (4 делителя)
б) p²q делится на 1, p, p², q, pq, p²q (6 делителей)
в) p²q² делится на 1, p, p², q, q², pq, p²q, pq², p²q² (9 делителей)
г) pnqm делится на 1, p, p², .., pn (n+1 делителей) и
делится на 1, q, q2, q3,…, qm (m+1 делителей). Всего делителей (n+1) • (m+1).
Ответ: а) 4, б) 9, в) n+1, г) (n+1) • (m+1).
Задача 2. Докажите, что произведение любых трех последовательных натуральных чисел делится на 6.
Решение
Среди этих трёх чисел есть хотя бы одно чётное число. Значит, в разложении произведения на простые множители есть множитель 2. Среди этих трёх чисел одно число делится на 3. Значит, в разложении произведения на простые множители есть множитель 3. В разложении произведения на простые множители есть простые числа 2 и 3. Значит, оно делится на их произведение, то есть на 6.
Если же из этих трёх чисел чётное число само и является кратным 3, то это число автоматически делится на 6, поскольку оно кратно и 2 и 3 одновременно. Произведение такого числа на два рядом стоящих тоже будет кратно 6.
Задача 3. Докажите, что произведение любых пяти последовательных чисел делится: а) на 30; б) на 120.
Решение
а) Среди этих чисел есть число, кратное 3, есть число, кратное 5, и есть чётное число. Значит, произведение делится на произведение простых чисел 2, 3, 5, то есть на 30.
б) Среди пяти подряд идущих чисел есть два чётных, одно из которых делится на 4. Поэтому, в разложении произведения на простые множители число 2 встретится трижды. Значит, произведение делится на 3, 5 и 8, то есть и на их произведение 120.
Задача 4. р - простое число. Сколько существует натуральных чисел:
а) меньших р и взаимно простых с ним; б) меньших р2 и взаимно простых с ним?
Например. Заметим, что 849 = 292 и 29 – простое число. Теперь нетрудно сообразить, что существует 29(29 - 1) = 812 натуральных чисел, которые не превосходят число 841 и не имеют с ним общих делителей, отличных от 1.
Ответ: а) p–1; б) p²– p.
Задача 5. Каково наименьшее натуральное п, такое, что п! делится на 990?
Решение
990 =2• 3•3•5•11
Поскольку в разложение числа 990 на простые множители входит число 11, то n≥ 11. С другой стороны, n= 11 удовлетворяет условию задачи. Это легко проверить 11!= 1•2•3•4•5•6•7•8•9•10•11= (2•5•9•11) •(1•3•4•6•7•8•10)
Ответ: n= 11.
Задача 6. Может ли n! оканчиваться ровно на 5 нулей?
Решение
24!=1•2•3•4•5•6•7•8•9•10•11•12•13•14•15•16•17•18•19•20•21•22•23•24 оканчивается на четыре нуля (2•5; 10; 12•15; 20). При добавлении множителя 25 добавится еще два нуля (так как число 25 в разложение факториала добавит сразу две пятерки, а именно, 25•4). Поэтому 25! оканчивается уже на шесть нулей.
Ответ: не может.
Задача 7. На сколько нулей оканчивается число 100! ?
Решение
В образовании нулей участвуют числа, кратные 2 и 5. Четных чисел больше, так что их не считаем. А чисел, кратных 5 от 1 до 100 - 20 штук. И еще 4 числа, кратных 25. Значит, нулей в результате будет 24.
Ответ: 24
Задача 8. Докажите, что число, имеющее нечетное число делителей, - точный квадрат.
Подсказка
Если d - делитель числа n, то n/d – также делитель.
Решение
Если d - делитель числа n, то n/d – также делитель. Таким образом, все делители числа делятся на пары. Если число имеет нечётное число делителей, то делители какой-то пары совпадают. Тогда d = n/d, откуда n=d2, то есть число n – квадрат целого числа.
Из решения ясно, что нечётное число делителей имеют точные квадраты и только они.
Задача 9. Вася написал на доске пример на умножение двух двузначных чисел, а затем заменил в нем все цифры на буквы, причем одинаковые цифры - на одинаковые буквы, а разные - на разные. В итоге у него получилось АВВГ=ДДБЕ. Докажите, что он где-то ошибся.
Подсказка
Рассмотрите делимость на 11.
Решение
Результат умножения (число справа) делится на 11. Значит, на 11 делится один из множителей. Двухзначное число кратно 11, если равны его цифры. Но по условию A ≠ Б, В ≠ Г, что противоречит условию.
Задача 10. Может ли число, записываемое при помощи 100 нулей, 100 единиц и 100 двоек, быть точным квадратом?
Подсказка
Рассмотрите делимость на 3.
Решение
Согласно признаку делимости, такое число кратно 3. Если бы оно было полным квадратом, то делилось бы на 9. Но число не кратно 9 (сумма его цифр – 300 –не кратна 9).
Ответ: не может.
Задача 11. 56а = 65b. Докажите, что a+b - составное число.
Подсказка
Выразите a + b через a.
Решение
65(a + b) = 65a + 65b = 65a + 56a = 121a. Так как числа 65 и 121 взаимно просты, то a + b делится на 121. Поскольку 121 - составное число, то и a + b – составное.
Задача 12. Решите в натуральных числах уравнения:
а) х2 — у2 = 31; б) х2 — у2 = 303.
Решение
а) х2 — у2 = 31
(x +y) • (x-y) =31•1Получаем две системы:
| 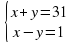
2х=32 х=16 у=31-16=15 | 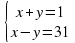
2х=32 х=16 у=1-16=-15 не удовлетворяет условию задачи |
Ответ: х=16, у=15
б) х2 — у2 = 303 303= 1•303 = 3•101
Получаем четыре системы:
| 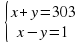
2х=304 х=152 у=303-152=151 | 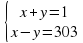
2х=304 х=152 у=1-152=-151 не является натуральным числом | 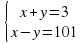
2х=104 х=52 у=3-52=49 не является натуральным числом | 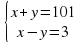
2х=104 х=52 у=101-52=49 |
Ответ: х=152, у=151 или х=52, у=49
Задача 13. Решите в уравнение х3 + х2 + х — 3 = 0 в целых числах
Решение
х3 + х2 + х — 3 = 0
х ( х2 + х+1)=3
Значит х=±3или х=±1 Проверяем х=1
Ответ: х=1
Задача 14. Докажите, что для любых натуральных чисел а и b верно равенство НОД(а,b)НОК(а,b) = аb.
Решение
Из определения НОД следует, что a = a' НОД(a, b), b = b' НОД(a, b), где НОД(a', b') = 1. Из определения НОК следует, что
НОК(a, b) = a' b' НОД(a, b). Поэтому
НОД(a, b)НОК(a, b) =a' b'НОД(a, b)НОД(a, b) = ab.
Приложение 2
Решения задач раздела «Остатки»
Задача 3. 1) Докажите, что n5+4n делится на 5 при любом натуральном n.
Решение
n5+4n = n(n4+4) = n((n2)2+4)
Если n делится на 5, то и n5+4n = n(n4+4) тоже делится на 5.
Пусть n не делится на 5. Тогда n2оканчивается одной из цифр 1, 4, 6, 9,
а (n2)2оканчивается либо 1, либо 6,
поэтому (n4+4) оканчивается либо 5, либо 0, значит, делится на 5.
Задача 4. Докажите, что п2 + 1 не делится на 3 ни при каком натуральном п.
Решение
Случай, когда n делится на 3, очевиден, п2 + 1 не делится на 3 ни при каком натуральном п.
Если же не n делится на 3, то на 3 делится число n2– 1=(n–1)(n+1), поскольку одно из чисел n– 1, n+ 1 делится на 3. Следовательно, в этом случае
n2+ 1 ≡ 2 (mod 3).
Задача 5. Докажите, что п 3 + 2 не делится на 9 ни при каком натуральном п.
Решение
Случай, когда n делится на 3, очевиден. Если же не n делится на 3, то n= 3k ± 1 и n3 = (3k ± 1)3 = 27k3± 27k2+ 9k± 1 ≡ ± 1 (mod 9).
Задача 6. Докажите, что п3 — п делится на 24 при любом нечетном п.
Подсказка
Докажите, что указанное число делится и на 3, и на 8.
Решение
n3–n= n (n– 1)(n+ 1). Из трёх последовательных чисел одно делится на 3.
n– 1 и n+ 1 – последовательные чётные числа. Поэтому одно из них не только чётно, но и делится на 4. Значит, всё произведение делится на 2·4·3 = 24.
Задача 7.
а) Докажите, что p²–1 делится на 24, если p – простое число и p3
Решение
p²–1= (р - 1)(р + 1). Т.к. p – простое число и p3, то р – нечетное число. Известно, что среди трех последовательных чисел всегда найдется число кратное 3 и 4 (например, 6, 7, 8), если среднее число нечетно. Рассмотрим три последовательных числа р – 1, р, р + 1. р – нечетное число, значит, р – 1 и р + 1 – четные числа. р не кратно 3, значит, либо р – 1, либо р + 1 кратно 3, а так как оно четное, то кратно 6, другое число кратно 4, тогда произведение
(р - 1)(р + 1) кратно 24.
б) Докажите, что р2 —q2 делится на 24, если р и q - простые числа, большие 3.
Решение
p2–q2= (p–q)(p+q). p – q и p + q – чётные числа, причём их разность 2q не кратна 4. Значит, одно из этих чисел делится на 4. 2q также не кратно 3, значит, p – q и p + q дают разные остатки при делении на 3. Если бы ни одно из этих чисел не было кратно 3, то сумма (p – q) + (p + q) = 2p делилась бы на 3. Но это не так. Поэтому (p – q)(p + q) делится на 2·4·3 = 24.
Задача 8. Натуральные числа х, у, z таковы, что х2 + у2 = z2. Докажите, что хотя бы одно из этих чисел делится на 3.
Решение
Если ни x, ни y не делятся на 3, то x2 и y2 дают остаток 1 при делении на 3 (см. решение задачи 4). Таким образом, их сумма имеет остаток 2 при делении на 3. Но z2не может иметь такого остатка. Значит наше предположение не верно, и либо x, либо y делится на 3
Задача 9. Докажите, что сумма квадратов трех натуральных чисел-, уменьшенная на 7, не делится на 8.
Подсказка
Выясните возможные остатки квадратов при делении на 8.
Решение
Квадрат при делении на 8 может дать остаток 0, 1 или 4. Число 7 нельзя представить как сумму трёх таких слагаемых.
Задача 12. Найдите остаток от деления 2100 на 3.
Решение
При делении любого числа (не кратного 3) на 3 получаются остатки 1 или 2.
Рассмотрим степени 2 и остатки при делении на 3
21=2
22=4 ост 1
23=8 ост 2
24=16_ ост 1
25=32 ост 2
26=64 ост 1
27=128 ост 2
28=256 ост 1
29=512 ост 2 т.е. у четных степеней ост 1, а у нечетных ост 2
и т.д. 2100 =…6 ост 1
Ответ: Ост. 1
Задача 13. Найдите остаток от деления З1989 на 7.
Решение
31989 = 27663 ≡ (–1)663 = –1 (mod 7).
Ответ: 6.
Задача 14. Докажите, что 2222555S + 55 552222 делится на 7.
Решение
5555 ≡ 4 (mod 7). Заметим, что 43≡ 1 (mod 7), значит, 22225555+ 55552222≡ 22225555+ 55555555, а это число делится на 2222 + 5555 = 7777.
Задача 15. р и р2 + 2 - простые числа. Докажите, что р3 + 2 - также простое число.
Подсказка
Рассмотрите остатки от деления на 3.
Решение
Если число p делится на 3 и больше 3, то оно не простое. Пусть p не делится на 3 и больше 1. Тогда p2 даёт остаток 1 от деления на 3, то есть p2+2 делится на 3. Поскольку p2+ 2 3, то это число – составное. Остаётся единственная возможность p= 3. При этом p3+ 2 = 29.
Задача 16. Докажите, что а3 + Ь3 + 4 не является кубом целого числа ни при каких натуральных а и Ь.
Подсказка
Выясните, какой остаток может давать число a3+b3+ 4 от деления на 9.
Решение
Куб может давать только остатки 0 или ±1 при делении на 9. Поэтому a3+b3+4 имеет остаток 0, 2, 3, 5 или 6, что не совпадает с остатками кубов.
Задача 17. Докажите, что число 6п3 + 3 не является шестой степенью целого числа ни при каком натуральном п.
Подсказка
Выясните, какой остаток может давать число 6n3+ 3 от деления на 7.
Решение
Куб может давать только остатки 0 или ±1 при делении на 7, а шестая степень – только остатки 0 и 1. 6n3+ 3 ≡ 3 –n3≡ 3, 2 или 4 (mod 7).










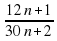 - несократима ни при каком натуральном п.
- несократима ни при каком натуральном п.




 100 60 60 40 40 20
100 60 60 40 40 20