Исследовательская работа "Искусство + математика = орнамент"

Федеральное государственное бюджетное образовательное учреждение высшего образования «Казанский национальный исследовательский технологический университет

Номинация « математика»

Исследовательская работа

Прикладные вопросы математики

«Искусство + математика = ОРНАМЕНТ»

г. Казань, 2017

ОГЛАВЛЕНИЕ

Введение________________________________________3 стр.

Цель работы ____________________________________4 стр.

Биография М.К. Эшера_________________________5стр.

Эти необыкновенные паркеты___________________6-9 стр.

Фотографии паркета (наша работа)_______________10-12 стр.

Заключение__________________________________ 13 стр.

Список литературы____________________________14 стр

For me it remains an open question whether [this work]
pertains to the realm of mathematics or to that of art.

         M.C. Escher

Для меня остается открытым вопрос о том, [ эта работа ]

относится к области математики или искусства

М. К. Эшер

Введение.

Однажды в руки мне попался старый номер журнала «Квант», я обратил внимание на рисунок, размещенный на обложке. Это был куб с полосками. Выступы на лентах являются визуальным ориентиром того, как расположены полоски в пространстве и как они переплетаются с кубом. И если вы верите своим глазам, то вы никогда не поверите тому, что нарисовано на этой картине. Просматривая другие номера журнала, я обнаружил, что и на обложках других номеров присутствуют рисунки с изображением пространственных фигур, с различным способом их моделирования. Мне стало интересно: кто создал эти рисунки, какой математик? Мне казалось, что только математик, знающий правила преобразований, способен нарисовать эти необычные, фантастические картины. Каково же было наше удивление, когда я узнал автора иллюзий: Морис Корнелис Эшер (Maurits Cornelis Escher; 1898—1972). Так же я узнал, что сам Эшер плохо знал математику. Однажды известный геометр Г. Кокстер пригласил Эшера на свою лекцию, посвященную математическому содержанию его гравюр и литографий. К взаимному разочарованию, Эшер не понял почти ни слова из того, о чем рассказывал Кокстер. Вот что писал об этом сам художник:

«Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен».

Цель работы: Показать связь фантастического творчества Эшера с прикладной математикой.

Задачи исследования:

1. изучить творчество Эшера и определить математическую составляющую его творчества;

2. подготовить виртуальную экскурсию в музей картин Эшера, усовершенствуя навыки в работе с информационно-коммуникативными технологиями;

3. осуществить межпредметные связи математики, изобразительного искусства, информатики, истории.

Методы исследования: поиск информации, сравнения, классификация, анализ, обобщение.

Основополагающий вопрос: Как связано творчество Мориса Эшера с математикой?

Объект исследования: творчество Эшера (паркеты)

Гипотеза: творчество Эшера тесно связано с геометрией, как на плоскости, так и в пространстве, что придает его работам фантастичность и необычность

Ожидаемые результаты:

Показать все красоту и прелесть картин Мориса Эшера с математической точки зрения.

Эшер и математика

Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей. Всемирная известность пришла к Морису Эшеру в 1951 году сразу после публикации в трёх популярных журналах «The Studio», «Time» и «Life». В 1954 году в Амстердаме состоялась большая выставка Эшера, приуроченная и Международному математическому конгрессу. Каждая работа Эшера это загадка. Можно часами рассматривать его графику, ища искажения реальности, так ловко помещаемые им в архитектуру, мазанку, пейзажи сферы и другие объекты. Даже его пейзажи - это головоломки с интересным решением. От его работ невозможно устать, ведь вам предстоит постоянно открывать для себя новые, не замеченные ранее, штрихи. Графика Эшера поражает тем, что в ней нет ничего невозможного. Его работы вовлекают зрителя в противопоставление иллюзии и реальности. Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это было интересно тем, что сам Эшер не имел специального математического образования. В процессе своей работы он черпал идеи из математических статей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии. Он был очарован всевозможными парадоксами и в том числе «невозможными фигурами». Наиболее интересными для изучения идеями Эшера является всевозможные разбиения плоскости и логика трехмерного пространства.

В искусстве Мориса Эшера меня, прежде всего, привлекли паркеты. Паркетом (мозаикой) называют заполнение плоскости одинаковыми фигурами (элементами паркета), которые не перекрывают друг друга и не оставляют на плоскости пустого пространства (иногда паркетом называют заполнение плоскости несколькими фигурами, например, правильными многоугольниками). Паркеты это плоский вид орнамента. Орнаменты изучают и археологи, и этнографы, и дизайнеры, и строители…И он интересен математикам. Орнамент один из самых упорядоченных и систематических видов искусств. В нем проявляется математическая строгость организации формы, простая или усложненная система поворотов и повторов. Узор орнамента, как правило, строится по законам симметрии. Можно удивительно просто превратить случайный рисунок или фрагмент в красивый и стройный орнамент. Нужно лишь многократно повторить имеющееся изображение, соблюдая законы симметрии.

Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник.

Эшер показывает 6 возможных способов разбиения плоскости: параллелограммы, прямоугольники, квадраты, треугольники, ромбы (с углом 60 градусов), шестиугольники (с углом 120).

Посмотрите на наброски рисунков Эшера. Они наглядно демонстрируют, как художник «разбивает» плоскость на параллелограммы.

Записи, сделанные рукой художника, показывают, что он пользуется параллельным переносом и подобием. Например, в его картинах «Птицы» и «Всадники» он использует именно параллельный перенос.

В картинах «Ящерицы» и «Летающие рыбы» мы отчетливо видим поворот на 180°, т.е. центральную симметрию и поворот на 120°.

На следующей картине Эшер уже использует одновременно и перемещение и поворот. И еще гомотетию.

В ходе своей исследовательской работы, мне удалось найти довольно интересное математическое построение паркета - орнамента.

Рассмотрим на плоскости фигуру Ф — квадрат с заштрихованной половинкой, как на рисунке 7а, а также два перемещения плоскости:

F1= поворот вокруг вершины квадрата А на 90°, и F2= Sa симметрию относительно прямой а - продолжения стороны квадрата .

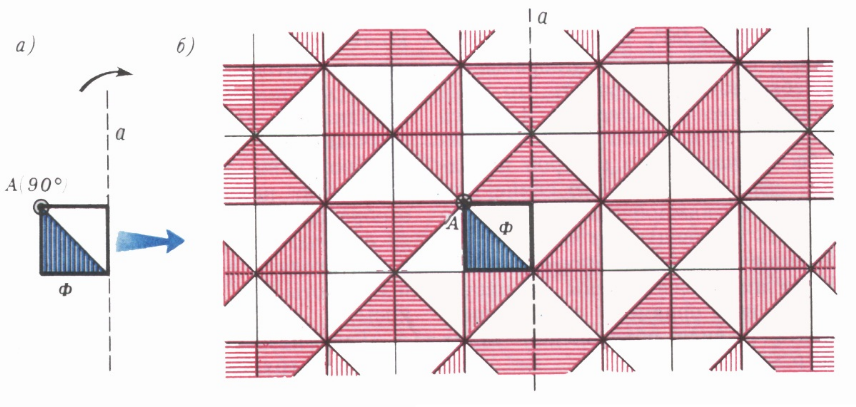
Применим к фигуре Ф всевозможные композиции перемещений F1 и F2 в произвольном порядке и в любом количестве. В результате мы получим совокупность плоских фигур, конгруэнтных Ф - так называемый плоский орнамент (с фундаментальной областью Ф и порождающими перемещениями F1и F2: он изображен на рисунке)

Более того, я встретил статью, в которой говорилось, что можно даже составить уравнение или неравенство (систему уравнений или систему неравенств) орнамента. Но пока мне самостоятельно не удалось придумать красивые уравнения для изображения орнамента.

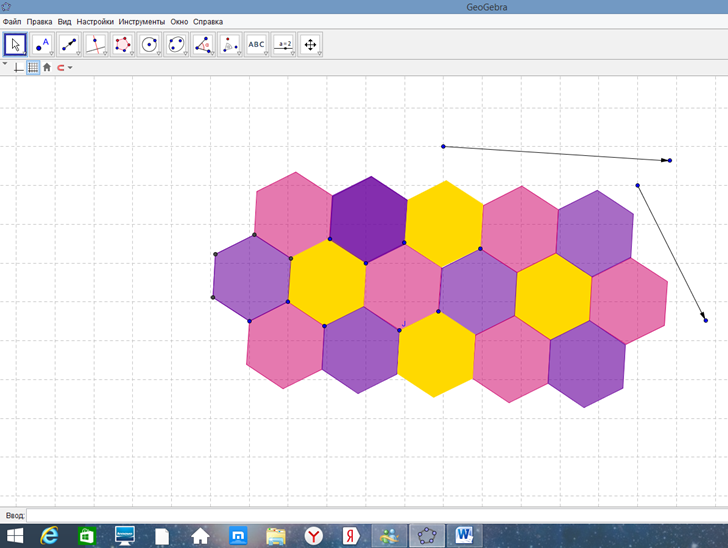
Но я создал собственный паркет, используя технику Эшера в программе «GeoGebra».

Сначала создал правильный шестиугольник.

Выбрав точку (центр поворота), повернул многоугольник на 120°.

Проделав повороты по часовой и против часовой стрелки получил часть орнамента и немного раскрасил его.

Затем воспользовался перемещением фигуры на вектор.

И перемещением же заполнил пустые ячейки орнамента.

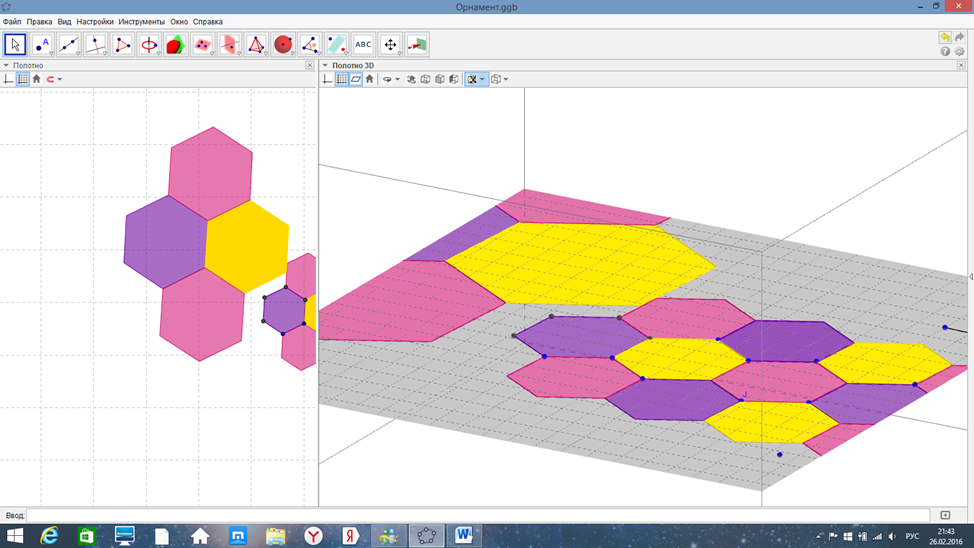
Чтобы продемонстрировать возможности программы построил несколько ячеек орнамента, воспользовавшись гомотетией с коэффициентом k=2. Так как в программе есть 3D моделирование, наложил паркет на «пол».

В журнале «Квант» за июнь 2007 года есть информация о том, как собрать одну из «невозможных фигур», которую изображал М.К.Эшер. Вот что у меня получилось:

Также с другом, который изучает информатику, мы создали небольшой виртуальный музей М.К.Эшера. Приглашаю вас окунуться в мир фантастической геометрии…

В исследования мне подсознательно хотелось опровергнуть, что красота и гармония не поддаются математическому описанию. Однако, вновь я убедился в том, что «Математика выявляет порядок, симметрию и определённость, а это – важнейшие виды прекрасного» - Аристотель. С середины прошлого века без гравюр Эшера не обходится ни одна «иллюстрированная» книга по математике, физике, топологии, не говоря уж о популярных изданиях! Советский научно-популярный журнал «Квант» публиковал Эшера свыше 20 раз, «Знание-сила» - еще больше. В оформлении учебников «Математика 10-11», автор Мордкович А. Г., использованы литографии Эшера. Его имя можно встретить и в книгах по информатике. Можно увидеть чашки, галстуки, часы и красивые ткани, украшенные паркетами Эшера.

Оказалось, что с помощью работ Эшера доступнее и интереснее можно объяснить школьникам такие математические понятия и термины, как: параллельный перенос, подобие фигур, гомотетия, равновеликие фигуры, периодичность. Эшер одним из первых стал изображать в своих картинах фракталы. Только после смерти художника учёные стали изучать свойства этих фигур и с помощью компьютеров строить то, что Эшер рисовал вручную.

Заключение:

1. В творчестве Эшера доминирует математический аспект.

2. Математики были первыми среди почитателей его таланта.

3. Прослеживается связь творчества Эшера с наукой: математикой, изобразительным искусством, физикой.

4. При работе над темой я узнали много интересного о жизни замечательного художника Эшера. Познакомился с новыми понятиями: регулярные и нерегулярные разбиения плоскости, разделом математики – топологией .

Я считаю, что цель и задачи, которые были поставлены, реализованы. Гипотеза – подтверждена. Данную работу я презентовал на внеклассном мероприятии по математике. Работа вызвала большой интерес у учащихся школы. Особенно, виртуальный музей из некоторых картин удивительного художника Мориса Корнелиса Эшера. (демонстрация «музея»)

Список использованной литературы

1. Табачников С. Текстильная геометрия. - Квант, № 7. 1990

2. Зайцева Е. Творец невозможного: художественные образы математика Мориуса Эшера.- Новое 3время, №36, 1998

3. Смирнова Е.С. Интеллектуальный театр в школе. Математика и фантазия. 56-11 класс. М. УЦ «Перспектива» 2007

4. С.Табачников Вариации на тему Эшера. – Квант. № 12, 1990

5. http://shop.escher.ru

6. http://www.worldofescher.com/

7. http://www.mcescher.com/

8. http://www.escher.ru/index.php

9. http://www2.gol.com/users/atoz/3descher/index.html

10. http://im-possible.info/russian/articles/escher_math/escher_math.html

11. http://ru.wikipedia.org/wiki/Категория:Работы_Мориса_Эшера

12. http://ru.wikipedia.org/wiki/Эшер

13. Ж. Л. Лошер, В. Ф. Вельдхуизен. Магия М. К. Эшера. — Арт-Родник, Taschen, 2007.

14. Bruno Ernst. The Magic Mirror of M. C. Escher. — Random House (New York), 1976.

15. Douglas Hofstadter. Gödel, Escher, Bach: an Eternal Golden Braid. — Basic Books, 1979. 

16. Гёдель, Эшер, Бах: эта бесконечная гирлянда. — Самара, 2001. — 752 с.

17. F. H. Bool, J. R. Kist, J. L. Locher, F. Wierda. M. C. Escher: His life and complete graphic work. — Harry N. Abrams (New York), 1982.

18. J. L. Locher. Leven en werk van M. C. Escher. — Meulenhoff (Amsterdam), 1981.

19. Doris Schattschneider. M. C. Escher: Visions of Symmetry. — Meulenhoff (Amsterdam), 2004. 

20. Wim Hazeu. M. C. Escher: Een biografie. — Harry N. Abrams (New York), 1998. 

21. M. C. Escher’s legacy: A centennial celebration / Ed. by Doris Schattschneider, Michele Emmer. — Springer (New York), 1998. , частично доступна на Google Book Search.

15