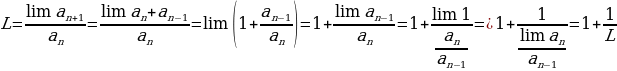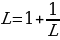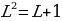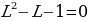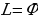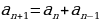МБОУ «Многопрофильная школа №17 имени маршала инженерных войск А.И.Прошлякова»
Научный проект по математике «Золотое сечение»
Выполнил ученик 11A класса:
Истомин Максим
Преподаватель:
Шатохина Ирина Федоровна
г. Рязань 2021 год
Цели проекта
Узнать, что такое золотое сечение
Найти примеры золотого сечения вокруг нас
Найти связь золотого сечения с окружающим миром
Анкетирование
В нашем классе мы провели опрос, по результатам которого выяснилось, что 83% учеников не знают о золотом сечении и его свойствах практически ничего. Нашим выступлением в классе это незнание было ликвидировано.
Определение
Наиболее емкое определение золотого сечения гласит, что меньшая часть относительно к большей, как большая ко всему целому. Приблизительная его величина – 1,6180339887. В округлённом процентом значении пропорции частей целого буду соотноситься как 62% на 38%. Это соотношение действует в формах пространства и времени.
Древние видел в золотом сечении отражение космического порядка, а Иоганн Кеплер называл его одни из сокровищ геометрии. Современная наука рассматривает золотое сечение как «ассиметричную симметрию», называя его в широком смысле универсальным правилом отражающей структуру и порядок нашего мироустройства.
Пример
Разделим отрезок на 2 части, тогда он будет разделен в крайнем и среднем отношении в терминах Евклида, иначе говоря, в «золотом» отношении, если 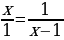
Если дроби равны, то равны и соответствующие произведения по правилу «крест-накрест»: 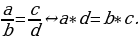 Это приводит нас к квадратному уравнению:
Это приводит нас к квадратному уравнению:
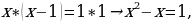
У этого уравнения есть 2 решения. Нас интересует лишь положительное:
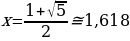
Это и есть искомое число, которое мы обозначим Ф:
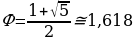
История
Преставление о золотых пропорциях имели древние египтяне, знали о них и на Руси, но впервые научное золотое сечение объяснил монах Лука Пачоли в книге «Божественная пропорция» (1509), иллюстрации, которой предположительно сделал Леонардо Да Винчи. Пачоли усматривал в золотом сечении божественное триединство: малый отрезок олицетворял Сына, большой – Отца, а целое – Святой дух.
Непосредственным образом с правилом золотого сечения связано имя итальянского математика Леонардо Фибоначчи. В результате решения одной из задач вышел на последовательность числе, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 51, 34, 55… На отношение этой последовательности к золотой пропорции обратил внимание Кеплер: «Устроена она так, что 2 младших члена этой нескончаемой пропорции дают в сумме третий член, а любые 2 последних члена, если их сложить, дают следующий член, при чем та же пропорция сохраняется до бесконечности». Сейчас ряд Фибоначчи — это арифметическая основа для расчета пропорции золотого сечения во всех его проявлениях.
Леонардо Да Винчи также много времени посвятил изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стеометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения в сторонах в золотом делении.
Со временем правило золотого сечения превратилось в академическую рутину и только философ Адольф Цейзинг в 1855 году вернул ему вторую жизнь. Он довел до абсолюта пропорции золотого сечении, сделав их универсальными для всех явлении окружающего мира. В прочем, его «математическое эстетство» вызывало много критики.
Связь золотого сечения с последовательностью Фибоначчи
История математики полна неожиданностей. Одна из них касается золотого сечения, известного еще с древних времен и тесно связанного с геометрией. Однако спустя столетия это соотношение было найдено в ряде дробей, возникших из чисто арифметической последовательности. Гением, нашедшим эту связь между геометрией и арифметикой, был один из самых выдающихся математиков средневековья Леонардо Пизанский, более известный как Фибоначчи.
Фибоначчи написал труды по геометрии, алгебре и теории чисел, но его самая знаменитая книга посвящена вычислениям. Liber Abaci («Книга абака»), опубликованная в 1202г., имеет обманчивое название (буквальное значение слова «абак» - «счетная доска»), возможно намеренно ироничное, потому что в действительности она пытается продемонстрировать преимущество арабских цифр для вычислений перед методами, основанными на применении счетов и римских цифр, которые доминировали в то время в Италии. Книга Фибоначчи положила конец этой практике, но произошло не сразу несмотря на то, что с помощью десятичных цифр было проще делать расчёты, новый метод распространялся не так быстро. Необходимо было преодолеть всякого рода сопротивление прежде всего абацистов, счетоводов, которые на протяжении веков использовали счеты. Тем не менее в конце концов алгористы, сторонники арабских цифр, победили.
Наряду с введением новых символов и методов расчета, «Книга абака» была посвящена теории чисел (например, разложению простые множители и
правилам делимости) и содержала первоклассные алгебраические задачи. Конечно, она содержала главы о ведении счетов, о распределении прибылей и убытков, а также об обмене денег. Но самый известным разделом книги является знаменитая задача о размножении кроликов, решение которой сегодня известно как последовательность Фибоначчи.
Задача формулируется следующим образом: «Сколько пар кроликов у нас
будет через год, если в январе у нас была одна пара, которая каждый месяц производит на свет другую пару, начиная с марта, пара, в свою очередь, производит свое собственное
потомство каждый месяц, начиная с марта пара, в свою очередь , производит собственное потомство каждый месяц, начиная с марта месяца, со второго месяц».
Теперь давайте посмотрим на некоторые другие связи между этими двумя понятиями. Мы воспользуемся калькулятором, чтобы найти отношения соседних чисел в последовательности Фибоначчи: 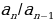 . Первые несколько результатов имеет мало общего с Ф, но мы продолжим вычисление. Что мы видим? Ответы вдруг начинают к значению Ф. В следующей таблице видно, что, начиная с десятого члена, каждый частное отличается от предыдущего меньше чем на 0,001.
. Первые несколько результатов имеет мало общего с Ф, но мы продолжим вычисление. Что мы видим? Ответы вдруг начинают к значению Ф. В следующей таблице видно, что, начиная с десятого члена, каждый частное отличается от предыдущего меньше чем на 0,001.
Таким образом, для нахождения приближённого значения Ф нет необходимости извлекать квадратные корни, достаточно просто делить друг на друга члены последовательности Фибоначчи.
Докажем это. Допустим сначала, что предел отношений членов последовательности Фибоначчи, а именно предел последовательности 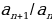 равен некоторому числу L. Запишем это следующим образом:
равен некоторому числу L. Запишем это следующим образом:
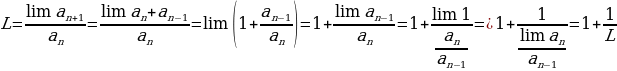
Тогда
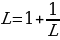
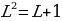
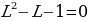
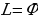
Число L описывается тем же уравнением, что и Ф, поэтому L и Ф должны иметь одинаковое значение. Таким образом, золотое сечение является пределом последовательности отношений чисел Фибоначчи. Отношений членов такой последовательности всегда будет равен Ф. Заметим, что в приведенном выше доказательстве мы использовали только это условие: 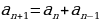

Используя цепные дроби для нахождения приближенного значения Ф, мы получим следующее выражение:
Прямоугольники и золотое сечение
В наши дни большинство людей носит в кошельках и сумочках множество карточек: кредитные карты, визитные карточки, пропуски в библиотеку и в спортзал, в также водительские права и удостоверение личности. Мы пользуемся ими ежедневно, не обращая внимания на тот факт— вовсе не случайный и немаловажный — что большинство карточек имеет одинаковый размер и форму, по крайней мере, те же пропорции.
Чтобы убедиться в этом, достаточно измерить и сравнить стороны карточек-прямоугольников. Отношение большей стороны к меньшей в большинстве случаев является числом, очень близким к 1,618, числу Ф. Поэтому не случайно, что это отношение у большинства карт является одним и тем же, это стандартные размеры.
Как и в случае подобных прямоугольников, существует простой и быстрый способ узнать, является ли прямоугольник «золотым», без измерения его сторон. Возьмём два одинаковых прямоугольника и поместим из рядом друг ща другом, один горизонтально, другой вертикально, как на следующем рисунке слева. Затем мы проведём линию через вершину А и В, как показано на рисунке справа. Если эта прямая проходит точно через вершину С, то мы имеем два «золотых» прямоугольника одинакового размера.
Свойства «золотого» прямоугольника
Если отрезать от нашего «золотого» прямоугольника квадрат, то останется прямоугольник BEFC, который также является «золотым». Проведя диагонали в двух «золотых» прямоугольниках, мы увидим, что они всегда пересекаются под прямым углом. Это справедливо как для пары AF и CE, так и для пары DE и BF (диагонали в каждой паре перпендикулярны друг к другу).
Если мы продолжим отрезать от каждого следующего «золотого» прямоугольника и каждый раз будем проводить диагонали, как на рисунке выше, мы увидим, что все получившие диагонали будут лежат на одной из пересекающихся под прямым углом диагоналей. Таким образом, они всегда буду перпендикулярны, а точка из пересечения всегда будет одной и той же точкой О
Спирали и золотое сечение
На самом удивительным образом Ф проявляется в спиралях. Предположим, у нас есть «золотой» прямоугольник, от которого мы отсекаем квадраты, получая все меньше «золотые» прямоугольники по уже знакомым нам процедуре.
Затем мы проведем четверть дуги окружности в каждом из отсекаемых квадратов. Радиус каждой из окружностей равен длине стороны прямоугольником, а центром является вершина, общая со следующим «золотым» прямоугольником. Это будут точки 1,2,3,4,5...
Таким образом мы получим линию, называемую логарифмической спиралью.
Золотое сечение в природе
Даже не вдаваясь расчёты, золото сечение может быть без труда обнаружить в природе. Так, под него попадаются отношения хвоста и тело ящерицы, расстояние между листьями на ветке, и золотое сечение, и формы яйца, если условную линию провести через её наиболее широкую часть. Белорусский учёный Эдуард Сороко, который место в пространстве, уделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм — это закручивание по спирали. Ещё Архимед, уделяя внимание спирали, вывел на основе формулы уравнения, которые сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни». С современными учёными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, средняя ДНК и даже структура галактик заключается в себе Фибоначчи.
Золотое сечение в живописи
В эпоху возрождения использования перспективы и поиск идеальных пропорции свели художников и учёных вместе. Подобно тому, как математике изучали соотношение перспективы, художники использовали проективную геометрию, чтобы изображать реалистично трёхмерные сцены. В эти наведения наряду с Рафаэлем и Дюрером ключевую роль играл Леонардо Да Винчи.
В 1435 г. появился «Тракт о живописи» Леона Баттисты Альберти, его важнейшая работа перспективе, где он изложил методы изображения реальных объектов. Идеи учёного оказались поворотными, как видно на следующих крылатых фраз: «Первое требование для художника — это знание геометрии» и «Картина является открытым окном, через который мы видим изображаемый объект».
Альберти был поглощён поиском теоретических и практических правил, определяющих работу художников, поэтому его тракты наполнены конкретными темами. Тракт «О скульптуре» он посвятил пропорциям человеческого тела, в тракте «О живописи» он сформулировал первое научное определение перспективы, а в «Десяти книгах о зодчестве» описал свою концепцию современной архитектуры, основан золотой пропорции.
Золотое сечение в архитектуре
Золотое сечение встречается в архитектуре со времен древних египтян, хотя мы не можем с уверенностью сказать, что такие пропорции использовались умышленно. Например, высота и основание Великой Пирамиды имеют непосредственное отношение к Ф.
Из всех архитектурных творений древнего мира лучше других эффект золотого сечения иллюстрируется именно Парфенон. Современное название золотого сечения, фи, происходит от имени Фидия, творца этого древнего чуда.
Конечно, крайнее и среднее отношение часто использовалось в греческой культуре, но точные измерения выявили на удивление много неточностей, вызвавших подозрение многих экспертов. Может быть людям лишь хотелось увидеть золотое сечение в пропорциях Парфенона, в то время как его строители использовали другие соотношения? Мы всегда можем насчитать 666 шагов по лестнице.
Италия эпохи Возрождения была не единственным местом, где золотое сечение использовалось при строительстве зданий. Университет Саламанки – перовое учебное заведение в Европе, известное под название «университет» - является самым старым университетом в Испании (основан в 1218г.). Его фасад был перестроен в XV веке в стиле платереско, который был характерен для эпохи исанского Возрождения и является смещением мавританского стиля и фломанской готики. Золотое сечение лижет в основе пропорций этого здания.
Вывод
Золотое число, трансцендентное сечение, божественное число... Число, не даром имеющее такое большое количество имён и очаровавшее большее блестящих умов всех времен, чем π и е вместе взятые, открыло нам и продолжает открывать много удивительных свойств. Область его применения очень велика и продолжает расширяться.
Продуктом нашего проекта стало значение многих интересных свойств золотого сечения и умение применять их в анализе различных объектов.
Источник
• В своём исследовании мы отправились на материалы книги «Золотое сечение» испанского математика и профессора Фернандо Корбалана, а также книги «Эстетика пропорций в природе и искусстве» М.Гика.
Также были использованы материалы следующих сайтов:
• http://russian7.ru/post/zolotoe-sechenie-kak-ehto-rabolael/
• https://ru.wikipedia.org/wiki/Золотое_сечение
• http:/mathematica.deagostini.ru/
• http://n-t.ru/tp/iz/zs.htm
В результате проекта нами были выполнены следующие, поставленные в начале работы задачи:
•Узнать о золотом сечении из книг и статей
• Попытаться самостоятельно привести доказательства некоторых математических свойств золотого сечения
•Рассказать о золотом сечении своим одноклассникам
• Научиться анализировать различные объекты и из свойства, например, геометрические фигуры, некоторые произведения искусства







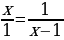
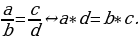 Это приводит нас к квадратному уравнению:
Это приводит нас к квадратному уравнению: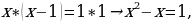
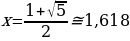
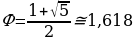
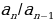 . Первые несколько результатов имеет мало общего с Ф, но мы продолжим вычисление. Что мы видим? Ответы вдруг начинают к значению Ф. В следующей таблице видно, что, начиная с десятого члена, каждый частное отличается от предыдущего меньше чем на 0,001.
. Первые несколько результатов имеет мало общего с Ф, но мы продолжим вычисление. Что мы видим? Ответы вдруг начинают к значению Ф. В следующей таблице видно, что, начиная с десятого члена, каждый частное отличается от предыдущего меньше чем на 0,001. 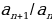 равен некоторому числу L. Запишем это следующим образом:
равен некоторому числу L. Запишем это следующим образом: