Занятие 2
Тема урока: История текстовых задач
Цели урока:
Образовательная: систематизировать, обобщить и углубить знания учащихся о текстовых задачах.
Воспитательная: формировать математическую грамотность и внимание учащихся.
Организационный момент (0.5 мин)
Актуализация знаний (5 мин)
Изложение материала (10 мин)
Домашняя работа (0.5 мин)
Подведение итогов урока (5 мин)
Рассмотрим ход урока.
Организационный момент
Деятельность учителя. Приветствует, проверяет готовность учащихся к уроку, организует внимание.
Деятельность учащихся. При заходе учителя выполняют приветствие, на столах приготовлены письменные принадлежности. Присаживаются.
Актуализация знаний.
Деятельность учителя. Просит учащихся ответить на вопрос, что такое текстовые задачи с параметром?
Деятельность учащихся. Учащиеся отвечают.
Изложение материала
Деятельность учителя. Учитель рассказывает следующую лекцию:
«Ещё в 1910 году в книге К.Ф. Лебединцева «Курс алгебры» рассматривались две характерные задачи.
Из двух станций железной дороги, расстояние между которыми 600 вёрст, вышли одновременно навстречу друг другу два поезда; первый проходит в каждый час 48 вёрст, а второй — 32 версты; через сколько часов они встретятся?
Из двух станций железной дороги, расстояние между которыми 648 вёрст, вышли одновременно навстречу друг другу два поезда; первый движется равномерно со скоростью 30 вёрст в час, а второй со скоростью 42 версты в час. Через сколько часов они встретятся?
Проводя сравнительный анализ решений данных задач, автор указывает на то, что «у них данные числа различны и ответы различны, но способы решения одинаковы» (с. 1–2).
Далее учащиеся подводятся к выведению общей формулы: «… этого мы достигнем, если условимся каждую входящую букву обозначать не словами русского языка, а латинской азбуки». После этого вводятся обозначения: расстояния между станциями — буква d, скорости первого поезда в час — а, второго — b. В заключение автор добавляет: «Тогда наша общая формула, выражающая способ решения всех подобных задач, примет следующий вид: х = 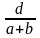 ».
».
По мнению К.Ф. Лебединцева, для составления «общих формул» «нужно только помнить, что каждая такая буква в условии есть просто сокращённое обозначение вместо таких, например, выражений: некоторое число аршин сукна, полученная при продаже прибыль и т. д.». Приведём пример класса задач, для «решения которых полезно ставить общие формулы»:
Найти площадь прямоугольника, длина которого а единиц (аршин, вёрст, метров), а ширина b таких же единиц. Ответ: х = а · b.
Автор пишет, что «эта общая формула даёт возможность находить площадь листа бумаги, куска обоев, каменной плиты, стола, стены и т. д. и может применяться в огромном числе случаев». В этой же книге обращает на себя внимание следующая задача:
Один лавочник выручает ежемесячно т руб. чистой прибыли, а другой n рублей. В настоящее время капитал первого составляет b рублей, второго а рублей. Через сколько месяцев у них будет поровну денег?
Там же приводится решение этой задачи в виде общей формулы. Затем К.Ф. Лебединцев замечает, что «если теперь придавать количествам а, b, т, n различные числовые величины, то значение и смысл ответов будут меняться, и мы поставим себе целью исследовать, какие при этом могут быть различные случаи, и каков их смысл». В качестве иллюстрации этих слов автор решает задачу в целочисленном виде и затем проводит ее исследование в общем виде (табл. 2.2).
Таблица 2.2 – Исследование задачи
| Условия относительно известных величин | Значение неизвестного | Смысл ответа |
| 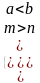 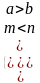 |
X 0 | Искомый момент наступит после настоящего времени. |
| 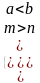 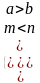 |
X | Искомый момент уже имел место до настоящего времени |
| 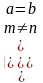 |
X = 0 | Искомый момент имеет место в настоящее время |
| 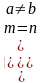 |
X = ∞ | Искомый момент не имеет места в новое время |
| 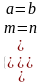 |
X = 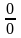 | Искомый момент имеет место во всякое время |
Таковы первые попытки выстроить методику обучения текстовым задачам с параметрами (правда, тогда они ещё так не назывались). В соответствии с описанными результатами К.Ф. Лебединцева задачи из данного класса можно разделить на две группы.
Первая группа состоит из задач, для решения которых используются общие формулы. В этом случае исследование заключается, как правило, только в выяснении ответа на единственный вопрос: при каких значениях параметров данное выражение имеет смысл, и сводится к составлению ограничений, связанных с выражением, стоящим в знаменателе дроби.
Вторая группа имеет в себе признаки первой, а именно, в процессе решения получается ответ в виде общей формулы. Однако здесь необходимо не только найти те значения параметра или параметров, при которых задача не имеет решения, но и провести полное исследование (рассмотреть все возможные случаи).
Очевидно, что такое деление (возможно, условное) является целесообразным с точки зрения дифференциации задач данного класса по уровню сложности.
Ярким представителем второй группы является «задача о курьерах», появившаяся в книге П. Никульцева, выдержавшей множество изданий:
Два курьера едут по направлению АВ. Один из них проехал через место А на h часов раньше, чем другой – через место В. Определить место и время встречи, зная, что первый курьер проезжает в час v1, а второй v2 вёрст, и что расстояние АВ равно d вёрст.
Получив формулы для расстояния до места встречи (пункта С) и для времени встречи, автор рассматривает 9 (!) случаев возможных решений задачи.
Приведенные примеры свидетельствуют о том, что ещё на рубеже XIX–XX веков в связи с бурным развитием практических приложений математики возникла потребность в составлении текстовых задач с параметрами и в разработке методики их решения. Совершенно очевидно, что включение таких задач в школьный учебный процесс способствовало развитию у учащихся математического мышления и вырабатывало у них навык абстрагирования.
В дальнейшем выходило в свет множество книг, в том или ином виде содержащих задачи с параметрами. Среди них первой отметим книгу «Упражнения по элементарной алгебре» П. Обера и Г. Папелье [3], вышедшую в нашей стране в 1941 году в переводе с французского Е.С. Березанской и А.О. Зинголь. В этой книге задачи с параметрами подаются неявно и как отдельные элементы, не образуя при этом систему.
В 1960 году в издательстве «ФИЗМАТГИЗ» вышла книга Д.К. Фаддеева и И.С. Соминского «Алгебра для самообразования», где в двух параграфах («Уравнения с буквенными коэффициентами» и «Решение систем уравнений первой степени с двумя неизвестными с буквенными коэффициентами»), опять неявно, рассматриваются задачи с параметрами. В первом случае это текстовая задача на движение с исследованием, во втором — это решение систем
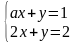 ;
; 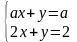 ;
; 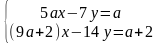
Не можем обойти и нестандартную формулировку такого задания (с. 497):
Подобрать а так, чтобы уравнения x2 + ax – 2a = 0, x2 – 2ax + a = 0 имели общий корень.
Далее решается обыкновенная текстовая задача, которая затем преобразуется в следующую текстовую задачу с параметрами:
Сторона квадрата АВСD равна l см. От его вершин в направлении обхода по часовой стрелке отложены равные отрезки Аа, Вb, Cc, Dd, и точки a, b, c, d соединены прямыми. Площадь квадрата abcd равна s cм2. Определить длину отрезка Аа.
Обозначив искомую длину через x, составив соответствующее уравнение
2x2 – 2lx + l2 – s = 0
и найдя общую формулу его решения, авторы выполняют исследование, фактически отвечая на вопрос о существовании решения задачи: при s ≥ l2/2 и при s l2.
Среди отечественных пособий такого плана следует вспомнить серию пособий для углубленного изучения школьной математики И.Х. Сивашинского, вышедших в 1965–68 гг., где тоже, не используя термина «задачи с параметрами», автор предлагает множество соответствующих задач.
Далее, закономерно, что задачи с параметрами подробно обсуждались в пособии по математике для поступающих в вузы Г.В. Дорофеева, М.К. Потапова, Н.Х. Розова, вышедшем в 1968 году в издательстве «Наука». А именно, в одном из его заключительных разделов (IV. «Нестандартные» задачи) этим задачам посвящен целый параграф (3), имеющий характерное название: «Задачи, где наиболее существенные трудности — логические». Примечательно, что там даётся подробное решение восьми задач с параметрами, семь из которых предлагались на вступительных экзаменах на механико-математический и одна — на физический факультеты МГУ имени М.В. Ломоносова в 1964–1966 гг.
Перед решением задач авторы характеризуют их как задачи, вообще говоря, повышенной трудности: «Очень серьёзные трудности вызывают обычно уравнения, неравенства и системы уравнений или неравенств с параметрами, в которых требуется найти такие значения этих параметров, при которых выполняются некоторые требования ... Эти задачи являются, пожалуй, наиболее трудными из предлагаемых на экзаменах задач, и именно потому, что они требуют логической культуры — того, чего не хватает большинству поступающих». Из этой цитаты видно, что авторы, в отличие от предыдущих авторов, действительно, уже явно используют термин «параметр». Это относится и к текстам решений задач. Например, решение второй из приведенных выше задач начинается со слов: «Пусть (a, b) — подходящая пара значений параметров…».
К сожалению, следует констатировать, что как все 8 решенных задач, так и 11 задач, предложенных для самостоятельного решения, — чисто математические, поэтому вряд ли их можно считать полноценными текстовыми задачами с параметрами.
Через два года, в 1970 году, в издательстве «Просвещение» выходит книга В.К. Маркова «Метод координат и задачи с параметрами», в которой отмечается, что «решение таких задач требует от абитуриентов высокой логической культуры и высокой техники исследования».
В 1972 году в том же издательстве вышла уже упоминавшаяся книга Г.А. Ястребинецкого «Уравнения и неравенства, содержащие параметры». В гл. 3 «Задачи с параметрами» автор обращает внимание читателя на то, что «необходимо чётко формулировать условия, указывающие область определения уравнения (неравенства) и множество допустимых значений параметров». Далее автор приводит 6 текстовых задач с параметрами, из них одна — на сплавы, другая — планиметрическая (связанная с вычислением углов треугольника через тригонометрические функции), ещё две — задачи на движение (в том числе и по окружности) и, наконец, одна задача — на работу (про путешествие туристов). Далее даётся 25 задач разного типа для самостоятельного решения.
Затем отметим книгу «Пятьсот четырнадцать задач с параметрами», вышедшую в 1991 году в Волгограде под редакцией С.А. Тынянкина, где подчёркивается, что «задачи с параметрами являются наиболее сложным в логическом и техническом плане разделом элементарной математики. В очень сильном смысле эти задачи есть индикатор общего владения абитуриентом техникой и логикой математики».
В 1993 году в издательстве МЦНМО вышел двухтомник В.В. Ткачука «Математика — абитуриенту». В аннотации автор откровенно называет его наиболее полным репетиторским курсом для подготовки к вступительным экзаменам любого уровня сложности. В первом томе имеются целые разделы «Текстовые задачи» и «Задачи с параметрами», претендующие на систематическое изложение. Однако совмещения этих понятий в настоящем пособии нет.
В связи с этим нельзя не отметить справочное пособие белорусских авторов В.В. Амелькина и В.Л. Рабцевича «Задачи с параметрами», вышедшее в Минске в 2002 году. Оно включает в себя 727 задач с параметрами и предназначено для углубленного изучения математики в средней школе и для подготовки к конкурсным экзаменам в вузы. Подробно разбираемые в пособии и предлагаемые для самостоятельного решения задачи с ответами подобраны, к сожалению, без прямых ссылок на первоисточники, но в соответствии с действующими программами вступительных экзаменов по математике и представляют практически все типы задач с параметрами. В основном, это задачи, которые предлагались абитуриентам МГУ, МФТИ, МИФИ, МВТУ, ЛГУ, НГУ, БГУ, КГУ и других вузов, включались в программы школьных олимпиад, обсуждались на страницах журнала «Квант». Пособие отличается систематичностью изложения. Особенно тщательно разобраны задачи, к которым в ранее изданных книгах давались неправильные решения или ответы.
При всей фундаментальности данного труда отметим ещё одно его непререкаемое достоинство, заключающееся в том, что в нём содержится раздел «настоящих» текстовых задач с параметрами, хотя этих задач там немного — всего 15: 7 — с решениями и 8 — для самостоятельного решения. Среди решённых — 2 задачи на движение, 3 задачи на растворы и 2 задачи на сплавы.
В 2000 году в книге Лупашевской В.Ю. и Пукаса Ю.О. «Олимпиадные задачи для ЕГЭ по математике» продолжается линия задач на растворы — дается задача с вступительного экзамена на механико-математический факультет МГУ 1981 г.:
В две бочки были налиты растворы соли, причём в первую бочку налито 16 кг, а во вторую – 25 кг. Оба раствора разбавили водой так, что процентное содержание соли уменьшилось в т раз в первой бочке, и в п раз во второй. О числах т и п известно только, что тп=т+п+3. Найти наименьшее количество воды, которое могло быть долито в обе бочки вместе.
В 2007 году в издательстве МЦНМО вышла книга А.И. Козко и В.Г. Чирского «Задачи с параметром и другие сложные задачи». Помимо стандартных сведений, в ней приведены оригинальные методы и приемы решения различных сложных задач с использованием внутрипредметных связей отдельных тем курсов алгебры и геометрии. Большинство разбираемых авторами задач взято, опять же, из вариантов вступительных экзаменов в МГУ, что говорит о том, что они являются яркими представителями класса задач повышенной трудности и вряд ли могут быть использованы при обучении математике в обычных средних школах.
Приведём ещё одну текстовую задачу — из книги Тынянкина С.А. и Тырымова А.А. «Подготовка к ГИА и ЕГЭ», в которой буквенное задание исходных данных подразумевает исследование, что позволяет нам рассматривать её как задачу с параметром:
Бригада специалистов по посадке деревьев должна посадить а деревьев. После того как бригада посадила b деревьев 0bа, часть специалистов ушла ловить раков в ближайшем озере, и оставшаяся часть бригады стала каждый час сажать на с деревьев меньше, чем сажала каждый час вся бригада. В результате все деревья были посажены за n часов. Определить d – количество деревьев, которое сажала каждый час бригада, работая в полном составе.
Можно отметить ещё несколько пособий последних лет, в которых задачам с параметрами уделялось определенное внимание — это пособия Шахмейстера А.Х. «Уравнения и неравенства с параметрами», Cеменова А.Л. и др. «ЕГЭ. 3000 задач с ответами по математике» (под ред. А.Л. Cеменова и И.В. Ященко), Сергеева И.Н. и Панферова В.С. «ЕГЭ. 1000 задач с ответами и решениями по математике».
Итак, ещё более века назад передовые учёные и учителя-методисты фактически ввели текстовые задачи с параметрами в школьный курс элементарной математики и делали попытки создать методику обучения решению этого класса задач. В современных условиях, когда такие задачи не только включаются в экзаменационные работы, которые предлагаются абитуриентам, стремящимся поступить в престижные вузы, но и могут стать атрибутом наиболее сложной части содержания ГИА и ЕГЭ, эта проблема приобретает особую актуальность и остроту».
Итак, мы с вами изучили историю текстовых задач с параметрами.







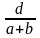 ».
». 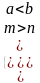
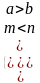
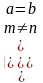
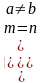
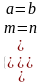
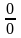
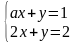 ;
; 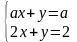 ;
;