Просмотр содержимого документа
«Итоговая контрольная работа по алгебре и началам математического анализа за курс 10 класса.»
Итоговая работа по алгебре для учащихся 10 класса (базовый и профильный уровень).
Итоговая работа проводится в конце учебного года после итогового повторения всего курса алгебры 10 класса.
На выполнение итоговой работы отводится 80 минут (2 урока).
Работа составлена в 4 вариантах, каждый вариант состоит из двух частей
Часть 1 направлена на проверку достижения уровня базовой подготовки. С помощью заданий 1 части проверяется знание и понимание важных элементов содержания (понятия, их свойства, приемы решения задач), владение основными алгоритмами.
Часть 2 состоит из заданий с развернутым ответом и направлена на дифференцированную проверку повышенного уровня владения материалом. Все задания этой части носят комплексный характер. Они позволяют проверить владение формально-оперативным алгебраическим аппаратом, способность к интеграции знаний из различных тем школьного курса, владение исследовательскими навыками, а также умение найти и применить нестандартные приемы рассуждений.
За каждое верно выполненное задание части 1 выставляется по одному баллу. Количество баллов за каждое верно выполненное задание части 2 составляет 1 – 3 балла в зависимости от правильности метода решения, формы его записи и отсутствия ошибок в вычислениях.
Критерии оценивания заданий части 2:
| № задания |
| Содержание верного ответа и указания по оцениванию (допускаются различные способы оформления решения, не искажающие его смысла) |
| Баллы |
| 11а |
| Выполнены следующие условия: | | - Уравнение решалось правильным методом - Нет ошибок в вычислениях - Ответ записан верно | | |
|
| 2 |
|
| -Уравнение решалось правильным методом - Нет ошибок в вычислениях - Ответ записан неверно |
| 1 |
|
| 0 |
| 11б |
| Выполнены следующие условия: | | - Нет ошибок в вычислениях - Верно отобраны корни уравнения - Ответ записан верно | 1 | | |
| 1 |
|
| 0 |
| 12 |
| Выполнены следующие условия: | | - Полностью соблюдается алгоритм метода интервалов - Нет вычислительных ошибок - Ответ записан верно |
| 2 |
|
| Полностью соблюдается алгоритм метода интервалов - Допущена вычислительная ошибка, в результате записан неверный ответ - Потеряно решение неравенства |
| 1 |
|
| 0 |
| 13 | Выполнены следующие условия -Правильно найдена производная -Верно вычислены критические точки -Нет вычислительных ошибок -Верно записан ответ
| 2 |
| -Правильно найдена производная | - Допущена ошибка при вычислении критических точек или вычислительная ошибка или иная другая в результате - неверный ответ | | |
|
|
| 1 |
|
| 0 |
Общее количество баллов за Часть 1 - 10 баллов;
Общее количество баллов за Часть 2 - 7 баллов;
Всего - 17 баллов.
Успешность выполнения работы определяется в соответствии с нижеприведенной шкалой:
удовлетворительно – 7 - 10 баллов;
хорошо – 11-15 баллов;
отлично – 16-17 баллов.
Спецификация итоговой работы.
Проверяемое содержание:
1 .Чтение графика
2 .Нахождение области определения функции
3 .Простейшее тригонометрическое уравнение
4 .Вычисление производной функции
5 .Упрощение тригонометрического выражения
6 .Нахождение области значений тригонометрической функции
7 .Геометрический смысл производной
8 .Связь между тригонометрическими функциями одного аргумента
9 .Нахождение промежутков монотонности функции с помощью производной
10. Нахождение точек экстремума функции с помощью производной
11а. Тригонометрическое уравнение
11б .Отбор корней тригонометрического уравнения
12 .Метод интервалов
13 .Наибольшее и наименьшее значение функции на отрезке
Текст итоговой работы.
| В а р и а н т 1 . | В а р и а н т 2 . |
| Часть 1 1. Посев семян тыквы рекомендуется проводить в мае при дневной температуре воздуха не менее +12° С. На рисунке показан прогноз дневной температуры воздуха в первой и второй декадах мая. Определите, в течение скольких дней за этот период можно производить посев тыквы. 2. Найдите область определения функции f(x)= 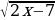 3. Решите уравнение 2sinx-1=0. 4. Найдите значение производной функции f(x)=3sinx-5cosx+7 в точке 0. 5. Упростите выражение sin2x-2sinxcosx+5tgxctgx+cos2x. 6. Найдите область значений функции f(x)=3cosx+2. 7. Вычислите угловой коэффициент касательной, проведённой к графику функции f(x)= 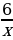 -9х в точке с абсциссой 2. -9х в точке с абсциссой 2. | 8. Известно, что sinx=0,6; xϵ(π/2; π). Найдите tgx. 9. Найдите промежутки убывания функции f(x)= 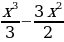 +2х +2х 10. Найдите точки экстремума функции f(x)=х4 - 16х3. Часть 2. 11. а) Решите уравнение 2cos2x+sinx+1=0; б) Укажите те из корней, которые принадлежат промежутку [π; 3,75π]. 12. Решите неравенство 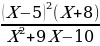 ≥0. ≥0. 13. Найдите наименьшее значение функции f(x)= 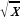 (x-6) на отрезке [1; 4]. (x-6) на отрезке [1; 4]. | 8. Известно, что cosx= - 0,8; x(π; 3π/2). Найдите ctgx. 9. Найдите промежутки убывания функции f(x)= . х х х 12 2 7 3 2 3 10. Найдите точки экстремума функции f(x)= х4 - 20х3. Часть 2. 11. а) Решите уравнение cos2x+3sinx=3; б) Укажите те из корней, которые принадлежат промежутку [-π; 3,5π]. 12. Решите нерав |
| Часть 1. 1. Первый посев семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха не менее +6° С. На рисунке показан прогноз дневной температуры воздуха в первых трех неделях апреля. Определите, в течение скольких дней за этот период можно производить посев петрушки. 2. Найдите область определения функции f(x)= 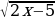 3. Решите уравнение 2cosx-1=0. 4. Найдите значение производной функции f(x)=7sinx-3cosx-8 в точке 0. 5. Упростите выражение cos2x +4tgxctgx-2sinxcosx+sin2x. 6. Найдите область значений функции f(x)=5sinx-2. 7. Вычислите угловой коэффициент касательной, проведённой к графику функции f(x)= 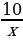 +6х в точке с абсциссой 2. +6х в точке с абсциссой 2. | 8. Известно, что cosx= - 0,8; xϵ(π; 3π/2). Найдите ctgx. 9. Найдите промежутки убывания функции f(x)= 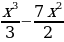 +12х +12х 10. Найдите точки экстремума функции f(x)= х4 - 20х3. Часть 2. 11. а) Решите уравнение cos2x+3sinx=3; б) Укажите те из корней, которые принадлежат промежутку [-π; 3,5π]. 12. Решите неравенство . 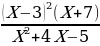 ≥0. ≥0.
13. Найдите наименьшее значение функции f(x)=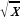 (x-15) на отрезке [4; 9]. (x-15) на отрезке [4; 9]. |
|
Ответы.
| Вариант 1 | Вариант 2 |
| Часть 1 |
| 1. 7 2. [3,5;+∞) 3. (-1)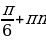 4. 3 5. 6-sin2x 6. [-1; 5] 7. -19,5 8. -0,75 9. [1; 2] 10. 12 | 1. 11 2. [2,5;+∞) 3. ±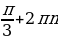 4. 7 5. 5-sin2x 6. [-7; 3] 7. 3,5 8. 0,75 9. [1; 6] 10. 15
|
| Часть 2 |
| 11а. -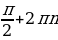 11б. 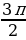 . .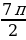 12. 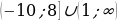 ,х=5 ,х=5 13. -4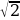 13.-22 13.-22 | 11а. 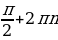 11б. 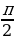 . .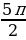 12. 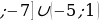 ,х=3 ,х=3 |





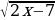
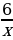 -9х в точке с абсциссой 2.
-9х в точке с абсциссой 2. 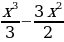 +2х
+2х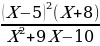 ≥0.
≥0. 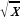 (x-6) на отрезке [1; 4].
(x-6) на отрезке [1; 4]. 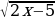
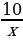 +6х в точке с абсциссой 2.
+6х в точке с абсциссой 2. 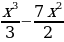 +12х
+12х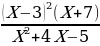 ≥0.
≥0. 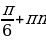
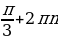
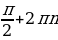
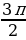 .
.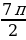
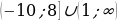 ,х=5
,х=5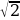 13.-22
13.-22 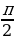 .
.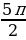

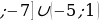 ,х=3
,х=3









