Итоговая контрольная работа по геометрии. 10 класс
Базовый уровень.
Работа проводится с целью определения уровня подготовки обучающихся 10-х классов по геометрии и выявления элементов содержания, вызывающих наибольшие затруднения. Период проведения – апрель.
Условия проведения диагностической работы:
На выполнение контрольной работы отводится 40 минут. При выполнении заданий разрешается пользоваться линейкой.
Работа состоит из двух частей.
Часть 1 направлена на проверку овладения материалом на базовом уровне. Эта часть содержит 6 заданий (с 1 по 6). Запись решения может не содержать всех обоснований, необходимо выполнить вычисления (с указанием найденных элементов), зафиксировать полученный ответ.
Часть 2 направлена на проверку владения материалом на повышенном уровне. Эта часть содержит 1 задание (№ 7) повышенного уровня сложности, требующее развернутого ответа. В этой задаче необходимо предоставить полную запись решения с обоснованием выполненных действий.
| № | Контролируемые требования к уровню подготовки | № заданий |
| 1 | Уметь определять взаимное расположение прямых в пространстве: пересекающиеся, параллельные и скрещивающиеся прямые. Уметь применять при решении задач признаки скрещивающихся прямых. Уметь определять параллельность прямых и плоскостей в пространстве: параллельные прямые в пространстве, параллельность трёх прямых, параллельность прямой и плоскости. Уметь находить углы с сонаправленными сторонами, угол между прямыми в пространстве, угол между прямой и плоскостью, двугранный угол, линейный угол двугранного угла. Уметь определять параллельность плоскостей: параллельные плоскости, свойства параллельных плоскостей. Уметь решать задачи с простейшими пространственными фигурами в пространстве: тетраэдр, параллелепипед, построение сечений. Уметь определять перпендикулярность прямой и плоскости: перпендикулярные прямые в пространстве, прямые параллельные и перпендикулярные к плоскости, признак перпендикулярности прямой и плоскости, теорема о прямой перпендикулярной плоскости. Уметь решать задачи на нахождение перпендикуляра и наклонной: расстояние от точки до плоскости, расстояние от прямой до плоскости. Уметь определять и использовать в решении задач перпендикулярность плоскостей: признак перпендикулярности двух плоскостей, теорему о трёх перпендикулярах. | 1, 2, 3, 4, 5, 6,7 |
| 2 | Умение оперировать понятиями: площадь фигуры, многогранник, правильный многогранник, сечение многогранника, куб, параллелепипед, призма, пирамида, площадь поверхности пирамиды, призмы, умение строить сечение многогранника, изображать многогранники, их сечения; умение применять свойства геометрических фигур, самостоятельно формулировать определения изучаемых фигур, выдвигать гипотезы о свойствах и признаках геометрических фигур, обосновывать или опровергать их; умение проводить классификацию фигур по различным признакам, выполнять необходимые дополнительные построения. Умение вычислять геометрические величины (длина, угол, площадь, объём, площадь поверхности), используя изученные формулы и методы, в т.ч.: площадь поверхности пирамиды, призмы. | 1,2.3,4, 5, 6, 7 |
Система оценивания отдельных заданий и работы в целом:
| Позиция в контрольной работе | Уровень сложности | Максимальный балл за выполнение задания |
| 1 | Б | 1 |
| 2 | Б | 1 |
| 3 | Б | 1 |
| 4 | Б | 1 |
| 5 | Б | 1 |
| 6 | Б | 1 |
| 7 | П | 2 |
| Всего | 8 |
Таблица соответствия отметки и количества набранных баллов:
| Отметка | Баллы |
| 5 | 7 - 8 |
| 4 | 5 - 6 |
| 3 | 3 - 4 |
| 2 | Менее 3 |
Демонстрационный вариант.
В демонстрационном варианте представлены конкретные примеры заданий, не исчерпывающие всего многообразия возможных формулировок заданий на каждой позиции варианта итоговой работы. Назначение демонстрационного варианта заключается в том, чтобы дать возможность обучающимся составить представление о структуре итоговой работы, количестве заданий, об их форме и уровне сложности.
1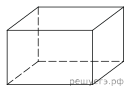 .
.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.
2.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота ‒ 10.
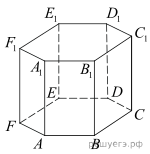
3.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 5, найдите угол между прямыми FA и D1E1. Ответ дайте в градусах.
4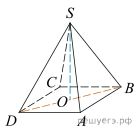 .
.
В правильной четырехугольной пирамиде SABCD точка O − центр основания, S − вершина, SO = 15, BD = 16. Найдите боковое ребро.
5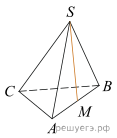 .
.
В правильной треугольной пирамиде SABC точка M − середина ребра AB, S − вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
6.
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
7. Площадь боковой поверхности правильной четырёхугольной пирамиды SABCD равна 104, а площадь полной поверхности этой пирамиды равна 120. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ её основания.
Вариант 1.
1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 12. Площадь поверхности параллелепипеда равна 192. Найдите его диагональ.
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 24, высота призмы равна 11. Найдите площадь ее поверхности
3. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 2. Найдите угол между прямыми DE и В1С1.
4. Найдите объем правильной шестиугольной призмы, все ребра которой равны 
5. Стороны основания правильной шестиугольной пирамиды равны 48, боковые ребра равны 74. Найдите площадь боковой поверхности этой пирамиды.
6. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 11. Найдите ее объем.
7. В правильной треугольной пирамиде боковое ребро равно 5, а сторона основания равна 3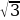 . Найдите высоту пирамиды.
. Найдите высоту пирамиды.
Вариант 2.
1. В правильной треугольной призме ABCA1B1C1 стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A1B1 и A1C1.
2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 24, высота призмы равна 11. Найдите площадь ее поверхности
3. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 2. Найдите угол между прямыми DE и В1С1.
4. В правильной четырёхугольной пирамиде РABCD точка К – центр основания, Р – вершина, РК = 48, РD = 60. Найдите длину отрезка AC .
5. В правильной треугольной пирамиде боковое ребро равно 5, а сторона основания равна 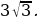 Найдите высоту пирамиды.
Найдите высоту пирамиды.
6. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и 12. Площадь поверхности параллелепипеда равна 192. Найдите его диагональ.
7. Высота правильной четырехугольной пирамиды равна 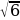 см, а боковое ребро наклонено к плоскости основания под углом 60°. Найдите площадь боковой поверхности пирамиды.
см, а боковое ребро наклонено к плоскости основания под углом 60°. Найдите площадь боковой поверхности пирамиды.
Источник заданий https://fipi.ru/ege/otkrytyy-bank-zadaniy-ege






 .
. 
 .
. 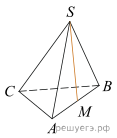 .
.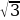 . Найдите высоту пирамиды.
. Найдите высоту пирамиды.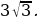 Найдите высоту пирамиды.
Найдите высоту пирамиды.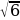 см, а боковое ребро наклонено к плоскости основания под углом 60°. Найдите площадь боковой поверхности пирамиды.
см, а боковое ребро наклонено к плоскости основания под углом 60°. Найдите площадь боковой поверхности пирамиды.









