Итоговая контрольная работа по математике за курс 11 класса (гуманитарная группа)
Структура КИМ направлена на решение двух задач: формирования у всех обучающихся базовой математической подготовки, составляющей функциональную основу общего образования.
Работа состоит из двух модулей: «Алгебра», «Геометрия».
Модуль «Алгебра» содержит 5 заданий: в части 1 – 5 заданий. Модуль «Геометрия» содержит 3 задания. Всего в работе 8 заданий.
Цель – выявление уровня освоения предметных образовательных результатов в соответствии с требованиями ООП СОО и стандарта.
На выполнение диагностической работы по математике даётся 45 минут.
Проверяемое умение и способы действия: - уметь выполнять вычисления и преобразования; - уметь решать уравнения; - уметь работать с графиками производных и первообразных, уметь вычислять производные; - моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий; -уметь применять определения, свойства, теоремы при решении задач, уметь решать практические задачи, связанные с нахождением геометрических величин; -уметь использовать при решении стереометрических задач планиметрические факты и методы.
Критерии оценивания:
Максимальный балл за работу– 8. Задания, оцениваемые 1 баллом, считаются выполненными верно, если вписан верный ответ.
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Первичные баллы | 0–3 | 4– 5 | 6–7 | 8 |
Ответы к заданиям
| № | Вариант 1 | Вариант 2 |
| 1 | -500 | 80,625 |
| 2 | -2 | 0,5 |
| 3 | 10 | 45 |
| 4 | 2 | 1500 |
| 5 | 3 | 0,96 |
| 6 | 5 | 5 |
| 7 | 10 | 7 |
| 8 | 0,5 | 0,3 |
ВАРИАНТ 1.
Часть 1.
Найдите значение выражения:

Решите уравнение 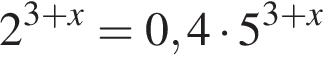 .
.
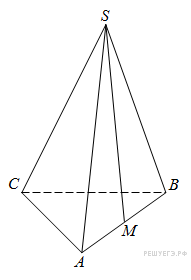
В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
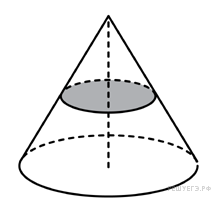
Объем конуса равен 16. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.
Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса 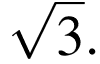
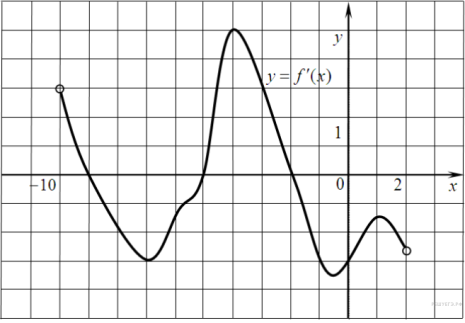
На рисунке изображен график производной функции f(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с ней.

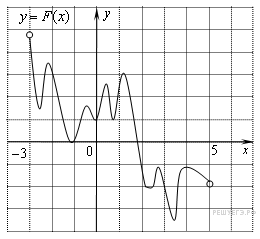
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x)=0 на отрезке [−2; 4].
На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
ВАРИАНТ 2.
Часть 1.
Найдите значение выражения:
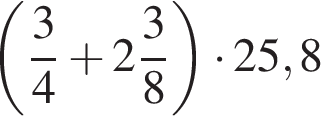
Решите уравнение 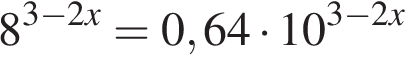 .
.
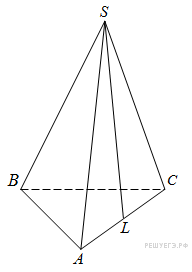
В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
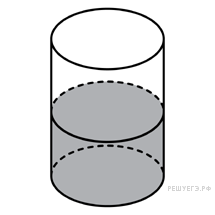
В цилиндрический сосуд налили 2000 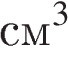 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в
воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в 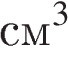 .
.
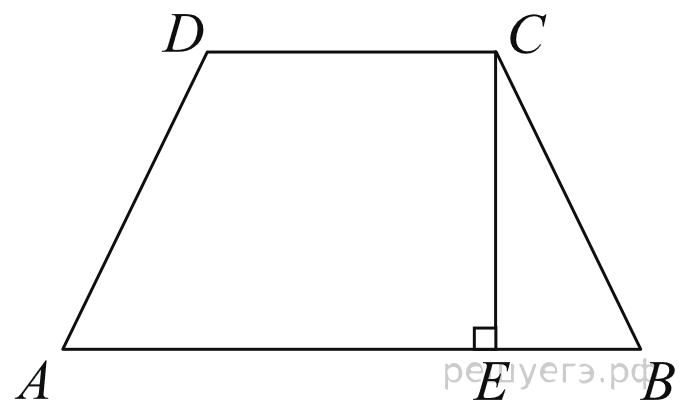
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
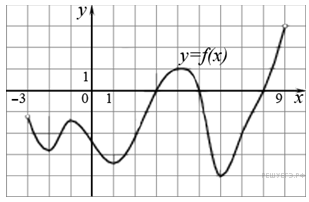
На рисунке изображен график функции y = f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 12 или совпадает с ней.
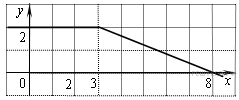
На рисунке изображён график некоторой функции  (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
(два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x).
Из множества натуральных чисел от 10 до 19 наудачу выбирают одно число. Какова вероятность того, что оно делится на 3?


























