
ВЫХОД
Математика, тренажёр
Автор – Иванов Виктор Васильевич, МБОУ «СОШ с.Вязовка» Черноярского района Астраханской области, 2020 год

Сумма чисел
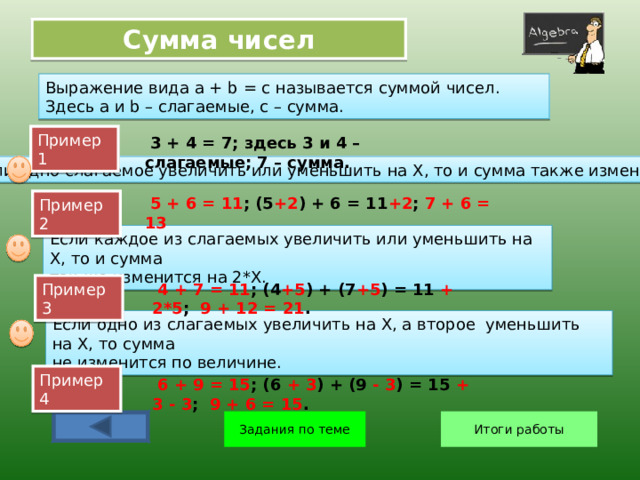
Выражение вида a + b = c называется суммой чисел. Здесь а и b – слагаемые, с – сумма.
Пример 1
3 + 4 = 7; здесь 3 и 4 – слагаемые; 7 – сумма.
Если одно слагаемое увеличить или уменьшить на Х, то и сумма также изменится.
5 + 6 = 11 ; (5 +2 ) + 6 = 11 +2 ; 7 + 6 = 13
Пример 2
Если каждое из слагаемых увеличить или уменьшить на Х, то и сумма
так же изменится на 2*Х.
Пример 3
4 + 7 = 11 ; (4 +5 ) + (7 +5 ) = 11 + 2*5 ; 9 + 12 = 21 .
Если одно из слагаемых увеличить на Х, а второе уменьшить на Х, то сумма
не изменится по величине.
Пример 4
6 + 9 = 15 ; (6 + 3 ) + (9 - 3 ) = 15 + 3 - 3 ; 9 + 6 = 15 .
Разность чисел
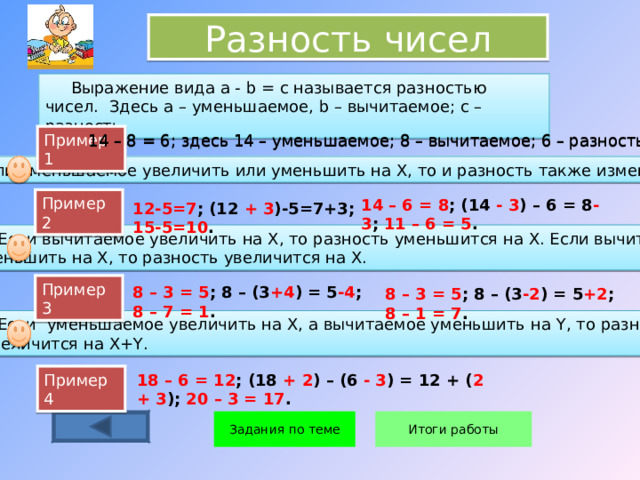
Выражение вида a - b = c называется разностью чисел. Здесь а – уменьшаемое, b – вычитаемое; с – разность.
Пример 1
14 – 8 = 6; здесь 14 – уменьшаемое; 8 – вычитаемое; 6 – разность.
14 – 8 = 6; здесь 14 – уменьшаемое; 8 – вычитаемое; 6 – разность.
Если уменьшаемое увеличить или уменьшить на Х, то и разность также изменится.
Пример 2
14 – 6 = 8 ; (14 - 3 ) – 6 = 8 -3 ; 11 – 6 = 5 .
12-5=7 ; (12 + 3 )-5=7+3; 15-5=10 .
Если вычитаемое увеличить на Х, то разность уменьшится на Х. Если вычитаемое
уменьшить на Х, то разность увеличится на Х.
Пример 3
8 – 3 = 5 ; 8 – (3 +4 ) = 5 -4 ; 8 – 7 = 1 .
8 – 3 = 5 ; 8 – (3 -2 ) = 5 +2 ; 8 – 1 = 7 .
Если уменьшаемое увеличить на Х, а вычитаемое уменьшить на Y , то разность
увеличится на X+Y .
Пример 4
18 – 6 = 12 ; (18 + 2 ) – (6 - 3 ) = 12 + ( 2 + 3 ); 20 – 3 = 17 .

Умножение чисел
Выражение вида a * b = c называется умножением чисел. Здесь а и b – сомножители, с – произведение этих сомножителей.
Пример 1
6 * 7 = 42; здесь 6 и 7 - сомножители; 42 – их произведение.
Если один из сомножителей увеличить или уменьшить в Х раз, то произведение
также изменится в Х раз.
Пример 2
5 * 4 = 20 ; (5 * 2 ) * 4 = 20 * 2 ; 10 * 4 = 40 ; 5 * ( 4 : 2 ) = 20 : 2 ; 5 * 2 = 10.
Если один из сомножителей увеличить в Х раз, а второй сомножитель увеличить
в Y раз, то произведение увеличится в X*Y раз.
Пример 3
4 * 3 = 12 ; (4 * 2 ) * (3 * 5 ) = 12 * ( 2 * 5 ); 8 * 15 = 120 .
Если один из сомножителей увеличить в Х раз, а второй уменьшить в Y раз, то
произведение изменится в X/Y раз.
3 * 4 = 12 ; (3 * 6 ) * (4 : 2 ) = 12 * (6 : 2 ); 18 * 2 = 36 .
Пример 4

Деление чисел
Выражение вида a : b = c называется делением чисел. Здесь а – делимое, b – делитель, с – частное этих чисел.
Пример 1
16 : 8 = 2; здесь 16 – делимое, 8 – делитель, 2 – частное .
Если делимое увеличить или уменьшить в Х раз, то и частное также изменится.
Пример 2
8 : 2 = 4 ; (8 *3 ): 2 = 4 *3 ; 24:2=12 .
6 : 2 = 3 ; (6 :3 ) : 2 = 3 : 3 ; 2 : 2 = 1 .
Если делитель увеличить в Х раз, то частное уменьшится в Х раз.
Пример 3
12 : 2 = 6 ; 12 : (2 * 3 ) = 6 : 3 ; 12 : 6 = 2 .
Если делимое увеличить Х раз, а делитель уменьшить в Y раз, то частное
увеличится в X*Y раз.
Пример 4
8 : 4 = 2 ; (8 * 3 ) : (4 : 2 ) = 2 * 3 * 2 ; 24 : 2 = 12 .
Итоги работы
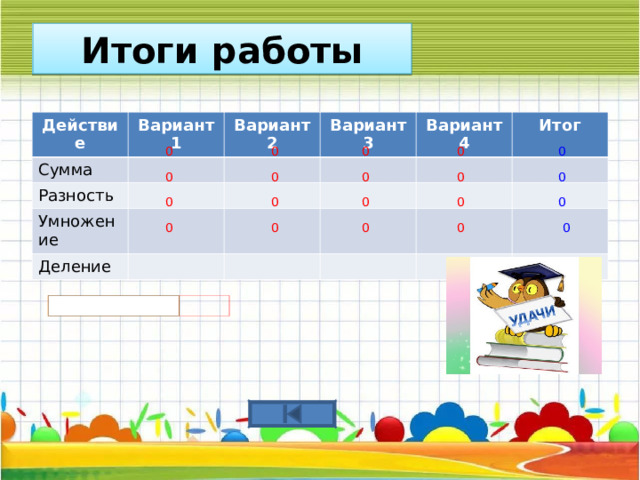
Действие
Вариант 1
Сумма
Вариант 2
Разность
Вариант 3
Умножение
Вариант 4
Деление
Итог































