Тема лекции: Амплитудная модуляция
План лекции: 1. Определение процессов модуляции и детектирования (демодуляции). 2. Временная диаграмма и математическая модель АМ-сигнала. 3. Спектр АМ -сигнала.
1. Определение процессов модуляции и детектирования (демодуляции).
Модуляция – это процесс изменения одного или нескольких параметров несущей высокочастотные колебания в соответствии с изменением параметров сигнала, воздействующего на него (модулирующего сигнала).
Параметры несущей, изменяющиеся во времени под воздействием модулирующего сигнала, называются информационными, так как в их изменениях заложена передаваемая информация. Физический процесс управления параметрами несущей и является модуляцией. Таким образом, любой модулятор1 (рис. 1) должен иметь два входа: один – для несущей, другой – для модулирующего сигнала. Модулированный (высокочастотный) сигнал на выходе модулятора зависит от времени и от модулирующего сигнала UM(t), поэтому и обозначается как функция двух аргументов UAM (UM, t).
Модулированные сигналы различаются по виду несущей и по модулируемым параметрам. В качестве несущей в настоящее время широко используются высокочастотные гармонические колебания, периодическая последовательность импульсов, реже – колебания специальной формы.
Гармоническая несущая UH(t)=UmН cos(ωt + φ), например, характеризуется тремя свободными параметрами: амплитудой, частотой и фазой. Все они могут быть информационными. Изменяя один из них при постоянстве других, получаем три основных вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ).
Модулированный сигнал при гармонической несущей в общем случае можно представить в виде:
UАМ(t)=UmAM cos ωt (1.1)
За интервал времени, в течение которого полная фаза ωt изменится на 2π, огибающая не успеет сильно измениться и ее можно считать медленно меняющейся.

Рис. 1. Модулятор
Главная особенность любой модуляции – преобразование спектра модулирующего сигнала. В общем случае происходит расширение спектра, а при гармонической несущей – перенос спектра в область около частоты несущей. Именно это обстоятельство и привело к использованию только модулированных сигналов в радиосвязи и многоканальной связи.
Модулятором называют устройство, предназначенное для получения модулированного сигнала.
2. Временная диаграмма и математическая модель АМ-сигнала.
Амплитудная модуляция – это процесс изменения амплитуды несущего высокочастотного колебания в соответствии с законом изменения мгновенных значений модулирующего низкочастотного сигнала.
Пусть модулирующий сигнал UM (см. рис. 2а) является гармоническим колебанием с частотой F, амплитудой UmM и начальной фазой, равной нулю.
В качестве несущего колебания в электросвязи обычно используют также гармонические колебания UH (см. рис. 2б) с амплитудой UMH, высокой частотой fн. На рис. 2в показана временная диаграмма АМ сигнала, полученная на основании определения АМ. На временном интервале от 0 до t, пока UM=0 (модулирующий сигнал отсутствует), отсутствует причина, вызывающая изменение амплитуды несущих колебаний, и АМ сигнал повторяет несущие колебания. В момент времени t1 появляется модулирующий сигнал,
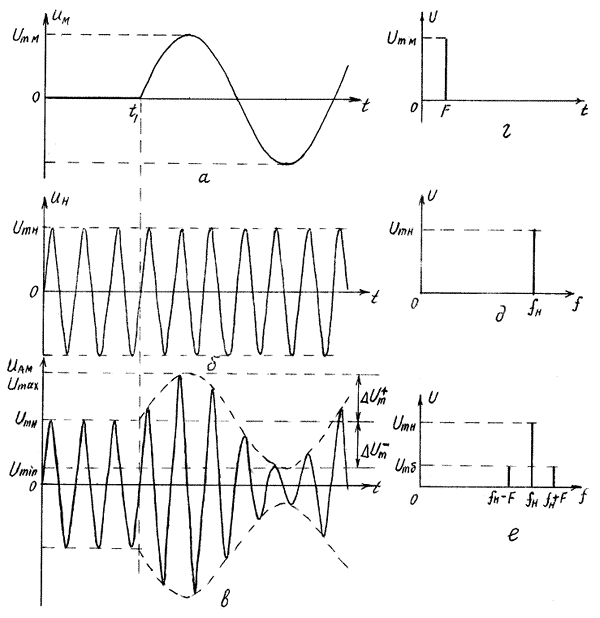
Рис. 2. Временные и спектральные диаграммы АМ-сигнала
амплитуда несущих колебаний начинает возрастать пропорционально мгновенным значениям модулирующего сигнала UM. Максимальному значению UmM модулирующего сигнала UM соответствует приращение амплитуды АМ сигнала 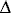 UM+ относительно UMH. Минимальному значению –UMH модулирующего сигнала UM соответствует приращение амплитуды АМ
UM+ относительно UMH. Минимальному значению –UMH модулирующего сигнала UM соответствует приращение амплитуды АМ 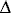 UM+ и
UM+ и  UM- должен быть равны:
UM- должен быть равны:  UM+=
UM+= UM-=
UM-= UM. Интенсивность процесса АМ (глубина модуляции) определяется коэффициентом амплитудной модуляции m. Коэффициент амплитудной модуляции равен
UM. Интенсивность процесса АМ (глубина модуляции) определяется коэффициентом амплитудной модуляции m. Коэффициент амплитудной модуляции равен 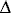 UM/ UMH
UM/ UMH
Коэффициент амплитудной модуляции может изменяться в пределах 0 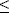 m
m 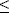 1, иногда он выражается в процентах: m%=m·100%.
1, иногда он выражается в процентах: m%=m·100%.
Если гармонические колебания с амплитудой UMH и частотой fH модулировать по амплитуде гармоническим сигналом с амплитудой UmM и частотой F, то в результате получаются гармоническое колебание UAM, которое можно рассматривать сумму следующих трех гармонических колебаний: UH с амплитудой UMH и частотой fH, с амплитудой mUMH/2 и частотой fH-F и с амплитудой mUMH/2 и частотой fH-F.
Спектр АМ сигнала
Спектр амплитуд АМ сигнала при гармоническом модулирующем сигнале представлен на рис. 2.е Согласно рис. 2.е спектр АМ сигнала является линейным (дискретным) с тремя спектральными линиями: центральная из них является спектральной линией несущего колебания с амплитудой UMH и частотой fH, а две другие – боковые с амплитудой UMб=mUMH/2. Боковые колебания с частотой fH – F называют нижней боковой, а с частотой fH + F называют верхней боковой. Амплитуды боковых колебаний одинаковы и даже при m=1 не превышают половины несущего колебания UMH
Согласно рис. 2.е ширина спектра АМ сигнала при гармоническом модулирующем сигнале равна
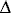 fAM=fMAX – fMIN= (fH + F) – (fH – F)=2F (1.2)
fAM=fMAX – fMIN= (fH + F) – (fH – F)=2F (1.2)
Спектр АМ сигнала при сложном модулирующем сигнале качественно определяется из следующих рассуждений. Допустим, что спектр сложного модулирующего сигнала сплошной и ограничен частотами FMIN и FMAX. Каждая частота этого спектра образует боковые составляющие с частотами fH±F. Таким образом, в спектре сложномодулированного АМ сигнала, помимо несущего колебания с частотой fH, содержатся группы верхних и нижних боковых колебаний, образующих соответственно верхнюю боковую полосу от fH + FMIN до fH + FMAX и нижнюю боковую полосу частот от fH - FMAX до fH - FMIN АМ сигнала (см. рис. 3).
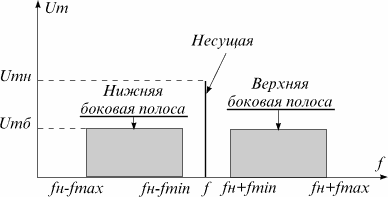
Рис 3. Спектр сложно модулированного АМ сигнала.
Согласно рис. 3 ширина спектра сложно модулированного АМ сигнала равна
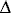 fAM=fMAX – fMIN= (fH + F) – (fH – F)=2F (1.3)
fAM=fMAX – fMIN= (fH + F) – (fH – F)=2F (1.3)
Из уравнения (1.3) следует, что ширина спектра сложно модулированного АМ сигнала 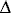 fAM равна удвоенному значению максимальной частоты fMAX спектра модулирующего низкочастотного сигнала,
fAM равна удвоенному значению максимальной частоты fMAX спектра модулирующего низкочастотного сигнала, 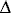 fAM=2FMAX.
fAM=2FMAX.
Энергетический анализ АМ сигнала показывает, что при 100%-ной глубине модуляции гармоническим сигналом (m=1) 66,7% мощности приходится на несущие колебания, не содержащие информации, а доля мощности обоих боковых колебаний, содержащих информацию составляет всего 33,3%. При сложном модулирующем сигнале эта доля еще уменьшается, хотя все информация в передаваемом сообщении заключается именно в боковых составляющих.
Для более эффективного использования мощности АМ сигнала используются неполночастотные АМ сигналы:
АМ сигнал, состоящий из двух боковых полос без несущей. При этом каждая боковая полоса содержит одну и ту же информацию. Ширина передаваемого спектра такая же, как и полночастотного АМ сигнала (см. рис. 4.б).
АМ сигнал, состоящий из одной боковой полосы (любой), без другой боковой полосы и без несущей. (см. рис. 4.в).

Рис. 4. Спектральные диаграммы АМ сигналов:
а - полночастотный АМ сигнал;
б - АМ сигнал из двух боковых полос без несущей;
в - АМ сигнал из одной нижней боковой полосы.
Передача одной боковой полосы обладает следующими преимуществами:
не тратится мощность на передачу несущих колебаний; за счет этого можно увеличить мощность колебаний передаваемой боковой полосы, и дальность действия связи;
при отсутствии модуляции мощность не расходуется, так как передачи несущих колебаний нет;
меньше занимаемая полоса, что позволяет отведенную для системы связи полосу частот уплотнить большим числом каналов;
требуется более узкая полоса пропускания приемника, что повышает помехозащищенность за счет снимания уровня помех в рабочей полосе частот
Вопросы для самоконтроля
1. Что такое модуляция?
2. Что называется информационными параметрами?
3. Что используется в качестве несущих колебаний?
4. Каким требованиям должны удовлетворять несущие колебания?
5. Какие основные виды модуляции вы знаете?
2. Методические указания к выполнению практической работы
«Расчет и построение спектра амплитудно-модулированного сигнала»
Цель работы: закрепить теоретический материал и выработать умения при расчете и построении спектра АМ сигнала.
Рекомендуемая литература:
Костров Б. В. Технологии физического уровня передачи данных. Учебник, -М.: Издательский центр «Академия», 2018. - 224с.
Ушаков П.А. Цепи и сигналы электросвязи. Учебник. –М.: Издательский центр «Академия», 2010. – 352с.
Пример расчета.
Задача: Рассчитать и построить спектр АМ сигнала, если 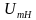 = 8B;
= 8B; 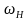 = 1π *
= 1π *  рад/с; Ω = 2π*
рад/с; Ω = 2π* рад/с; m=25%.
рад/с; m=25%.
Алгоритм расчета:
1. Определить период колебаний несущей частоты (в с, мс, мкс)
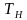 =
=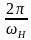 ,
, 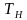 =
= 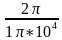 = 2*
= 2*  c = 0,2 мс
c = 0,2 мс
2. Определить значение несущей частоты (в Гц, в кГц, в МГц)
 =
= =
=  =0,5 *
=0,5 *  Гц = 5 кГц.
Гц = 5 кГц.
3. Определить период колебаний модулирующей частоты (в с, мс, мкс)
 =
=
 =
= = 1 *
= 1 *  с = 1мс.
с = 1мс.
4. Определить значение модулирующей частоты (в Гц, в кГц, в МГц)
F =  =
=  =
=  Гц = 1 КГц.
Гц = 1 КГц.
5. Определить приращение амплитуды при модуляции (В)
m =  = m
= m 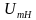 = 0,25*8=2B.
= 0,25*8=2B.
6. Определить амплитуду боковых частот.
 =
=  =
=  = 1B.
= 1B.
7. Определить значения боковых частот (в Гц, в кГц, в МГц).
.
8. Построить в масштабе спектральную диаграмму, ориентируясь на рис. 2е в лекции.
Задание
| Вариант |  , В , В
|  рад/с рад/с
| Ω, рад/с | m, % |
| 1 | 1 | 2 π* | 2π* | 10 |
| 2 | 2 | 4π* | 4 π* | 20 |
| 3 | 3 | 6π* | 6 π* | 33 |
| 4 | 4 | 8π* | 8 π* | 40 |
| 5 | 5 | 10π* | π* | 50 |
| 6 | 6 | 12π* | 1,2 π* | 67 |
| 7 | 7 | 14π* | 1,4 π* | 75 |
| 8 | 8 | 16π* | 1,6 π* | 80 |
| 9 | 9 | 18π* | 1,8 π* | 90 |
| 10 | 10 | 2π* | 2 π* | 100 |
| 11 | 1 | 30π* | 3 π* | 10 |
| 12 | 2 | 50π* | 5 π* | 20 |
| 13 | 3 | 70π* | 7 π* | 30 |
| 14 | 4 | 9π* | 9 π* | 40 |
| 15 | 5 | 11π* | 11 π* | 50 |
| 16 | 6 | 13π* | 13 π* | 60 |
| 17 | 7 | 15π* | 15 π* | 70 |
| 18 | 8 | 17π* | 17 π* | 80 |
| 19 | 9 | 19π* | 19 π* | 90 |
| 20 | 10 | 24π* | 24 π* | 100 |
| 21 | 1 | 34π* | 34 π* | 10 |
| 22 | 2 | 44π* | 44 π* | 25 |
| 23 | 3 | 54π* | 54 π* | 33 |
| 24 | 4 | 64π* | 67 π* | 40 |
| 25 | 5 | 76π* | 76 π* | 50 |
| 26 | 6 | 86π* | 86 π* | 67 |
| 27 | 7 | 94π* | 94 π* | 75 |
| 28 | 8 | 102π* | 102 π* | 80 |
| 29 | 9 | 116π* | 116 π* | 90 |
| 30 | 10 | 126π* | 126 π* | 100 |
| 31 | 1 | 134π* | 134 π* | 10 |
| 32 | 2 | 144π* | 144 π* | 20 |









 UM- должен быть равны:
UM- должен быть равны: 

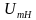 = 8B;
= 8B; 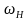 = 1π *
= 1π *  рад/с; Ω = 2π*
рад/с; Ω = 2π* рад/с; m=25%.
рад/с; m=25%.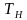 =
=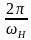 ,
, 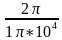 = 2*
= 2* 









