К урокам геометрии в 9 классе по теме ДВИЖЕНИЯ

ДВИЖЕНИЯ

Геометрия, 9 класс

К учебнику Л.С.Атанасяна

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

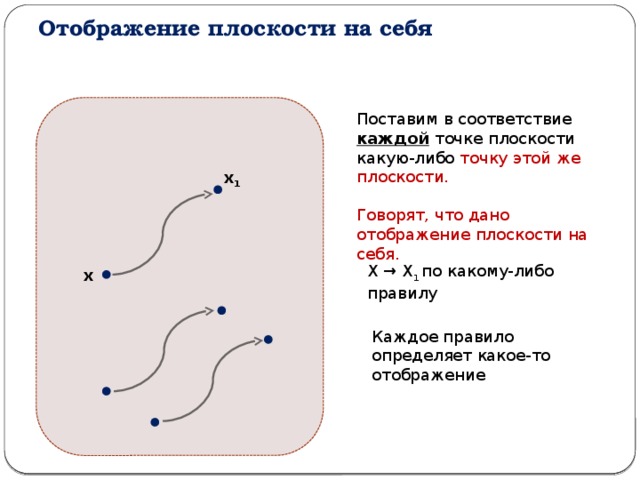
Отображение плоскости на себя

Поставим в соответствие каждой точке плоскости какую-либо точку этой же плоскости.

Говорят, что дано отображение плоскости на себя.

х 1

Х → Х 1 по какому-либо правилу

х

Каждое правило определяет какое-то отображение

Осевая симметрия

Пусть дана какая-то прямая m , которую назовем осью симметрии. Осевой симметрией называется отображение плоскости на себя, при котором каждой точке Х ставится в соответствие точка Х 1 по следующему правилу:

m

М 1

X 1

Как для точки М построить точку М 1 ?

Из точки М опустим перпендикуляр МР на прямую m.

Отложим на прямой МР отрезок РМ 1 , равный отрезку МР.

Точка, лежащая на прямой m, симметрична сама себе

X

Р

К

М

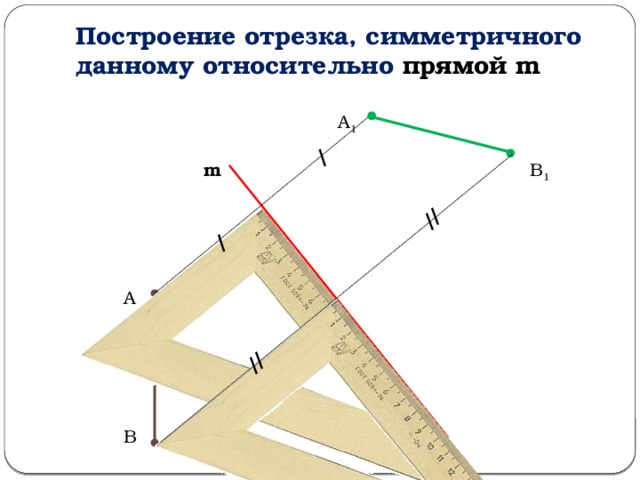
Построение отрезка, симметричного данному относительно прямой m

A 1

m

B 1

A

B

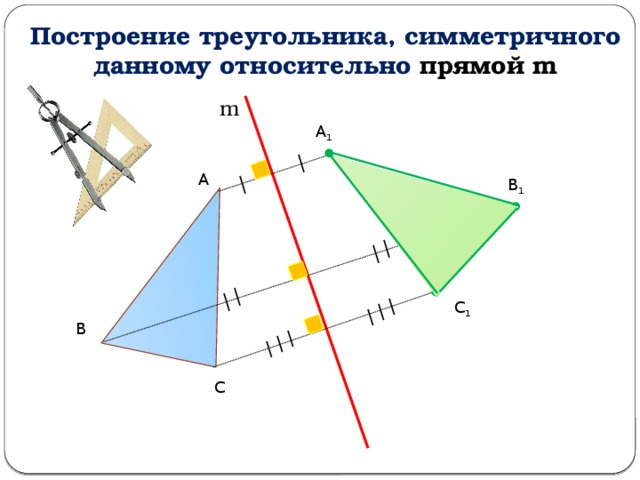
Построение треугольника, симметричного данному относительно прямой m

m

А 1

А

В 1

С 1

В

С

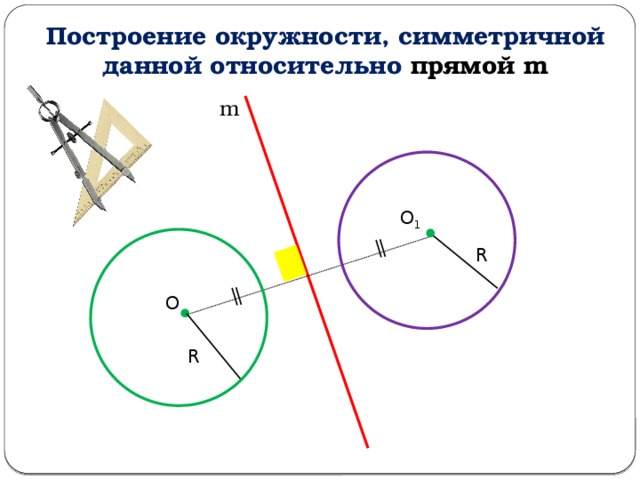
Построение окружности, симметричной данной относительно прямой m

m

О 1

R

O

R

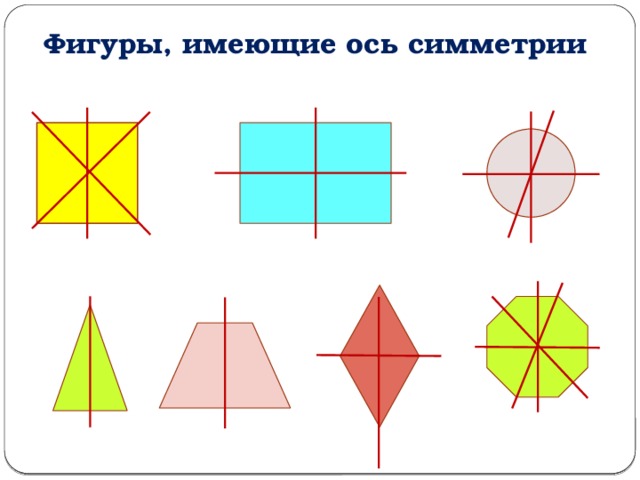
Фигуры, имеющие ось симметрии

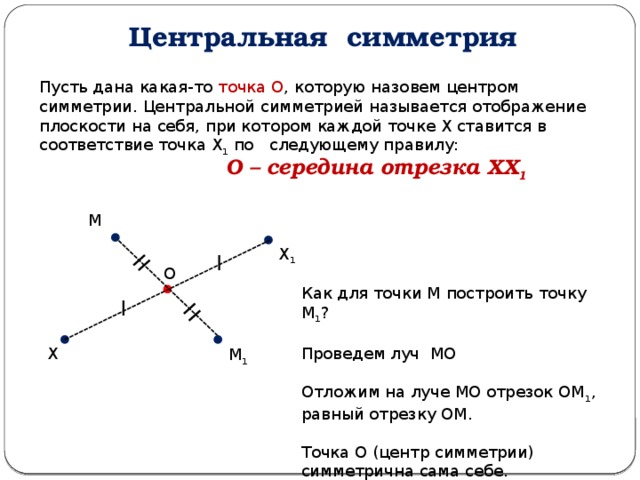
Центральная симметрия

Пусть дана какая-то точка О , которую назовем центром симметрии. Центральной симметрией называется отображение плоскости на себя, при котором каждой точке Х ставится в соответствие точка Х 1 по следующему правилу:

О – середина отрезка ХХ 1

М

Х 1

О

Как для точки М построить точку М 1 ?

Проведем луч МО

Отложим на луче МО отрезок ОМ 1 , равный отрезку ОМ.

Точка О (центр симметрии) симметрична сама себе.

Х

М 1

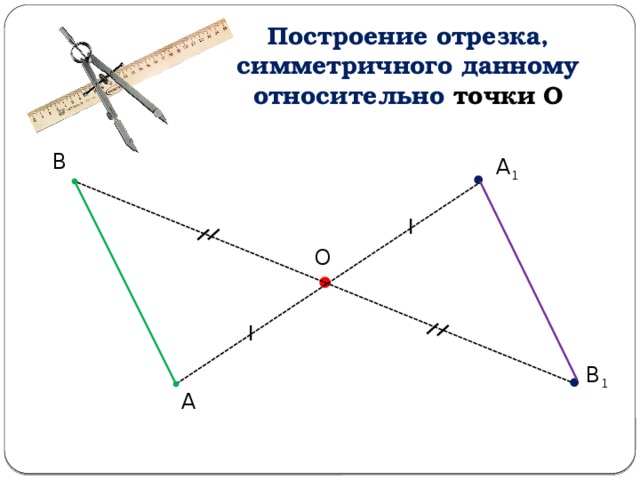
Построение отрезка, симметричного данному относительно точки О

B

A 1

О

B 1

A

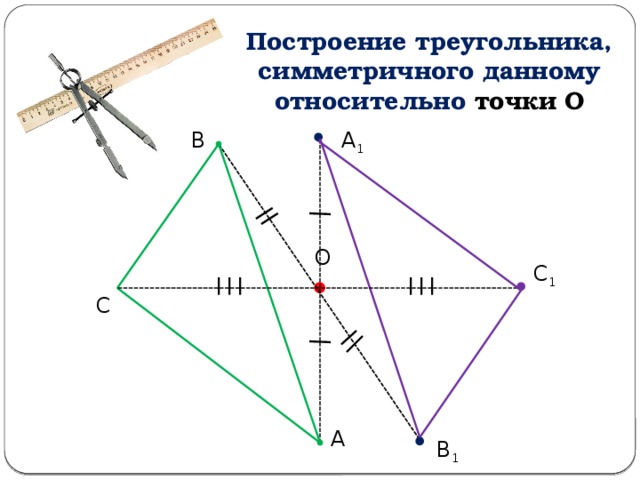
Построение треугольника, симметричного данному относительно точки О

B

A 1

О

С 1

С

A

B 1

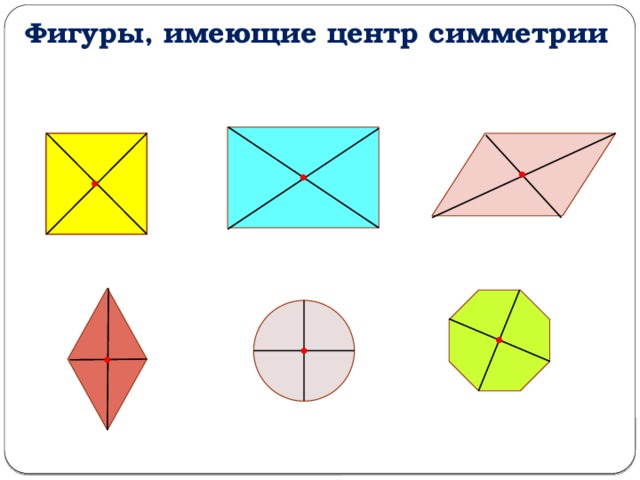
Фигуры, имеющие центр симметрии

Параллельный перенос

Х

Как для точки М построить точку М 1 ?

От точки М отложим вектор ММ 1 , равный данному вектору а

Х 1

М

М 1

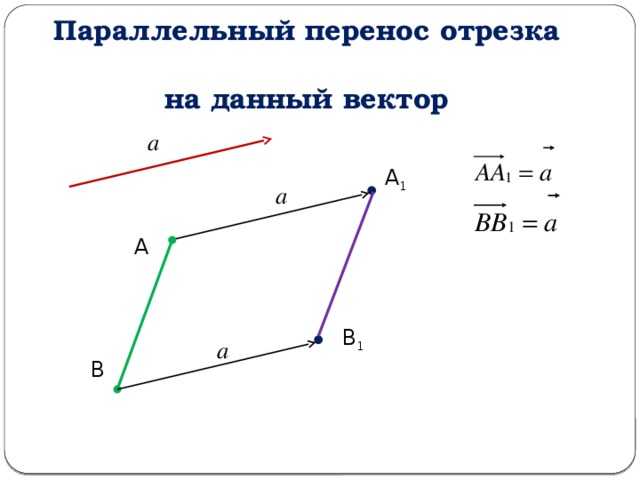
Параллельный перенос отрезка на данный вектор

А 1

А

В 1

В

С

А

В

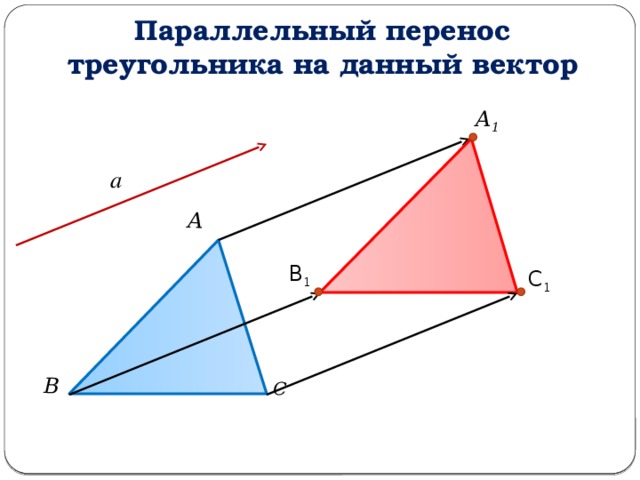
Параллельный перенос треугольника на данный вектор

А 1

В 1

С 1

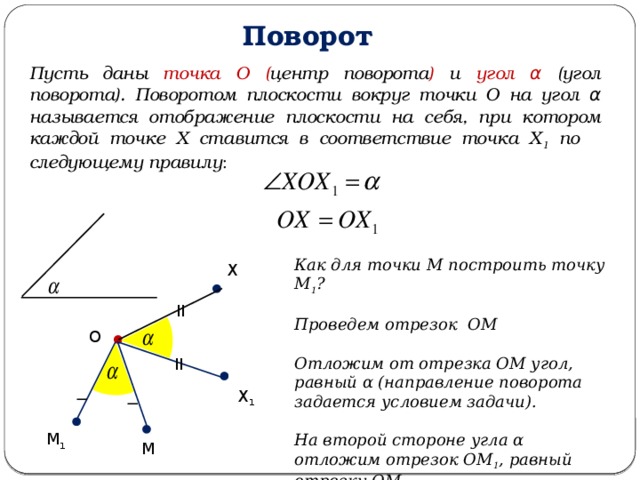
Поворот

Пусть даны точка О ( центр поворота ) и угол α (угол поворота). Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждой точке Х ставится в соответствие точка Х 1 по следующему правилу :

Как для точки М построить точку М 1 ?

Проведем отрезок ОМ

Отложим от отрезка ОМ угол, равный α (направление поворота задается условием задачи).

На второй стороне угла α отложим отрезок ОМ 1 , равный отрезку ОМ.

Х

II

О

II

Х 1

̶

̶

М 1

М

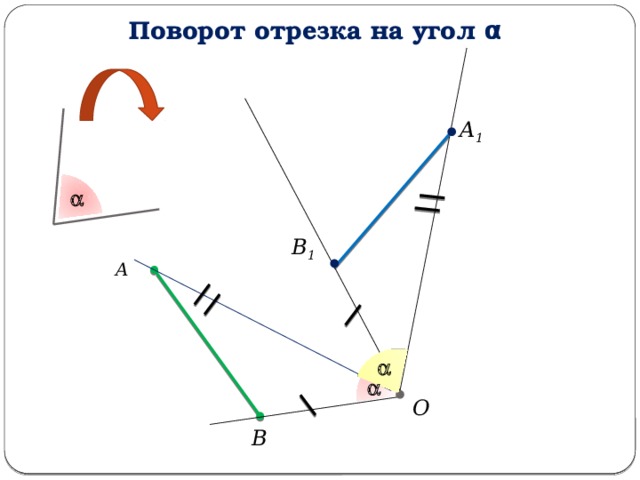
Поворот отрезка на угол α

А 1



В 1

А





О

В

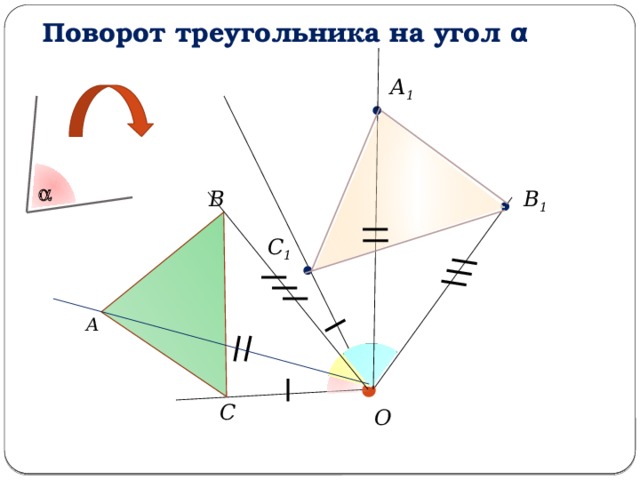
Поворот треугольника на угол α

А 1



В

В 1

С 1

А

С

О

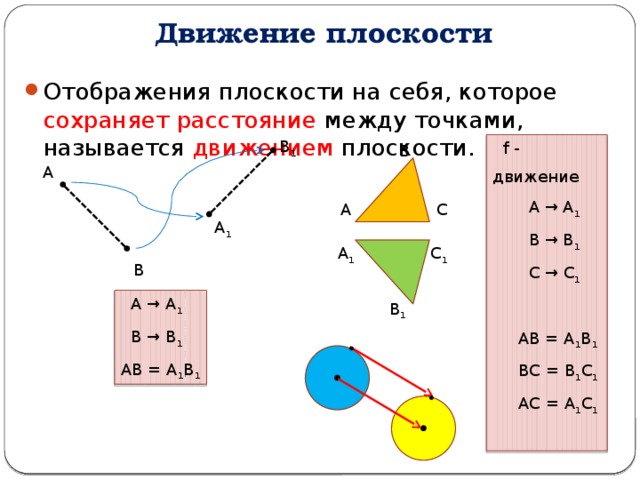
Движение плоскости

• Отображения плоскости на себя, которое сохраняет расстояние между точками, называется движением плоскости.

В 1

f - движение

А → А 1

В → В 1

С → С 1

АВ = А 1 В 1

ВС = В 1 С 1

АС = А 1 С 1

В

А

С

А

А 1

С 1

А 1

В

А → А 1

В → В 1

АВ = А 1 В 1

В 1

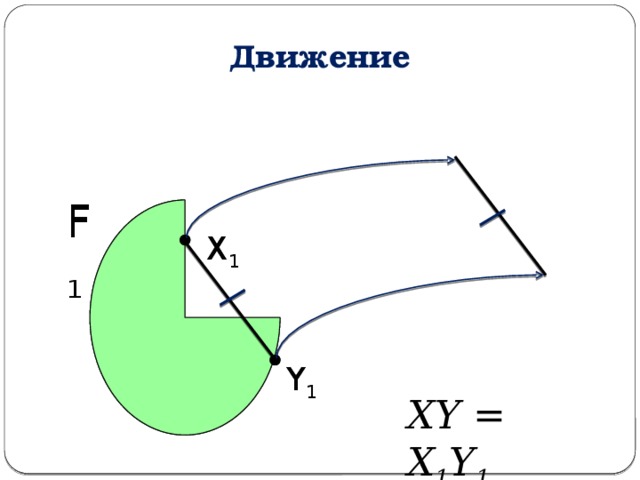
Движение

F 1

F

X 1

X

Y

Y 1

XY = X 1 Y 1

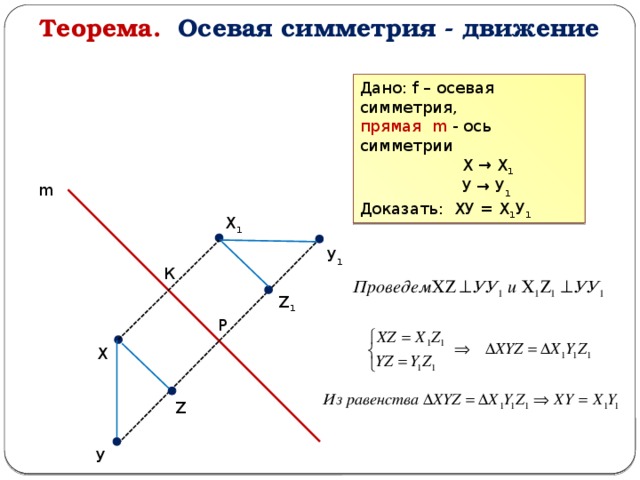
Теорема. Осевая симметрия - движение

Дано: f – осевая симметрия,

прямая m - ось симметрии

Х → Х 1

У → У 1

Доказать: ХУ = Х 1 У 1

m

X 1

У 1

К

Z 1

Р

X

Z

У

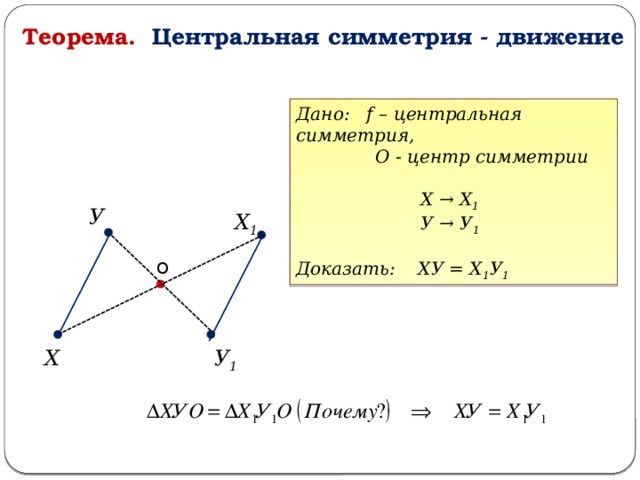
Теорема. Центральная симметрия - движение

Дано: f – центральная симметрия,

О - центр симметрии

Х → Х 1

У → У 1

Доказать: ХУ = Х 1 У 1

У

Х 1

О

У 1

Х

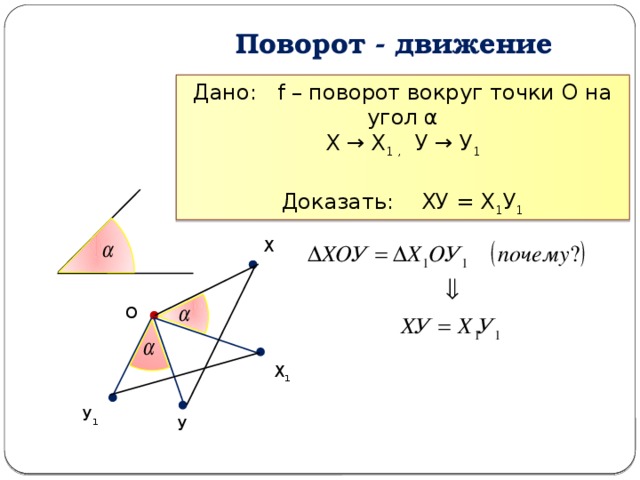
Поворот - движение

Дано: f – поворот вокруг точки О на угол α

Х → Х 1 , У → У 1

Доказать: ХУ = Х 1 У 1

Х

О

Х 1

У 1

У

Свойства движения

1 . При движении отрезок отображается на отрезок

Р

В

А

Р 1

А 1

В 1

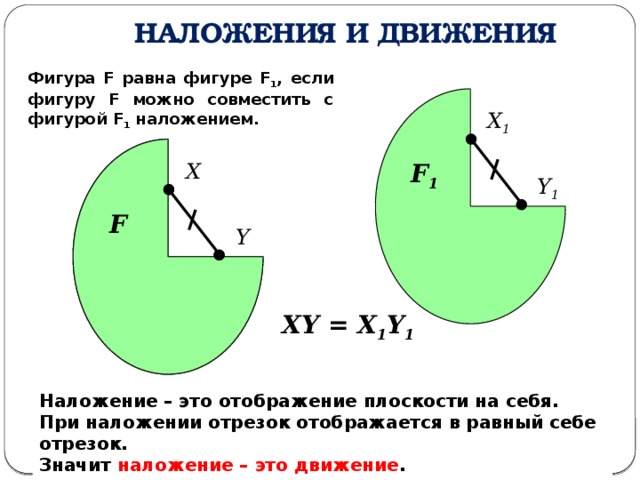
Наложения и движения

Фигура F равна фигуре F 1 , если фигуру F можно совместить с фигурой F 1 наложением.

X 1

X

F 1

Y 1

F

F

Y

XY = X 1 Y 1

Наложение – это отображение плоскости на себя.

При наложении отрезок отображается в равный себе отрезок.

Значит наложение – это движение .

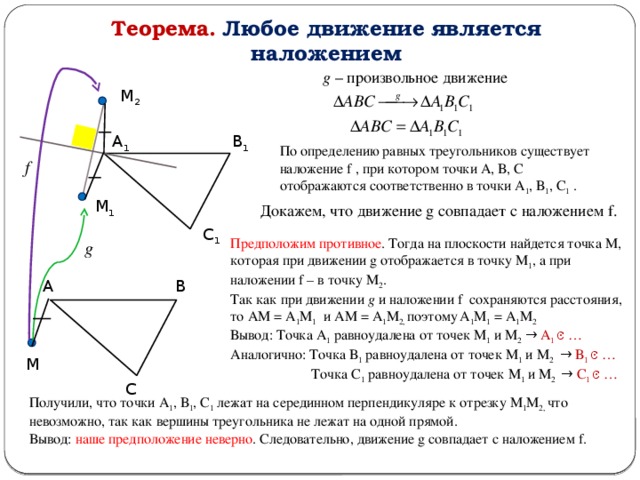
Теорема. Любое движение является наложением

g – произвольное движение

М 2

В 1

А 1

По определению равных треугольников существует наложение f , при котором точки А, В, С отображаются соответственно в точки А 1 , В 1 , С 1 .

f

М 1

Докажем, что движение g совпадает с наложением f.

С 1

Предположим противное . Тогда на плоскости найдется точка М, которая при движении g отображается в точку М 1 , а при наложении f – в точку М 2 .

Так как при движении g и наложении f сохраняются расстояния, то АМ = А 1 М 1 и АМ = А 1 М 2, поэтому А 1 М 1 = А 1 М 2

Вывод: Точка А 1 равноудалена от точек М 1 и М 2 → А 1 ͼ …

Аналогично: Точка В 1 равноудалена от точек М 1 и М 2 → В 1 ͼ …

Точка С 1 равноудалена от точек М 1 и М 2 → С 1 ͼ …

g

В

А

М

С

Получили, что точки А 1 , В 1 , С 1 лежат на серединном перпендикуляре к отрезку М 1 М 2, что невозможно, так как вершины треугольника не лежат на одной прямой.

Вывод: наше предположение неверно . Следовательно, движение g совпадает с наложением f.