Просмотр содержимого документа
«Как работать с заданиями №7 (ЕГЭ)»
Задание №7 (ЕГЭ)
Как работать если
на рисунке изображен график функции y = f(x), надо ответить на вопросы, связанные с производной,
или на рисунке изображен график первообразной y = F(x) (это график функции), надо ответить на вопросы, связанные с функцией y = f(x) (это производная y = F(x)),
или изображен график пройденного расстояния S = S(t) (это формула функции), надо ответить на вопросы, связанные со скоростью (производная пути).
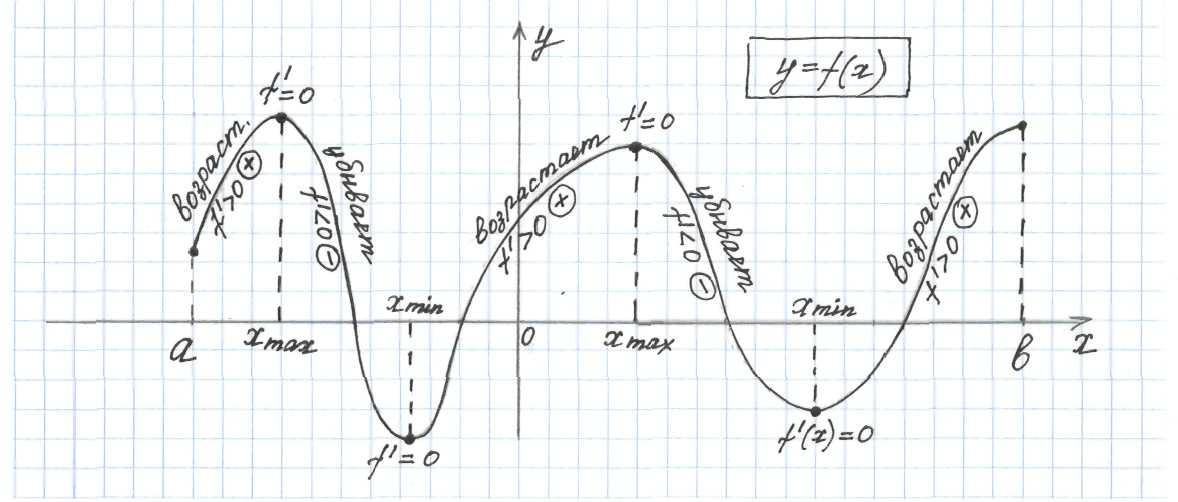
Если график задан на промежутке [a; b], то через числа a и b провести вертикальные пунктирные линии.
Жирно выделить часть графика на этом отрезке.
Обводить график слева направо.
Если поднимаемся вверх, то над графиком записать функция возрастает, под графиком f '(x) 0 (производная положительная «+»).
Если опускаемся вниз, то над графиком записать функция убывает, под графиком f '(x) (производная отрицательная « - »).
Если слева на право, функция меняет возрастание на убывание, то это точка максимума и производная в этой точке равна нулю (f '(x) = 0).
Если слева на право, функция меняет убывание на возрастание, то это точка минимума и производная в этой точке равна нулю (f '(x) = 0).
Внимание!!!
Если изображен график функции и несколько чисел на оси OX, просят найти наименьшее или наибольшее значение производной, то
Если наибольшее: выбрать числа, где производная положительная, через точки касания провести касательную и луч параллельный оси OX (вправо), где угол больше там и производная больше.
Если наименьшее: выбрать числа, где производная отрицательная, через точки касания провести касательную и луч параллельный оси OX (вправо), где угол меньше там и производная меньше.

Задание №7 (ЕГЭ)
Как дать правильный ответ, если сказано:
На рисунке изображен график производной функции f(x). Значит, изображен график y = f '(x).
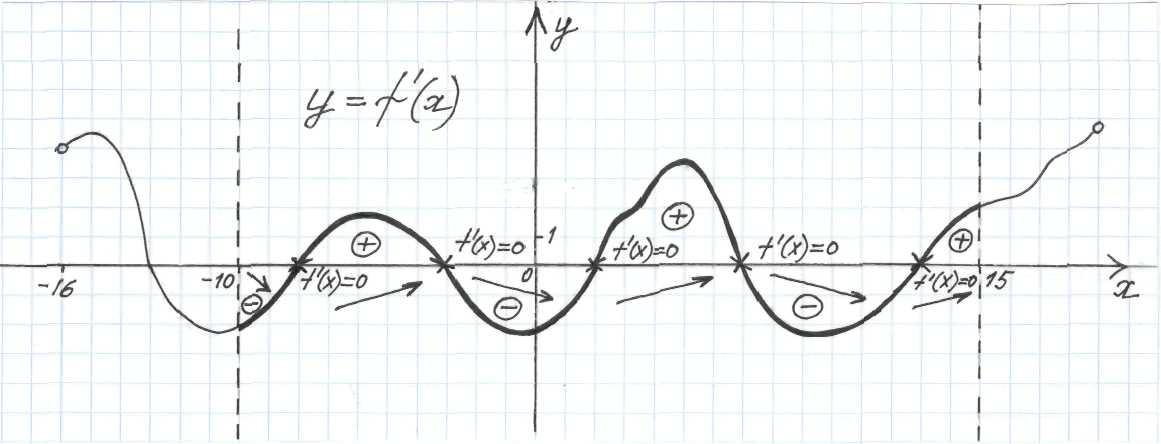
На рисунке изображен график производной функции f(x) на интервале (-16; 19). Отвечать на вопросы на отрезке [-10; 15].
Через концы заданного отрезка (найти числа на оси OX) провести вертикальные линии (это пунктирные).
Жирно выделить часть графика на этом отрезке.
Крестиком отметить точки пересечения графика с осью OX, здесь производная равна нулю. На чертеже около крестика записать f '(x) = 0.
Ось Ox (горизонтальная) делит график производной функции на части:
Если часть графика лежит выше оси Ox, здесь производная положительная (вверху поставить знак плюс «+», внизу нарисовать стрелку вверх (это значит, функция возрастает)).
Если часть графика лежит ниже оси Ox, здесь производная отрицательная (внизу поставить знак «-»), здесь внизу изобразить стрелку вниз (это значит, функция убывает).
Если двигаться по оси Ox от левого конца заданного отрезка (левый пунктирный конец) к правому концу, то:
Если при переходе через точку, где производная равна нулю (это крестик) производная меняет знак с минуса «-» на плюс «+», а функция убывание на возрастание , то эта точка (смотрят какой у этой точки x) минимума.
Если до точки (слева) стоял знак производной плюс «+», а после этой точки знак производной минус «-», при переходе через эту точку функция меняет возрастание на убывание , то эта точка (смотрим какой у этой точки x) максимума.
Если просят найти точки экстремума: это точки максимума и минимума вместе.
Если по графику производной надо выяснить, в какой точке заданного отрезка функция принимает наибольшее или наименьшее значение, то надо посмотреть на график и выделить вертикальными пунктирными линиями отрезок.
Если производная на этом отрезке отрицательная «-», а функция убывает , то наибольшее значение будет в левой точке, наименьшее в правой точке заданного отрезка.
Если производная положительная «+», а функция возрастает , то наименьшее значение в левой точке, наибольшее значение в правой точке заданного отрезка.
Если просят найти количество точек, в которых касательная параллельна прямой y = a (y =6; y =-2; и т.д.), формула без x (нет x), это значит угловой коэффициент (число перед x, его нет так как нет x) равен нулю. k = 0, но k = f '(x) = tgα. Если k = 0, то f '(x) = 0 (производная равна нулю). Тогда считаем точки, где производная равна нулю (крестики).


Если просят найти количество точек, в которых касательная параллельна заданной прямой y = kx +m (у = -2 x + 4; y = 3 x -6) тогда надо обвести кружком число, стоящее перед x вместе со знаком (угловой коэффициент), записать k = -2 или k = 3. Но k = f '(x), значит, производная равна этому числу f '(x) = -2; f '(x) = 3. Дальше на оси Oy найти это число и через него провести прямую, параллельную оси Ox. Посчитать количество точек пересечения, проведенной прямой с жирно выделенным графиком, это число записать в ответ.
Внимание!!!
Несколько раз внимательно прочитайте задание, жирно обведите вопрос, постарайтесь понять, что Вас просят найти, а дальше ищите и не забывайте записать ответ, проверив три раза!!!

Задание №7 (ЕГЭ)
I способ
Знаем!!! f '(x₀) = tgα = k
Чтобы найти f '(x₀) найдем tgα. tgα = 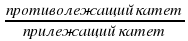
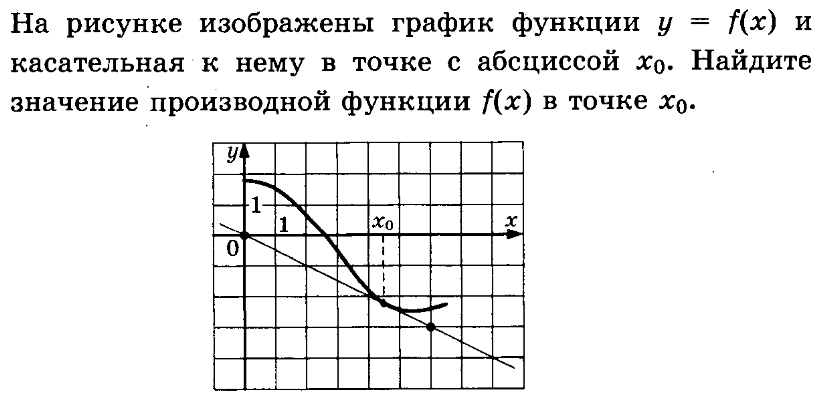
Если прямая убывающая (имеет вид ), то f '(x₀) = - tgα
На прямой найти две жирные точки. Если таких нет, то на прямой надо выделить жирно две точки, которые будут вершиной клетки (узловые точки).
Через верхнею точку, провести вертикальную (параллельную оси Oy) прямую.
Через нижнею точку горизонтальную (параллельную оси Ox) прямую.
Проведенные прямые вместе с касательной образуют прямоугольный треугольник, его нужно жирно выделить.
В прямоугольном треугольнике выделить острый угол около горизонтального катета, обозначить его буквой α.
Записать tgα = 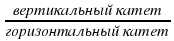 (длины катетов посчитать по клеткам).
(длины катетов посчитать по клеткам).
Полученную дробь заменить десятичной.
Записать ответ f '(x₀) = - tgα
Перенести в бланк ответов.
Задание №7 (ЕГЭ)
I способ
Знаем!!! f '(x₀) = tgα = k
Чтобы найти f '(x₀) найдем tgα. tgα = 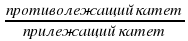
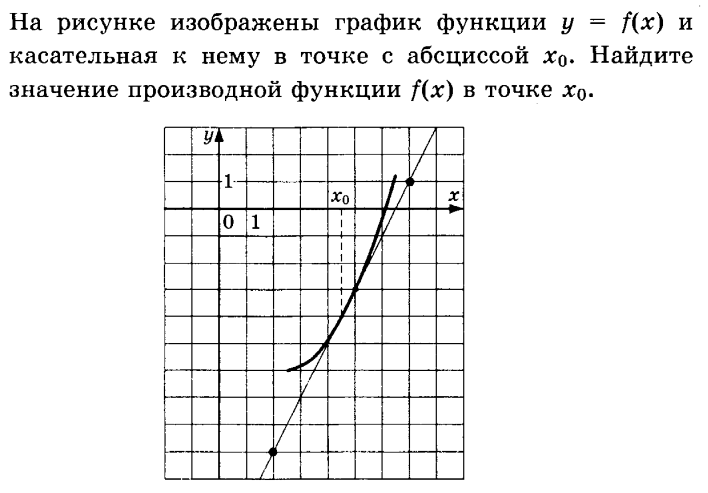
Если прямая возрастающая (имеет вид ), то f '(x₀) = tgα
На прямой найти две жирные точки. Если таких нет, то на прямой надо выделить жирно две точки, которые будут вершиной клетки (узловые точки).
Через верхнею точку, провести вертикальную (параллельную оси Oy) прямую.
Через нижнею точку горизонтальную (параллельную оси Ox) прямую.
Проведенные прямые вместе с касательной образуют прямоугольный треугольник, его нужно жирно выделить.
В прямоугольном треугольнике выделить острый угол около горизонтального катета, обозначить его буквой α.
Записать tgα = 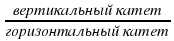 (длины катетов посчитать по клеткам).
(длины катетов посчитать по клеткам).
Полученную дробь заменить десятичной.
Записать ответ f '(x₀) = tgα (без минуса)
Перенести в бланк ответов.
Задание №7 (ЕГЭ)
II способ
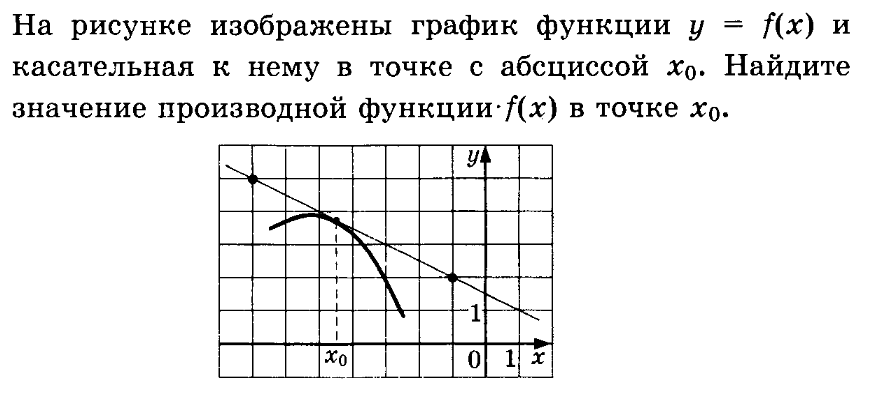
Знаем, что f '(x₀) = tgα = k , где k – угловой коэффициент касательной
Записать уравнение прямой y = k∙x + m
На касательной выбрать две точки А (-7; 5) и В (-1; 2)
В уравнение прямой подставить координаты точек
y = k∙x + m А (-7; 5) x =-7; y = 5 5 = k∙(-7) + m
y = k∙x + m В (-1; 2) x =-1; y = 2 2 = k∙(-1) + m
Составить систему
 -7∙k + m = 5, -6∙k = 3, k = -
-7∙k + m = 5, -6∙k = 3, k = - 
-1∙k + m = 2; -1∙k + m = 2;
Т.к. k = f '(x₀), то f '(x₀) = - 









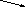

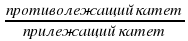

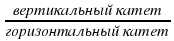 (длины катетов посчитать по клеткам).
(длины катетов посчитать по клеткам).