«Как стать «миллионером», решив «такую легкую» задачу»

Районный конкурс работ исследовательского характера (конференция) учащихся по учебным предметам

Секция «Естественно-математическая»

«Как стать «миллионером», решив «такую легкую» задачу»

Автор работы:

Лупов Кирилл Игоревич, 7 класс

ГУО «Лазовичский учебно-педагогический комплекс детский сад-средняя школа Клецкого района»

Руководитель работы:

Кирик Тамара Александровна, учитель математики, ГУО «Лазовичский учебно-педагогический комплекс детский сад-средняя школа Клецкого района»

г. Клецк, 2021 г.

Оглавление

Введение 4

Oсновная часть

Глава 1. Леонард Эйлер и его вклад в развитие топологии 6

1.1. Что такое топология

1.2. Bклад Л.Эйлера в развитие науки топологии

Глава 2. Уникурсальный граф 7

2.1. Что такое уникурсальный граф

Глава 3. Oписание работы 9

3.1. Исследование свойства уникурсального графа и полученные

результаты Заключение 15

Cписок использованных источников 16

Приложения 17

Aннотация

В своей работе я попытался показать, что изучив такое свойство графа, как уникурсальность, действительно довольно просто можно решать разнообразные математические задачи, а также можно найти применение этих знаний в повседневной жизни.

Родившись при решении головоломок и занимательных игр, теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Графы буквально вездесущи. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей. За последние четыре десятилетия теория графов превратилась в один из наиболее бурно развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений. Применяется при проектировании интегральных схем и схем управления, при исследовании автоматов, логических цепей, блок-схем программ, в экономике и статистике, химии и биологии, в теории расписаний.

Цель работы: определить и проверить свойство уникурсального графа и его использование для решения задач-головоломок.

В работе проведена связь метода решения задач о мостах с понятием уникурсальный граф. Получен вывод, что метод решения задач, предложенный Л.Эйлером, есть способ доказательства свойства графа, соответствующего задаче, быть уникурсальным.

Проверена возможность графа иметь одну вершину нечётного индекса, и получен результат: уникурсальный граф не может иметь только одну вершину нечётного индекса.

Исследованы случаи разрешимости и неразрешимости задач- головоломок (фигур, вычерчиваемых одним росчерком), получен вывод, что случаи возможности и невозможности вычерчивания одним росчерком фигур совершенно те же, что и в задаче о мостах. А решение их основывается на свойстве уникурсального графа.

Вместе с тем вопрос разрешимости или неразрешимости задачи имеет и практическое значение, в частности для того, чтобы понимать и уметь обосновывать, что не всякую предлагаемую задачу можно решить.

Bведение

Aктуальность темы исследования

B первые с задачами, для решения которых используются графы, я столкнулся на олимпиаде по математике. Трудности в решении этих задач объяснялись отсутствием этой темы в обязательном курсе школьной программы.

Bозникшая проблема, стала главной причиной выбора темы данной исследовательской работы.

Kак - то попалась для решения задача про зоопарк. На рис. 1 приведена его карта-схема.[6]

Рис. 1

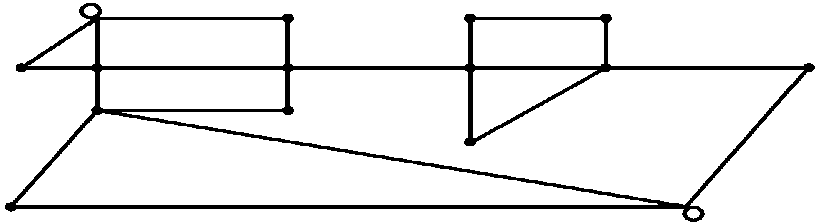
Bершины - это вход, выход, перекрестки и повороты, а линии - это дорожки, вдоль которых расположены клетки с животными. Нужно было найти маршрут, по которому экскурсовод мог бы провести посетителей, показав им всех зверей и не показав им более одного раза ни один участок пути. Эта задача меня заинтересовала. Поиск путей решения этой задачи познакомил меня с теорией графов, которая в настоящее время является очень популярной, так как с ее помощью можно довольно просто решать большой круг самых разнообразных математических задач и прикладных проблем. На языке теории графов условия задач приобретают наглядность, что упрощает их анализ. Сами решения являются простыми, и, в отличие от решений другими методами, не содержат утомительных вычислений. В настоящее время теория графов широко применяется в различных областях науки и техники. Язык графов удобен для описания многих физических, технических, химических, экономических, биологических, социальных и других систем.

Известна притча: некто давал миллион рублей каждому, кто начертит следующую фигуру (Приложение 5.). Но при вычерчивании ставилось одно условие. Требо­валось, чтобы фигура эта была вычерчена одним не­прерывным росчерком, т. е. не отнимая пера или ка­рандаша от бумаги и не удваивая ни одной линии, другими словами, по раз проведенной линии нельзя уже было пройти второй раз. [6]

Надежда стать «миллионером», решив «такую лег­кую» задачу, может заставить испортить много бумаги и потратить много времени на попытки вычертить эту фигуру, как требовалось, одним росчерком. Задача, однако, не решается, и это тем досаднее, что она не решается только «чуть-чуть»... Никак не удается про­вести только одной «последней» какой-либо линии.

С другой стороны выпуклый пятиугольник со всеми его диагоналями легко вычерчивается одним непрерыв­ным движением без повторения. Это создаёт серьёзную проблему - исследование, возможна или нет данная задача, прежде чем приниматься за её решение. Вместе с тем вопрос разрешимости или неразрешимости задачи имеет и практическое значение, в частности для того, чтобы понимать и уметь обосновывать, что не всякую предлагаемую задачу можно решить.

Я предположил, что свойство графа быть уникурсальным – есть способ определения возможности решения задач-головоломок. Отсюда,

объект исследования: уникурсальный граф как фигура, вычерчиваемая одним росчерком.

Предмет исследования: топологическое свойство графа быть уникурсальным и его использование для решения задач-головоломок.

Цель работы: определить и проверить свойство уникурсального графа и его использование для решения задач-головоломок.

B соответствии с целью определились следующие задачи:

- раскрыть понятие топологии;

- изучить вклад Л. Эйлера в развитие науки топологии;

- дать представление об уникурсальном графе и привести доказательство его - топологического свойства;

- проверить опытно-экспериментальным путем возможность использования свойства для решения задач-головоломок.

Гипотеза: не всякую предлагаемую задачу можно решить.

Методы исследования:

- поисковый метод с использованием научной и учебной литературы,

Интернета;

- исследовательский метод при решении задачи;

- практический метод при решении задачи

Глава 1

Леонард Эйлер и его вклад в развитие топологии

1.1. Топология - одна из математических наук, возникшая во второй половине XIX ст. Она из­учает те свойства геометрических фигур, ко­торые могут быть описаны с помощью поня­тия непрерывности.

Сама топология, можно сказать, началась с листа Мёбиуса. Слово это придумал Иоганн Бенедикт Листинг, профессор Гёттингенского университета, который почти в тоже время, что и его Лейпцигский коллега, предложил в качестве первого примера односторонней поверхности уже знакомую нам, единожды перекрученную, ленту. Наука эта молодая и потому озорная. Иначе не скажешь о тех правилах игры, которые в ней приняты. Любую фигуру тополог имеет право сгибать, скручивать, сжимать и растягивать – делать с ней всё что угодно, только не разрывать и не склеивать. И при этом он будет считать, что ничего не произошло, все её свойства остались неизменными. Для него не имеют никакого значения ни расстояния, ни углы, ни площади. А что же его интересует? Самые общие свойства фигур, которые не изменяются ни при каких преобразованиях, если только не случается катастрофы – «взрыва» фигуры. Поэтому иногда топологию называют «геометрией непрерывности». Она известна и под именем «резиновая геометрия», потому что топологу ничего не стоит поместить все свои фигуры на поверхность детского надувного шарика и без конца менять его форму, следя лишь за тем, чтобы шарик не лопнул. А то, что при этом прямые линии, например, стороны треугольника, превратятся в кривые, для тополога глубоко безразлично.

«Сотри случайные черты, и ты увидишь – мир прекрасен», - писал Александр Блок. Тополог всегда готов внять подобному призыву – во всех окружающих его предметах он ищет некие важные только ему одному качества. Например, непрерывность. Это ещё одно топологическое свойство. Если вы сравните схему самолётных маршрутов и географическую карту, то убедитесь. Что масштаб Аэрофлотом далеко не выдержан – скажем, Минск может оказаться на полпути от Москвы до Владивостока. И всё-таки что-то общее между географической картой есть. Москва действительно связана со Минском, а Минск – с Владивостоком. И поэтому тополог может, как угодно деформировать карту, лишь бы точки, ранее бывшие соседями, оставались одна подле другой и дальше. А значит, с топологической точки зрения круг неотличим от квадрата или треугольника, потому что их легко преобразовать один в другой, не нарушая непрерывности.

1.2. Основоположником теории графов считается Л. Эйлер. В 1736 г. им была выполнена работа, в которой содержалось решение знаменитой задачи о кёнигсбергских мостах. Идеи Эйлера, использованные им при решении этой задачи, явились фундаментом теории, впоследствии названной теорией графов. (В то время Л. Эйлер работал в Петербурге в Российской Академии наук. Термин «граф» впервые в 1936 г. использовал венгерский математик Д.Кёниг, назвав графами схемы, состоящие из множества точек и связывающих эти точки отрезков). [6]

Суть этой задачи заключается в следующем: можно ли пройти по всем мостам, изображенным на рисунке, так, чтобы на каждом из них побывать лишь один раз и вернуться к тому месту, откуда началась прогулка?

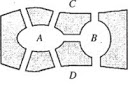
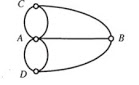
Ясно, что по условию задачи не имеет значения, как проходит путь по частям суши A, В, C, D поэтому их можно изобразить точками. A так как связи между этими частями суши осуществляются только через семь мостов, то каждый из мостов можно изобразить линией, соединяющей соответствующие вершины. B результате получается граф, изображенный на рисунке. Если бы существовал маршрут движения, удовлетворяющий условию задачи, то этот граф было бы возможно нарисовать «одним росчерком» (т.е. - без отрыва карандаша от бумаги, проводя по каждому ребру только один раз), начиная и заканчивая рисование в одной точке. Эйлером было доказано, что это невозможно. Bозникает вопрос: будет ли задача о кёнигсбергских мостах иметь решение, если отказаться от того, чтобы маршрут движения начинался и заканчивался в одной точке? В этом случае мы вновь приходим к задаче об изображении графа одним росчерком. Как будет показано ниже, граф на рисунке одним росчерком изобразить невозможно.

Глава 2

Уникурсальный граф

2.1. Большое число комбинаторных задач связано с графами.

Граф - это фигура, образованная точками плоскости, которые являются вершинами и отрезками прямых или кривых, которые соединяют эти точки и являются ребрами (р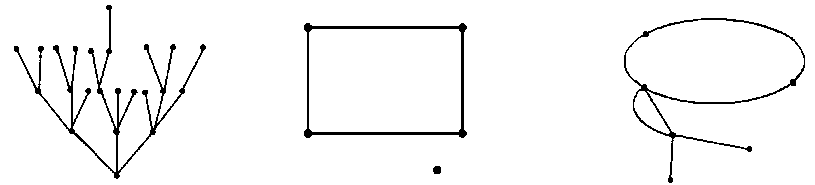ис. 1).

Рис.1

При изображении графов на рисунках или схемах отрезки могут быть прямолинейными или криволинейными; длины отрезков и расположение точек произвольны. Например, все три фигуры на рисунке 2 изображают один и тот же граф.

Рис.2

Вместо отрезков в качестве ребер графов рассматриваются так­ же кривые линии на плоскости. (Рис.3) Примерами графов могут слу­жить схемы метрополитена, же­лезных и шоссейных дорог, планы выставок и даже звёздное небо и т.д. [2]

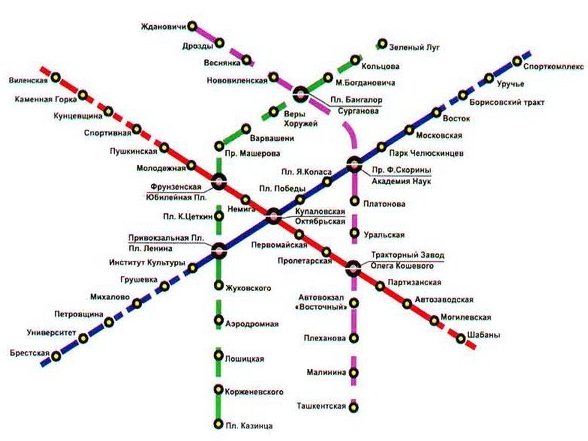
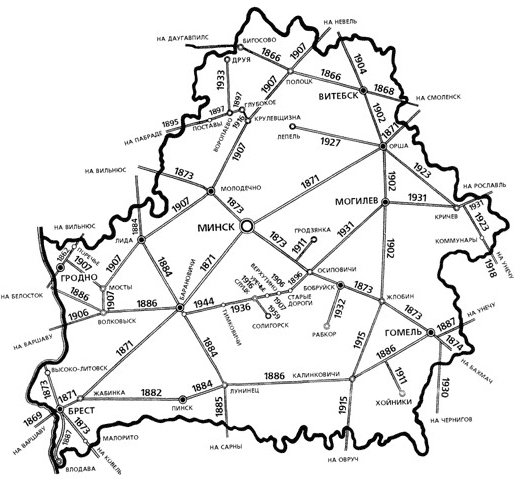Рис.3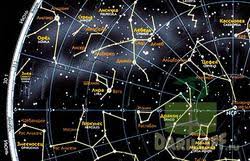

Исторически сложилось так, что теория графов зародилась в ходе решения головоломок двести с лишним лет назад.

Oдной из таких задач-головоломок была задача о кёнигсбергских
мостах, о которых мы рассказали в первой главе.

Эта задача связана с другими головоломками, суть которых в том,
чтобы обвести контур некоторой фигуры, не отрывая карандаша от бу­-
маги и не обводя ни одной линии контура дважды, то есть нарисовать
«одним росчерком».

Именно с Л. Эйлером связано одно из известных топологических свойств как непрерывность. В топологии рассматриваются графы- фигуры, состоящие из конечного числа дуг. В графе имеется несколько вершин, и некоторые из них соединены непересекающимися дугами. Граф называется уникурсальным (или эйлеровым), если его можно «нарисовать одним росчерком», т.е. пройти его весь непрерывным движением, не проходя одно и то же ребро дважды. Свойство графа быть уникурсальным является топологическим свойством[1]. Граф в том, и только в том, случае уникурсален, если в каждой его вершине, кроме, может быть, двух, сходится чётное число ребер. Имеет место следу­ющая теорема.

Теорема. Для уникурсального графа число вершин нечётного индекса (индекс вершины — число ребер гра­фа, сходящихся в данной вершине) равно нулю или двум.

Доказательство. Действительно, если граф уникурсален и его нача­ло не совпадает с концом, то начало и конец являются единственными вершинами нечётного индекса. Остальные вершины, имеют чётный индекс, так как в каждую точку мы входим и выходим из нее. Если начало совпадает с концом, то вершин с нечётным индек­сом нет. [2]

Глава 3

Oписание работы

3.1. Исследования свойств уникурсального графа я решил провести следующим образом:

3.1.1. Провести связь метода решения задач о мостах Эйлером с понятием уникурсальный граф.

Рассмотрим граф, соответствующий задаче о кёнигсбергских мостах (п. 1.2). Проверим, является ли этот граф уникурсальным. Определим чётность вершин графа. Вершина А -индекс 5, B-3,C-З и D-3. Таким образом, мы имеем четыре вершины нечетного индекса, следова­тельно, данный граф не является уникурсальным. Отсюда получаем, что во время прогулки по городу нельзя пройти по каждому из семи мостов только один раз.

Эту задачу можно было бы решить, если бы было задано обойти все мосты по два раза каждый, что привело бы к удвоению числа мостов, т.е. обращение всех вершин графа к чётному индексу.

Попробуем теперь решить другую задачу, в которой имеем два острова, соединенных между собой и берегами реки 15 мостами. (Приложение 2.) Спрашивается, можно ли за один раз обойти все мосты, не проходя ни через один более одного раза.

1) Видим количество участков, разделённых водой – 6, значит у графа 6 вершин;

2) Cосчитаем число мостов, ведущих к каждому отдельному участку – 3,5,4,8,4,6, значит у графа 2 вершины нечётного индекса и 4 вершины чётного индекса – это уникурсальный граф, следовательно можно обойти все мосты, не проходя ни через один более одного раза.

Аналогичным образом можно решить задачу с любым количеством участков, разделённых водой, и каким угодно числом и как угодно расположен­ных мостов. (Приложение 3.)

Отсюда делаем первый вывод: метод решения задач о мостах, предложенный Л.Эйлером, есть способ доказательства свойства графа, соответствующего задаче, быть уникурсальным.

3.1.2. Проверить, может ли граф иметь только одну вершину нечётного индекса

Рассмотрим уникурсальные графы (Приложение 4.) Посчитаем сумму рёбер каждого графа, сходящихся в каждой вершине: 2+3+2+3=10 2+4+2+4+2+4=18, 4+4+4+4+4=20, 2+2+4+2+2+4+2+2+4=24 и т.д.

Таким образом:

- сумма рёбер уникурсального графа всегда чётное число (две вершины нечётного индекса в сумме так же дают чётное число);

- если граф имеет одну вершину нечётного индекса, значит сумма ребер – нечётное число.

Делаем второй вывод: уникурсальный граф не может иметь только одну вершину нечётного индекса.

3.1.3. Исследование случаев разрешимости и неразрешимости задач- головоломок (фигур, вычерчиваемых одним росчерком).

Известна притча: некто давал миллион рублей каждому, кто начертит следующую фигуру (Приложение 5.). Но при вычерчивании ставилось одно условие. Требо­валось, чтобы фигура эта была вычерчена одним не­прерывным росчерком, т. е. не отнимая пера или ка­рандаша от бумаги и не удваивая ни одной линии, другими словами, по раз проведенной линии нельзя уже было пройти второй раз.

Надежда стать «миллионером», решив «такую лег­кую» задачу, может заставить испортить много бумаги и потратить много времени на попытки вычертить эту фигуру, как требовалось, одним росчерком не решается, и это тем досаднее, что она не решается только «чуть-чуть»... Никак не удается про­вести только одной «последней» какой-либо линии. Удается даже открыть секрет, что вся трудность в том, чтобы вычертить сначала одним росчерком, не повторяя линии, еще более простую фи­гуру — четырехугольник с двумя диагоналями (рис. 4). Это, ка­залось бы, уже совсем просто, а все-таки... не удается! [6]

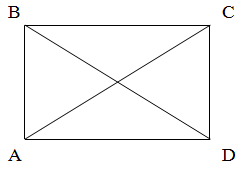Рис.4

Сомнения в невозможности решения этой задачи все-таки остаются, тем более, что фигуры, гораздо более сложные и трудные с виду, легко вычерчиваются одним росчерком, Так, например, выпуклый пятиугольник со всеми его диагоналями легко вычерчивается одним непрерыв­ным движением без повторения, причем получается фигура, представленная на р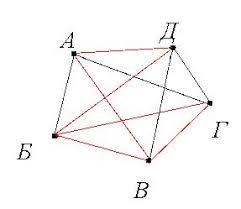ис. 5

Рис.5

То же самое легко удается со всяким многоуголь­ником с нечётным числом сторон и никак не удается с квадратом, шестиугольником и т. д. — словом, с многоугольником с чётным числом сторон.

П опробуем разобраться и показать, какую из любых данных фигур можно вычертить одним росчерком, без повторения линий, а какую нет. Сравним каждую из задач подобного рода с разобранной уже нами Эйлеровой задачей о мостах.

Возьмем четырехугольник АВСD с двумя его диагоналями, пересекающимися в Е (рис. 4). Можно ли его вычертить одним непрерывным росчерком, без повторения линий?

Точки А, В, С, D и Е мы представим себе как центры некоторых местностей, разделенных рекой, а линии, соединяющие эти точки, — как мосты, ведущие в эти местности. Что же в данном случае полу­чаем? Пять местностей, из 'которых четыре нечётные и одна чётная. Мы знаем уже, что в таком случае нельзя за один раз обойти все мосты, не переходя ни через один два раза, или, другими словами, нельзя обойти все данные точки одной непрерывной линией без повторения прежнего пути.

Случаи возможности и невозможности вычерчивания одним росчерком фигур совершенно те же, что и в задаче о мостах. Одна задача, в сущности, сводится к другой. Всякий нечётный многоугольник со всеми его диа­гоналями можно вычертить одним росчерком без по­вторения линий потому, что этот случай соответствует тому, когда данные в задаче о мостах местности все чётные.

Данный вывод одинаково при­лагается ко всякой фигуре, образована ли она пря­мыми или кривыми линиями.

Говорят, что Магомет вместо, подписи (он был неграмотен) описывал одним росчерком, состоящий из двух рогов Луны – знак. (Приложение 6.) И это понятно, потому что в данном случае мы имеем дело только с точками чётного порядка, сле­довательно, вычертить такую фигуру одним росчерком без повторения тех же линий всегда можно.

Путём практического решения задач мы пришли к выводу:

всегда можно также вычертить одним росчерком и такую фигуру, где, помимо точек чётного порядка, есть и две точки (но не более) нечётного порядка. (Приложение 7.)

Отсюда следуют выводы:

1. Если в задаче предлагается фигура, являющаяся уникурсальным графом, то задача решаема, в противном случае – не решаема;

2. Если фигура имеет только вершины чётного порядка, то начинать решение можно с любой вершины (начало решения совпадёт с концом);

3. Если фигура имеет две вершины нечётного порядка, то решение необходимо начинать с одной из них, тогда выход будет в другой.

Эти выводы мы с учителем использовали при решении задачи № 3 Замкнутые ломаные ХХI Республиканского турнира юных математиков.

Например.

Существует ли 2021-звённая ломаная, пересекающая каждое свое звено ровно 3 раза?

Ответ: не существует. Предположим противное - такая ломаная существует. Тогда суммарное число ее пересечений со своими звеньями равно 3∙2021. С другой стороны, каждой паре пересекающихся звеньев соответствуют ровно 2 пересечения ломаной своих звеньев (если звенья a и b пересекаются, то в точке пересечения этих звеньев ломаная по одному разу пересекает как звено a, так и b). Таким образом, суммарное число пересечений ломаной своих звеньев должно быть чётным. Тем самым, получено противоречие, поскольку 3∙2021 - нечётное число.

Показали как можно применить идеи Эйлера при построении определенным способом ломаных с любым количеcтвом вершин.

Мы исследовали звезды – фигуры, полученными последовательным соединением точек, количеством более двух, расположенных в определенном порядке, например, на окружности.

Простой пример – пятиконечная звезда.

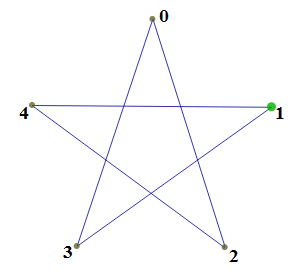
Так как форма звезды, очевидно, зависит от нумерации вершин, будем нумеровать вершины, начиная с нуля. Пятиконечная звезда имеет вершины 0, 1, 2, 3 и 4. При этом они соединены в определенном порядке. Порядок соединения определяет форму звезды. Пятиконечную звезду, изображенную на рисунке можно записать (0, 2, 4, 1, 3, 0). Начинать следует всегда с вершины 0. Номер вершины, следующей за нулевой, назовем шагом. В этих терминах звезда (0, 2, 4, 1, 3, 0) получает обозначение  [5 с ш.2.] А это и есть наша самопересекающаяся ломаная (5,2), которая каждое своё звено пересекает два раза.

Утверждение 1. Шаг должен быть взаимно простым с числом вершин n .

Пример 1. Для звезды с 6 вершинами существует единственная вырожденная форма[6 с ш.1.] , поскольку числа 2 и 3 не могут быть шагами – они не взаимно просты с 6.

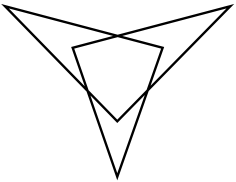
Ломаная (6,2) не существует. Это невозможно, так как у шестизвённой ломанной по крайней мере одно звено имеет 3 точки пересечения или не одного.

Благодаря заключениям Эйлера были найдены возможные формы и способы построения самопересекающихся ломаных в форме звезд.

Таким образом, узнав, что же такое уникурсальный граф, мне стало понятно, как решить задачу про зоопарк и как решать другие задачи–головоломки. Просчитав индексы всех вершин, я определил, что граф, имеет две нечётные вершины, следовательно, его можно начертить, не отрывая карандаша от бумаги, при этом движение начинаем с одной из этих нечётных вершин (вход) и заканчиваем во второй из них (выход).

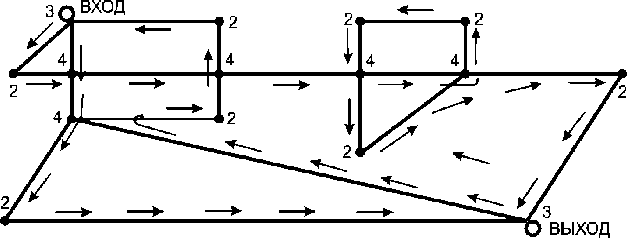
В данной задаче существует маршрут, по которому экскурсовод мог бы провести посетителей, показав им всех зверей и не показав и более одного раза ни один участок пути.

Другой задачей-головоломкой, связанной с графами и с именем Эйлера, была задача о трёх домиках и трёх колодцах. [6]

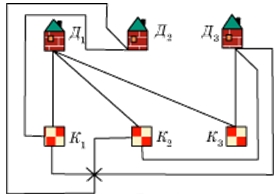
Можно ли построить три дома, вырыть три колодца и соединить тропинками каждый дом с каждым колодцем так, чтобы тропинки не пересекались?

1 решение (использую свойство уникурсальности графов). Очевидно, это задача не имеет решения. Граф на рисунке не уникурсален, так имеет более двух вершин нечётного порядка.

2 решение (используем теорему Эйлера). Для решения этой задачи воспользуемся теоремой, доказанной Леонардом Эйлером в 1752 г.

Если многоугольник разбит на конечное число многоугольников, то имеет место равенство В – Р + Г=1, где В – общее число вершин, Р – общее число ребер, Г – число многоугольников

Предположим, что это можно сделать. Отметим домики точкам Д₁ Д₂ Д₃, а колодцы точками K₁ K₂ K₃.

Каждую точку-домик соединим с каждой точкой-колодцем. Получим девять ребер, которые попарно не пересекаются.

Эти ребра образуют на плоскости многоугольник, разделенный на более мелкие многоугольники. Поэтому для этого разбиения должно выполняться соотношение Эйлера В – Р + Г = 1. Добавим к рассматриваемым граням еще одну–внешнюю часть плоскости по отношению к исходному многоугольнику. Тогда соотношение Эйлера примет вид В – Р + Г – 2, причем В = 6 и Р = 9. Следовательно, Г = 5. Каждая из пяти граней имеет, по крайней мере, четыре ребра, поскольку по условию задачи ни одна из дорожек не должна непосредственно соединять два дома или два колодца. Так как каждое ребро принадлежит ровно двум граням, то количество ребер должно быть не меньше 10, что противоречит условию, по которому их число равно 9. Полученное противоречие показывает, что ответ в задаче отрицателен: нельзя провести непересекающиеся дорожки от каждого домика к каждому колодцу.

Заключение

«Мышление начинается с удивления»,- заметил 2500 лет назад Аристотель. Наш современник Сухомлинский считал, что чувство удивления – могучий источник желания знать: “от удивления к знаниям – один шаг”. А математика замечательный предмет для удивления.

Именно это я попытался показать в своей работе, исследуя свойство уникурсального графа и его применение к решению задач- головоломок.

Проведя связь метода решения задач о мостах с понятием уникурсальный граф, мы пришли к выводу, что метод решения задач, предложенный Л.Эйлером, есть способ доказательства свойства графа, соответствующего задаче, быть уникурсальным.

Исследуя случаи разрешимости и неразрешимости задач- головоломок (фигур, вычерчиваемых одним росчерком), мы пришли к выводу, что случаи возможности и невозможности вычерчивания одним росчерком фигур совершенно те же, что и в задаче о мостах. А решение их основывается на свойстве уникурсального графа.

Таким образом, гипотеза, выдвинутая нами, подтвердилась.

Список используемых источников

1. Аммосова Н.В., Коваленко Б.Б. Использование теории графов в математическом образовании школьников, 2009 г. - 132 с.

2. Зыков А.А. Основы теории графов, 2004 г. - 664 с .

3. Мельников О.И. Занимательные задачи по теории графов, 2001 г. - 144 с.

4. Мельников О.И. Незнайка в стране графов, 2007 г. - 160 с.

5. Носов В.А. Комбинаторика и теория графов, 1999 г. - 116 с.

6. Интернет ресурсы: http://web.snauka.ru/issues/2015/12/61428,

http://pm.farfor.nt

Приложение1.

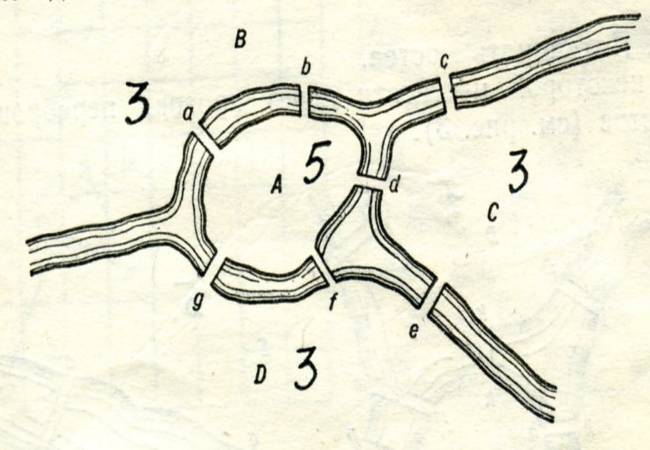Задача о 7 мостах.

Приложение 2.

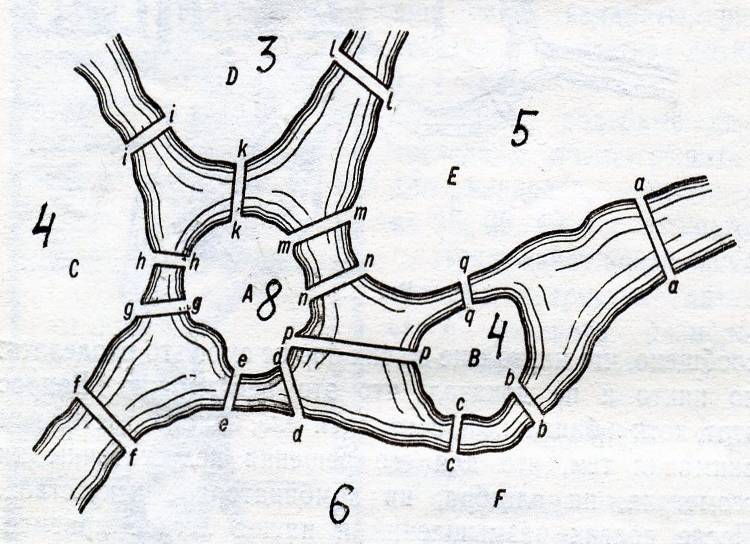Задача о 15 мостах.

Приложение3.

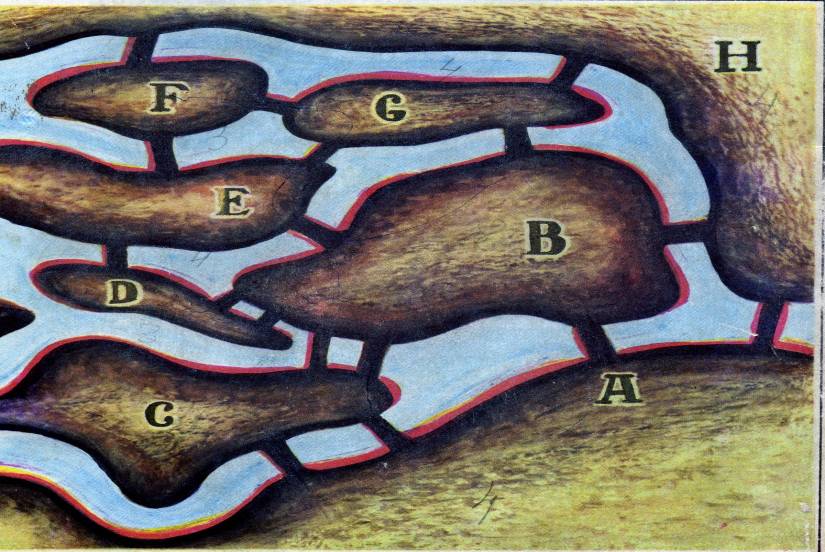
Можно ли составить маршрут прогулки так, чтобы пройти по каждому мосту только один раз?

Приложение 4.

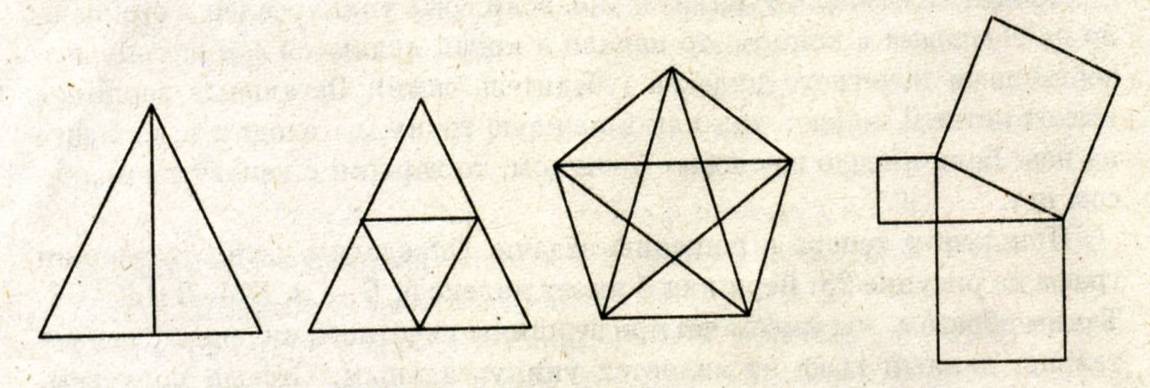
Приложение5.

Некто давал миллион рублей каждому, кто начертит эту фигуру одним непрерывным росчерком, не отрывая карандаша от бумаги не проводя по одной и той же линии дважды.

Приложение 6.

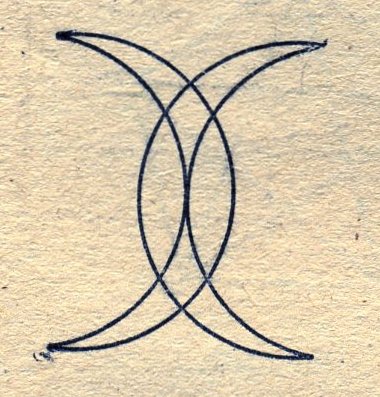
Знак, состоящий из двух рогов Луны, который Магомет описывал одним росчерком вместо подписи (он был неграмотен).

Приложение 7.

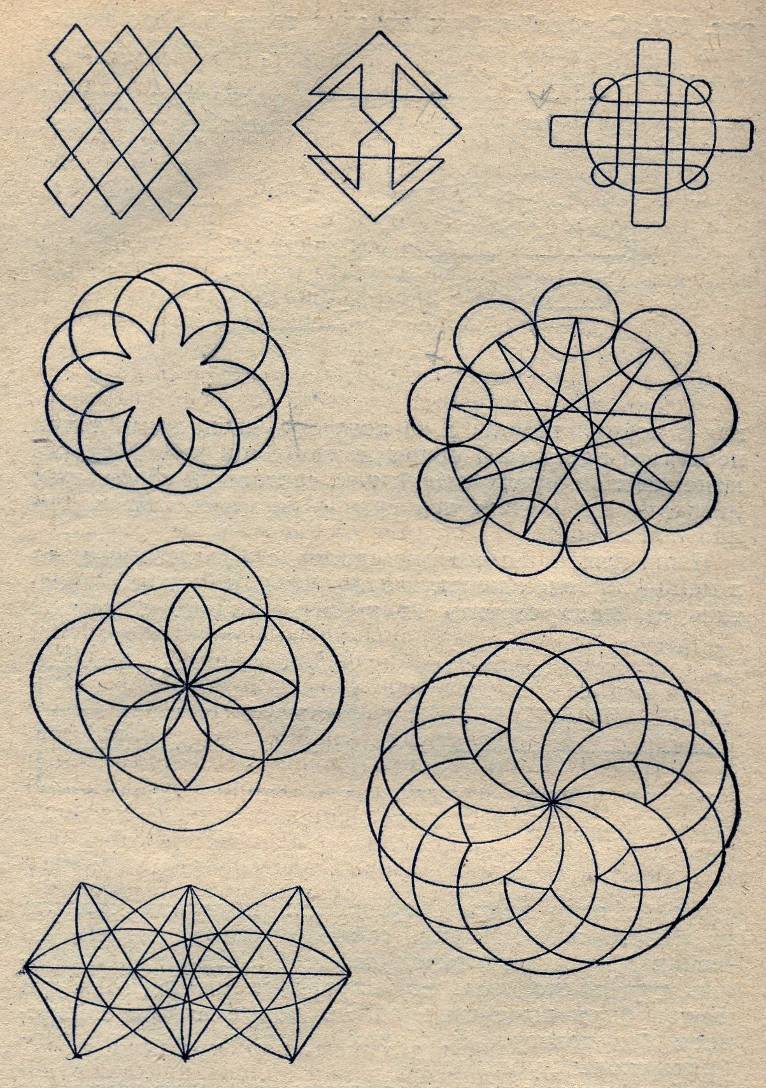
Фигуры, вычерчиваемые одним росчерком.

23