| № уро-ка | Дата по плану | Дата по факту | Название темы урока | Цели и задачи | Вид контроля |
|
|
|
|
| 1 четверть – 40 часов |
|
|
|
|
| Повторение курса математики 7-9 классов (4 ч) |
|
| 1 | 2.09 |
| Формулы сокращенного умножения. Преобразование рациональных выражений | повторение с учащимися действий с дробями, используя формулы сокращенного умножения; закрепление навыков учащихся в доказательстве рациональных тождеств. |
|
|
| 2 | 4.09 |
| Арифметический квадратный корень. Свойства квадратного корня |
|
|
| 3 | 6.09 |
| Решение рациональных уравнений |
|
|
| 4 | 8.09 |
| Решение неравенств | СР |
|
|
| Действительные числа. (16 ч.) |
|
| 5 | 9.09 |
| Натуральные и целые числа. Делимость натуральных чисел. | Знать и понимать: алгоритм Евклида условие разрешимости уравнения a+x=b в множестве натуральных чисел и операция вычитания; условие разрешимости уравнения ax=b в множестве натуральных чисел и операция деления; идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики; аксиоматику действительных чисел; роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики; принцип математической индукции Уметь: выполнять каноническое разложение числа; выполнять переход от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной; решать уравнения и неравенства с модулем (линейные, квадратные); строить простейшие графики с модулем; выполнять арифметические действия с действительными числами (точными и приближенными), сравнивать числа; применять понятия, связанные с делимостью целых чисел, при решении математических задач; применять метод математической индукции
|
|
|
| 6 | 11.09 |
| Признаки делимости. Простые и составные числа |
|
|
| 7 |
|
| Натуральные и целые числа. Деление с остатком. НОД и НОК. |
|
|
| 8 |
|
| Уравнения в целых числах. Основная теорема алгебры |
|
|
| 9 |
|
| Рациональные числа. Перевод бесконечной периодической десятичной дроби в обыкновенную. | СР |
|
| 10 |
|
| Иррациональные числа |
|
|
| 11 |
|
| Иррациональные числа |
|
|
| 12 |
|
| Множество действительных чисел. Действительные числа и числовая прямая. |
|
|
| 13 |
|
| Множество действительных чисел. Числовые неравенства. |
|
|
| 14 |
|
| Модуль действительного числа. Решение уравнений, содержащие знак модуля |
|
|
| 15 |
|
| Модуль действительного числа. Решение неравенств, содержащие знак модуля | СР |
|
| 16 |
|
| Модуль действительного числа. Ускоренные методы построения графиков с модулем |
|
|
| 17 |
|
| Обобщение. Подготовка к контрольной работе | СР |
|
| 18 |
|
| Контрольная работа №1 по теме «Действительные числа» | КР |
|
| 19 |
|
| Метод математической индукции |
|
|
| 20 |
|
| Метод математической индукции |
|
|
| Числовые функции. (12 ч.) |
|
| 21 |
|
| Числовая функция. Определение и способы задания. | Цель: обобщить и систематизировать имеющиеся у учащихся сведения о числовых функциях, углубить и расширить функциональные представления учащихся Знать и понимать: понятие числовой функции; способы задания функции; область определения; область значений; график функции, преобразование графиков функций (параллельный перенос, растяжения и сжатия вдоль осей координат, симметрия относительно осей координат и относительно прямой y=x); свойства функций (четность, нечетность; возрастание и убывание; нули функции и промежутки знакопостоянства; наибольшее и наименьшее значения, периодичность); отражение свойств функции на графике; понятие функции как соответствие между множествами; элементарные функции, их свойства и графики; функции y=[x], y={x}, обратную функцию Уметь: определять значения функции по значению аргумента при различных способах задания функции; строить графики изученных функций, выполнять преобразования графиков; описывать по графику и по формуле поведение и свойства функций; описывать и исследовать с помощью функций реальные зависимости; строить графики кусочно-заданных функций; функций, связанных с модулем; взаимообратных функций
|
|
|
| 22 |
|
| Свойства функций. Область определения. Множество значений. |
|
|
| 23 |
|
| Свойства функций. Монотонность, экстремумы, выпуклость, ограниченность, четность. |
|
|
| 24 |
|
| Свойства функций. Монотонность, экстремумы, выпуклость, ограниченность, четность. | СР |
|
| 25 |
|
| Наибольшее и наименьшее значение функции на промежутке |
|
|
| 26 |
|
| Периодические функции |
|
|
| 27 |
|
| Периодические функции | СР |
|
| 28 |
|
| Обратная функция |
|
|
| 29 |
|
| Обратная функция |
|
|
| 30 |
|
| Обобщение. Подготовка к контрольной работе | СР |
|
| 31 |
|
| Контрольная работа №2 по теме «Числовые функции» |
|
|
| Тригонометрические функции. (26ч.) |
|
| 32 |
|
| Числовая окружность. | Цель: сформировать у учащихся представления о числовой окружности на координатной плоскости; сформировать умения находить значение синуса, косинуса, тангенса и котангенса на числовой окружности; овладеть умением применять тригонометрические функции числового аргумента, при преобразовании тригонометрических выражений; овладеть навыками и умениями построения графиков функций y = sin x, y = cos x, y = tg x, y = ctg x
Знать и понимать: понятие числовой окружности; радианное измерение углов; определение синуса, косинуса любого действительного числа, связь этих определений с определениями тригонометрических функций, введенных в курсе планиметрии; соотношения между тригонометрическими функциями одного и того же аргумента (угла, числа); знаки тригонометрических функций в зависимости от расположения точки, изображающей число на числовой окружности. тригонометрические функции; синусоида, тангенсоида; свойства и графики тригонометрических функций Уметь: строить графики основных тригонометрических функций; читать по графикам их свойства; применять теоретический материал при выполнении письменных заданий Знать и понимать: арксинус, арккосинус, арктангенс, арккотангенс; математическое представление гармонических колебаний; графики гармонических колебаний; свойства и графики функций y = tg x, y = ctg x; обратные тригонометрические функции, их свойства и графики; преобразование графиков тригонометрических функций (параллельный перенос, растяжения и сжатия вдоль осей координат, симметрия относительно осей координат и относительно прямой y=x) Уметь: вычислять обратные тригонометрические функции некоторых числовых значений; строить графики основных тр. функций; строить графики функций вида y = m f(x), путем преобразования графика y = f(x); строить графики функций вида y = f(kx), путем преобразования графика функции y = f(x); описывать свойства тригонометрических функций y = tg x, y = ctg x; уметь определять период, частоту и амплитуду гармонических колебаний |
|
|
| 33 |
|
| Числовая окружность. Запись интервалов |
|
|
| 34 |
|
| Числовая окружность на координатной плоскости | СР |
|
| 35 |
|
| Синус и косинус |
|
|
| 36 |
|
| Синус и косинус | СР |
|
| 37 |
|
| Тангенс и котангенс |
|
|
| 38 | 24.10 |
| Тангенс и котангенс | СР |
|
|
|
|
| 2 четверть |
|
|
| 39 | 5.11 | 18.11 | Тригонометрические функции числового аргумента |
|
|
| 40 | 7.11 | 19.11 | Тригонометрические функции числового аргумента |
|
|
| 41 | 9.11 |
| Тригонометрические функции числового аргумента |
|
|
| 42 | 9.11 | 19.11 | Тригонометрические функции углового аргумента | СР |
|
| 43 | 11.11 |
| Функции 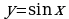 и и 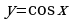 , их свойства и графики , их свойства и графики |
|
|
| 44 | 12.11 |
| Функции 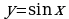 и и 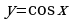 , их свойства и графики , их свойства и графики |
|
|
| 45 | 14.11 |
| Функции 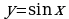 и и 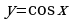 , их свойства и графики , их свойства и графики | СР |
|
| 46 | 16.11 |
| Функции 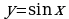 и и 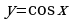 , их свойства и графики , их свойства и графики |
|
|
| 47 | 16.11 |
| Контрольная работа №3 по теме «Тригонометрические функции» | КР |
|
| 48 | 18.11 | 28.11 | Построение графиков функции 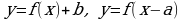 |
|
|
| 49 | 19.11 |
| Построение графиков функции 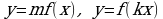 . Растяжение и сжатие вдоль осей координат . Растяжение и сжатие вдоль осей координат |
|
|
| 50 | 21.11 |
| Построение графиков функции 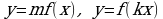 . Растяжение и сжатие вдоль осей координат . Растяжение и сжатие вдоль осей координат |
|
|
| 51 | 23.11 |
| График гармонического колебания | СР |
|
| 52 | 23.11 |
| Графики 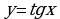 и и 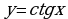 , их свойства и графики , их свойства и графики |
|
|
| 53 | 25.11 |
| Графики 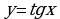 и и 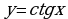 , их свойства и графики , их свойства и графики |
|
|
| 54 | 26.11 | 7.12 | Обратные тригонометрические функции |
|
|
| 55 | 28.11 |
| Обратные тригонометрические функции |
|
|
| 56 | 30.11 |
| Обратные тригонометрические функции | СР |
|
| 57 | 30.11 | 12.12 | Обратные тригонометрические функции. |
|
|
| Тригонометрические уравнения. (14 ч.) |
|
| 58 | 2.12 | 14.12 | Простейшие тригонометрические уравнения | Цель: сформировать у учащихся умение решать простейшие тригонометрические уравнения и научить обучающихся некоторым приемам решения тригонометрических уравнений и систем уравнений Знать и понимать: тригонометрическое уравнение, простейшее тригонометрическое уравнение; однородное тригонометрическое уравнение первой степени, второй степени; формулы для решения тригонометрических уравнений; графическое изображение решений тригонометрических уравнений и неравенств Уметь: решать простейшие тригонометрические уравнения и неравенства, а также применять тригонометрические преобразования к более сложным; показывать решение на единичной окружности |
|
|
| 59 | 3.12 | 14.12 | Простейшие тригонометрические уравнения |
|
|
| 60 | 5.12 | 16.12 | Простейшие тригонометрические уравнения | СР |
|
| 61 | 7.12 | 17.12 | Простейшие тригонометрические неравенства |
|
|
| 62 | 7.12 | 19.12 | Простейшие тригонометрические неравенства |
|
|
| 63 | 9.12 | 21.12 | Простейшие тригонометрические неравенства | СР |
|
| 64 | 10.12 | 21.12 | Методы решения тригонометрических уравнений |
|
|
| 65 | 12.12 | 23.12 | Методы решения тригонометрических уравнений |
|
|
| 66 | 14.12 | 24.12 | Методы решения тригонометрических уравнений | СР |
|
| 67 | 14.12 | 25.12 | Методы решения тригонометрических уравнений |
|
|
| 68 | 16.12 | 26.12 | Методы решения тригонометрических уравнений |
|
|
| 69 | 17.12 | 28.12, 28.12 | Методы решения тригонометрических уравнений |
|
|
| 70 | 19.12 | 30.12, 11.01 | Подготовка к контрольной работе | СР |
|
| 71 | 21.12 | 11.01 | Контрольная работа № 4 по теме «Тригонометрические уравнения» | КР |
|
| Преобразование тригонометрических выражений. (30 ч.) |
|
| 72 | 21.12 | 13.01 | Синус и косинус суммы и разности аргументов | Цель: выработать знания и умения, связанные с применением изученных формул тригонометрии к преобразованию тригонометрических выражений Знать и понимать: формулы, связывающие тригонометрические функции одного и того же аргумента; формулы сложения аргументов; преобразование сумм тригонометрических функций в произведение; преобразование произведений тригонометрических функций в суммы. формулы, связывающие функции аргументов, из которых один вдвое больше другого Уметь: преобразовывать сумму тригонометрических функций в произведение; преобразовывать произведение тригонометрических функций в сумму; выполнять преобразование выражения A sin x + B cos x к виду C sin (x + t); проводить преобразования числовых и буквенных выражений, включающих тригонометрические функции; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для практических расчетов по формулам, содержащим тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства
|
|
|
| 73 | 23.12 | 14.01 | Синус и косинус суммы и разности аргументов |
|
|
| 74 | 24.12 | 16.01 | Синус и косинус суммы и разности аргументов |
|
|
| 75 | 23.12 | 18.01 | Синус и косинус суммы и разности аргументов | СР |
|
| 76 | 26.12 | 18.01 | Тангенс и котангенс суммы и разности аргументов |
|
|
| 77 | 28.12 | 20.01 | Тангенс и котангенс суммы и разности аргументов |
|
|
| 78 | 28.12 | 21.01 | Тангенс и котангенс суммы и разности аргументов | СР |
|
| 79 | 30.12 | 23.01 | Формулы приведения
|
|
|
|
|
|
| 3 четверть |
|
|
| 80 | 15.01 | 25.01 | Формулы приведения |
|
|
| 81 | 17.01 | 25.01 | Формулы двойного аргумента. Формулы понижения степени. | СР |
|
| 82 | 18.01 | 27.01 | Формулы двойного аргумента. Формулы понижения степени. |
|
|
| 83 | 20.01 | 28.01 | Формулы половинного аргумента. Универсальная подстановка |
|
|
| 84 | 20.01 | 30.01 | Формулы половинного аргумента. Универсальная подстановка | СР |
|
| 85 | 22.01 | 01.02 | Преобразование суммы тригонометрических функций в произведение |
|
|
| 86 | 24.01 | 01.02 | Преобразование суммы тригонометрических функций в произведение |
|
|
| 87 | 25.01 | 03.02 | Преобразование произведения тригонометрических функций в сумму |
|
|
| 88 | 27.01 |
| Преобразование произведения тригонометрических функций в сумму | СР |
|
| 89 | 27.01 | 04.02 | Преобразование выражения 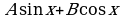 к виду к виду 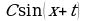 |
|
|
| 90 | 29.01 | 06.02 | Преобразование выражения 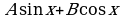 к виду к виду 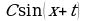 |
|
|
| 91 | 30.01 |
| Преобразование выражения 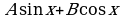 к виду к виду 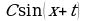 | СР |
|
| 92 | 01.02 | 8.02 | Методы решения тригонометрических уравнений |
|
|
| 93 | 03.02 | 8.02 | Методы решения тригонометрических уравнений |
|
|
| 94 | 03.02 |
| Методы решения тригонометрических уравнений | СР |
|
| 95 | 05.02 | 10.02 | Уравнения и неравенства с обратными тригонометрическими функциями |
|
|
| 96 | 07.02 | 11.02 | Уравнения и неравенства с обратными тригонометрическими функциями |
|
|
| 97 | 08.02 | 13.02 | Решение уравнений повышенной сложности |
|
|
| 98 | 10.02 | 15.02 | Подготовка к контрольной работе | СР |
|
| 99 | 10.02 | 15.02 | Контрольная работа №5 по теме «Преобразование тригонометрических выражений»
| КР |
|
| Комплексные числа 13(8 ч) |
|
| 100 | 12.02 | Перенос после темы ПРОИЗВОДНАЯ 19.04 | Комплексные числа и арифметические операции над ними | Основные цели: создать условия учащимся для: Формирования представления о комплексных числах и операциях над ними; ввести две формы записи комплексного числа. Овладением навыками и умениями выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, в простейших случаях находить комплексные корни уравнений с действительными коэффициентами. |
|
|
| 101 | 14.02 | 19.04 | Комплексные числа и координатная плоскость |
|
|
| 102 | 15.02 | 21.04 | Тригонометрическая форма записи комплексного числа |
|
|
| 103 | 17.02 | 22.04 | Комплексные числа и квадратные уравнения | СР |
|
| 104 | 17.02 |
| Комплексные числа и квадратные уравнения |
|
|
| 105 | 19.02 | 24.04 | Возведение комплексного числа в степень. Извлечение кубического корня из комплексного числа. |
|
|
| 106 | 21.02 | 26.04 | Обобщающий урок по теме «Комплексные числа» |
|
|
| 107 | 22.02 | 26.04 | Контрольная работа №6 по теме «Комплексные числа» | КР |
|
|
| Производная (38ч) |
|
| 108 | 24.02 | 17.02 | Числовые последовательности. Определение и способы задания числовых последовательностей | Знать и понимать: производная, ее геометрический и физический смысл; дифференцируемая функция; правила дифференцирования, формулы дифференцирования; алгоритм отыскания производной; уравнение касательной к графику функции; таблица производных основных элементарных функций; производная функции вида 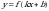 ; ; Уметь: вычислять производные элементарных функций, применяя правила вычисления производных и первообразных, используя справочные материалы; вычислять производную суммы, произведения, частного функций; находить производную сложной функции; находить уравнение касательной, координаты точек касания; уметь написать уравнение касательной к функции в заданной точке; определять угол наклона касательной
Знать и понимать: точка экстремума (максимума, минимума) функции; стационарная точка, критическая точка функции; алгоритм исследования функции на монотонность и экстремумы; алгоритм отыскания наибольшего и наименьшего значений непрерывной функции на промежутке; понятие о непрерывности функции. Уметь: исследовать функции и строить их графики с помощью производной; решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке; решать геометрические, физические, экономические и другие прикладные задачи, в том числе задачи на наибольшие и наименьшие значения с применением аппарата математического анализа |
|
|
| 109 | 25.02 | 18.02 | Числовые последовательности. Определение и способы задания числовых последовательностей |
|
|
| 110 | 27.02 | 20.02 | Предел числовой последовательности. |
|
|
| 111 | 01.03 | 22.02 | Предел числовой последовательности. Вычисление пределов. |
|
|
| 112 | 01.03 | 22.02 | Предел числовой последовательности. Вычисление пределов. | СР |
|
| 113 | .03.03 | 24.02 | Предел функции. Предел функции на бесконечности. Предел функции в точке. |
|
|
| 114 | 04.03 | 25.02 | Предел функции. Нахождение асимптот графиков элементарных функций |
|
|
| 115 | 05.03 | 27.02 | Задачи, приводящие к понятию производной |
|
|
| 116 | 07.03 | 0103 | Определение производной |
|
|
| 117 | 10.03 | 01.03 | Определение производной | СР |
|
| 118 | 10.03 | 03.03 | Вычисление производных: формулы дифференцирования |
|
|
| 119 | 12.03 | 04.03 | Вычисление производных: формулы дифференцирования |
|
|
| 120 | 14.03 | 06.03 | Вычисление производных: формулы дифференцирования |
|
|
| 121 | 15.03 | 10.03 | Вычисление производных: формулы дифференцирования | СР |
|
| 122 | 17.03 | 11.03 | Вычисление производных: понятие и вычисление производных n-го порядка |
|
|
| 123 | 17.03 | 13.03 | Вычисление производных: понятие и вычисление производных n-го порядка |
|
|
| 124 | 19.03 | 15.03 | Дифференцирование сложной функции | СР |
|
| 125 | 21.03 | 15.03 | Дифференцирование сложной функции |
|
|
| 126 | 22.03 | 17.03 | Дифференцирование сложной функции |
|
|
| 127 | 24.03 | 18.03 | Дифференцирование обратной функции |
|
|
| 128 | 24.03 | 20.03 | Дифференцирование обратной функции |
|
|
|
|
|
| 4 четверть |
|
|
| 129 | 02.04 | 22.03 | Геометрический смысл производной. |
|
|
| 130 | 04.04 | 22.03 | Уравнение касательной к графику функции. |
|
|
| 131 | 05.04 |
|
|
|
|
| 132 | 07.04 | 24.03 | Уравнение касательной к графику функции. | СР |
|
| 133 | 09.04 | 25.03 | Контрольная работа №7 по теме «Производная» | КР |
|
| 134 | 11.04 | 27.03 | Исследование функций на монотонность |
|
|
| 135 | 12.04 | 5.04 | Исследование функций на монотонность |
|
|
| 136 | 14.04 | 5.04 | Отыскание точек экстремума |
|
|
| 137 | 14.04 | 7.04 | Отыскание точек экстремума |
|
|
| 138 | 16.04 | 8.04 | Применение производной для доказательства тождеств и неравенств | СР |
|
| 139 | 18.04 | 10.04 | Построение графиков функций |
|
|
| 140 | 19.04 | 12.04 | Построение графиков функций |
|
|
| 141 | 21.04 | 12.04 | Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке |
|
|
| 142 | 21.04 | 14.04 | Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке | СР |
|
| 143 | 23.04 | 15.04 | Задачи на отыскание наибольших и наименьших значений величин |
|
|
| 144 | 25.04 | 17.04 | Задачи на отыскание наибольших и наименьших значений величин |
|
|
| 145 | 26.04 | 19.04 | Контрольная работа №8 по теме «Применение производной»
| КР |
|
|
| Комбинаторика и вероятность (10 ч) |
|
| 146 | 28.04 | 28.04 | Правило умножения. Комбинаторные задачи. Перестановки и факториалы. | Знать и понимать: правило умножения для подсчета вариантов; перестановки, факториалы; биномиальные коэффициенты; формула бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля; вероятность и статистическая частота наступления события (определения вероятности: классическое статистическое, геометрическое); формулы числа перестановок, сочетаний, размещений, решение комбинаторных задач; вероятность суммы несовместных событий, вероятность противоположного события; понятие о независимости событий; Уметь: решать практические задачи с применением вероятностных методов; решать простейшие комбинаторные задачи методами перебора, а также с использованием известных формул, вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля; вычислять вероятности событий; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характер. |
|
|
| 147 | 28.04 | 29.04 | Правило умножения. Комбинаторные задачи. Перестановки и факториалы. |
|
|
| 148 | 30.04 | 03.05. | Выбор нескольких элементов. Биномиальные коэффициенты |
|
|
| 149 | 02.05 | 03.05 | Выбор нескольких элементов. Биномиальные коэффициенты | СР |
|
| 150 | 03.05 | 05.05 | Случайные события и их вероятность |
|
|
| 151 | 05.05 | 06.05 | Случайные события и их вероятность |
|
|
| 152 | 05.05 | 08.05 | Подготовка к контрольной работе |
|
|
| 153 | 07.05 | 12.05 | Контрольная работа № 9 по теме «Комбинаторика и вероятность» | КР |
|
| Повторение (18 ч)
|
|







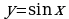 и
и 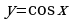 , их свойства и графики
, их свойства и графики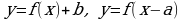
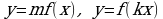 . Растяжение и сжатие вдоль осей координат
. Растяжение и сжатие вдоль осей координат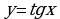 и
и 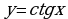 , их свойства и графики
, их свойства и графики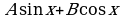 к виду
к виду 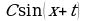
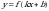 ;
;









