Карточка-консультант по теме: " Свойство четырехугольника, описанного около окружности"

Свойство четырехугольника, описанного около окружности

Если все стороны четырёхугольника касаются окружности, то он называется четырёхугольником, описанным около этой окружности, а окружность — вписанной в четырёхугольник.

Не все четырёхугольники возможно описать около окружности.

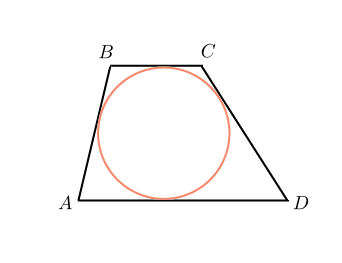
Т. Суммы длин противоположных сторон описанного около окружности четырёхугольника равны между собой.

Четырехугольник описан около окружности, значит AB+CD=BC+AD

Т. Если суммы противоположных сторон четырёхугольника равны, то в такой четырёхугольник можно вписать окружность.

Если AB+CD=BC+AD, то четырехугольник можно описать около окружности

Это свойство можно использовать и как признак для определения, в какие четырёхугольники можно вписать окружность.

Вопросы для размышления:

• В какой прямоугольник можно вписать окружность?

• В какой параллелограмм можно вписать окружность?

3. Решение задач

• Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.

P_ABCD=40

Решение:

По свойству описанного четырехугольника, AB+CD=BC+AD= P_ABCD:2=40:2=20

BC+AD= 20.

Мы помним, что средняя линия трапеции равна полусумме оснований, значит средняя линия равна 20:2=10.

Ответ: 10

• Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32.

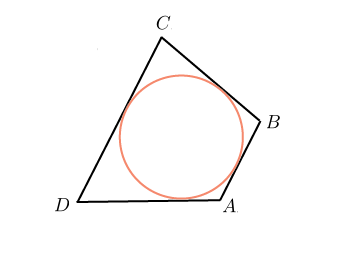AB:AD:DC=1:2:3

P_ABCD=32

Найти: большую сторону

Пусть х – одна часть, тогда AB = x, AD = 2x, а DC = 3x. По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,

AB+CD=BC+AD

x+3x=BC + 2x

BC = 2x.

Тогда P_ABCD= AB+CD+BC+AD= 8x.

8x=32

x=4,

Большая сторона DC = 3x = 12.

Ответ:12