Карточки для индивидуальной работы по ликвидации пробелов
в знаниях учащихся с ОВЗ по алгебре 7 класса
Методическая разработка – проблемно-творческой группы математиков
Руководитель: Тихонова Г.И. учитель математики МОУ «С(к)ОШ №24».
Координатор Шонохова Е.Н., методист МУ ДПО «ЦПКИМР».
Магнитогорск
 2022г.
2022г.
«Карточки для индивидуальной работы по ликвидации пробелов в знаниях учащихся с ОВЗ» (Тихонова Г.И. «С(к)ОШ №24», Нефедова Л.А. «С(к)ОШ №17», Ильичева Л.М. «С(к)ОШ №242, Беляева Е.Л. «С(к)ОШ №24», Астафьева А.Н. «С(к)ОШ №24», Даниловская О.Н. «С(К)ОШИ №4», Ишмурзина З.И. «СОШ №62)», Гаврилова И.П. «С(К)ОШ №3») - Магнитогорск. 2022- 31с.
Карточки для индивидуальной работы по ликвидации пробелов в знаниях учащихся с ОВЗ предназначен для учителей математики с целью использования в учебной деятельности.
Рекомендуются для работы с обучающимися, имеющими:
- пробелы в знаниях,
- большое количество пропусков занятий (по болезни),
- ограниченные возможности здоровья.
1. Пояснительная записка
Одной из актуальных проблем в школе остается проблема повышения эффективности учебно-воспитательного процесса и преодоление школьной неуспеваемости. Ее решение предполагает совершенствование методов и форм организации обучения, поиск новых, более эффективных путей формирования знаний у учащихся, которые учитывали бы их реальные возможности.
Карточки по математике для ликвидации пробелов в знаниях учащихся. Предупредить и ликвидировать пробелы в знаниях ученика – одна из важнейших составляющих в работе учителя, и неудовлетворительное качество этой работы ведет к накоплению у учащихся пробелов в знаниях до той степени, когда их устранение становится для ученика практически невозможным, и он переходит в разряд стабильно неуспевающих.
При этом ученику практически невозможно перейти в разряд хорошо успевающих, поскольку даже при самом добросовестном отношении к предмету он всё равно получает отрицательные оценки за ошибки, в основе которых – старые пробелы в знаниях. Чтобы осознать свои ошибки и ликвидировать их, ученик должен иметь под рукой правило, формулу или алгоритм решения.
Эту проблему помогают решить карточки-памятки, в которых отражены основные вопросы по той или иной теме, а именно прописываются: теоретический материал , алгоритм решения , помещены тренировочные задания . Иногда достаточно одного взгляда на теоретический материал, чтобы ученик «раскрутил» ту цепочку основных умений, которые в свое время, видимо, не были доведены у него до автоматизма. Если недостаточно одного взгляда на теоретический материал чтобы вспомнить нужное, значит, есть необходимость поработать с алгоритмом решения по данной теме и закрепить навыки, порешав тренировочные задания.
Содержание
Карточки
Линейные уравнения
Вычитание чисел с разными знаками
Сложение и вычитание обыкновенных дробей с одинаковыми знаменателями
Сложение и вычитание обыкновенных дробей с разными знаменателями
Умножение обыкновенных дробей
Деление обыкновенных дробей
Площадь. Площадь прямоугольника
Раскрытие скобок
Сокращение дробей
Линейные уравнения
Пропорция
Проценты
Прямая пропорциональность
Решение уравнений
Сложение чисел с разными знаками
Движение в противоположных направлениях
Движение в одном направлении
1. Карточка по ликвидации пробелов в знаниях
Тема «Системы линейных уравнений»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
1.Способ подстановки:
выразить из какого-нибудь уравнения системы одну переменную через другую; подставить в другое уравнение системы вместо этой переменной полученное выражение; решить получившееся уравнение с одной переменной; найти соответствующее значение второй переменной.
|
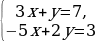
у = 7-3х -5х + 2(7-3х)=3 -5х + 14-6х=3 -5х-6х=3-14 -11х=-11 х=1 у=7-3ˑ1=7-3=4 Ответ: (1;4)
|
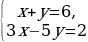
|
|
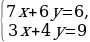 3х=9-4у х=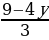 7ˑ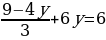 /*3 /*3
7ˑ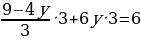 ˑ3 ˑ3 7(9-4у)+18у=18 63-28у+18у=18 -28у+18у=18-63 -10у=-45 у=4,5 х=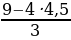 х=-3 Ответ;(-3; 4,5) |
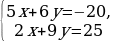
|
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
2.Способ сложения:
умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами; сложить почленно левые и правые части уравнений системы; решить получившееся уравнение с одной переменной; найти соответствующее значение второй переменной
|
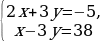 + +
3х=33 х=11 11-3у=38 -3у=27 у=-9 Ответ: (11;-9) |
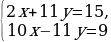
|
| 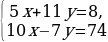
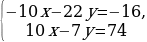
-29у=58 у=-2 10х-7·(-2)=74 10х=74-14 10х=60 х=6 Ответ: (6;-2)
| 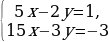
|
| 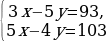 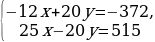
13х=143 х=11 5·11-4у=103 55-4у=103 -4у=103-55 -4у=48 у=-12
Ответ: (11; -12)
| 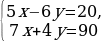
|
2. Карточка по ликвидации пробелов в знаниях
Тема «Одночлены»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
| Одночлены. Произведение числовых и буквенных множителей называется одночленом. Например: 5ab4ab2 5 и 4 – числовой множитель; ab, ab2 – буквенный множитель. Правило: чтобы привести одночлен в стандартный вид, нужно: Перемножить числовые множители и их произведение поставить на первое место: 5*4=20 перемножить степени с одинаковыми основаниями (при этом показатели степеней складываются) ab*ab2=a1+1b1+2=a2b3 5ab4ab2=20a2b3 – одночлен в стандартном виде. Числовой множитель одночлена, записанного в стандартном виде, называется КОЭФФИЦИЕНТОМ ОДНОЧЛЕНА: k=20 СТЕПЕНЬ ОДНОЧЛЕНА равна сумме степеней буквенных множителей: n=2+3=5
|
Задание: записать одночлен в стандартном виде 3a2a5bc4(-5)b2 - перемножим числовые множители, 3*(-5)=-15, поставим их произведение на 1 место, - перемножить степени с одинаковыми основаниями (a2a5bc4b2) = a2+5b1+2c4 = a7b3c4 - запишем результат 3a2a5bc45b2 = -15a7b3c4 - коэффициент, степень одночлена k=-15, n=7+3+4=14
|
Задание: записать одночлен в стандартном виде, указать коэффициент и степень одночлена. а) 4a3c3b(-7)с2а4; б)6с2(-0,8)с
|
2. Карточка по ликвидации пробелов в знаниях
Тема «Умножение одночленов. Возведение одночлена в степень»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
| Умножение одночленов:
Перемножим числовые множители. Перемножим степени с одинаковыми основаниями. Представим одночлен в стандартном виде.
Возведение одночлена в степень: 1.Взведем в степень каждый множитель. 2.Результат перемножим. 3. Представим одночлен в стандартном виде.
|
Задание: -5а2вс•4а2в4= (-5•4)( а2• а2)(в1•в4)•с= =-20а4 в5с1
Задание: (-4а2в4)2 = (-4)2• (а2)2• (в4)2=16а4в8
|
Задание1: -6х3а4•9ах=
Задание2: (-2х3у2)3= |
3. Карточка по ликвидации пробелов в знаниях
Тема «Умножение степеней с натуральным показателем»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
Чтобы умножить степени с одинаковыми основаниями надо: - основание оставить прежним, - а показатели степеней сложить.
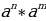 = =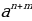
|
Пример 1
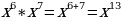
Пример 2
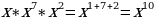
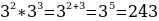
|
а) х5· х8; е) x6 ∙ x3 ∙ x7;
б) у2· у9 ; ж) m2· m5 · m4 ;
в) 2 6 · 2 4 ; з) а2· а · а4 ;
г) 2 3 · 2 3 ; и) 102· 10 · 104 ;
д) 4 · 4 2 ; к) p2· p2· p · p ·p4 ;
|
3. Карточка по ликвидации пробелов в знаниях
Тема «Деление степеней с натуральным показателем»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
Чтобы разделить степени с одинаковыми основаниями надо: - основание оставить прежним, - а из показателя степени делимого вычесть показатель степени делителя.
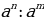 = =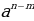
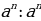 = = 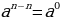
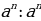 = 1 = 1
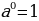
| Пример 1
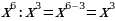
Пример 2
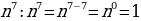
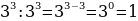
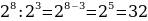
|
а) х8: х4; е) 0,58: 0,56;
б) у11: у9 ; ж) 1010: 106;
в) 4 6: 4 4 ; з) 46: 4 4 ;
г) 210: 2 5 ; и) p 20: p 14 ;
д) 6 2: 6 2 ; к) а 40: а 24 .
|
3. Карточка по ликвидации пробелов в знаниях
Тема «Возведение в степень произведение»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
Чтобы возвести в степень произведение нужно: - возвести в эту степень каждый множитель - и результаты перемножить.
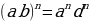
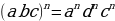
| Пример 1

Пример 2


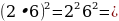 4*36= 144 4*36= 144
Пример 3


|
а)  д) ( д) (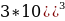
б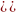 е) е) 
в) (-4 х) 4 ж) 
г) (-2аbc) 5
|
3. Карточка по ликвидации пробелов в знаниях
Тема «Возведение степени в степень»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
При возведении степени в степень нужно - основание оставить тем же, - а показатели перемножают..
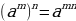
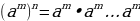
n раз
|
Пример 1
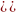
Пример 2
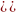 ; ;
|
а) 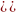
б) 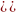
в) 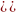
г) 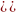 ; ;
д) 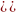
|
4. Карточка по ликвидации пробелов в знаниях
Тема «Параллельные прямые»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
| Две прямые на плоскости называются параллельными, если они не пересекаются. a, b – прямые, с – секущая. 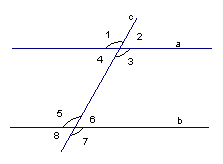
Рис. 1 Возникает много углов (1, 2, 3, 4, 5, 6, 7, 8). Эти углы важны для нас, и поэтому они имеют названия: -накрест лежащие углы: ∠3 и ∠5, ∠4 и ∠6; -односторонние углы: ∠4 и ∠5, ∠3 и ∠6; -соответственные углы: ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7.
| Задача 1: На рисунке изображен параллелограмм, назовите накрест лежащие, односторонние и соответственные углы при прямых AB//DC и секущей AD.
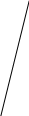 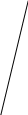   А В
  1 2
 
   3 4
   5 6 С
   D
  
8 7
Решение: При AB//DC и секущей АD -накрест лежащие углы: ∠3 и ∠5, ∠4 и ∠6; -односторонние углы: ∠4 и ∠5, ∠3 и ∠6; -соответственные углы: ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7. Так же можно рассмотреть углы при AB//DC и секущей BC.
| Задача 1: На рисунке изображен ромб, назовите накрест лежащие, односторонние и соответственные углы при прямых AB//DC и секущей AD.     
B D C А Подсказка: обозначьте углы цифрами. |
| Основные теоремы о параллельности прямых: Если накрест лежащие углы равны, то прямые параллельны. И наоборот, если прямые параллельны, то накрест лежащие углы равны.
Рис. 2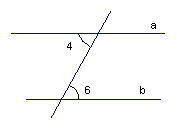
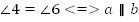
| Задача 2: Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210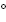 . Найдите эти углы. . Найдите эти углы. Дано: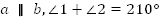 . . Найти: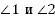 . . 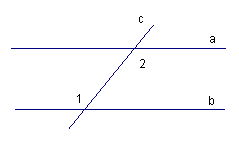
Рис. 5 Решение: Поскольку прямые a и b параллельны, то накрест лежащие углы равны. Следовательно, 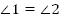 . . Тогда 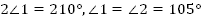 . . Ответ: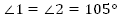 . .
| Задача 2: Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 260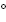 . Найдите эти углы. . Найдите эти углы.
|
Если соответственные углы равны, то прямые параллельны. И наоборот, если прямые параллельны, то соответственные углы равны. Рис. 3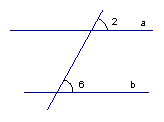
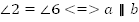
| Задача 3: Найдите все углы, образованные при пересечении параллельных прямых a и b с секущей c, если: А. один из углов равен 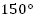 ; ; Б. один из углов на 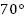 больше другого. больше другого. 
Рис. 6 А. Дано: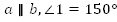 . . Найти: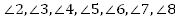 . . Решение: 1. 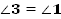 (как вертикальные); (как вертикальные); 2. 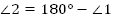 (как смежные); (как смежные); 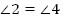 (как вертикальные); (как вертикальные);
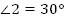 ; ;
3. 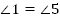 и и 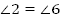 (как соответственные) (как соответственные) 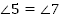 и и 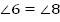 (как вертикальные) (как вертикальные)
Ответ: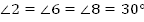 , , 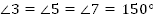 . . Б. Дано: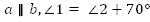 . . Найти: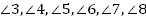 . . Решение: 1. 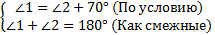 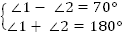 + +
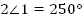 , , 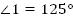 . .
Тогда 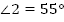 . . 2.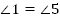 и и 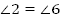 (как соответственные) (как соответственные) 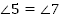 и и 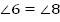 (как вертикальные) (как вертикальные)
Ответ: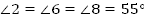 , , 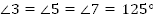 . .
| Задача 3: Две параллельные прямые пересечены третьей прямой так, что сумма двух соответственных углов равна 240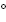 . Найдите меры всех образованных углов. . Найдите меры всех образованных углов.
|
Если сумма внутренних углов равна 1800, то прямые параллельны. И наоборот, если прямые параллельны, то сумма внутренних углов равна 1800. 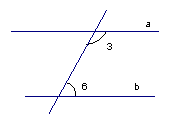
Рис. 4
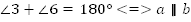
| Задача 4: На рисунке 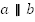 , известно, что ∠3 = 135о , известно, что ∠3 = 135о Найдите меры всех образованных углов. 
Рис. 7 Решение: Так как 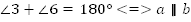 то можем найти ∠6 =180о - 135о=45о то можем найти ∠6 =180о - 135о=45о ∠3 =∠1 = 135о (вертикальные) ∠6=∠8 = 45о (вертикальные) ∠3 =∠5 = 135о (накрест лежащие) ∠6=∠4 = 45о (накрест лежащие) ∠5 =∠7= 135о (вертикальные) ∠2=∠4 = 45о (вертикальные)
| Задача 4: На рисунке 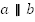 , известно, что ∠6 = 75о , известно, что ∠6 = 75о Найдите меры всех образованных углов. 
|
5. Карточка по ликвидации пробелов в знаниях
Тема «Формулы сокращенного умножения»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
| 1. Квадрат суммы двух выражений
Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
(a + b)2 = a2 + 2ab + b2 | а) (8х + 3)2 = (8х)2 + 2 ∙ 8х ∙ 3 + 32 = 64х2 + 48х +9.
б) (0,6х +4)2 =(0,6х)2 + 2 ∙ 0,6х ∙ 4 + 42 = 0,36х2 +4,8х + 16.
в) 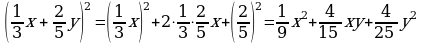
| 1.Представьте в виде многочлена:
а) (b + 3)2;
б) (2х + 5)2;
в) (9 + 8х)2;
г) (10с + 0,1у)2;
д) (4а + 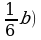 2; 2; е) (х2 + 5)2. |
| 2. Квадрат разности двух выражений
Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения.
(a - b)2 = a2 - 2ab + b2
|
а) (4х - 2)2 = (4х)2 - 2∙ 4х ∙ 2 + 32 = 16х2 - 16х +4.
б) (0,7х - 5)2 =(0,7х)2 - 2∙ 0,7х ∙ 5 + 52 = 0,49х2 - 7х + 25.
в) 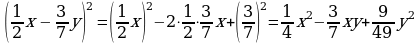
| 2.Представьте в виде многочлена:
а) (9 - у)2;
б) (у - 5)2;
в) (7у - 6)2;
г) (0,3х - 0,5у)2;
д) 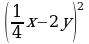 ; ;
е) (8 – у3)2. |
| 3.Разность квадратов двух выражений
Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a2 - b2 = (a - b)(a + b)
| а) 36 – х2 = 62 – х2 = (6 – х) (6 + х).
б) 49х2- 16у2 = (7х)2 – (4х)2 = (7х – 4у) (7х + 4у).
в) 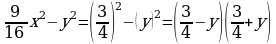 . . г) a2 b2 – c2 = (ab)2 – (c)2 = (ab – c) (ab + c).
д) с6 – х6 = (с3)2 – (х3)2 = (с3 – х3) (с3 + х3).
е) а4 – у4 = (а2)2 – (у5)2 = (а2 – у2) (а2 + у2).
ж) а4 – 9 = (а2)2 – (3)2 = (а2 – 3) (а2 +3). | 3. Разложить на множители а) c2 – z2; б) a2 – 25; в) 100 – x2; г) y2 – 0,09. д) 1,44 – a2; е) b2 -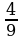 ; ; ж) 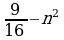 ; ; з) 0,64x2 – 0,49 y2; и) c2d2 – a2; к) a6 – b6; л) a4 – 16.
|
| 4. Умножение разности двух выражений на их сумму
Произведение разности двух выражений и их суммы равно разности квадратов этих выражений (a - b)(a + b) = a2 - b2 | а) (х – 4)(х + 4) = х2 – 42 = х2 – 16.
б) (5 – у) (5 + у) = 52 – у2 = 25 – у2.
в) (6х – 2у) (6х + 2у) = (6х)2 – (2у)2 = 36х2 – 4у2.
г) (0,6х – 0,2у) (0,6х + 0,2у) = (0,6х)2 – (0,2у)2 = 0,36х2 – 0,04у2. д) 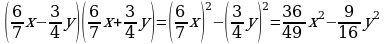
| а) (х – 9)(х + 9);
б) (8 – у) (8 + у);
в) (4х – 3у) (4х + 3у);
г) (0,5х – 0,1у) (0,5х + 0,1у);
д) 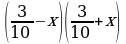 е) (х2 – 2)(х2 + 2) |
5. Карточка по ликвидации пробелов в знаниях
Тема: «Первый признак равенства треугольников»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, т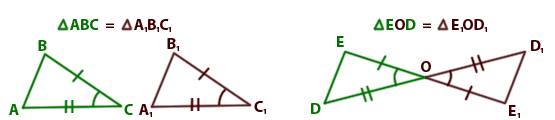 о такие треугольники равны. о такие треугольники равны. 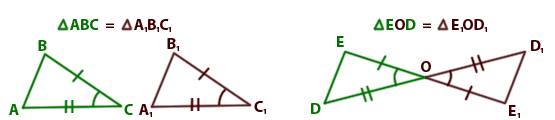
|
| ВС = В1С1 |
| | Если | АС = А1С1 | , то ∆АВС = ∆А1В1С1 | |
| ∠С = ∠С1 |
|
Первый признак равенства треугольников удобнее называть признаком равенства треугольников по двум сторонам и углу между ними
Это пригодится при решении задач
| Пример 1. На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по первому признаку равенства треугольников? Р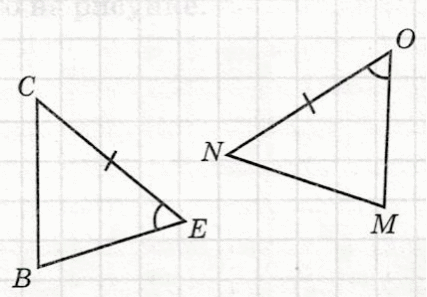 ешение: ешение: СЕ = NO по рис. ∠E = ∠O по рис. и не хватает равенства сторон: BE = MO 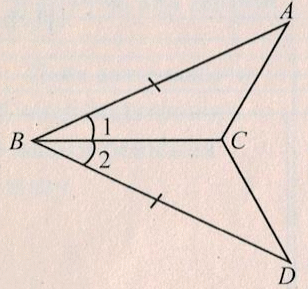
Пример 2. На рисунке AB = DB и ∠1 = ∠2. Докажите, что ∆ABC = ∆DBC. Решение: 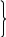 ВА = BD по усл. задачи ВА = BD по усл. задачи
∠1 = ∠2 по усл. задачи ⇒∆ABC = ∆DBC ВС – общая ч.т.д.
П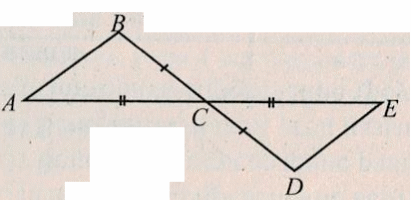 ример 3. По данным рисунка докажите, что ример 3. По данным рисунка докажите, что ∆ABC = ∆ЕDC Решение: АС = СЕ ВС = СD ∠АСВ = ∠ЕСD – вертикальные, значит по I признаку ∆ABC = ∆ЕDC. ч.т.д. |
1) На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по первому признаку равенства треугольников?
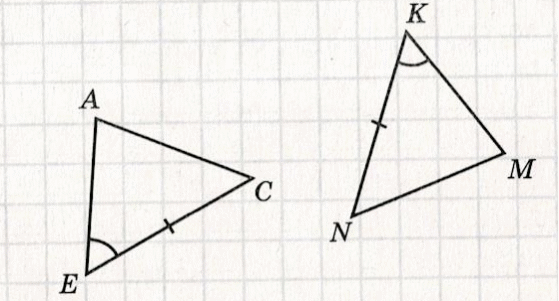
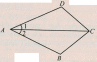
2) На рисунке AD = АB и ∠1 = ∠2. Докажите, что ∆ADC = ∆АBC. Найдите углы ADC и АCD, если ∠АВС = 1080, ∠АСВ = 320.
3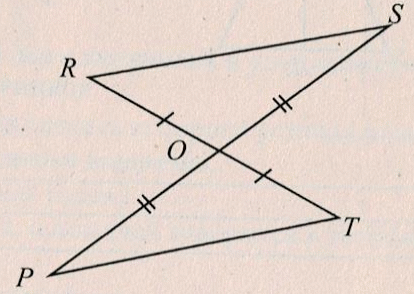 ) По данным ) По данным рисунка докажите, что ∆OSR = ∆OPT
|
5. Карточка по ликвидации пробелов в знаниях
Тема: «Второй признак равенства треугольников»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 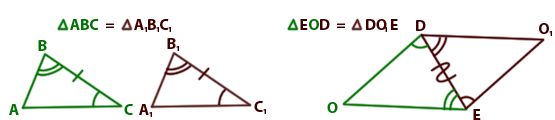
|
| ∠В = ∠В1 |
| | Если | ∠С = ∠С1 | , то ∆АВС = ∆А1В1С1 | |
| ВС = В1С1 |
|
Второй признак равенства треугольников удобнее называть признаком равенства треугольников по стороне и двум прилежащим углам
Это пригодится при решении задач
Вертикальные углы равны Биссектриса – луч, делящий угол пополам | П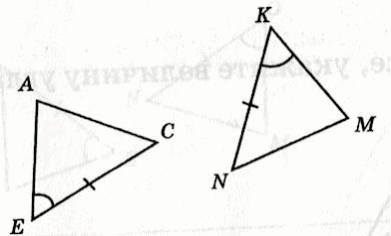 ример 1. На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников? ример 1. На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников? Решение: ЕС = КN по рис. ∠E = ∠К по рис. и не хватает равенства прилежащих углов: ∠С = ∠N 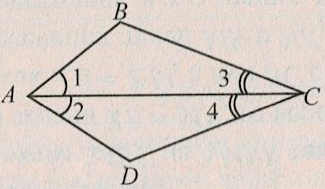
Пример 2 На рисунке ∠1 = ∠2 и ∠3 = ∠4. Докажите, что ∆ABC = ∆АDC. Решение: 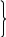  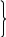 ∠1 = ∠2 по усл. задачи ∠1 = ∠2 по усл. задачи
∠3 = ∠4 по усл. задачи ⇒∆ABC = ∆DBC АС – общая 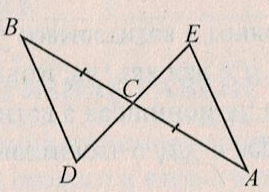
Пример 3 На рисунке ∠А = ∠В и АС = СВ. Докажите, что ∆BCD = ∆АCЕ. Решение: ∠А = ∠В и АС = СВ (по усл. задачи), ∠ВСD = ∠ЕСА – вертикальные. Значит ∆BCD = ∆АCЕ по II признаку. |
1 ) На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников? ) На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников?
2) На рисунке ∠1 = ∠2, АD – биссектриса. Д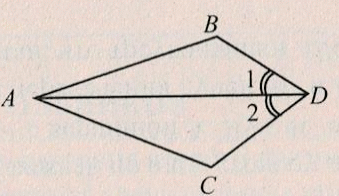 окажите, что ∆ADB = ∆АDC. окажите, что ∆ADB = ∆АDC.
3) Докажите равенство треугольников АВЕ и DСЕ, если АЕ = ЕD, ∠А = ∠D. Найдите стороны треугольника АВЕ, если DЕ = 4 см, DС = 3 см, ЕС = 5 см. 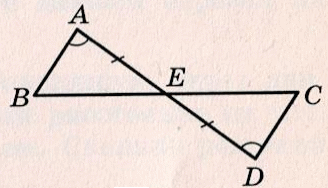
|
Карточка по ликвидации пробелов в знаниях
Тема: «Третий признак равенства треугольников»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
|
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
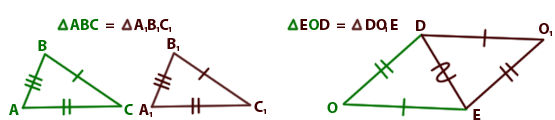
|
| АВ = А1В1 |
| | Если | ВС = В1С1 | , то ∆АВС = ∆А1В1С1 | |
| АС = А1С1 |
|
Третий признак равенства треугольников удобнее называть признаком равенства треугольников по трём сторонам.
Это пригодится при решении задач
Биссектриса – луч, делящий угол пополам В равнобедренном треугольнике боковые стороны равны
| Пример 1. На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по третьему признаку равенства треугольников? Решение: АВ = МР по рис. ВС = РК по рис. и не хватает равенства третьих сторон: СА= КМ 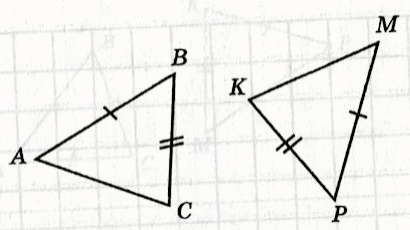
Пример 2. На рисунке треугольники ВDЕ и СDЕ – равнобедренные СЕ = ВD. Докажите, что ∆BDЕ = ∆CЕD Решение:  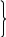 СЕ = ВD по усл. задачи СЕ = ВD по усл. задачи
С D = ВЕ – боковые стороны равнобедренных треугольников и DЕ – общая сторона. D = ВЕ – боковые стороны равнобедренных треугольников и DЕ – общая сторона. Значит ∆BDЕ = ∆CЕD по III признаку.
П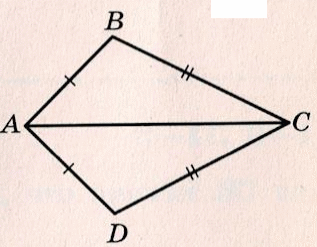 ример 3. На рисунке АВ = АD, ВС = DС. Докажите, что луч АС – биссектриса ∠ВАD ример 3. На рисунке АВ = АD, ВС = DС. Докажите, что луч АС – биссектриса ∠ВАD Решение: ∆АBС = ∆АDC по III признаку (АВ = АD, ВС = DС по условию и АС – общая) Значит ∠ВАС = ∠ DАС ⇒ луч АС – биссектриса угла ВАD. |
1) На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по третьему признаку равенства треугольников? 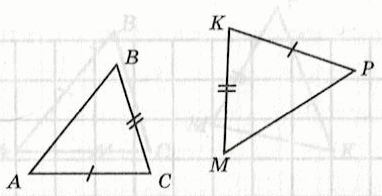
2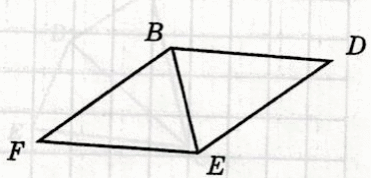 ) На рисунке треугольники ВDЕ и FBЕ – равнобедренные ВD = FЕ Докажите, что ∆BDЕ = ∆FBЕ ) На рисунке треугольники ВDЕ и FBЕ – равнобедренные ВD = FЕ Докажите, что ∆BDЕ = ∆FBЕ
3) На рисунке DЕ = DК, СЕ = СК. Докажите, что луч СD – биссектриса угла ЕСК. 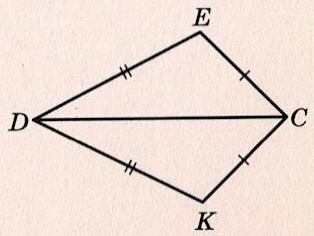
|
6. Карточка по ликвидации пробелов в знаниях
Тема «Функции»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
| Вычисление значений функции по формуле
Формула позволяет для любого значения аргумента (х) находить соответствующее значение функции (у) путем вычислений. . Чтобы вычислить значение функции (у) по ее формуле, необходимо в формулу вместо значения аргумента (х) поставить данное значение аргумента и вычислить полученное числовое выражение. Его значение и будет являться значением функции (у)
Результаты вычислений удобно записывать в виде таблице, поместив в верхней строке значения аргумента, а в нижней строке соответствующее значения функции:
|
Функция задана формулой у=2х+7. Найдите значение функции, соответствующее значению аргумента, равному 5; -20; 3,5;
Если х=5, то у= 2 · 5 + 7 = 17,
Если х= -20, то у= 2 · (-20) + 7 = - 40 +7 = = - (40-7) = -33
Если х= 3,5, то у= 2 ·3, 5 + 7 = 14 Результаты можно записать в таблицу:
|
1. Функция задана формулой у=3х-7. Найдите значение функции, соответствующее значению аргумента, равному 3; -30; 5,5;
2. Функция задана формулой у= -4х. Заполни пустые клетки таблицы
|
6. Карточка по ликвидации пробелов в знаниях
Тема «Функции»
| Теоретический материал | Задания по образцу | Задания для самостоятельной работы |
| Вычисление значения аргумента по значению функции.
Подставим в формулу функции вместо у заданное значение функции. Получим уравнение с переменной х, решив его, найдем значение аргумента х.
При решении уравнений вспомни и используй свойства, которые ты знаешь:
1. Если в уравнении перенести слагаемые из одной части в другую, изменив его знак, то получится уравнение, равносильное данному. 2. Если обе части уравнения умножить или разделить на одно и тоже отличное от нуля число, то получится уравнение, равносильное данному
|
Функция задана формулой у=2х+7. Найдите значение аргумента (х), при котором значение функции (у) равно 17, -33
Подставим в формулу функции вместо у заданное значение функции 17. Получим уравнение с переменной х 17 = 2 х + 7, 17-7 = 2 х, 10 = 2х, х= 10 : 2 , х = 5 Значит , у = 17, при х = 5
Аналогично поступаем, если у = -33
-33= 2 х + 7, -33 -7 = 2х, -40 = 2х, х = -40: 2, х = - 20 Значит, у= -33, при х = -20
|
Функция задана формулой у=3х -7. Найдите значение аргумента (х), при котором значение функции (у) равно 2, -4
|
Ответы
| Задания для самостоятельной работы |
|
| № 1. Карточка «Системы линейных уравнений» 1. Способ подстановки
|
|
| 1 | (4;2) |
|
| 2 | (-10;5) |
|
| № 1. Карточка «Системы линейных уравнений» 2. Способ сложения
|
|
| 1 | (2;1) |
|
| 2 | (-0,6;-2) |
|
| № 2. Карточка по ликвидации пробелов в знаниях «Одночлены» |
|
| 1. | -28а7с5в |
|
| 2. | -4,8с3 |
|
| №2. Карточка «Умножение одночленов. Возведение одночлена в степень»
№2. Карточка «Умножение одночленов. Возведение одночлена в степень» №2. Карточка «Умножение одночленов. Возведение одночлена в степень»
|
|
| 1 | -54х3а5 |
|
| 2 | -8х9у6 |
|
| №3. Карточка «Деление степеней с натуральным показателем» |
|
| 1. | а) 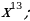 б) б) 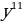 ; в) ; в) 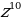 ; ; 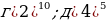 ; е) ; е) 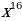 ; ж) ; ж) 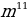 ; з) ; з) 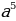 ; и) ; и) 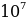 ; к) ; к) 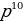 .2 .2 |
|
| №3. Карточка «Возведение в степень произведение» |
|
| 2. | а) 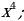 б) б) 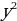 ; в) ; в) 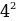 ; ; 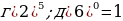 ; е) ; е) 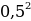 ; ж) ; ж) 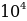 ; з) ; з) 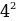 ; и) ; и) 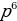 ; к) ; к) 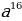 . . |
|
| №3. Карточка Возведение в степень произведение» |
|
| 3. | а) 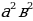 ; б ; б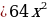 ; в) ; в) 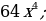 г) г) 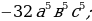 д) 27000; е) -8 д) 27000; е) -8 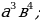 ж) ж) 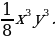 |
|
| №3. Карточка «Возведение степени в степень» |
|
| 4. | а)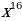 ; б ; б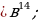 в) в) 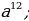 г) г) 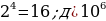 . . |
|
| №4. Карточка «Параллельные прямые»
|
|
|
 

  
  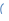 
 


При AB//CD и секущей AD образуются углы -накрест лежащие углы: ∠3 и ∠5, ∠4 и ∠6; -односторонние углы: ∠4 и ∠5, ∠3 и ∠6; -соответственные углы: ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7. |
|
| 2. | 130о |
|
|  3. Пусть ∠1 + ∠5 = 240о, тогда ∠1 = ∠5=120о. Отсюда, ∠1 = ∠3=120о, ∠5 = ∠7=120о (вертикальные), ∠5 = ∠3=120о (накрест лежащие). Найдем ∠4 +∠5 = 180о, значит ∠4 =180о-∠5=180о-120о=60о. Отсюда, ∠4=∠2=60о (вертикальные),∠4=∠6=60о(накрест лежащие), а ∠6=∠8=60о (вертикальные).
|
|
| 4.  Решение: Так как 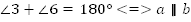 то можем найти ∠3 =180о - 75о=105о то можем найти ∠3 =180о - 75о=105о ∠3 =∠1 = 105о (вертикальные) ∠6=∠8 = 75о (вертикальные) ∠3 =∠5 = 105о (накрест лежащие) ∠6=∠4 = 75о (накрест лежащие) ∠5 =∠7= 105о (вертикальные) ∠2=∠4 = 75о (вертикальные)
|
|
|
№5. Карточка «Формулы сокращенного умножения |
|
| 1 | а) b2+6b+9; б) 4х2+20х+25; в) 81+144х + 64х2; г) 100с2+2су +0,01 у2; д) 16а2 +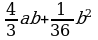 ; е) x4+10x2+25. ; е) x4+10x2+25. |
|
| 2 | а) 81 – 18у + у2; б) у2 – 10 у +25; в) 49у2 – 84у + 36; г) 0,09 х2 - 0,3 ху + 0,25 у2; д) 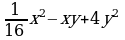 ; ; е) 64 – 16у3 + у6. |
|
| 3 | а) (c – z) (c + z); б) (a – 5) (a + 5); в) (10 – x)(10 + x); г) (y – 0,3)(c + z); д) (1,2 – а) (1,2 + а); е) 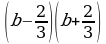 ; ; ж) 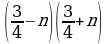 ; з) (0,8 х – 0,7у) (0,8 х + 0,7у); и) (cd - a) (cd + a); к) (a3 – b3) (a3 + b3); л) (a4 – 4) (a4 + 4). ; з) (0,8 х – 0,7у) (0,8 х + 0,7у); и) (cd - a) (cd + a); к) (a3 – b3) (a3 + b3); л) (a4 – 4) (a4 + 4). |
|
| 4 | а) х2 – 81; б) 64 – у2; в) 16х2 – 9у2; г) 0,25х2 – 0,01у2; д) 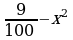 ; е) х4 – 4 . ; е) х4 – 4 . |
|
| №5. Карточка «Первый признак равенства треугольников»
|
|
| 1 | EA = KM
|
|
| 2 |
AD = АB по усл. задачи ∠1 = ∠2 по усл. задачи ⇒ ∆ADC = ∆АBC. AС – общая А так как треугольники равны, то при наложении они полностью совместятся. ∠ADC = ∠ABC = 1080 ∠ACD = ∠ACB = 320
|
|
| 3 |
RO = TO по усл. задачи SO = PO по усл. задачи ⇒∆ABC = ∆DBC ∠ROS = ∠TOP - вертикальные
|
|
| №5. Карточка «Второй признак равенства треугольников»
|
| ВЕ = МО |
|
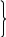 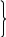 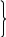 ∠1 = ∠2 по усл. задачи ∠1 = ∠2 по усл. задачи
∠BAD = ∠CAD т.к AD - биссектриса ⇒∆ADB = ∆АDC АВ – общая |
|
 AE = ED по усл. задачи AE = ED по усл. задачи
∠A = ∠D по усл. задачи ⇒ ∆АВЕ = ∆DСЕ. ∠AEB = ∠DEC - вертикальные А так как треугольники равны, то при наложении они полностью совместятся. AB = DC = 3 см, AE = DE = 4см, BE = EC = 5 см.
|
| №5.Карточка «Третий признак равенства треугольников»
|
| 1 |
AB = PM
|
| 2 | 
ВD = FE по усл. задачи ED = ВF – боковые стороны равнобедренных треугольников ⇒ ∆BDЕ = ∆FBЕ DЕ – общая сторона |
| 3 | 
DE = DK, по условию СE = СK по условию ∆СDE = ∆CKD DС – общая А так как треугольники равны, то при наложении они полностью совместятся. Значит ∠ECD = ∠ KCD ⇒ луч СD – биссектриса угла ECK.
|
| №6. Карточка « Вычисление значений функции по формуле»
|
|
| 1. | Задание 1.
| х | 3 | -30 | 5, 5 | | у | 2 | -97 | 9, 5 |
|
|
| 2 | Задание 2.
|
|
| 3 | Задание 3. У = 2, при х = 3 У = - 4, при х = 1
|
|
2
A
3
C
1
6
4
7
5
8
D





 2022г.
2022г.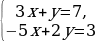
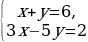
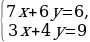
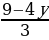
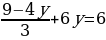 /*3
/*3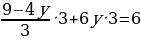 ˑ3
ˑ3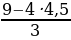
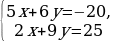
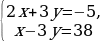 +
+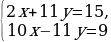
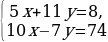
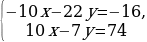
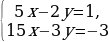
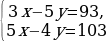
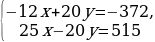
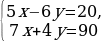
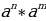 =
=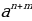
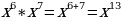
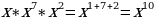
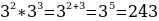
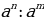 =
=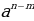
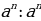 =
= 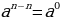
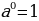
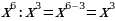
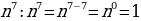
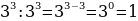
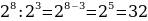
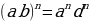
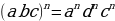

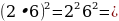 4*36= 144
4*36= 144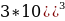
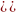 е)
е) 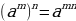
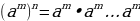

























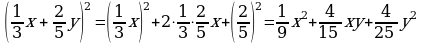
 2;
2;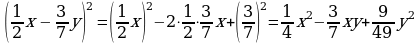
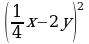 ;
;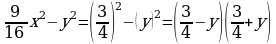 .
. ;
;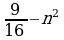 ;
;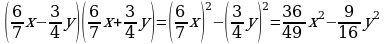
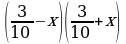
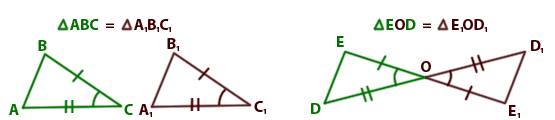 о такие треугольники равны.
о такие треугольники равны. ешение:
ешение: 
 ВА = BD по усл. задачи
ВА = BD по усл. задачи ример 3. По данным рисунка докажите, что
ример 3. По данным рисунка докажите, что 

 ) По данным
) По данным 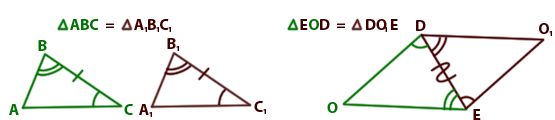
 ример 1. На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников?
ример 1. На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников?

 ) На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников?
) На рисунке помечены равные элементы двух треугольников. Какое равенство нужно добавить, чтобы треугольники были равны по второму признаку равенства треугольников? окажите, что ∆ADB = ∆АDC.
окажите, что ∆ADB = ∆АDC. 


 D = ВЕ – боковые стороны равнобедренных треугольников и DЕ – общая сторона.
D = ВЕ – боковые стороны равнобедренных треугольников и DЕ – общая сторона.  ример 3. На рисунке АВ = АD, ВС = DС. Докажите, что луч АС – биссектриса ∠ВАD
ример 3. На рисунке АВ = АD, ВС = DС. Докажите, что луч АС – биссектриса ∠ВАD
 ) На рисунке треугольники ВDЕ и FBЕ – равнобедренные ВD = FЕ Докажите, что ∆BDЕ = ∆FBЕ
) На рисунке треугольники ВDЕ и FBЕ – равнобедренные ВD = FЕ Докажите, что ∆BDЕ = ∆FBЕ
 б)
б)  ; в)
; в) 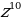 ;
; 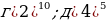 ; е)
; е) 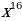 ; ж)
; ж) 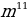 ; з)
; з) 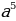 ; и)
; и) 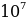 ; к)
; к) 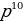 .2
.2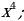 б)
б) 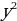 ; в)
; в) 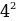 ;
; 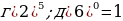 ; е)
; е) 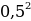 ; ж)
; ж) 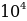 ; з)
; з) 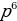 ; к)
; к) 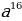 .
.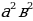 ; б
; б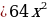 ; в)
; в) 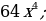 г)
г) 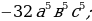 д) 27000; е) -8
д) 27000; е) -8 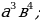 ж)
ж) 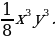
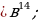 в)
в) 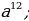 г)
г) 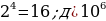 .
.









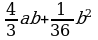 ; е) x4+10x2+25.
; е) x4+10x2+25.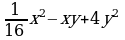 ;
; 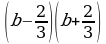 ;
;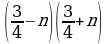 ; з) (0,8 х – 0,7у) (0,8 х + 0,7у); и) (cd - a) (cd + a); к) (a3 – b3) (a3 + b3); л) (a4 – 4) (a4 + 4).
; з) (0,8 х – 0,7у) (0,8 х + 0,7у); и) (cd - a) (cd + a); к) (a3 – b3) (a3 + b3); л) (a4 – 4) (a4 + 4).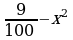 ; е) х4 – 4 .
; е) х4 – 4 .  AE = ED по усл. задачи
AE = ED по усл. задачи