Карточки по алгебре по теме "Логарифмы" для слабоуспевающих обучающихся 10 класс

Карточка 1.

Образец решения заданий к карточке 1.

1. Найдите логарифм числа 64 по основанию 4.

Решение: log₄64 = 3, так как 4³ = 64. Ответ: 3

2. Найдите число x , если log₅x = 2

Решение: log₅x = 2, x = 5² (по определению логарифма), x = 25. Ответ: 25.

3. Вычислить: log₃1/ 81 = x,

Решение: log₃1/81 = x, 3^x = 1/81, x = – 4. Ответ: – 4.

4. Вычислить: 5^log ₅⁴

Решение: 5^log₅⁴ = 4, по основному логарифмическому тождеству а^log_a^b = b. Ответ: 4.

№ 1. Найдите логарифм

1). числа 8 по основанию 2.

2). числа 1/ 27 по основанию 3.

3). числа 81 по основанию 3.

№ 2. Найдите число x:

4). log₃x = – 1 5). log 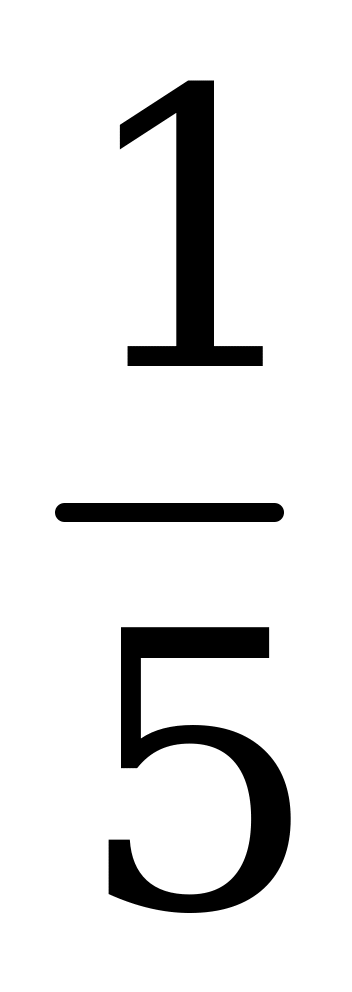x = 0 6). log _x27 = 3

№ 3. Вычислите:

7). log₄16 8). log ₅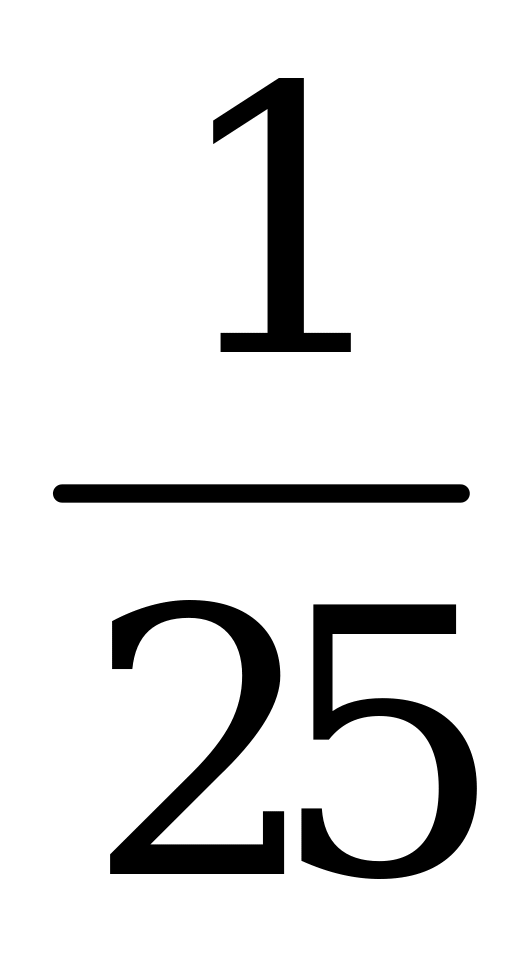 9). log 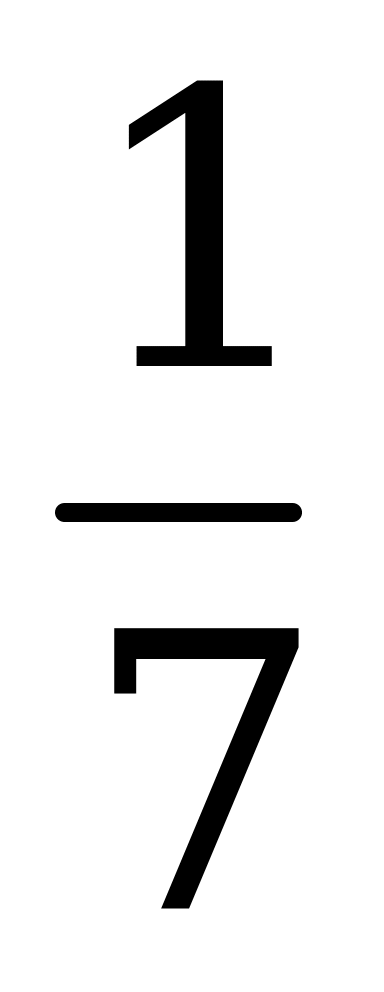49 10). log _р р

11). log₆ 1 12). log₉3 13). 2^log₂⁴ 14). 10 ^{l g100}

15). (1/2)^log_1/2¹ 16). 0,3^log_0,3² – 5.

Карточка 2.

Образец решения заданий к карточке 2.

1. Вычислить: log₆12 + log₆3

Решение: log₆12 +log₆3 = log₆(12∙ 3) = log₆36 = = log₆6² = 2. Ответ: 2.

2. Вычислить: log₅250 – log₅2.

Решение: log₅250 – log₅2 = log₅(250/2) = log₅125 = 3.

3. Вычислить: 27^log₃²

Решение: 27^log₃² = 3^3log₃² = 3^log₃⁸ = 8. Ответ: 8.

1. Вычислите: log₂16 + log₂2

2. Вычислите: log₁₂36 + log₁₂4

3. Вычислите: log₂7 – log₂7/16

4. Вычислите: log₃27/a², если log₃ a = 0,5

5. Вычислите: 4^2log₄³

6. Вычислите: (1/2)^4log_1/2³

7. Вычислите: log_0,39 – 2log_0,310

8. Вычислите: log₁₂9/144 – log₁₂9

9. Определите верное равенство:

1) log₃24 – log₃8 =16; 2) log₃15 + log₃3 = log₃5; 3) log₅5³ = 2; 4) log₂16² = 8.

10. Определите верное равенство:

1) 3log₂4 = log₂ (4∙3); 2) 3log₂3 = log₂27; 3) log₃27 = 4; 4) log₂2³ = 8.

11. Найдите значение выражения: log₃6 + log_1/32