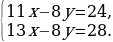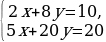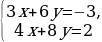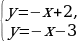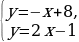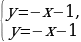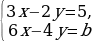Работа с картотекой поможет индивидуализировать учебный процесс для слабых учащихся без излишнего упрощения материала, позволит осуществить целенаправленную работу по формированию универсальных учебных действий, по развитию «западающих» параметров, а также по проектированию траектории индивидуального развития учеников.
Просмотр содержимого документа
«Картотека учебных форм и видов учебной работы по алгебре в 7 классе»
Картотека учебных форм и видов учебной работы
по алгебре в 7 классе
Подростковый возраст является ответственным этапом обучения. В этом возрасте ученик должен хотеть учиться, уметь учиться и верить в свои силы. Однако, в реальности некоторые дети теряют уверенность в себе, так как им не всё удается сделать из того, что другие дети делают без особых усилий. Основная задача учителя в работе с подростками – создание оптимальных условий для раскрытия и реализации возможностей каждого ученика.
Задача учителя состоит в том, чтобы создать условия для учеников из группы риска развиться до среднего уровня, учащимся, успевающим на «3» обеспечить переход на продуктивный уровень обучаемости. Необходимо построить учебный процесс так, чтобы помочь каждому обучающемуся раскрыть себя, сделать хоть небольшой, но шаг вперед.
Для помощи учителю с подбором заданий и способов учебной деятельности, необходимых для учеников 7 класса, составлена картотека заданий по всем темам учебного предмета «Алгебра»:
1. Выражения, тождества, уравнения.
2. Функции.
3. Степень с натуральным показателем.
4. Многочлены.
5. Формулы сокращённого умножения.
6. Преобразование целых выражений. Разложение многочлена на множители.
7. Системы линейных уравнений.
Работа с картотекой поможет индивидуализировать учебный процесс для слабых учащихся без излишнего упрощения материала, позволит осуществить целенаправленную работу по формированию универсальных учебных действий, по развитию «западающих» параметров, а также по проектированию траектории индивидуального развития учеников.
Тема 1. Выражения, тождества, уравнения.
| № темы | № задания | Текст задания | Этапы урока или д/з |
| У | От | Об | Д | Д/З |
|
|
| Познавательные УУД |
|
|
|
|
|
| 1 | 1 | Вместо звездочки поставь знак “+” или “–”, а вместо точек – числа:
а) (*5) + (*7) = 2;
б) (*8) – (*8) = (*4)–12;
в) (*9) + (*4) = –5;
г) (–15) – (*…) = 0;
д) (*8) + (*…) = –12;
е) (*10) – (*…) = 12. |
|
|
|
| + |
|
| 2 | Из данных уравнений выбери те, для которых число –12 является корнем: 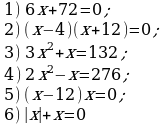
|
| + |
|
|
|
|
| 3 | Составь уравнения, равносильные уравнению:
а) х – 7 = 5;
б) 2х – 4 = 0;
в) х –11 = х – 7;
г) 2(х –12) = 2х – 24. |
|
|
|
| + |
|
| 4 | | Путешественник плыл против течения на моторной лодке 3 часа. Обратно он вернулся на плоту. Сколько времени он затратил на обратный путь, если собственная скорость лодки 20 км/ч, а скорость течения реки 2 км/ч? 1) Внесите данные условия задачи в представленную таблицу: | | Названия величин | Против течения | По течению | | Скорость движения (км/ч) |
|
| | Время движения (ч) |
|
| | Пройденный путь (км) |
|
|
| | 2) Прочитайте вопрос задачи и введите переменную. 3) Составьте уравнения для решения задачи и решите его. 4) Проверьте полученный результат. |
|
| + |
|
|
|
|
| 5 | Соедините стрелками выражение и допустимые значения переменной этого выражения:
| Выражение: |
| Допустимые значения переменной: | | 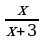 |
| 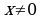 | | 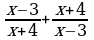
|
| 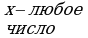
| | 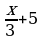 |
| 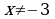
| | 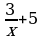 |
| 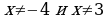
| | 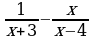
|
| 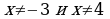
| | 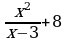 |
| 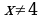
| | 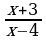 |
| 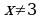
|
|
|
| + |
|
|
|
|
| Коммуникативные УУД | У | От | Об | Д | Д/З |
|
| 6 | Объясни вычисления: 1) 3,27 – 6,5 – 2,5 + 1,73 = (3,27 + 1,73) + ( – 6,5 – 2,5) = = 5 + ( – 9) = – 4; 2) 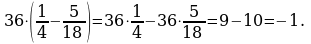
|
| + |
|
|
|
|
| 7 | Закончи предложение: 1. Для любых чисел а и в верны равенства:_________________ 2. Для любых чисел а, в и с верны равенства:_______________ 3. Распределительное свойство гласит:____________________ 4. Из переместительного и сочетательного свойств сложения следует:_______________________ 5. Из переместительного и сочетательного свойств умножения следует:_______________________ | + |
|
|
|
|
|
| 8 | Какие из приведенных ниже уравнений являются линейными? (ответ обосновать)
| + |
|
|
|
|
|
| 9 | Составьте две текстовые задачи, решение которых описывалось бы с помощью уравнения х + 3х + 5х = 270 |
|
|
|
| + |
|
| 10 | Составьте задачу по краткой записи её условия:
| Названия величин | Первый велоси-педист | Второй велоси-педист |
| | Скорость движения (км/ч) | 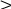
|
|
на 1 км/ч | | Время движения (ч) | 1,5 | 2 |
| | Пройденный путь (км) |
|
|
всего 12 км |
|
| + |
|
|
|
|
|
| Регулятивные УУД | У | От | Об | Д | Д/З |
|
| 11 | Вычисли наиболее рациональным способом: 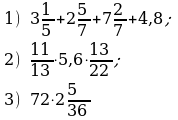
|
| + |
|
|
|
|
| 12 | Расставьте скобки так, чтобы, преобразуя левую часть, можно получить правую: 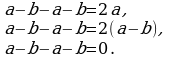
|
|
|
|
| + |
|
| 13 | Работа с текстом учебника (Алгебра, 7класс / под редакцией Ю.Н. Макарычева) по теме «Уравнение с одной переменной». План: 1. Выделите в тексте главные смысловые части. 2. Найдите по тексту ответы на вопросы: а) Какое уравнение называется линейным? б) Что называется корнем уравнения? в) Что значит решить уравнение? г) Какие бывают случаи решения линейного уравнения? д) Сколько решений может иметь линейное уравнение? 3. Найдите в тексте учебника разъяснение того, как решается: а) линейное уравнение; б) задача с помощью линейного уравнения; 5. Найдите в Интернет-ресурсах понятие «уравнение». Найдите исторические факты о том, «как люди научились решать уравнения». 6. Найдите в литературе, Интернет-ресурсах примеры задач, решаемых с помощью уравнений. | + |
|
|
|
|
|
| 14 | Проверь, правильно ли решено уравнение, если нет, то найди и исправь ошибки. 4 · (х – 5) = 12 – х
4х – 5 = 12 – х
4х + х = 12 – 5
5х = 7 │:5
х = 1,4 Ответ: 1,4. |
|
|
| + |
|
|
| 15 | Расшифруйте данные математические модели в соответствии с каждой из данных ситуаций. Математические модели: 1) a + b = 30 2) a = 3b 3) a = b + 15 4) a – b = 17 5) a : 5 = b Ситуации: Турист a км прошел пешком и b км проплыл на плоту. За конфеты заплатили a рублей, а за печенье – b рублей. В классе a девочек и b мальчиков. В стаде a овец и b коров. |
| + |
|
|
|
Тема 2. Функции.
| 2 |
| Познавательные УУД | У | От | Об | Д | Д/З |
|
| 16 | Функция задана графиком: 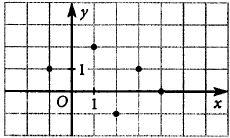
Задайте эту функцию таблицей:
| + |
|
|
|
|
|
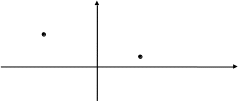
| 17 | Графиком функции служит прямая, проходящая через точки А и В. Постройте этот график и с его помощью заполните таблицу:
| 
|
|
|
|
|
|
|
| у |
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
1 |
|
|
|
| В |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| 0 | 1 |
|
|
|
|
|
|
|
|
|
| х | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| + |
|
|
|
|
|
| 18 |
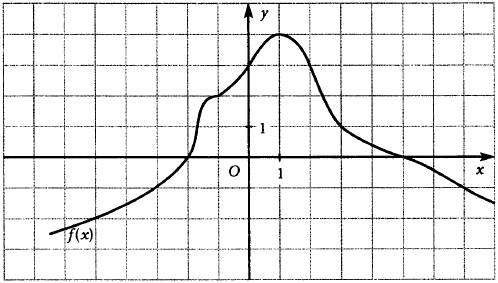
1) Чему равно значение функции при значении аргумента, равном 5? 2) Найдите значение аргумента, при котором значение функции равно 4? 3) Какое значение принимает аргумент, если значение функции равно 0? 4) Каково значение функции, если аргумент равен –1? | + |
|
|
|
|
|
| 19 | Дана функция у = – 0,5х + 10. Заполните пропуски: 1) График функции – _______________________. 2) Угол наклона графика функции к положительному направлению оси Ох – _______________________, т.к. _______________________. 3) График пересекает ось ординат в точке (___; ___). |
|
|
| + |
|
|
| 20 | Заполни текст с пропусками слов: Прямой пропорциональностью называется функция, которую можно задать формулой вида_________, где х _______ переменная, к ____________ число. График прямой пропорциональности представляет собой__________, проходящую через ______________. Чтобы построить график функции у=кх, достаточно найти координаты ___________ точки графика этой функции, отличной от___________________. При к 0 график прямой пропорциональности расположен в __________ координатных четвертях. При к0 график прямой пропорциональности расположен в __________ координатных четвертях.
|
| + |
|
|
|
| 2 |
| Коммуникативные | У | От | Об | Д | Д/З |
|
| 21 | Представлены 5 графиков: 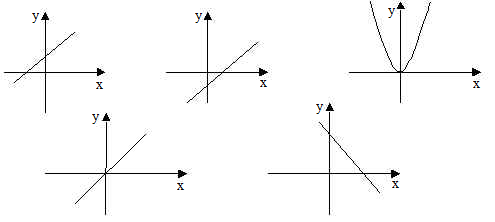
1. График какой функции лишний? Объяснить почему. 2. На каком рисунке изображен график прямой пропорциональности? Ответ объяснить. 3. На каком рисунке коэффициент k в уравнении линейной функции отрицателен? Ответ объяснить. 4. На каком рисунке свободный член b в уравнении линейной функции отрицателен? Ответ объяснить. |
| + |
|
|
|
|
| 22 | На рисунке изображен график движения туристов во время похода. Используя график, ответьте на вопросы. 1) На какое расстояние от турбазы удалились туристы? 2) Через сколько часов после начала похода туристы вернулись на турбазу? 3) На каком расстоянии от турбазы был сделан первый привал? 4) Сколько времени шли туристы от первого привала до второго? 5) Сколько времени длился второй привал? 6) Сколько времени туристы затратили на обратный путь? 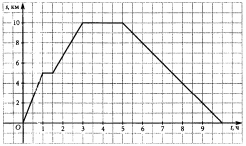
| + |
|
|
|
|
|
| 23 | На рисунке изображен график движения автобуса. Задайте вопросы товарищу по этому графику. 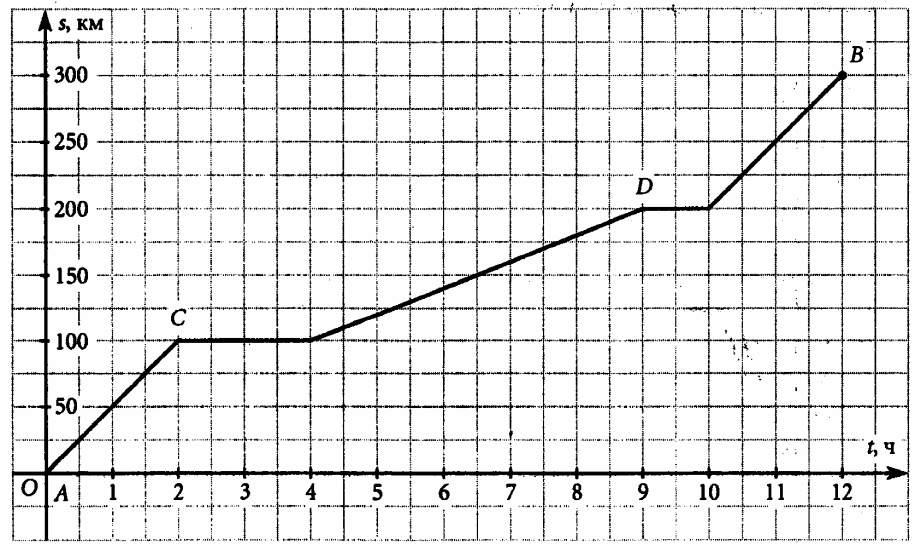
|
|
|
|
| + |
|
| 24 | Функция задана формулой вида y = kx + b. Расскажите о роли коэффициента b. • Как расположены прямые с одинаковыми коэффициентами b? • Как расположены прямые с разными коэффициентами b? |
|
| + |
|
|
|
| 25 | Функция задана формулой вида y = kx + b. Расскажите о роли коэффициента k: • Что можно сказать об угле наклона графика к оси абсцисс? • Как расположены прямые с одинаковыми коэффициентами при х? • Как расположены прямые с разными коэффициентами при х? |
|
| + |
|
|
| 2 |
| Регулятивные | У | От | Об | Д | Д/З |
|
| 26 | Рассмотрите чертежи и ответьте на вопросы. 1) На каких чертежах изображены графики линейных функций? 2) На каких чертежах изображены графики линейных функций, у которых угловой коэффициент больше нуля? 3) На каких чертежах изображены графики линейных функций, у которых угловой коэффициент равен нулю? 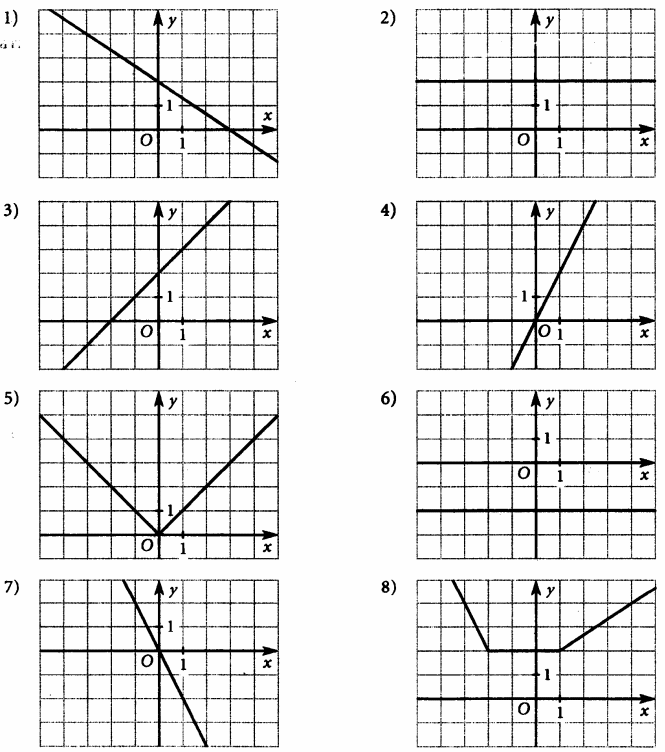
|
|
|
| + |
|
|
| 27 | Представлены три графика: у = 0,5х + 2; у = 1,5х; у = – х – 1; 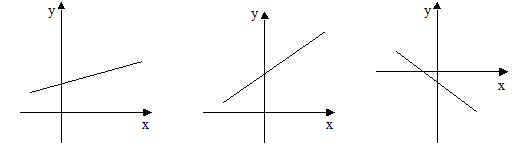
Ученик допустил ошибку при построении графика одной из функций. На каком рисунке эта ошибка? Ответ объяснить. |
|
| + |
|
|
|
| 28 | На рисунке изображены графики функций: у = 3х; у = –3х; у = х – 3; 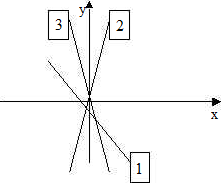
Под каким номером изображен график функции у = –3х? |
|
| + |
|
|
|
| 29 | Дана функция у = – 0,5х + 10. Изобразите схематично график этой функции. Задайте формулой функцию, график которой будет проходить через точку (0; 0) параллельно данному. |
|
|
| + |
|
|
| 30 | Найдите отличительные черты графиков прямой пропорциональности и линейной функции. |
|
|
|
| + |
Тема 3. Степень с натуральным показателем.
| 3 |
| Познавательные УУД | У | От | Об | Д | Д/З |
|
| 31 | Установите соответствие между словесной и аналитической моделями свойств степени: | Словесная модель | Аналитическая модель | | 1. умножение степеней с одинаковым основанием 2. степень с нулевым показателем 3. определение степени 4. возведение степени в степень 5. возведение в степень произведения 6. возведение в степень частного 7. возведение в степень 1 8. деление степеней с одинаковым основанием 9. возведение (– 1) в четную степень
| А. (ab)n =an.bn Б. an: am = an-m , где а ≠ 0 В. (a /b)n = an /bn , где b ≠ 0 Г. 1n = 1 Д. (an)m= anm Е. a0 = 1 Ж. ( –1)n =1, если n – четное З. an .a m = an+m И. an = a.a.a …a, где n множителей а |
| + |
|
|
|
|
|
| 32 | Запишите ответ в виде степени с основанием С и вы узнаете фамилию и имя великого французского математика, который первым ввел понятие степени числа.
|
| + |
|
|
|
|
| 33 | Из предложенных записей выберите ту, при которой равенство будет верным, и впишите её в соответствующие ячейки таблицы.
| 94–2; 34+2; 14:2; 342; 34–2; 34:2 | | 342 = |
|
|
|
| | 34:2 = |
|
|
|
| | (34)2 = |
|
|
|
|
|
|
| + |
|
|
|
| 34 | Из карточек собрать таблицу степеней 2, 3, 5.
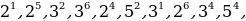
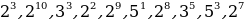
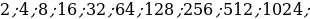
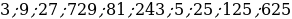
| + |
|
|
|
|
|
| 35 | Найти значение переменной, при котором верно равенство 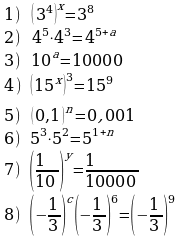
|
|
|
| + |
|
| 3 |
| Коммуникативные | У | От | Об | Д | Д/З |
|
| 36 | Выполняя задания на преобразование выражений, содержащих степени, ученик допустил ошибки. Ваша задача найти ошибки, исправьте их и объясните причину её появления. 1). 5 ∙ 5 ∙ 5 ∙ 5 = 45, (-3)2 = -3 ∙ 3 = -9, 71 =1, 00 = 1.
2). 23 ∙ 27 = 221, 23 ∙ 27= 410, 23 + 27 = 210, 230 : 210 = 23.
3). (2х)3 = 2х3, (а3)2 = а9, (а2)3 ∙ (а4)2 = (а6)5 = а30. |
| + |
|
|
|
|
| 37 | И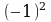 сключи лишнее, объясни своё решение. сключи лишнее, объясни своё решение.  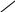 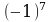  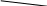 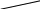 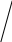 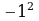 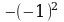 -1 -1 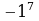 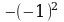
|
|
| + |
|
|
|
| 38 | Вычислите: 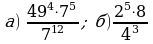 Объясните решение заданий. |
|
| + |
|
|
|
| 39 | Составить кроссворд по теме. |
|
|
|
| + |
|
| 40 | Найдите исторические сведения о возникновении степени числа и подготовьте сообщение к уроку. |
|
|
|
| + |
| 3 |
| Регулятивные | У | От | Об | Д | Д/З |
|
| 41 | Подумайте, чем можно заменить *? 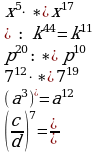 |
| + |
|
|
|
|
| 42 | Восстановите пропуски: anam =an+m a = 1 an ·bm=(ab) an am = an-m (-1)n = -1 anm = an/ = (a/b)n, b≠0 | + |
|
|
|
|
|
| 43 |
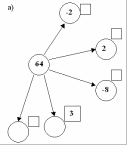 Представьте 64 в виде степени с основанием 2; -2; -8. Куб какого числа равен 64? Существует ли еще какой-нибудь способ представления 64 в виде степени с натуральным показателем? Если да, то назовите его. Представьте 64 в виде степени с основанием 2; -2; -8. Куб какого числа равен 64? Существует ли еще какой-нибудь способ представления 64 в виде степени с натуральным показателем? Если да, то назовите его. |
|
| + |
|
|
|
| 44 | 
|
|
|
|
| + |
|
| 45 | Покажите с помощью стрелки, равно ли значение выражения нулю, положительному числу или отрицательному: 
|
|
|
| + |
|
| 1. | С5∙С3 | 6. | С7 : С5 |
| 2. | С8: С6 | 7. | (С4)3 ∙С |
| 3, | (С4)3 | 8. | С4∙ С5∙ С0 |
| 4. | С5 ∙С3 : С6 | 9. | С16 : С8 |
| 5. | С14∙ с | 10. | (С3)5 |
| Р | Ш | М | Ю | К | Н | А | Т | Е | Д |
| С8 | С5 | С1 | С40 | С13 | С12 | С9 | С15 | С2 | С22 |
Тема 4. Многочлены.
| 4 |
| Познавательные УУД | У | От | Об | Д | Д/З |
|
| 46 |
| Выражения | Вопросы | | 1) 8sbs13
2) 11ax – 1,5x7x
3) d8
4) 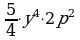 5) –13c5
6) 6(a + b)2
7) mm2 + 5n4 + 25
8) 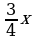
9) 16
10) 7x2a4 – x3y + 4dx + 8
11) 2x + 4 + 3,8x | – Что называется одночленом?
– Сколько одночленов записано на доске?
– Сколько одночленов стандартного вида?
– Назовите коэффициент одночлена имеющего наибольшую степень.
– Назовите коэффициент одночлена имеющего наименьшую степень.
– Какие вопросы вы могли бы задать классу? |
| + |
|
|
|
|
|
| 47 | Соединить линиями многочлены с соответствующими им способами разложения на множители 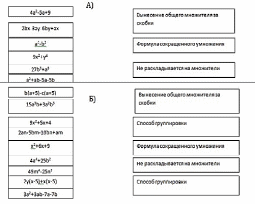
|
| + |
|
|
|
|
| 48 | Вычислите значения выражений и узнайте: а) в какое время у человека наивысшая работоспособность; б) в какое время у человека наибольшее утомление; в) когда необходимо прекращать всякую деятельность.
а) 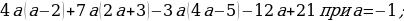 б) 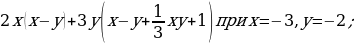 в) 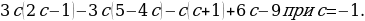 |
|
|
|
| + |
|
| 49 | Вставьте пропущенные слагаемые
а) (4а – 3)(2а + 5) = 8а2 +…. – 6а – … …. . . . = б) (3х – 5)(5х +4) = 15х2 + …. – 25х – ……. = в) (2а – 4)(3а+8) = 6а2 + …. – 12а – …. . . . =
|
|
| + |
|
|
|
| 50 | Восстановите порядок выполнения действий при разложении многочлена на множители способом группировки:
| Чтобы разложить многочлен на множители способом группировки, нужно | 1 |
| вынести общий множитель (в виде многочлена) за скобки
| | 2 |
| сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель
| | 3 |
| вынести в каждой группе общий множитель (в виде одночлена) за скобки |
|
| + |
|
|
|
| 4 |
| Коммуникативные | У | От | Об | Д | Д/З |
|
| 51 | Найдите ошибку и объясните её причину: 1) 3х (х – 3) = 3х2 – 6х; 2) 2х + 3ху = х (2 + у); 3) а6 – а2 = а2 (а2 – 1); 4) х(а + с) – 2 (а + с) = (а + с)(х + 2); 5) (6а23а + 11) – (– 3а – а3 + 7) = 6а2 – 3а + 11 –3а + а3 –7 = = а3 + 6а2 + 18 . |
| + |
|
|
|
|
| 52 | Верно ли решено? (провести стрелки и проверить) (5х + у)(3х – у) = 15х2 – 5ху + 3ху – у2 (2х – у)( х + у2) = 2х2 + 2ху2 – ух – у3 (х2 – у)(х2 + у) = х4 + х2у – ух2 – у2 (х – у)(х + у) = х2 + ху – ху – у2 = х2 – у2 | + |
|
|
|
|
|
| 53 | Выполните действия. Какие правила необходимо знать для выполнения этих примеров? а) (4x – 3y) + (3x – 4y); б) (5a – 7b) – (a – 5b); в) 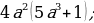 г) (4 – 3а) (5 – 2а). |
|
|
| + |
|
|
| 54 | Сформулируйте задание: 1) 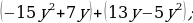 2) 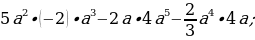 3) 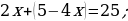 4) 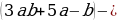 5) 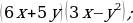 6) 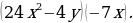 |
|
| + |
|
|
|
| 55 | Составить и провести информационную программу «Вести» по теме «Умножение многочленов». |
|
|
|
| + |
| 4 |
| Регулятивные | У | От | Об | Д | Д/З |
|
| 56 | Запишите в клетки каждого квадрата такие выражения, чтобы их сумма в каждом столбце, строке и каждой диагонали была равной «магическому» выражению, записанному в треугольнике. 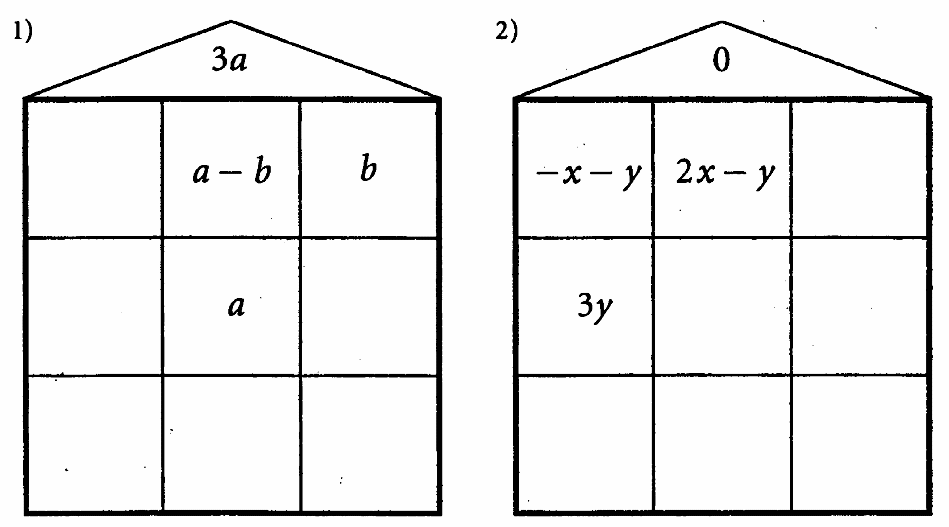 |
| + |
|
|
|
|
| 57 | Выпишите только те выражения, в которых нужно умножить многочлен на многочлен и выполните действия: (a + 3)(a + 2) 2a ∙ (a + 2) a – 10(a + 3) (4а – 3)(6 –3а) c + 2a(a – 3) (5 + a³) + a³ – 2 (n² – 8) ∙ 7n – 2 (5 + a³) (5 + a³) | + |
|
|
|
|
|
| 58 | Вместо значка * запишите такой одночлен, чтобы получившийся многочлен стандартного вида не содержал переменную а: (3а – 11 – 5а ) + ( 17 – 8а + 23 + * ) |
|
| + |
|
|
|
| 59 | Вместо квадратиков запишите такие выражения, чтобы полученный многочлен можно было разложить на множители. 1) аb + 8а +  + 72 + 72 2) 2ху – 4 +  + +  3) 9а2b – аb + 9а –  |
|
|
| + |
|
|
| 60 | Верно ли утверждение, определение, свойство? Одночленом называют сумму числовых и буквенных множителей. Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена. Целое выражение, которое содержит произведение чисел и букв, называют одночленом. Сумма показателей степеней всех букв входящих в одночлен называемый степенью одночлена. Одинаковые или отличающиеся друг от друга только коэффициентами, называют подобными членами. Алгебраическая сумма нескольких одночленов называется одночленом. В результате умножения многочлена на одночлен получается одночлен. В результате умножения одночлена на многочлен получается многочлен. Многочлен, в котором отсутствуют подобные члены и каждый из них одночлен стандартного вида называется многочленом стандартного вида. Чтобы раскрыть скобки, перед которыми стоит знак «+», скобки надо опустить, сохранив знак каждого члена, который был заключен в скобки. Когда раскрываем скобки, перед которыми стоит знак «–» , скобки опускаем, и знаки членов, которые были заключены в скобки, меняют на противоположные
|
|
|
| + |
|
Тема 5. Формулы сокращённого умножения.
| 5 |
| Познавательные УУД | У | От | Об | Д | Д/З |
|
| 61 | Заполните пропуски : 1) у2 – 100 = (у –…) (у + …)
2) 36 а2 – 25 = (…а – 5) (…а + 5)
3) (9 х2 – 16 у2 ) = (3х…4у) (3х … 4у)
4) (64 р2 – 81 к2 ) = (8 р – ….) (8р + ….). Карточки с пропущенными выражениями: 6, 10, 9к, 6, 10, 9 к, + , – . |
| + |
|
|
|
|
| 62 | Запишите на математическом языке: Квадрат суммы двух выражений с и у. Произведение суммы двух выражений а и у и неполного квадрата разности. Сумму выражений x и y. Разность квадратов двух выражений h и a. Квадрат первого выражения минус удвоенное произведение первого и второго выражений плюс квадрат второго выражения. Квадрат разности выражений b и c. Удвоенное произведение m и n. Разность кубов двух выражений. Произведение разности двух выражений и их суммы. | + |
|
|
|
|
|
| 63 | Для каждого выражения из первого столбца подберите тождественно равное ему во втором: | 1 |
| х2 – 2ху + у2 | | 2 |
| х3 – у3 | | 3 |
| (х + у)( х2 – ху + у2) | | 4 |
| у2 – х2 | | 5 |
| х2 – 4ху + 4у2 | | 6 |
| (х – у)(х + у) | | 7 |
| (х + у)(х2 + 2ху + у2) | | 8 |
| – (х – у) | | 9 |
| (х + у)2 |
| | 1 | | х2 – у2 | | 2 |
| х2 + 2ху + у2 | | 3 |
| у – х | | 4 |
| (х – у)2 | | 5 |
| (х – у)(х2 + ху + у2) | | 6 |
| (х + у)3 | | 7 |
| х3 + у3 | | 8 |
| (х – 2у)2 | | 9 |
| (у – х)(у + х) |
|
|
|
|
| + |
|
|
| 64 | Провести классификацию данных многочленов по способу разложения на множители и заполнить таблицу: 20х3у2 + 4 х2у a4 – b8 2bx – 3ay – 6by + ax b(a + 5) – c(a +5) 27b3 + a6 a2 + ab – 5a – 5b 15a3b + 3a2b3 x2 + 6x + 9 2an – 5bm – 10bn + am 2y(x –5) + x(x – 5) 49m4 – 25n2 3a2 + 3ab – 7a – 7b | Вынесение общего множителя за скобки | Формулы сокращенного умножения | Способ группировки | |
|
|
|
|
|
|
| + |
|
|
| 65 | Заполните пропуски: 1.Произведение разности двух чисел и их суммы равно ___________________этих чисел. 2. (у – 2х) (у + 2х) = _____________________ 3. Формулы сокращенного умножения применяются для упрощения вычислений. Упростить: 73 ∙ 67 = (____+____)(____–____) =_____________=__________ 4. В виде многочлена квадрат данного двучлена записывается так: (а – 3с)2 = ___________________ 5. Используя формулу сокращенного умножения получаем: 522 = (_____+_____)2 = ____________ = _______
|
|
|
|
| + |
| 5 |
| Коммуникативные | У | От | Об | Д | Д/З |
|
| 66 | Заполните пропуски такими одночленами, чтобы выполнялось равенство. Объясните свой выбор. 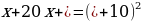
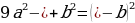
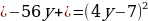
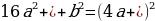
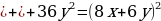
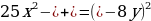 |
| + |
|
|
|
|
| 67 | Найдите ошибки, объясните причину их появления.
1. (4у – 3х)(4у + 3х) = 8у² – 9у²
2. 100х² – 4у² = (50х – 2у)(50х + 2у)
3. (3х + у)² = 9х² – 6ху + у²
4. (6a – 9c)² = 36a² – 54ac + 81c²
5. х³+8 = (х + 2)(х² – 4х + 4) | + |
|
|
|
|
|
| 68 | Заполните пропуски: … – выражение, являющееся произведением чисел, переменных и их степеней, а также числа, переменные и их степени. Стандартный вид одночлена – … числового множителя, стоящего на … и степеней различных переменных. Коэффициент одночлена – числовой … одночлена, записанного в … виде. Многочлен – алгебраическая … одночленов. Стандартный вид многочлена – … , в котором все одночлены записаны в … виде и нет … слагаемых. Подобные слагаемые (члены) – слагаемые, у которых одинаковая … часть. Приведение подобных слагаемых – преобразование, основанное на … свойстве умножения. |
| + |
|
|
|
|
| 69 | Рассмотрите решения заданий на разложение многочлена на множители и расскажите, какие приемы использовались при этом. Пример 1. 36а6в3 – 96а4в4 + 64 а2в5. Решение. 36а6в3 – 96а4в4 + 64 а2в5 = 4а2в3(9а4 – 24а2в + 16в2) = 4а2в3(3а2 – 4в)2 Пример 2. а2 + 2ав + в2 – с2. Решение. а2 + 2ав + в2 – с2 = (а2 + 2ав + в2) – с2 = (а +в)2 – с2 = (а + в – с)(а +в +с). Пример 3. у3 – 3у2 + 6у – 8. Решение. у3 – 3у2 + 6у – 8 = (у3 – 8) – (3у2 – 6у) = (у – 2)(у2 + 2у + 4) – 3у(у – 2) = (у – 2)(у2 – у + 4). |
|
| + |
|
|
|
| 70 | Является ли 292 – 132 простым числом? Ответ объясните. |
|
|
|
| + |
| 5 |
| Регулятивные | У | От | Об | Д | Д/З |
|
| 71 | Запишите решение, исправив ошибки: 1) х2 – 49 = (х – 7) (х – 7).
2) 4 х2 – 1 = (4 х – 1) (4х + 1).
3) 25 – 9 х2 = (5 – 3х) + (5 + 3х).
4) 81 + х2 = (9 + х) (9 – х). |
|
|
| + |
|
|
| 72 | Вычислить наиболее рациональным способом: 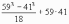 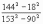 |
|
|
|
| + |
|
| 73 | Соединить линиями многочлены с соответствующими им способами разложения на множители.  |
| + |
|
|
|
|
| 74 | Выберите рисунок, иллюстрирующий тождество (а + в)(а – в) = а2 – в2 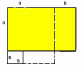 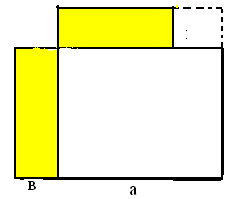 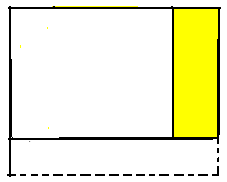
|
|
|
|
| + |
|
| 75 | Преобразуйте, где возможно, выражение в разность квадратов. | 1) х – у(х + у); | 7) (х + у)(х + у); | | 2) (в – а)в + а; | 8) а2 +2(2 – а2); | | 3) (х – у)(х + у); | 9) (а2 + 2)(2 + а2); | | 4) ху + (х + у); | 10) (а2 + а)(а2 – 2); | | 5) (х + у)(х – 1); | 11) (2 – а2)(а2 – 2); | | 6) (х + у)(х + у + 1); | 12) (а2 + 2)(2 – а2). |
|
| + |
|
|
|
Тема 6. Преобразование целых выражений. Разложение многочлена на множители.
| 6 |
| Познавательные УУД | У | От | Об | Д | Д/З |
|
| 76 | Найдите целые выражения среди выражений: 3х +7у; 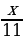 ; ; 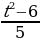 ; 10х + (2х – 3у)(х – у); ; 10х + (2х – 3у)(х – у); 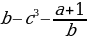 ; ; 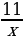 ; ; 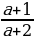 ; ; 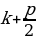 ; а3. ; а3. | + |
|
|
|
|
|
| 77 | Сформулируйте задание для каждого выражения и выполните его: 1) (2а – в)(2а + в) + (в – с)(в + с) + (с – 2а)(с + 2а). 2) х2(х – 4) – (х – 4). 3) (3а + 7b)2 – (9а – 5b)2. 4) (692 – 31 ∙ 31) : 19. 5) а(а – 2) – 5а + 10. 6) 5 а2 + 10аb + 5b2. 7) у 4 – 8 у 2 +16 . 8) (а – 8)(а + 4) – 2а(5 – а). 9) (а – х)2 – (а + х)2 10) (а+(в + с))2 |
| + |
|
|
|
|
| 78 | Среди данных выражений, найдите равные пары: (2х – у)2;
2(2х – у) 2;
4(2х – у) 2;
(4х – 2у) 2;
0,5(4х – 2у) 2. |
|
| + |
|
|
|
| 79 | Какие из следующих многочленов квадраты? а2 + 4а + 4;
а2 + 12а + 9;
х4 + 6 х2 у2 + 9 у2;
а2 – 10 а в2 + 25в4;
4 а х2 – 6а + 16;
х2 + 18х2 + 9. |
|
|
|
| + |
|
| 80 | Вычислите: 1. (2 – 1)(2 + 1)(22 + 1) (24 + 1) (28 + 1) (216 + 1) – 232. 2. (1 – 3)(3 + 1)(32 + 1) (34 + 1) (38 + 1) (316 + 1) + 332. |
|
| + |
|
|
| 6 |
| Коммуникативные | У | От | Об | Д | Д/З |
|
| 81 | Продолжите предложение. Разложить многочлен на множители это значит... Способы разложения многочлена на множители: Метод разложения на множители используется: |
| + |
|
|
|
|
| 82 | Объясните каждый шаг решения уравнения: 1) x3 – 4x = 0 x(x2 – 4)= 0 x(x – 2)(x + 2) = 0 x = 0 или x – 2 = 0 или x + 2 = 0 x = 2 x = –2 Ответ: 0; 2; –2.
2) x3 – 2x2 – x + 2 = 0 x2(x – 2) – (x – 2) = 0 (x – 2)(x2 – 1) = 0 (x – 2)(x + 1)(x – 1) = 0 x – 2 = 0 или x + 1 = 0 или x – 1 = 0 x =2 x = –1 x = 1 Ответ: 2; –1; 1. |
| + |
|
|
|
|
| 83 | Решите уравнения и объясните каждый шаг решения уравнения: а) 49x2 – 42x + 9 = 0; б) x2+ 6x – 7 = 0; в) x4+ 4y4 = 0 |
|
|
|
| + |
|
| 84 | Найдите значения числовых выражений, объяснив, какой способ разложения на множители использовали: 45 · 93 + 45 · 7 = 712 + 2 · 71 · 29 + 292 = 25 · 59 + 25 · 41 + 52 · 13 – 52 · 12 = 599 · 601 = |
| + |
|
|
|
|
| 85 | Составьте вопросы для зачета по теме «Преобразование целого выражения в многочлен. Разложение многочлена на множители.» |
|
|
|
| + |
| 6 |
| Регулятивные | У | От | Об | Д | Д/З |
|
| 86 | Ответьте на вопросы: Можно ли разложить по формуле сокращенного умножения трехчлен х² – 4х + 1? Верно ли, что х² + у² = (х + у)(х – у)? Верно ли, что (х – у) = у – х? Верно ли, что (4 – х)² = (х – 4)²? Верно ли, что 49х² – 28х +16 = (7х – 4)²? Верно ли, что 1 – 9х³ = (1 – 3х)(1 + 3х)? Верно ли, что 5a – 5b + ха – хb = (5 + х)(а – b)? |
| + |
|
|
|
|
| 87 | Найдите ошибку и исправьте ее: 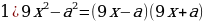 ; ; 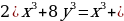 3) 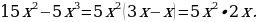 |
|
|
|
| + |
|
| 88 | Рассмотрите два способа разложения на множители двучлена х4 – х2: х2 – х4 = (х – х2) (х + х2) = х (1 – х) ·х (1 + х) = х2 (1 – х) (1 + х);
х2 – х4 = х2 (1 – х2) = х2(1 – х)(1 + х). Какой из способов вам больше нравится и почему? |
|
| + |
|
|
|
| 89 | Изучите задания на сравнение значения выражения с нулём: 1) x2 + 10 и 0. Т.к. x2 ≥ 0, 10 0, значит x2 + 10 0 . 2) –2x2 – 5 и 0. Т.к. –2x2 ≤ 0, –5 x2 – 5 3) x2 – 16x + 64 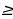 0. 0. Т.к. (x – 8)2 ≥ 0, значит x2 – 16x + 64 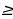 0. 0. 4) –x2 – 4x – 4 и 0, –(x2 + 4x + 4) и 0. Т.к. –(x + 2)2 ≤ 0, значит –x2 – 4x – 4 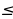 0. 0. Сравните: а) –x2 – 1 и 0, б) 7x2 + 9 и 0, в) x2 + 6x +10 и 0. |
|
|
|
| + |
|
| 90 | Изучите ещё один способ разложения многочлена на множители.
Разложите на множители 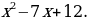 1) Дан многочлен стандартного вида. 2) Степень данного многочлена вторая. 3) Выполним умножение: 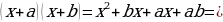 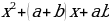 . . Таким образом, 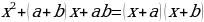 . . Проведем аналогию с данным многочленом: a + b = –7; ab = 12. Попробуем подобрать такие числа, чтобы при сложении они давали –7, а при умножении 12. В нашем случае это числа – 3 и – 4. Тогда наш многочлен разложится на множители: 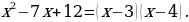
Разложите этим способом многочлен на множители: 1) 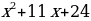 ; 2) ; 2) 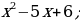 3) 3) 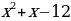 . . |
|
| + |
|
|
Тема 7. Системы линейных уравнений.
| 7 |
| Познавательные УУД | У | От | Об | Д | Д/З |
|
| 91 | Изучите решение заданий на выражение одной переменной через другую:
| 1) 2х + у = 5, у = 5 – 2х. | 2) 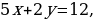 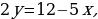 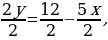
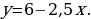
| 3) 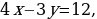 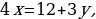 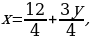
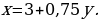 |
Составьте алгоритм и выполните задание: 3х + 2у = 6 а) выразите х через у, б) выразите у через х.
|
| + |
|
|
|
|
| 92 | | В уравнениях выразите у через х | у = у = | | Графиками уравнений являются прямые. В одной и той же координатной плоскости постройте графики уравнений. | 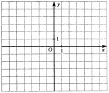
| | Найдите координаты точки пересечения графиков. | х = у = | | Запишите ответ. | (__; __) | Решите систему уравнений 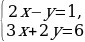 графически по плану: графически по плану:
|
|
|
|
| + |
|
| 93 | Опишите равенством зависимость между переменными х и у, если: 1) сумма чисел х и у равна 43; 2) среднее арифметическое чисел х и у равно 24; 3) туристы преодолели 24 км и шли 3 ч со скоростью х км/ч и 2 ч со скоростью у км/ч; 4) у девочки х пятирублевых монет и у двухрублевых монет на общую сумму 36 руб.; 5) около причала находилось х двухместных и у трехместных лодок; всего в эти лодки может поместиться 14 человек; 6) Лене х лет, а её брату у лет. 4 года назад Лена была в 2 раза старше своего брата; 7) периметр прямоугольника со сторонами хсм и у см равен 72 см. | + |
|
|
|
|
|
| 94 | а) Является ли решением системы пара чисел? Покажите стрелкой. | 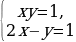
| (1; 1) 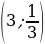
| б) Выясните, имеет ли решение система, если да, то сколько? Покажите стрелкой. | 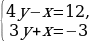
| а) одно решение, б) бесконечно много решений, в) решений нет |
| + |
|
|
|
|
|
| 95 | Составьте алгоритм решения системы двух линейных уравнений с двумя переменными нужным способом с помощью карточек. Способом подстановки: Способом сложения: Выразим из какого-нибудь уравнения одну из переменных через другую. Подставим найденное значение переменной в одно из уравнений исходной системы, найдем вторую переменную. Сложить или вычесть полученные уравнения. Найденное выражение подставляем во второе уравнение. Решаем полученное уравнение с одной переменной. Найдем соответствующее значение второй переменной. Необходимо уравнять модули коэффициентов при одном из неизвестных. Записать ответ. Решить полученное уравнение с одной переменной и найти значение этой переменной. Записать ответ.
| + |
|
|
|
|
| 7 |
| Коммуникативные | У | От | Об | Д | Д/З |
|
| 96 | 1) Вася решал задачу, которая начинается словами: «В прямоугольнике одна сторона…» Он составил систему уравнений: 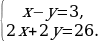 Сформулируйте задачу, которую решал Вася. |
| + |
|
|
|
|
| 97 | Ответьте на вопросы: 1. Дайте определение линейного уравнения с двумя переменными; 2. Что называют решением уравнения с двумя переменными? 3.Что является графиком уравнения ax + by = c, где х, y –переменные, 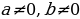 . . 4. Если говорят, что задана система уравнений, что это значит? 5. Что является решением системы линейного уравнения с двумя переменными? 6. Что, значит, решить систему линейного уравнения с двумя переменными? 7. Сколько решений может иметь система линейного уравнения с двумя переменными? Составьте ещё вопросы по этой теме. |
|
|
|
| + |
|
| 98 | Определите рациональный способ решения и обоснуйте свой выбор. 1) 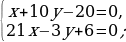 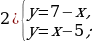 3) 3) 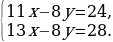 |
|
| + |
|
|
|
| 99 | Расскажите, как решают систему двух линейных уравнений с двумя переменными способом подстановки; способом сложения. | + |
|
|
|
|
|
| 100 | Продолжите заполнение диагностической карты для определения своих знаний и умений по теме «Системы линейных уравнений» (можно использовать учебник)
| ЗНАЮ | УМЕЮ | | Линейные уравнения с двумя переменными | | Определение линейного уравнения с двумя переменными | Приводить примеры линейного уравнения с двумя переменными | |
| | |
| | |
| | | Решение систем линейных уравнений | |
| | |
| |
|
|
|
|
| + |
| 7 |
| Регулятивные | У | От | Об | Д | Д/З |
|
| 101 | Задача из “Всеобщей арифметики” Ньютона. Лошадь и мул шли бок о бок с тяжелой поклажей на спине. Лошадь жаловалась на свою непомерно тяжелую ношу. “Чего же ты жалуешься? – отвечал ей мул. – Ведь если я возьму у тебя один мешок, ноша моя станет вдвое тяжелее твоей. А вот если бы ты сняла с моей спины один мешок, то твоя поклажа стала бы одинакова с моей. Сколько мешков несла лошадь и сколько мул? Заполните ячейки таблицы: | Родной язык | Язык алгебры | | Поклажа лошади | х | | Поклажа мула | у | | Если я возьму у тебя один мешок |
| | Ноша моя |
| | А вот если ты снимешь с моей спины один мешок |
| | Твоя поклажа |
| Зная, что ноша моя станет тяжелее твоей, составьте первое уравнение системы _________________________________ . Зная, что твоя поклажа стала бы одинакова с моей, составьте второе уравнение _____________________________.
|
| + |
|
|
|
|
| 102 | 1) 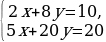 Убедитесь в том, что графическая модель системы – это совпадающие прямые. Сравните отношение коэффициентов при x, при y и свободных членах в системе. Сформулируйте признак, по которому можно определить, что система имеет бесконечно много решений. 2) 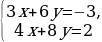 Убедитесь в том, что графическая модель системы – это параллельные прямые. Сравните отношение коэффициентов при x, при y и свободных членах в системе. Сформулируйте признак, по которому можно определить, что система не имеет решений. 3) 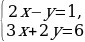 Убедитесь в том, что графическая модель системы – это пересекающиеся прямые. Сравните отношение коэффициентов при x, при y и свободных членах в системе. Сформулируйте признак, по которому можно определить, что система имеет единственное решение. |
| + |
|
|
|
|
| 103 | Сделайте вывод о количестве решений системы уравнений, установите связь между угловыми коэффициентами и свободными членами: 1) 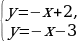 k1 ⎕k2, b1 ⎕b2, решений __________; 2) 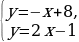 k1 ⎕k2, решений __________; 3) 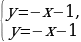 k1 ⎕k2, b1 ⎕b2, решений __________; Сделайте выводы и заполните пропуски: Если угловые коэффициенты прямых, являющихся графиками этих функций, различны, то эти прямые ______________ и система имеет ___________решение. Если угловые коэффициенты прямых одинаковы, а точки пересечения с осью у различны, то прямые ________, а система __________________________. Если угловые коэффициенты и точки пересечения с осью у одинаковы, то прямые ___________ и система ___________________________________________. | + |
|
|
|
|
|
| 104 | Заполните таблицу: |
| Связь между коэффициентами | | y=k1x+b1 y=k2x+b2 | a1x+b1y=c1 a2x+b2y=c2 | | Нет решений |
|
| | Много решений |
|
| | Единственное решение |
|
|
|
|
|
| + |
|
|
| 105 | При каких значениях параметра b система уравнений 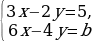
а) имеет бесконечное множество решений; б) не имеет решений. |
|
| + |
|
|






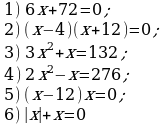
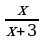
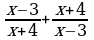
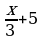
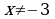
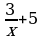
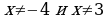
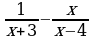
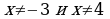
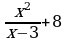
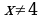
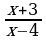
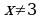
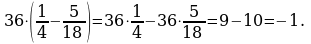
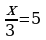
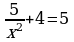
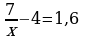
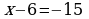
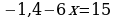
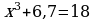
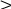
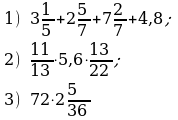
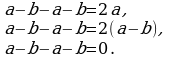










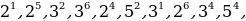
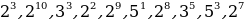
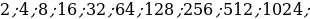
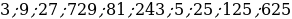
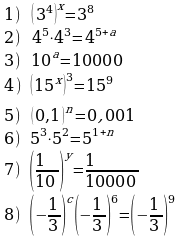
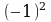 сключи лишнее, объясни своё решение.
сключи лишнее, объясни своё решение.
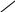
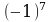

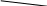
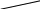
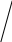
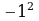
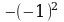 -1
-1 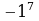
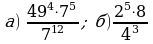
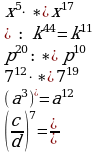
 Представьте 64 в виде степени с основанием 2; -2; -8. Куб какого числа равен 64? Существует ли еще какой-нибудь способ представления 64 в виде степени с натуральным показателем? Если да, то назовите его.
Представьте 64 в виде степени с основанием 2; -2; -8. Куб какого числа равен 64? Существует ли еще какой-нибудь способ представления 64 в виде степени с натуральным показателем? Если да, то назовите его. 

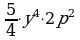
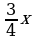

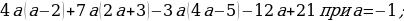
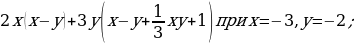
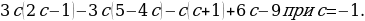
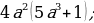
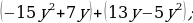
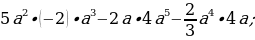
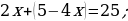
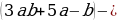
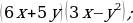
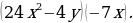

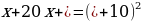
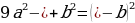
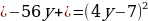
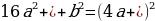
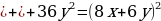
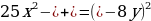
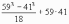
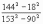




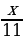 ;
; 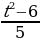 ; 10х + (2х – 3у)(х – у);
; 10х + (2х – 3у)(х – у); 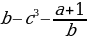 ;
; 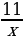 ;
; 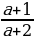 ;
; 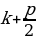 ; а3.
; а3. 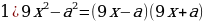 ;
;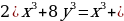
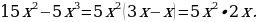
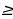 0.
0.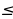 0.
0. 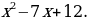
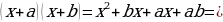
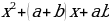 .
.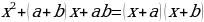 .
.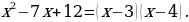
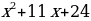 ; 2)
; 2) 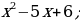 3)
3) 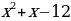 .
.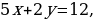
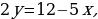
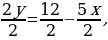
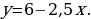
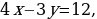
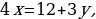
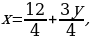
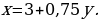

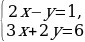 графически по плану:
графически по плану: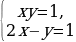
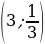
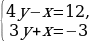
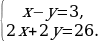
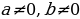 .
.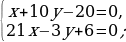
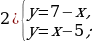 3)
3)