КИМ Основы тригонометрии

Министерство образования и науки Хабаровского края

Краевое государственное бюджетное образовательное учреждение

среднего профессионального образования

«Комсомольский-на-Амуре строительный колледж»

_____________________________________________________________________________

Контрольно-измерительный материал для текущего контроля знаний

по __Математике____ общеобразовательного цикла

наименование дисциплины или темы ПМ

в рамках основной профессиональной образовательной программы

по специальности

230115 Программирование в компьютерных системах

код, название

2013 год

Контрольно-измерительный материал охватывает разделы рабочей программы «_Основы тригонометрии_» (_40_часов), что составляет 13,8%.

Контрольно-измерительный материал состоит из 3 частей.

Часть 1 включает 27 заданий (А1-А27) 1 и 2 уровней освоения учебного материала. К каждому из них даны 4 варианта ответа, из которых только один правильный.

Часть 2 состоит из 8 заданий (В1-В8) 2 уровня освоения учебного материала. Ответы к этим заданиям должны быть сформулированы самостоятельно.

Часть 3 состоит из одного задания (С1) 3 уровня освоения учебного материала и представляет собой письменную работу.

Время выполнения - _80_мин. из расчета 1,5 мин. на задания части 1,2 и 30 мин. – на часть 3.

Правильный ответ в зависимости от сложности каждого задания оценивается одним или несколькими баллами. Баллы, полученные при выполнении задания, суммируются.

Разработчик: Бажутова Т.А., преподаватель Математики

Ф.и.о.

КГБОУ СПО КСК

Рассмотрено и утверждено на заседании ПЦК ______________________________

название

Протокол ____ от «______» ________20____г.

Председатель ПЦК __________________/и.о. фамилия/

Вариант 1

Часть 1

При выполнении заданий этой части обведите номер, выбранного ответа.

А1 Определите знак выражения :

1

2 =0

3 0

4 =1

А2 Вычислите :

1

2

3

4 0

А3 Найдите значение выражения :

1 0

2 2

3 1/2

4 1

А4 Вычислите :

1

2 1

3 4

4 0

А5 Вычислите :

1 1

2 1/2

3 -1

4 0

А6 Вычислите :

1 1/2

2 0

3 1

4

А7 Упростите :

1 -1

2 1/2

3 1

4 0

А8 Вычислите :

1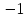

2

3

4

А9 Найдите значение :

1

2 1

3

4 0

А10 Могут ли одновременно быть справедливы равенства и :

1

2

А11 Найдите значение cos α, если и :

1

2

3 1/2

4 0,6

А12 Могут ли одновременно быть справедливы равенства и :

1

2

А13 Упростите :

1

2

3

4

А14 Найдите значение cos α, если и - угол 4 четверти:

1

2

3

4 0

А15 Упростите выражение :

1

2

3

4

А16 Найти градусную меру угла :

1

2 ⁰

3 ⁰

4 120⁰

А17 Решите :

1

2

3

4 1

А18 Решите :

1

2

3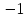

4 1/2

А19 Вычислите :

1

2

3

4 1/2

А20 Вычислить :

1

2

3

4 0

А21 Определите знак выражения :

1 0

2 =0

3

4 =1

А22 Определите знак выражения :

1 0

2 =0

3 =0

4

А23 Вычислите :

1

2

3

4 1/2

А24 Вычислите :

1

2

3

4 ½

А25 Упростить :

1 1/2

2

3 1/8

4

А26 Упростить :

1

2

3

4

А27 Упростить :

1

2

3

4

Часть 2

При выполнении заданий этой части ответы записываются словами.

В1 Вычислите:

________________________________________________________________

место для ответа

В2 Вычислите

________________________________________________________________

место для ответа

В3 Найдите значение выражения

________________________________________________________________

место для ответа

В4 Упростите выражение и найдите его значение, если

________________________________________________________________

место для ответа

В5 Упростите выражение и найдите его значение, если

________________________________________________________________

место для ответа

В6 Найдите значение выражения , если , α и β – углы второй четверти

________________________________________________________________

место для ответа

В7 Найдите значение выражения

________________________________________________________________

место для ответа

В8 Дано . Найдите

________________________________________________________________

место для ответа

Часть 3

Запишите сначала номер задания С1, а затем приступите к его выполнению.

С1 Упростите выражение и найдите его значение, если .

Вариант 2

Часть 1

При выполнении заданий этой части обведите номер, выбранного ответа.

А1 Определите знак выражения :

1

2 =0

3 0

4 =1

А2 Вычислите :

1

2

3

4 0

А3 Найдите значение выражения :

1 0

2 1

3 1/2

4 2

А4 Вычислите :

1

2 1

3

4 0

А5 Вычислите :

1 1

2 1/2

3 -1

4 0

А6 Вычислите :

1 1/2

2 0

3 1

4

А7 Упростите :

1

2 0

3 tg

4

А8 Вычислите :

1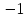

2

3

4

А9 Найдите значение :

1

2

3

4

А10 Могут ли одновременно быть справедливы равенства и :

1

2

А11 Найдите значение tg α, если и :

1

2

3 1/2

4 0,6

А12 Могут ли одновременно быть справедливы равенства и :

1

2

А13 Упростите :

1

2

3

4

А14 Найдите значение sin α, если и - угол 4 четверти:

1

2

3

4

А15 Вычислите , если :

1

2

3

4

А16 Найти градусную меру угла :

1

2 ⁰

3 ⁰

4

А17 Решите :

1

2

3

4 1

А18 Решите :

1

2

3

4

А19 Вычислите :

1

2

3

4 1/2

А20 Вычислить :

1

2

3

4 0

А21 Определите знак выражения :

1 0

2 =0

3

4 =1

А22 Определите знак выражения :

1 =1

2 =0

3

4 0

А23 Вычислите :

1

2

3

4 1/2

А24 Вычислите :

1

2

3

4 0

А25 Упростить :

1

2

3 1/8

4

А26 Упростить :

1

2

3

4

А27 Упростить :

1

2

3

4

Часть 2

При выполнении заданий этой части ответы записываются словами.

В1 Вычислите:

________________________________________________________________

место для ответа

В2 Вычислите

________________________________________________________________

место для ответа

В3 Найдите значение выражения

________________________________________________________________

место для ответа

В4 Упростите выражение и найдите его значение, если

________________________________________________________________

место для ответа

В5 Упростите выражение и найдите его значение, если

________________________________________________________________

место для ответа

В6 Найдите значение выражения , если , α и β – углы первой четверти

________________________________________________________________

место для ответа

В7 Найдите значение выражения

________________________________________________________________

место для ответа

В8 Найти sin 2α, если и

________________________________________________________________

место для ответа

Часть 3

Запишите сначала номер задания С1, а затем приступите к его выполнению.

С1 Вычислить значение выражения если .

Спецификация

контрольно-измерительных материалов

Объектами проверки выступают элементы содержания, а также умения, способы познавательной деятельности, определенные требованиями ФГОС СПО.

для достижения поставленной цели разработан и используется комплекс заданий, различающихся по характеру, направленности, уровню сложности.

Структура и содержание контрольно-измерительных материалов.

Части работы	Число заданий	Максимальный балл	Процент максимального балла за задания данного вида от максимального балла за всю работу
Часть 1	27	27	54
Часть 2	8	16	32
Часть 3	1	7	14
Итого	36	50	100

Вариант №1

Задание	Ответ	Проверяемые элементы	Уровень сложности заданий	Максимальный балл за выполнение заданий
А1	3	Понятие синуса, косинуса, тангенса и котангенса числового аргумента	базовый	1
А2	1	Синус суммы и разности	базовый	1
А3	4	Синус суммы и разности	базовый	1
А4	1	Косинус суммы и разности	базовый	1
А5	2	Синус двойного аргумента	базовый	1
А6	4	Косинус двойного аргумента	базовый	1
А7	3	Косинус двойного аргумента	базовый	1
А8	3	Тангенс двойного аргумента	базовый	1
А9	1	Формулы приведения	базовый	1
А10	2	Соотношения между тригонометрическими функциями одного аргумента	базовый	1
А11	2	Основное тригонометрическое тождество	базовый	1
А12	1	Произведение тангенса и котангенса одного и того же аргумента	базовый	1
А13	4	Произведение тангенса и котангенса одного и того же аргумента	базовый	1
А14	3	Зависимость между котангенсом и синусом одного и того же аргумента	базовый	1
А15	2	Косинус суммы и разности	базовый	1
А16	4	Формулы перехода от градусной меры к радианной и обратно	базовый	1
А17	2	Четность и нечетность тригонометрических функций	базовый	1
А18	3	Четность и нечетность тригонометрических функций	базовый	1
А19	1	Периодичность тригонометрических функций	базовый	1
А20	1	Преобразования тригонометрических выражений	базовый	1
А21	3	Тригонометрические операции	базовый	1
А22	4	Тригонометрические операции	базовый	1
А23	2	Тригонометрические операции	базовый	1
А24	1	Тригонометрические операции	базовый	1
А25	2	Тригонометрические операции	базовый	1
А26	3	Тригонометрические операции	базовый	1
А27	4	Тригонометрические операции	базовый	1
В1		Понятие синуса, косинуса, тангенса и котангенса числового аргумента	повышенный	2
В2	1	Тангенс суммы и разности	повышенный	2
В3	0,5	Тригонометрия	повышенный	2
B4	1	Тригонометрия	повышенный	2
В5	0	Тригонометрия	повышенный	2
В6	13/85	Тригонометрия	повышенный	2
B7	0	Тригонометрия	повышенный	2
В8	4,2	Тригонометрия	повышенный	2
С1	1	Тригонометрия	сложный	7

Вариант №2

Задание	Ответ	Проверяемые элементы	Уровень сложности заданий	Максимальный балл за выполнение заданий
А1	1	Понятие синуса, косинуса, тангенса и котангенса числового аргумента	базовый	1
А2	3	Синус суммы и разности	базовый	1
А3	2	Синус суммы и разности	базовый	1
А4	1	Косинус суммы и разности	базовый	1
А5	2	Синус двойного аргумента	базовый	1
А6	4	Косинус двойного аргумента	базовый	1
А7	3	Косинус двойного аргумента	базовый	1
А8	3	Тангенс двойного аргумента	базовый	1
А9	4	Формулы приведения	базовый	1
А10	1	Соотношения между тригонометрическими функциями одного аргумента	базовый	1
А11	1	Основное тригонометрическое тождество	базовый	1
А12	2	Произведение тангенса и котангенса одного и того же аргумента	базовый	1
А13	1	Зависимость между тангенсом и косинусом одного и того же аргумента	базовый	1
А14	4	Зависимость между котангенсом и синусом одного и того же аргумента	базовый	1
А15	3	Синус двойного аргумента	базовый	1
А16	2	Формулы перехода от градусной меры к радианной и обратно	базовый	1
А17	1	Четность и нечетность тригонометрических функций	базовый	1
А18	4	Четность и нечетность тригонометрических функций	базовый	1
А19	2	Периодичность тригонометрических функций	базовый	1
А20	3	Преобразования тригонометрических выражений	базовый	1
А21	1	Тригонометрические операции	базовый	1
А22	4	Тригонометрические операции	базовый	1
А23	3	Тригонометрические операции	базовый	1
А24	2	Тригонометрические операции	базовый	1
А25	1	Тригонометрические операции	базовый	1
А26	4	Тригонометрические операции	базовый	1
А27	4	Тригонометрические операции	базовый	1
В1		Понятие синуса, косинуса, тангенса и котангенса числового аргумента	повышенный	2
В2	1	Тангенс суммы и разности	повышенный	2
В3	0	Тригонометрия	повышенный	2
B4	0,6	Тригонометрия	повышенный	2
В5	10	Тригонометрия	повышенный	2
В6	77/85	Тригонометрия	повышенный	2
B7	0	Тригонометрия	повышенный	2
В8	615	Тригонометрия	повышенный	2
С1	8	Тригонометрия	сложный	7

Статистика