| МИНИСТЕРСТВО ПРОСВЕЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский государственный Гуманитарно-педагогический университет»
Математический факультет Кафедра высшей математики и методики обучения математике |
|
|
|
|
| Курсовая работа по дисциплине (модулю) «Математический анализ»
|
| Виды комбинаторных задач и методы их решения |
|
|
| Работу выполнил: обучающаяся 121 группы направления подготовки 44.03.05 Педагогическое образование (с двумя профилями подготовки), направленность (профиль) «Математика и Информатика» Гурина Анна Олеговна ________________ (подпись) |
| «Допущена к защите» Заведующий кафедрой ________________ (подпись) «___»___________20__г. |
| Руководитель: канд. педагогических наук, доцент кафедры высшей математики и методики обучения математике Черемных Елена Леонидовна ________________ (подпись) |
| Оценка: _________________ Руководитель: ___________ (подпись) |
|
|
|
|
Пермь 2020 |
|
оглавление
введение 3
глава 1. комбинаторика как наука 5
1.1. Понятие комбинаторики 5
1.2. История комбинаторики 8
1.3. Классические комбинаторные задачи 11
1.4. Разделы комбинаторики 14
глава 2. решение основных видов комбинаторных задач 16
2.1. Комбинаторные правила суммы и произведения 16
2.1. Перестановки, сочетания и размещения без повторений 18
2.2. Перестановки, сочетания и размещения с повторениями 21
2.3. Комплекс задач на применение формул комбинаторики 24
заключение 28
список литературы 30
введение
Исследование посвящено видам комбинаторных задач и методам их решения. Актуальность темы обусловлена тем, что комбинаторика успешно применяется в различных областях науки: в генетике, информатике, статистической физике, в линейном программировании, статистике и т.д.
Комбинаторика возникла еще в древние времена и развивается по сей день. Она связана с такими областями математики, как алгебра, геометрия и теория вероятности. Её практическое значение даже в жизни обычного человека сложно переоценить. Мы часто решаем комбинаторные задачи, сами о том не подозревая. Например, рассаживая гостей на мероприятии, составляя график дежурств и т.д.
Целью исследования является изучение методов решения основных видов комбинаторных задач и составление комплекса задач на применение формул комбинаторики.
Для достижения поставленной цели были сформулированы следующие задачи исследования:
анализ исторической и математической литературы по теме исследования;
выявление основных видов комбинаторных задач и методов их решения;
подбор примеров на каждый вид и метод решения комбинаторных задач.
составление комплекса заданий по комбинаторике, охватывающего все рассмотренные виды комбинаторных задач и методы их решения.
Объектом исследования являются задачи комбинаторики.
Предметом исследования являются методы решения основных видов комбинаторных задач.
Работа состоит из введения, основной части, содержащей две главы, заключения и списка литературы, включающего в себя 15 наименований.
Во введении представлены актуальность темы курсовой работы, цели и задачи исследования, краткая характеристика структуры работы и описание её частей.
В первой главе рассмотрены понятие комбинаторики, история комбинаторики, основные разделы комбинаторики, а также классические комбинаторные задачи.
Во второй главе выделены основные виды комбинаторных задач и методы их решения, для каждого вида приведены примеры с подробным решением, составлен комплекс комбинаторных задач на все рассмотренные в работе виды.
В заключении подтверждена актуальность выбранной темы, указаны результаты проведённого исследования, а также рассмотрены возможные варианты дальнейших исследований в рамках данной темы.
глава 1. комбинаторика как наука
Понятие комбинаторики
Согласно источнику «Статистика. Вероятность. Комбинаторика» Я. С. Бродского, комбинаторика или комбинаторный анализ — это раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка) [14, с.19-20].
Также, под комбинаторикой понимают более обширный раздел дискретной математики, включающий, в частности, теорию графов.
Комбинаторика изучает вопрос о том, сколько различных конфигураций, удовлетворяющих тем или иным условиям, можно составить из заданных объектов.
Как указывает источник «Комбинаторика в жизнедеятельности человека и решение комбинаторных задач» И. И. Рогановой, комбинаторика — это важный раздел математики, знание которого необходимо представителям самых разных специальностей. С этими задачами приходится иметь дело физикам, химикам, биологам, лингвистам, экономистам, агрономам, специалистам по кодам, компьютерам, информационным технологиям и т. д.
Начальнику цеха необходимо распределять несколько видов работ между имеющими станками, агроному – разметить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, химику – рассмотреть возможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д.
Комбинаторные методы лежат в основе решения многих задач теории вероятностей, математической статистики и их приложений.
Их используют также для решения транспортных задач (в частности задач по составлению расписаний), для составления планов производства и реализации продукции, в теории случайных процессов, статистике, вычислительной математике, планировании экспериментов, шахматных программах для ЭВМ. [6, с.23].
Согласно данным источника «Конкретная математика. Основание информатики» под редакцией Р. Грэхема, Д. Кнута и О. Паташника, правила комбинаторики также используются для составления и декодирования шифров и для решения других проблем информации. Значительную роль комбинаторные методы играют и в чисто математических вопросах – при изучении конечных геометрий, теории групп и их представлений, неассоциативных алгебр и т.д. [7, с.696-700]
По данным источника «Теоремы и задачи комбинаторной геометрии» В. Г. Болтянского и И. Ц. Гохберга, комбинаторика присутствует в программах учебных заведений различного уровня подготовки. Задачи на комбинаторику и теорию вероятностей можно найти как в учебниках младшей школы, так и средней, и старшей. Данные задачи используются в том числе и при составлении заданий Единого Государственного Экзамена. Даже в высших учебных заведениях присутствуют дисциплины, которые предусматривают изучение вопросов комбинаторики и теории вероятностей.
В повседневной жизни нередко возникают проблемы, которые имеют не один, а несколько вариантов решения. Чтобы сделать правильный выбор, очень важно не упустить ни один из них. Для этого надо уметь осуществлять перебор всех возможных вариантов или хотя бы подсчитывать их число. Такого рода задачи называют комбинаторными. [15, с.76-80]
Тематика современной комбинаторики, как гласит источник «Популярная комбинаторика» под редакцией Н.Я. Виленкина, разнообразна: перечислительные и экстремальные задачи, проблемы существования, выбора и расположения, геометрические и алгебраические интерпретации [11, с.44].
Как указывается в источнике «Комбинаторика» Н. Я. Виленкина, А. Н. Виленкина и П. А. Виленкина, в математической литературе отмечаются три отличительные черты комбинаторных задач, которые заключаются в следующем:
все объекты, описываемые в задачах, состоят из отдельных дискретных элементов.
множества этих элементов конечны.
преимущество отдано двум видам операций: отбор подмножеств и упорядочению элементов множества.
Задачи комбинаторики могут включать в себя вопросы существования комбинаторных конфигураций, алгоритмы их построения, оптимизацию таких алгоритмов, а также вопросы определения числа всех возможных конфигураций.
Комбинаторные задачи, с точки зрения теории множеств, — это задачи на определение числа возможных конечных множеств или кортежей с определенными свойствами, которые можно составить из данных элементов.
[5, с.99-102]
История комбинаторики
Начав с анализа головоломок и азартных игр, комбинаторика оказалась исключительно полезной для решения практических задач почти во всех разделах математики. Кроме того, комбинаторные методы оказались полезными в статистике, генетике, лингвистике и многих других науках.
Согласно источнику «С древнейших времен до начала Нового времени» под редакцией А.П. Юшкевича, первые упоминания комбинаторики можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо.
Классическая задача комбинаторики: «сколько есть способов извлечь m элементов из N возможных» упоминается ещё в сутрах древней Индии (начиная примерно с IV века до н. э.). Индийские математики, видимо, первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона.
Античные греки также рассматривали отдельные комбинаторные задачи, хотя систематическое изложение ими этих вопросов, если оно и существовало, до нас не дошло.
Хрисипп (III век до н. э.) и Гиппарх (II век до н. э.) подсчитывали, сколько следствий можно получить из 10 аксиом; методика подсчёта нам неизвестна, но у Хрисиппа получилось более миллиона, а у Гиппарха — более 100000. Какие-то комбинаторные правила пифагорейцы, вероятно, использовали при построении своей теории чисел и нумерологии (совершенные числа, фигурные числа, пифагоровы тройки и др.).
В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями. [13, с.198-204]
В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Герсонид (XIV век). Ибн Эзра подсчитывал число размещений с перестановками в огласовках имени Бога и обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний.
Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, 13 век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.
В Новое время комбинаторика стремительно развивалась, благодаря трудам многих выдающихся учёных. Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей.
В источнике «Математика XVII столетия» под редакцией А. П. Юшкевича сказано, что в историю зарождавшейся теории вероятностей вошла переписка заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.
Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника.
Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». [8, с.299-304]
По словам А. П. Юшкевича в источнике «Математика XVIII столетия», термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713 г.) множество сведений по комбинаторике.
В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653 г., опубликован в 1665 г.). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли. Он же использовал и термин «размещение» (arrangement).
Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера.
Он детально рассмотрел, например, следующие проблемы:
задача о ходе коня;
задача о семи мостах, с которой началась теория графов;
построение греко-латинских квадратов;
обобщённые перестановки.
Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями. [9, с.379-383]
Классические комбинаторные задачи
По указанным в источнике «Развитие некоторых классических комбинаторных задач» А. Е. Малых, А. А. Давыдовой данным, классическими комбинаторными задачи являются следующие задачи:
Магический квадрат (рис. 1) - квадратная таблица (n * n) целых чисел от 1 до n такая, что суммы чисел вдоль любого столбца, любой строки и двух диагоналей таблицы равны одному и тому же числу  . Число n называют порядком магического квадрата. Доказано, что магический квадрат можно построить для любого
. Число n называют порядком магического квадрата. Доказано, что магический квадрат можно построить для любого  .
.
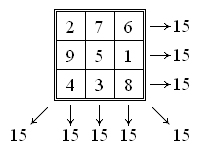
Рис.1. Магический квадрат
Греко-латинский квадрат или эйлеров квадрат (рис. 2) — квадрат N×N в каждой клетке которого стоят 2 числа от 1 до N так, что выполняются условия:
в каждой строке и столбце каждая цифра встречается один раз на первом месте в паре, и один раз на втором.
каждая цифра стоит в паре с каждой другой цифрой и с самой собой по одному разу.
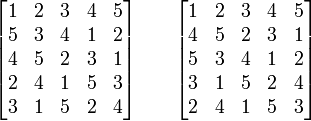
Рис.2. Греко-латинский квадрат
Данную тему рассматривают А. Е. Малых и А. С. Каленкова в источнике «Об исследовании Леонардом Эйлером латинских квадратов». [10, с.102-116]
Задача размещения – одна из классических комбинаторных задач, в которой требуется определить чисто способ размещения m различных предметов в n различных ячейках с заданным числом r пустых ячеек.
Задача коммивояжёра (рис. 3) — одна из самых известных задач комбинаторной оптимизации, заключающаяся в поиске самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город.
В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и тому подобное) и соответствующие матрицы расстояний, стоимости и тому подобного. Как правило, указывается, что маршрут должен проходить через каждый город только один раз.
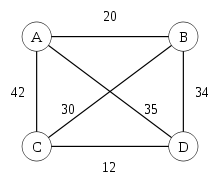
Рис.3. Частный случай задачи коммивояжёра
Бином Ньютона – формула возведения двухчлена (a + b) в целую неотрицательную степень n. Строго говоря, всю формулу нельзя назвать биномом, так как «бином» переводится как «двучлен». Кроме того, формула разложения была известна еще до Ньютона, Исаак Ньютон распространил это разложение на случай n n – дробного. Цель изучения бинома Ньютона – упрощение вычислительных действий.
Знакомая нам из школьного курса математики формула сокращенного умножения «квадрат суммы» - это частный случай бинома Ньютона для n = 2.
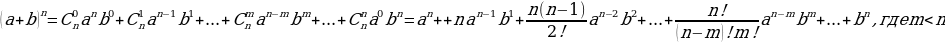
Где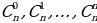 – биномиальные коэффициенты, полученные с использованием операции сложения с помощью треугольника Паскаля.
– биномиальные коэффициенты, полученные с использованием операции сложения с помощью треугольника Паскаля.
Треугольник Паскаля (рис. 4) – это бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси.
Назван в честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают естественным образом в алгебре, комбинаторике, теории вероятностей, математическом анализе, теории чисел. [12, с.82-102]
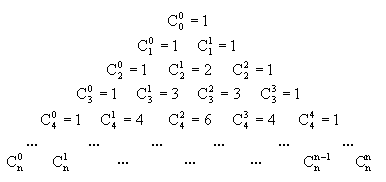
Рис.4. Общий вид треугольника Паскаля
Разделы комбинаторики
Как гласят источники «Дискретная математика и комбинаторика» Дж. Андерсона и «Комбинаторика» М. Холла, перечислительная или исчисляющая комбинаторика — это раздел комбинаторики, который рассматривает задачи о перечислении или подсчёте количества различных конфигураций, образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения и т. п. Типичным примером задач данного раздела является подсчёт количества перестановок.
Структурная комбинаторика — к данному разделу относятся некоторые вопросы теории графов – раздела дискретной математики, изучающего свойства графов – множества вершин и узлов, соединённых рёбрами. Также к структурной комбинаторике относятся теории матроидов. Матроид – это классификация подмножеств некоторого множества на произвольное множество.
Теория Рамсея — это теория, изучающая наличие регулярных структур в случайных конфигурациях элементов. Примером утверждения из теории Рамсея может служить следующая задача: «В группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы».
Вероятностная комбинаторика — это раздел дискретной математики, в котором методы теории вероятностей применяются для изучения комбинаторных объектов. В данном разделе рассматриваются также перечислительные задачи комбинаторики и вопросы существования комбинаторных объектов с заданными характеристиками. [3, с.564-569]
Топологическая комбинаторика — молодая область математики, возникшая в последней четверти 20-го века, которая занимается следующими вопросами:
Применение методов топологии при изучении древа принятия решений, частично упорядоченных множеств, раскрасок графа и т.д.
Топологические обобщения задач дискретной геометрии
Дискретизация топологических понятий
Инфинитарная комбинаторика — это раздел комбинаторики, реализующий идеи и методы комбинаторики для решения задач с бесконечными (в том числе, несчётными) множествами. [4, с.323-327]
глава 2. решение основных видов комбинаторных задач
В данной главе рассмотрены основные виды комбинаторных задач, приведены примеры для каждого типа, а также составлен собственный комплекс задач по каждой теме. Приведённую ниже классификацию комбинаторных задач указывают авторы Н. Алон и Дж. Спенсер. в источнике «Вероятностный метод: учебное пособие». [2, с.120-150]
Комбинаторные правила суммы и произведения
Если объект A можно выбрать из некоторого множества объектов m способами, а другой объект B – n способами, то выбор объекта A или объекта B (без разницы какого) возможен m + n способами.
Если объект A можно выбрать из некоторого множества объектов m способами и после каждого такого выбора объект B можно выбрать n способами, то упорядоченная пара объектов (A; B) может быть выбрана m ∙ n способами.
Важная содержательная часть правил состоит в том, знак «плюс» понимается и читается как союз ИЛИ, а знак «умножить» – как союз И.
Рассмотрим примеры задач на правило суммы и правило произведения
Решение: в этой задаче нужно выбрать одного юношу И одну девушку, поэтому будем использовать правило умножения.
Из 10 юношей одного можно выбрать 10 способами.
Из 13 девушек 13 способами можно выбрать одну.
10 ∙ 13 = 130 способами можно составить пару из юноши и девушки.
Сколько существует трёхзначных чисел, которые делятся на 5?
Решение:
В разряд сотен можно записать любую из цифр 1 – 9. Ноль не годится, так как в этом случае число перестаёт быть трёхзначным.
В разряд десятков можно выбрать любую из 10 цифр. По условию, число должно делиться на 5. Число делится на 5, если оно заканчивается на 5 либо на 0. Таким образом, в младшем разряде нас устраивают 2 цифры.
Так как цифры числа существуют вместе, то есть выбор одной цифры не исключает выбора второй, значит для решения данной задачи нужно воспользоваться правилом умножения.
Таким образом, 9 способами можно выбрать первую цифру.
Вторую цифру можно выбрать 10 способами.
Третью цифру можно выбрать только 2 способами.
Итого: 9 ∙ 10 ∙ 2 = 180 чисел, которые делятся на 5.
Решение:
Выигрывает комбинация десятка и туз (11 очков) = 21 очко. Союз «и» подсказывает нам, что для решения задачи снова придётся обратиться к правилу умножения.
Одну десятку из 4 имеющихся в колоде можно выбрать 4 способами.
Так как туза в колоде тоже четыре, для его выбора количество способов будет таким же, поэтому окончательный результат: 4 ∙ 4 = 16 выигрышных комбинаций.
Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола?
Решение: условие «выбрать двух человек одного пола» подразумевает, что необходимо выбрать двух юношей или двух девушек, значит для решения этой задачи нужно использовать правило суммы.
10 способами можно выбрать одного из 10 юношей, тогда как второго можно выбрать 9 способами, так как один юноша уже будет выбран. Но порядок их выбора не важен, поэтому полученный результат нужно разделить на 2. Итого, 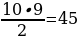 способами можно выбрать двух юношей.
способами можно выбрать двух юношей.
Таким же образом можно посчитать количество способов, которыми можно выбрать двух девушек: 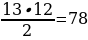 способами можно выбрать двух девушек.
способами можно выбрать двух девушек.
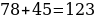 способами можно выбрать двух человек одного пола.
способами можно выбрать двух человек одного пола.
Приведённые в качестве примеров комбинаторные задачи были приведены в источнике «Алгебра и теория чисел. Сборник задач для математических школ» под редакцией Н. Б. Алфутовой и А. В. Устинова.
Перестановки, сочетания и размещения без повторений
В комбинаторных задачах на перестановки, сочетания и размещения без повторений обычно участвует множество, состоящее из какого-либо количества различных объектов, или же объектов, считающихся в контексте той или иной задачи различными.
Перестановки без повторений
Формула количества перестановок без повторений: 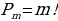
В общем виде смысл задачи можно сформулировать так: «Сколькими способами можно переставить m объектов?».
Рассмотрим примеры заданий на данный тип комбинаторных задач
Группа туристов за пять дней пребывания в Гагре может посетить Сухум, Альпийские луга, Каман, озеро Рица и экскурсию по ночной Гагре. Сколькими способами они могут сделать это?
Решение: 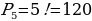 способами
способами
Веселые человечки построились в ряд: Незнайка, Знайка, Тобик, Винтик, Шпунтик, Кнопочка, Сиропчик, Цветик, Гунька, Ворчун, Пончик. Сколькими способами они могли это сделать?
Решение: 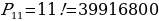 способами
способами
В морозильной камере лежат девять порций мороженого от различных фирм. Сколькими способами можно выбрать порядок их съедения?
Решение: 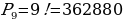 способами
способами
Сочетания без повторений
Формула количества сочетаний без повторений: 
В общем виде смысл задачи можно сформулировать так: «Сколькими способами можно выбрать m объектов из n?».
Рассмотрим примеры заданий на данный тип комбинаторных задач
На день рождения Лене подарили коробку конфет (в коробке 30 штук). Сколькими способами она может выбрать по одной конфете пятерым подругам?
Решение: 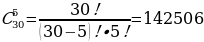 способами
способами
У Малыша есть 10 видов сладостей. Он предложил Карлсону выбрать 2 вида сладостей из этого списка. Между сколькими возможностями придется выбирать Карлсону?
Решение:  способами
способами
В «Лукойл» требуются 9 охранников. В агентстве «Альфа» есть 15 человек, подходящих на эту должность. Сколькими способами может быть набран отдел охраны «Лукойла»?
Решение: 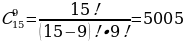 способами
способами
Размещения без повторений
Формула количества размещений без повторений:
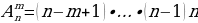
В общем виде смысл задачи можно сформулировать так: «Сколькими способами можно выбрать m объектов из n и в каждой выборке переставить их определенным образом?». Исходя из вышесказанного, справедлива следующая формула:

Рассмотрим примеры заданий на данный тип комбинаторных задач
Боря, Дима и Володя сели играть в «двадцать одно». Сколькими способами им можно сдать по одной карте?
Решение:  способами
способами
В цехе работают 8 токарей. Сколькими способами можно поручить трем из них изготовление различных видов деталей (по одному виду на каждого)?
Решение: 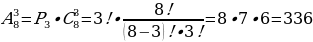 способами
способами
Студенты института изучают в каждом семестре по десять дисциплин. В расписание занятий включаются каждый день по 3 дисциплины. Сколько различных расписаний может составить диспетчерская?
Решение:  способами
способами
Перестановки, сочетания и размещения с повторениями
В комбинаторных задачах на перестановки, сочетания и размещения с повторениями обычно участвует множество, состоящее из какого-либо количества объектов, среди которых есть одинаковые (либо считающиеся таковыми по условию задачи).
Перестановки с повторениями
Формула количества перестановок с повторениями:
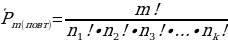 , где
, где 
В общем виде смысл задачи можно сформулировать так: «Количество способов, которыми можно переставить m объектов, среди которых один объект повторяется n1 раз, второй объект повторяется n2 раз, третий объект – n3 раз и т.д.?».
Рассмотрим примеры заданий на данный тип комбинаторных задач
Сколько различных буквосочетаний можно получить перестановкой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К??
Решение: 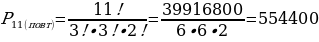 буквосочетаний
буквосочетаний
Алексей занимается спортом, причём четыре дня в неделю – лёгкой атлетикой, два дня – силовыми упражнениями и один день отдыхает. Сколькими способами он может составить себе расписание занятий на неделю?
Решение:  способами
способами
Сколькими способами можно собрать гирлянду из 4 красных, 4 синих и 8 желтых флажков?
Решение: 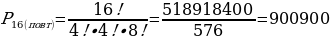 способами
способами
Сочетания с повторениями
Формула количества сочетаний с повторениями:

В общем виде смысл задачи можно сформулировать так: «Для выбора предложено n множеств, каждое из которых состоит из одинаковых объектов. Сколькими способами можно выбрать m объектов?».
Рассмотрим примеры заданий на данный тип комбинаторных задач
В студенческой столовой продают сосиски в тесте, пирожки с капустой и пирожки с яйцом и зелёным луком. Сколькими способами можно приобрести пять единиц выпечки?
Решение: 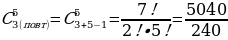 = 21 способом
= 21 способом
В кошельке находится достаточно большое количество однорублёвых, двухрублёвых, пятирублёвых и десятирублёвых монет. Сколькими способами можно извлечь три монеты из кошелька?
Решение: 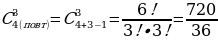 = 20 способами
= 20 способами
 ?
?
Решение:
Переформулируем задачу в терминах комбинаторики. Пусть у нас есть m=8 условных единиц, их нужно разместить в n=4 условных ёмкостях. Так как решение требуется в неотрицательных числах, то ёмкость в том числе может быть пустой.
Применяем формулу числа сочетаний с повторениями:
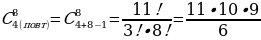 = 165 решений
= 165 решений
Размещения с повторениями
Формула количества размещений с повторениями: 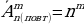
В общем виде смысл задачи можно сформулировать так: ««Дано множество, состоящее из n объектов, при этом любой объект можно выбирать неоднократно. Сколькими способами можно выбрать m объектов, если важен порядок их расположения в выборке? »
Рассмотрим примеры заданий на данный тип комбинаторных задач
Сколько существует четырёхзначных пин-кодов? (Учитывая, что для пин-кода используются цифры от 0 до 9, то есть всего их десять).
Решение: 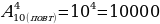 пин-кодов
пин-кодов
В лифт 8-этажного дома вошли четыре пассажира. Сколькими способами они могут выйти (выход возможен на любом этаже, начиная со второго)?
Решение: 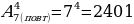 способом
способом
Решение: пусть у нас есть m=5 нечётных цифр (1,3,5,7,9). Их нужно расставить на n=3 места, т.к. число трёхзначное, тогда:
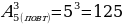 трехзначных чисел.
трехзначных чисел.
Комплекс задач на применение формул комбинаторики
Перестановки без повторений
На столе лежат фрукты – киви, яблоко и банан. Сколькими способами можно их переложить?
Решение: 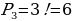 способами.
способами.
На книжной полке в библиотеке стоят пять книг разных авторов. Сколькими способами библиотекарь может их переставить?
Решение: 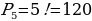 способами.
способами.
Настя поехала в отпуск на четыре дня и взяла с собой четыре платья. Сколькими способами она сможет носить свои платья, при условии, что один день она ходит только в одном платье?
Решение:  способами.
способами.
Сочетания без повторений
На столе лежат фрукты – киви, яблоко и банан. Сколькими способами можно выбрать два фрукта?
Решение: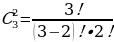 = 3 способами.
= 3 способами.
На книжной полке в библиотеке стоят пять книг разных авторов. Сколькими способами библиотекарь может выбрать четыре книги?
Решение: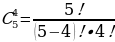 = 5 способами.
= 5 способами.
Настя поехала в отпуск на четыре дня и взяла с собой четыре платья. Сколькими способами она может выбрать три платья?
Решение: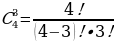 = 4 способами.
= 4 способами.
Размещения без повторений
На столе лежат фрукты – киви, яблоко и банан. Сколькими способами можно раздать по одному фрукту Пете и Васе?
Решение: 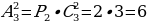 способами.
способами.
На книжной полке в библиотеке стоят пять книг разных авторов. Сколькими способами библиотекарь может дать по две книги двум посетителям?
Решение: 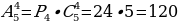 способами.
способами.
Настя поехала в отпуск на четыре дня и взяла с собой четыре платья. Сколькими способами она может дать трём подругам по одному платью?
Решение:  способами.
способами.
Перестановки с повторениями
Имеется восемь шаров различных цветов. Сколькими способами можно разложить шары в три коробки так, чтобы в первой коробке было 3 шара, во второй четыре, а в третьей - один?
Решение: 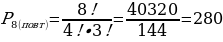 способами.
способами.
Сколькими способами можно разбить группу из пяти активных студентов на двух декораторов, двух сценаристов и одного артиста?
Решение: 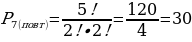 способами.
способами.
Сколькими способами можно расставить белые фигуры: двух коней, двух слонов, две ладьи, ферзя и короля на первой линии шахматной доски, учитывая, что длина этой линии 8 клеток?
Решение:  способами.
способами.
Сочетания с повторениями
Имеются шары трёх различных цветов: красные, синие и жёлтые. Сколькими способами можно достать десять шаров?
Решение:  способами.
способами.
Для участия в мероприятии студенту нужно записаться в одну из трёх групп: сценаристы, декораторы, артисты. Сколькими способами семь студентов смогут записаться в группы?
Решение: 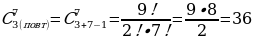 способами.
способами.
На шахматной доске расставлены фигуры четырёх видов: кони, слоны, ладьи и пешки. Сколькими способами можно выбрать 9 фигур?
Решение: 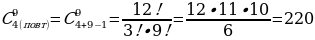 способами.
способами.
Размещения с повторениями
Имеется пять различных шаров, их нужно разложить по двум различным ящикам (на число шаров в ящиках ограничений нет – ящик может вместить как все шары, так и остаться пустым). Сколькими способами можно это сделать?
Решение:  способами.
способами.
Девять незанятых студентов нужно распределить по трём группам: сценаристы, артисты и декораторы. Распределение может быть любым. Сколькими способами это можно сделать?
Решение:  способами.
способами.
Сколькими способами можно расставить все белые пешки (8 штук) на двух шахматных линиях? Расстановка может быть любой.
Решение:  способами.
способами.
Комбинаторные правила суммы и произведения
В кафе подают 6 видов молочных коктейлей и 10 видов соков. Сколькими способами можно заказать напиток в этом кафе? (Заказать можно только один вид напитка).
Решение: в данной задаче нужно выбрать только один вид напитка, поэтому полученные результаты нужно будет сложить, чтобы найти ответ.
Один вид сока из 10 предложенных можно выбрать 10 способами.
Один вид молочного коктейля из 6 предложенных — 6 способами.
10 + 6 = 16 способов заказать напиток в этом кафе.
Немного изменим условие. В кафе подают 6 видов выпечки и 10 видов соков. Сколькими способами можно сделать заказ, который будет состоять из выпечки и сока?
Решение: нам нужно просчитать комбинации, в которой участвует обязательно и выпечка, и сок, поэтому будем использовать правило умножения.
Один вид сока из 10 предложенных можно выбрать 10 способами.
Один вид выпечки из 6 предложенных — 6 способами.
10 ∙ 6 = 60 способов заказать выпечку и сок в этом кафе.
Сколько можно составить чётных двухзначных чисел?
Решение: по аналогии с рассмотренной в примерах задачей, будем применять правило комбинаторного умножения. Первую цифру числа можем выбрать из 9 цифр (1-9), так как ноль не подходит. Вторая цифра должна быть чётной, поэтому нам подойдут пять цифр – 0, 2, 4, 6 и 8.
Таким образом, выбрать первую цифру можно 9 способами.
Вторую цифру – 5 способами.
Итого: 9 ∙ 5 = 45 способов составить чётных двухзначных чисел.
заключение
Итак, материалом для проведённого исследования послужили виды комбинаторных задач и методов их решения. Актуальность исследования была обусловлена важностью комбинаторики как науки и её использованием в различных сферах жизни человека. В первой главе настоящей курсовой работы приведены доказательства данных утверждений.
В данной курсовой работе была поставлена и достигнута следующая цель: изучение методов решения основных видов комбинаторных задач и составление собственного комплекса задач. Также была проанализирована математическая и историческая литература, состоящая из пятнадцати источников, систематизированы полученные данные, выявлены основные виды комбинаторных задач и методы их решения, подобраны соответствующие примеры заданий и составлен комплекс собственных задач.
Как показало проведённое исследование, комбинаторика зародилась ещё до нашей эры. Данную науку использовали повсеместно: и при анализе головоломок, и для побед в азартных играх, и в торговле, и в астрологии и т.д.
Изучением комбинаторики занимались выдающиеся учёные такие, как Блез Паскаль, Пьер Ферма, Джероламо Кардано, Якоб Бернулли, Леонард Эйлер и многие другие.
Значение комбинаторики в настоящее время сложно переоценить. Она разнообразна и многогранна, поэтому встречается как в повседневных вопросах (рассадка гостей, составление расписания), так и в самых сложных технических расчётах. Данная наука стремительно развивается, и всё больше задач из различных областей можно решить с помощью комбинаторных методов.
Практическая ценность исследования заключается в составленном комплексе заданий по каждому виду комбинаторных задач. Данный комплекс заданий может быть использован в дальнейшем при работе с учащимися учебных заведений различного уровня подготовки.
Исследование данной темы может быть продолжено в нескольких направлениях. Например, вопрос комбинаторики может быть рассмотрен с точки зрения методики её преподавания. Также, в рамках данной темы можно разработать игровой комплекс заданий, который поможет в дальнейшем облегчить изучение некоторых видов комбинаторных задач.
Комбинаторика тесно связана с такой наукой, как теория вероятностей, поэтому ещё одним возможным шагом дальнейшего исследования может стать исследовательская работа по теории вероятностей.
список литературы
Алгебра и теория чисел. Сборник задач для математических школ / Н.Б. Алфутова, А.В. Устинов. — М.: МЦНМО, 2002. — 264 с.
Вероятностный метод: учебное пособие [Электронный ресурс] / Н. Алон, Дж. Спенсер. Пер. с англ. — М.: Бином. Лаборатория знаний, 2013. — 320 с.
Дискретная математика и комбинаторика / Дж. Андерсон. Пер. с англ. — М.: Изд-во Вильямс, 2006. — 960 с.
Комбинаторика / М. Холл. Пер. с англ. — М.: Мир, 1970. — 421 с.
Комбинаторика / Н. Я. Виленкин, А. Н. Виленкин, П. А. Виленкин. — М.: ФИМА, МЦНМО, 2017. — 400 с.
Комбинаторика в жизнедеятельности человека и решение комбинаторных задач / И. И. Роганова // Международный журнал гуманитарных и естественных наук. Педагогические науки. — 2018. — № 3. — С. 20-25.
Конкретная математика. Основание информатики / Р. Грэхем, Д. Кнут,
О. Паташник. Пер. с англ. — М.: Мир, 1998. — 703 с.
Математика XVII столетия // История математики / А. П. Юшкевич,
в трёх томах. — М.: Наука, 1970. — Т. II. — 301 с.
Математика XVIII столетия // История математики / А. П. Юшкевич,
в трёх томах. — М.: Наука, 1972. — Т. III. — 496 с.
Об исследовании Леонардом Эйлером латинских квадратов/ А. Е. Малых, А. С. Каленкова // Вестник ПГГПУ. Серия № 2. Физико-математические и естественные науки. — 2017. — № 1. — С. 102-116.
Популярная комбинаторика / Н. Я. Виленкин. — М.: Наука, 1975. — 208с.
Развитие некоторых классических комбинаторных задач / А. Е. Малых, А.А. Давыдова // Вестник ПГГПУ. Серия № 2. Физико-математические и естественные науки. — 2017. — № 1. — С. 82-102.
С древнейших времен до начала Нового времени // История математики / А. П. Юшкевич, в трёх томах. — М.: Наука, 1970. — Т. I. — 352 с.
Статистика. Вероятность. Комбинаторика / Я. С. Бродский. — М.: Оникс, Мир и Образование, 2008. — 544 с.
Теоремы и задачи комбинаторной геометрии / В. Г. Болтянский,
И. Ц. Гохберг. — М.: Наука, 1965. — 108 с.
1





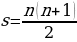 . Число n называют порядком магического квадрата. Доказано, что магический квадрат можно построить для любого
. Число n называют порядком магического квадрата. Доказано, что магический квадрат можно построить для любого  .
.


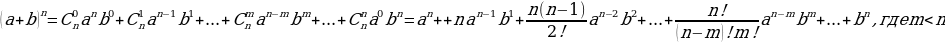
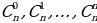 – биномиальные коэффициенты, полученные с использованием операции сложения с помощью треугольника Паскаля.
– биномиальные коэффициенты, полученные с использованием операции сложения с помощью треугольника Паскаля.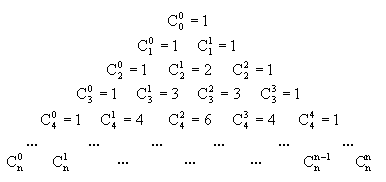
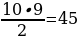 способами можно выбрать двух юношей.
способами можно выбрать двух юношей.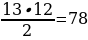 способами можно выбрать двух девушек.
способами можно выбрать двух девушек.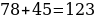 способами можно выбрать двух человек одного пола.
способами можно выбрать двух человек одного пола.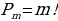
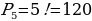 способами
способами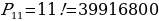 способами
способами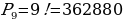 способами
способами
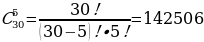 способами
способами способами
способами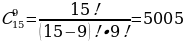 способами
способами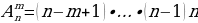

 способами
способами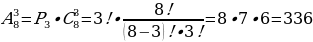 способами
способами способами
способами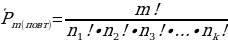 , где
, где 
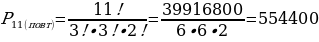 буквосочетаний
буквосочетаний  способами
способами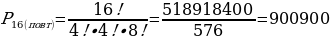 способами
способами
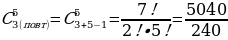 = 21 способом
= 21 способом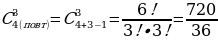 = 20 способами
= 20 способами ?
?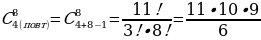 = 165 решений
= 165 решений 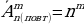
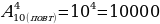 пин-кодов
пин-кодов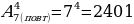 способом
способом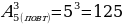 трехзначных чисел.
трехзначных чисел.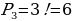 способами.
способами. способами.
способами.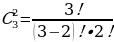 = 3 способами.
= 3 способами.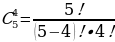 = 5 способами.
= 5 способами.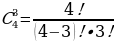 = 4 способами.
= 4 способами.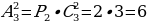 способами.
способами.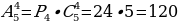 способами.
способами. способами.
способами.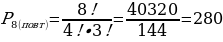 способами.
способами.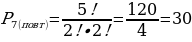 способами.
способами. способами.
способами. способами.
способами.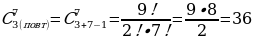 способами.
способами.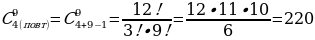 способами.
способами. способами.
способами. способами.
способами. способами.
способами.
















