Комбинация шара с другими телами.

КОМБИНАЦИЯ ШАРА С ДРУГИМИ ТЕЛАМИ

I. Некоторые геометрические места точек

Перед тем, как приступать к вопросу о комбинации шара с другими телами, следует повторить некоторые геометрические места точек, изученные в курсе геометрии .

ГМТ-1. Геометрическое место точек, равноудалённых от двух данных точек, есть плоскость, перпендикулярная к отрезку с концами в данных точках и проходящая через его середину.

ГМТ-2. Геометрическое место точек, равноудалённых от двух параллельных между собой плоскостей, есть плоскость, параллельная данным и проходящая через середину расстояния между ними.

ГМТ-3. Геометрическое место точек, равноудалённых от граней двугранного угла, есть плоскость, делящая этот двугранный угол пополам. Такая плоскость называется биссекторной.

ГМТ-4. Геометрическое место точек, равноудалённых от всех точек окружности, есть прямая, перпендикулярная плоскости этой окружности, проходящая через её центр.

Следствие. Геометрическое место точек, равноудалённых от всех вершин многоугольника, вписанного в окружность, есть прямая, перпендикулярная плоскости этого многоугольника и проходящая через центр окружности

II. Определения

1. Шар называется вписанным в многогранник, а многогранник описанным около шара, если поверхность шара касается всех граней многогранника.

2. Шар называется описанным около многогранника, а многогранник вписанным в шар, если поверхность шара проходит через все вершины многогранника

3. Шар называется вписанным в цилиндр, усеченный конус (конус), а цилиндр, усеченный конус (конус) – описанным около шара, если поверхность шара касается оснований (основания) и всех образующих цилиндра, усеченного конуса (конуса).

(Из этого определения следует, что в любое осевое сечение этих тел может быть вписана окружность большего круга шара).

1. Шар называется описанным около цилиндра, усеченного конуса (конуса), если окружности оснований (окружность основания и вершина) принадлежат поверхности шара. (Из этого определения следует, что около любого осевого сечения этих тел может быть описана окружность большего круга шара).

III. Общие замечания о положении центра шара

1. Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника

2. Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника.

IV. Комбинация шара с призмой

1. Шар, вписанный в прямую призму

Теорема 1. Шар можно вписать в прямую призму в том и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности.

Доказательство необходимости

Д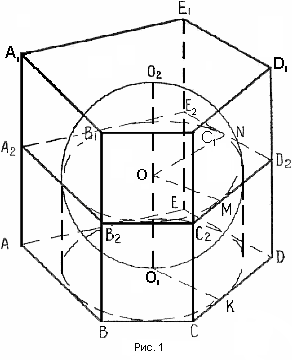 опустим, что в некоторую прямую призму вписан шар (рис. №1).Докажем, что в основание этой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. Из центра шара, точки О, проведём радиусы OM и ON в точки касания шара с граням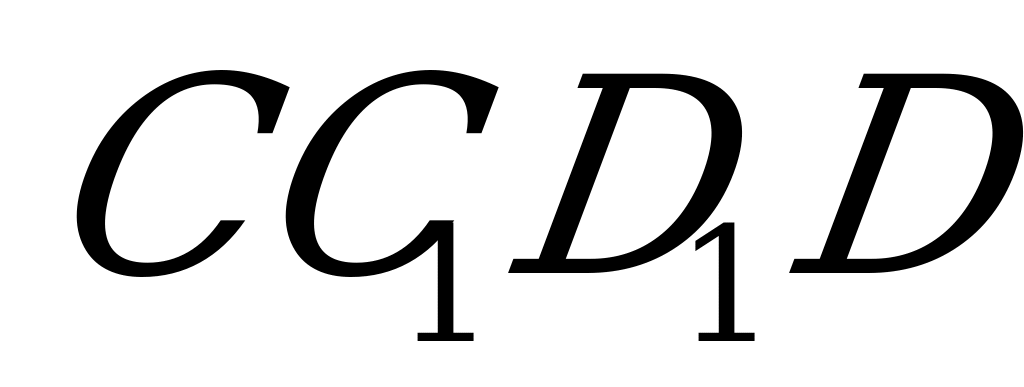и и 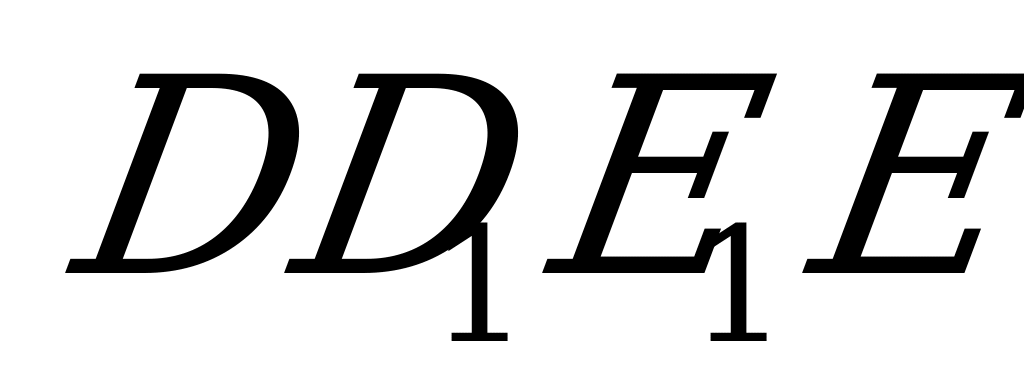. Тогда эти радиусы будут перпендикулярны боковым граням (теорема о свойстве радиуса, проведённого в точку касания шара с плоскостью). Через OM и ON проведём плоскость 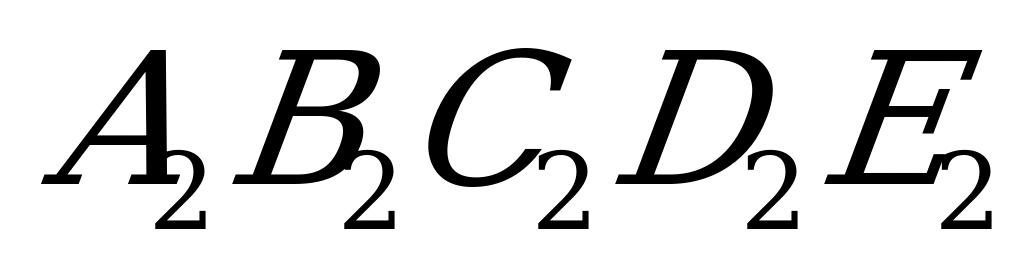. Эта плоскость перпендикулярна указанным граням (признак перпендикулярности плоскостей) и линии их пересечения (следствие из признака перпендикулярности плоскостей), а следовательно, перпендикулярна остальным боковым ребрам как параллельным , а потому перпендикулярна и всем боковым граням.

Если из точки О опустим перпендикуляры на остальные боковые грани, то все они будут лежать в плоскости 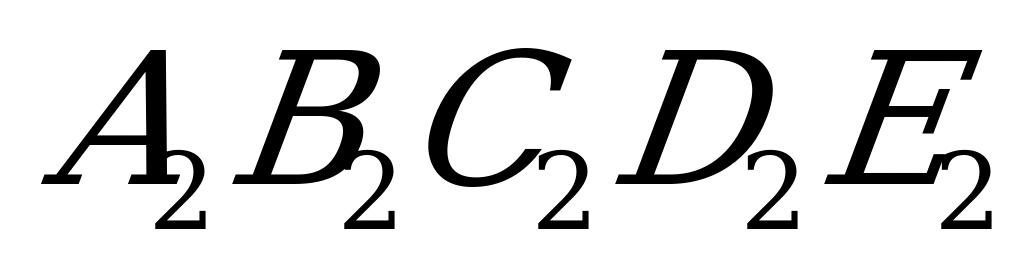(теорема о прямой, перпендикулярной к одной из перпендикулярных плоскостей, имеющей общую точку с другой).

Таким образом, точка О равноудалена от всех сторон перпендикулярного сечения, т. е. служит центром окружности, вписанной в перпендикулярное сечение. Но это сечение равно основанию. Поэтому в основание тоже можно вписать окружность с радиусом, равным радиусу шара. Радиусы 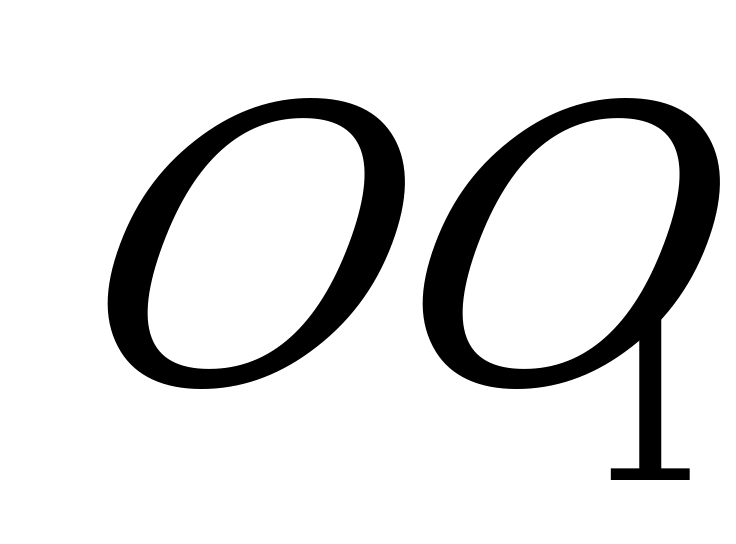и 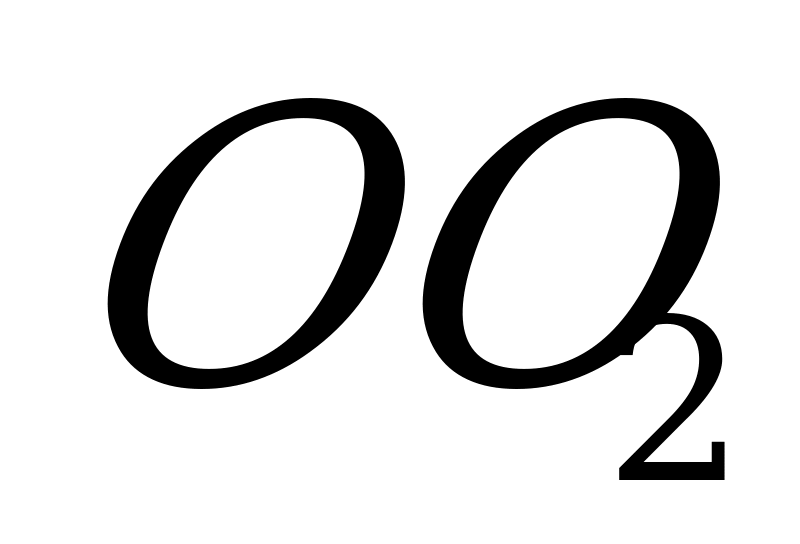, где точк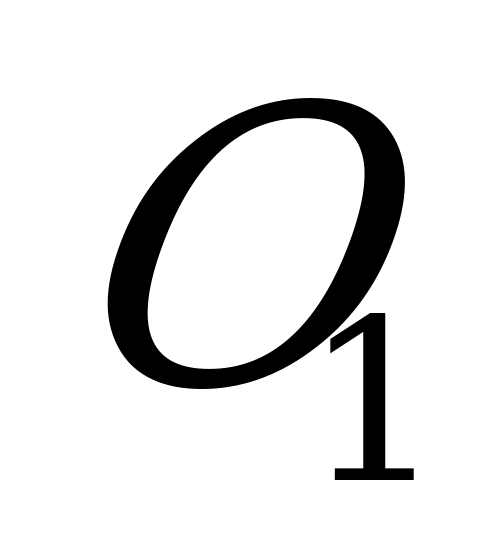и и 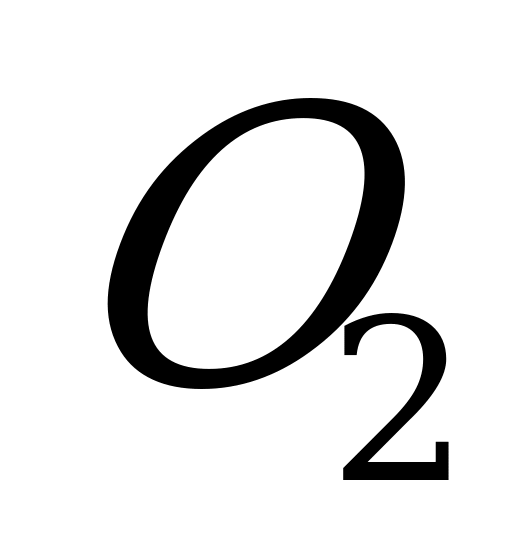- точки касания шара с основанием, будучи перпендикулярными к параллельным между собой плоскостям, составят отрезок 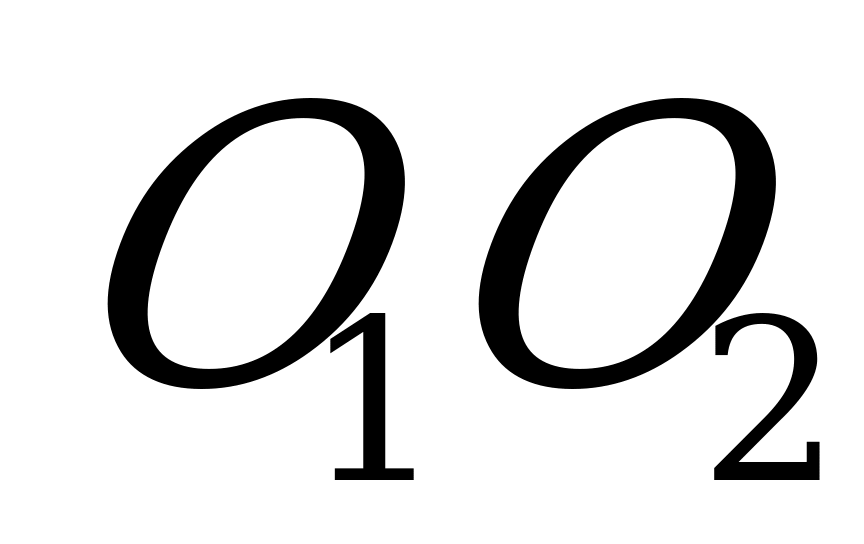, перпендикулярный основаниям, а потому высота призмы равна диаметру шара или диаметру окружности, вписанной в основание.

Доказательство достаточности

Допустим, что в основание прямой призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. Докажем, что в эту призму можно вписать шар, т. е. существует точка, равноудаленная от всех граней этой призмы.

Проведём прямую 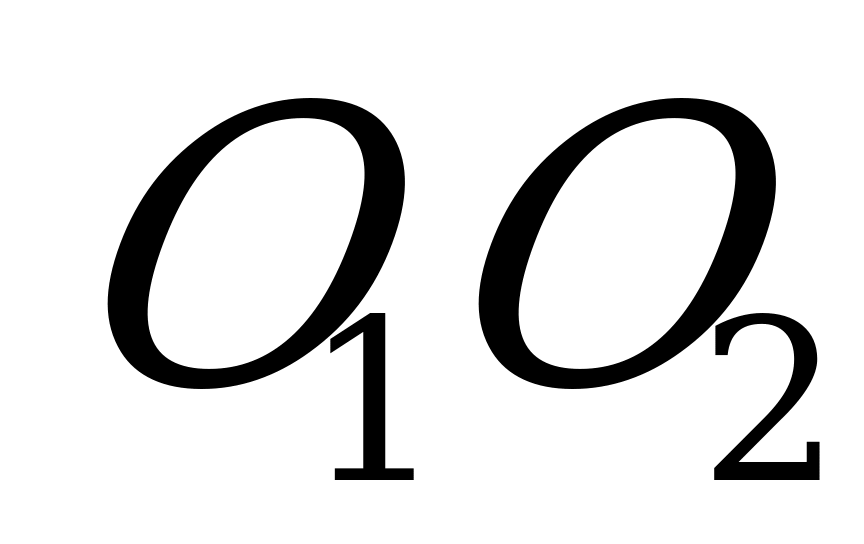через центр окружности, вписанной в основание призмы, перпендикулярно этому основанию. Прямая 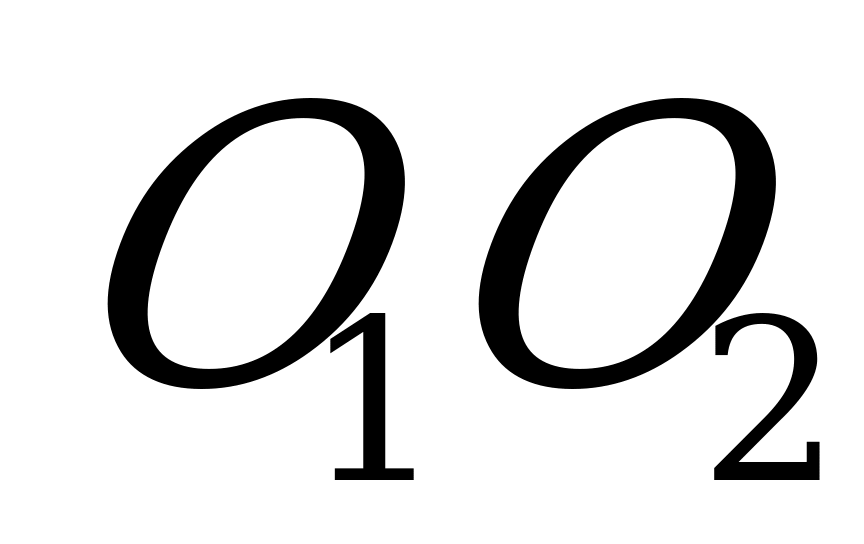параллельна каждому боковому ребру (теорема о двух прямых, перпендикулярных к одной плоскости), а потому она параллельна каждой боковой грани (признак параллельности прямой и плоскости). Радиус 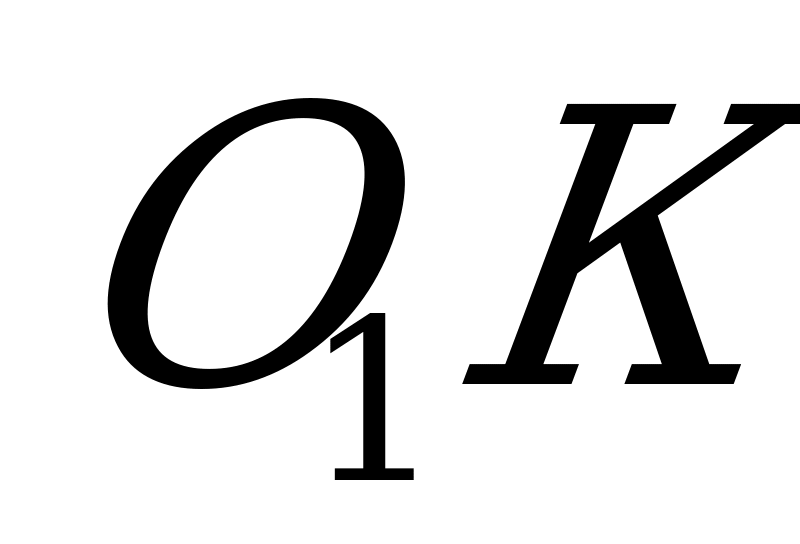, проведённый в точку касания К, перпендикулярен CD и 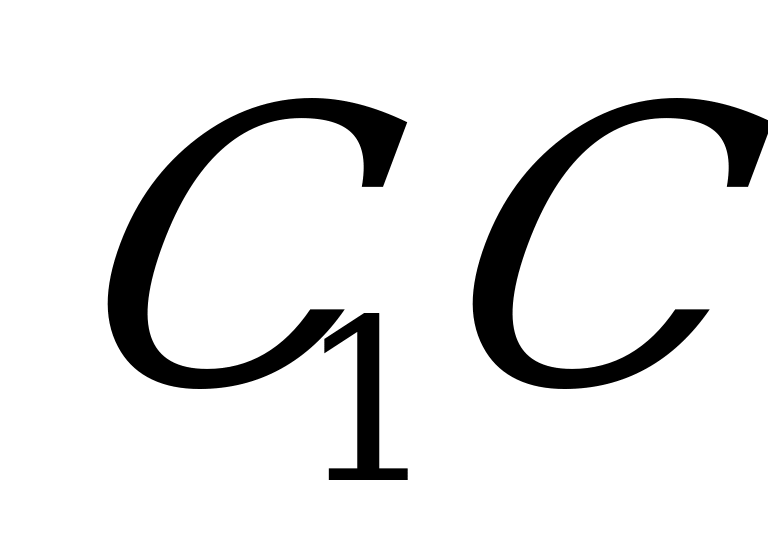, а потому перпендикулярен грани 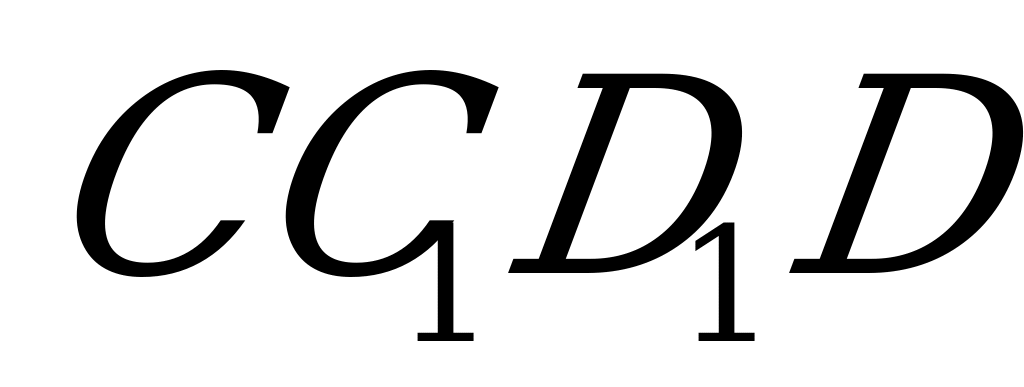(признак перпендикулярности прямой и плоскости). Следовательно, прямая 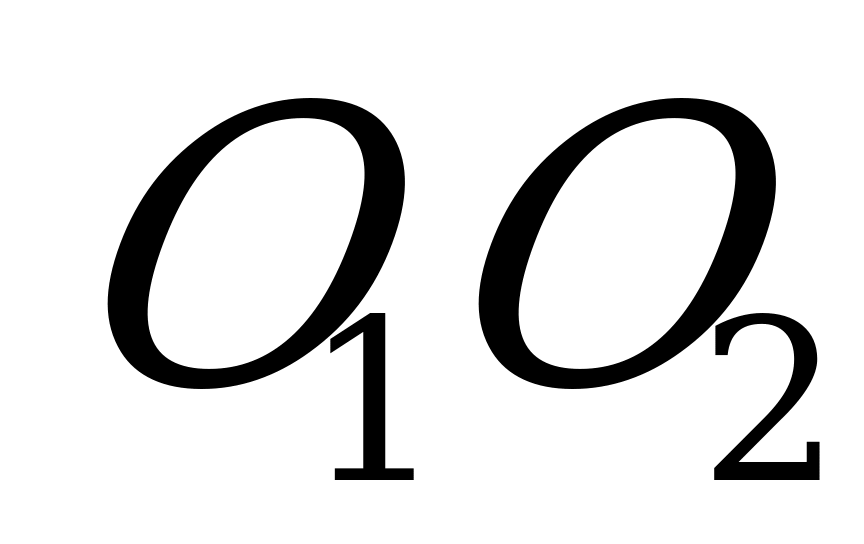удалена от каждой боковой грани на величину радиуса окружности, вписанной в основание призмы. Поэтому, если существует точка, равноудаленная от всех граней призмы, то она должна принадлежать отрезку .

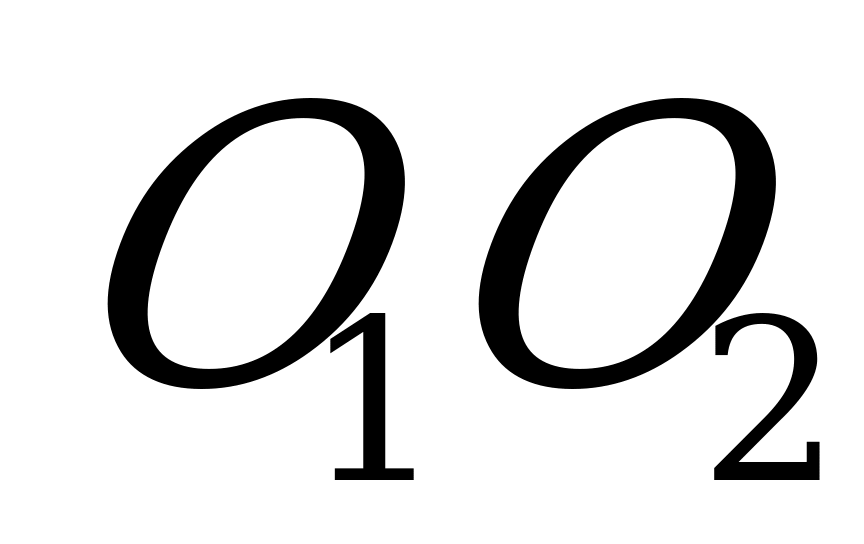По условию высота призмы 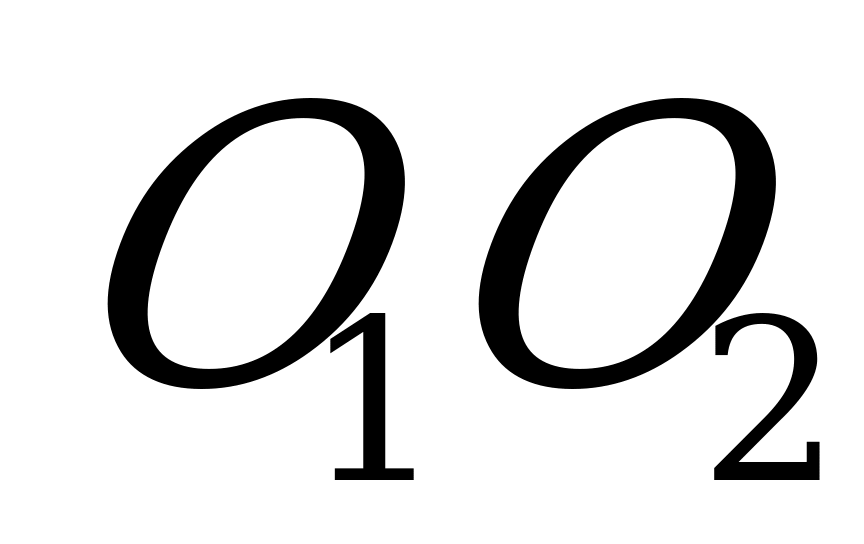равна диаметру окружности, вписанной в основание призмы, а потому середина отрезка 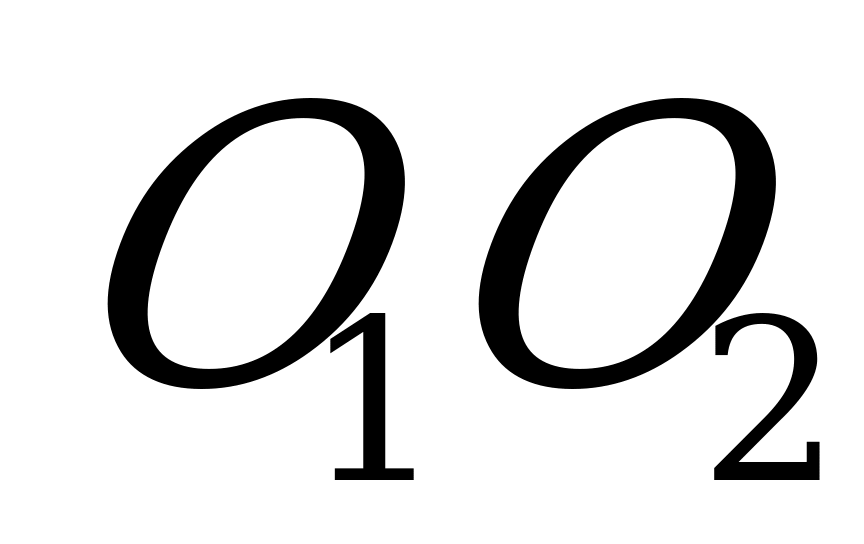и есть точка, равноудаленная от всех граней призмы, т. е. будет служить центром шара, вписанного в эту призму. Эта точка единственная. Это доказательство справедливо для призм с любым числом сторон основания.

Следствие 1. Центр шара, вписанного в прямую призму, лежит в середине высоты призмы, проходящей через центр окружности, вписанной в основание.

Следствие 2. Шар, в частности, можно вписать в прямые призмы: треугольную, правильную, четырехугольную (у которой суммы противоположных сторон основания равны между собой) при условии H=2r, где Н – высота призмы, r – радиус круга, вписанного в основание.

1. Шар, описанный около призмы

Теорема 2. Шар можно описать около призмы в том и только в том случае, если призма прямая и около её основания можно описать окружность.

Доказательство необходимости

Д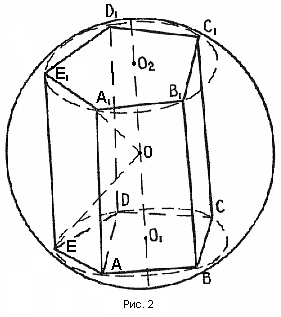 опустим, что шар описан около призмы (рис. №2). Докажем, что призма прямая и что около её основания можно описать окружность.

Плоскость основания призмы (теорема о сечении шара плоскостью) пересечет поверхность шара по окружности, на которой лежат все вершины основания. Таким образом, около основания призмы можно описать окружность.

Плоскости любых боковых граней призмы также пересекут поверхность шара по окружностям, а так как из параллелограммов можно вписать в окружность только прямоугольник, то, следовательно, все боковые грани призмы – прямоугольники. Тогда боковое ребро, например 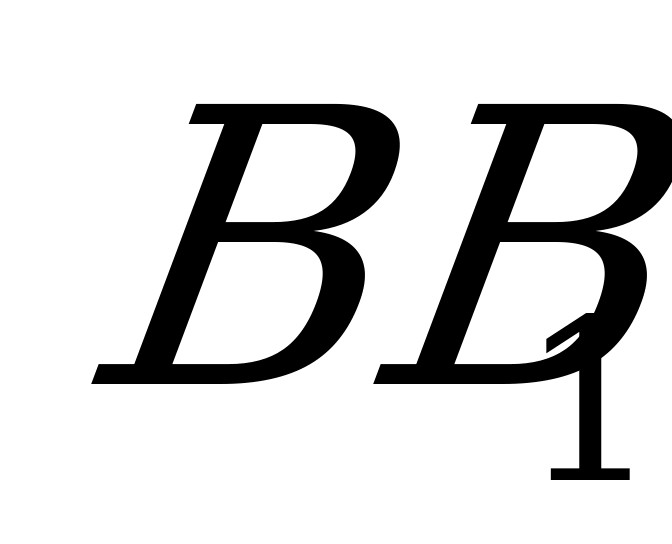, перпендикулярно к АВ и ВС, а потому (признак перпендикулярности прямой и плоскости) 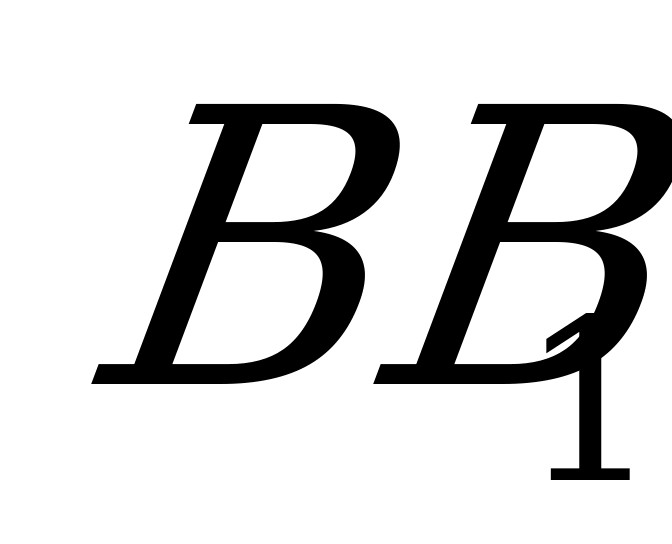перпендикулярно к плоскости основания. Значит, призма прямая.

Доказательство достаточности

Допустим, что около основания прямой призмы можно описать окружность, и докажем, что около такой призмы можно описать шар, т. е. существует точка, равноудаленная от всех вершин этой призмы. Так как основания призмы равны, то и окружности, описанные около них, равны. Из центра окружности, описанной около верхнего основания 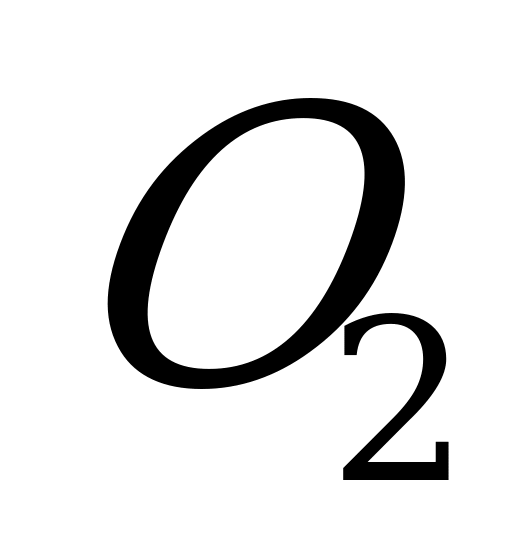, опустим перпендикуляр на нижнее основание 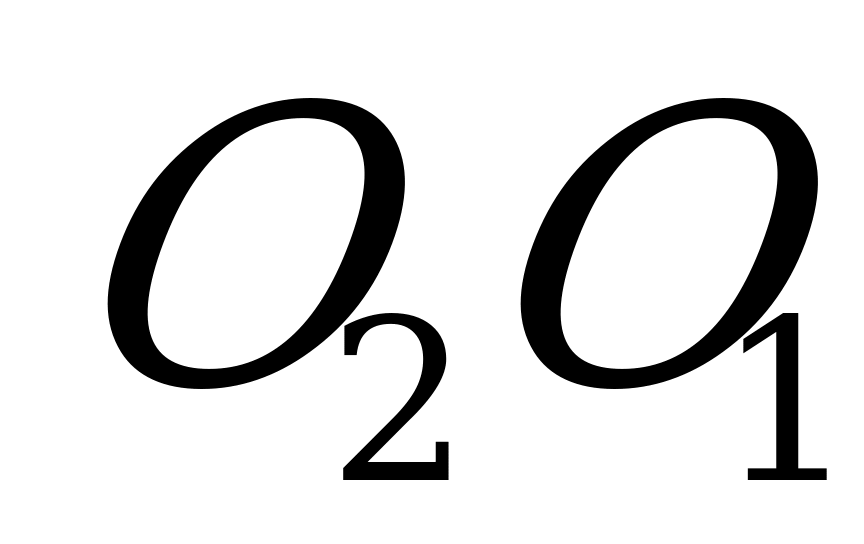. Четырехугольники 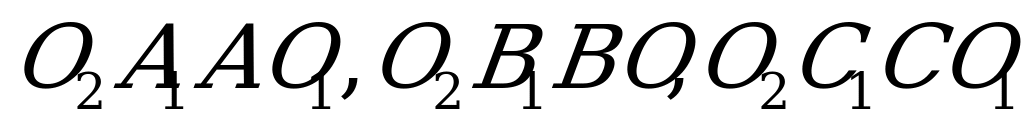и т.д. – прямоугольники, а потому из равенства: 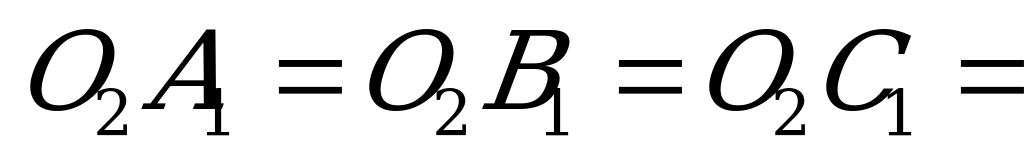… следуют равенства: 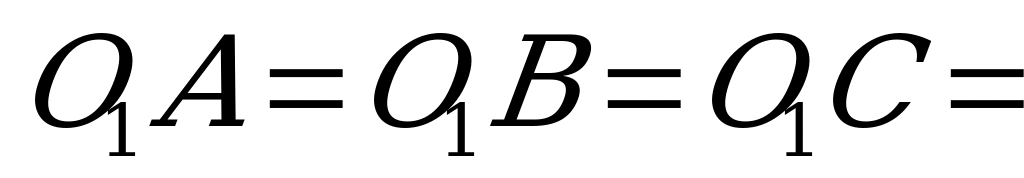… , т.е. точка 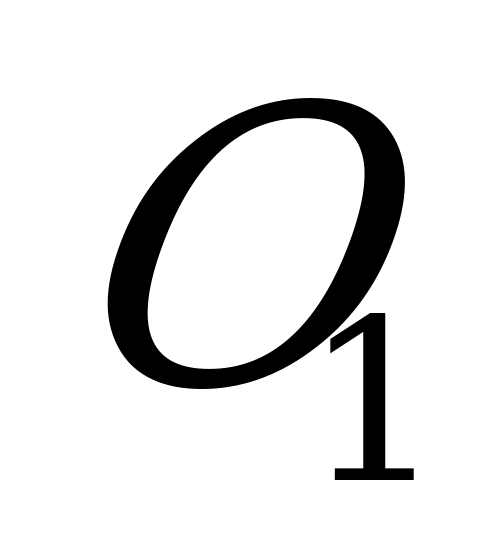является центром окружности, описанной около нижнего основания. Поэтому прямая 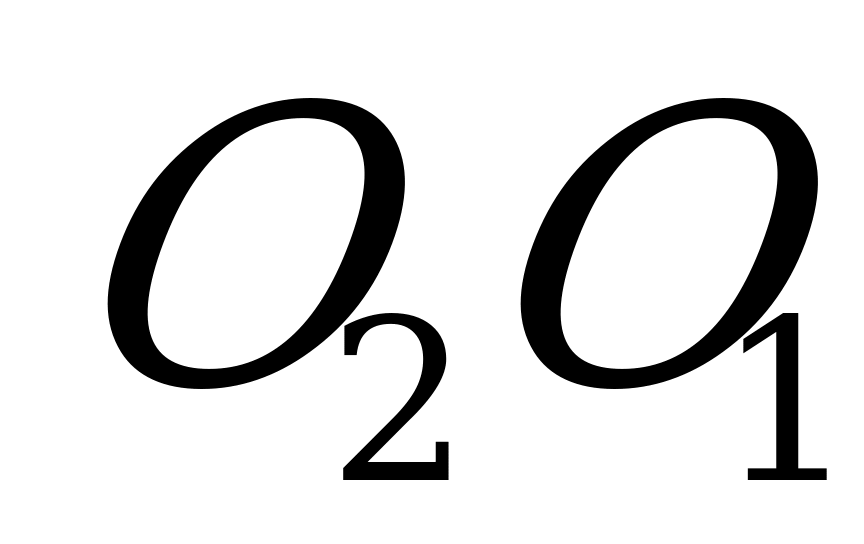, проходящая через центры окружностей, описанных около оснований, перпендикулярна основаниям. Все точки прямой 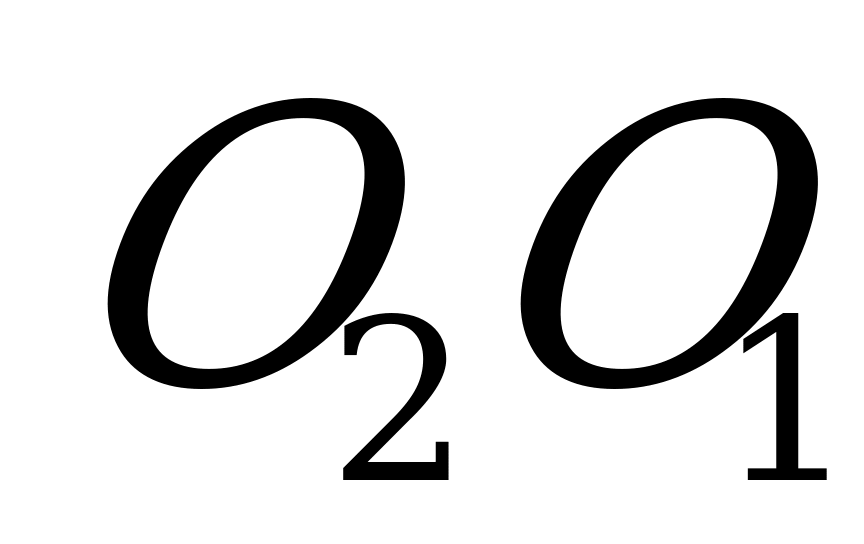равноудалены от вершины каждого основания (следствие из ГМТ-4). С другой стороны, все точки плоскости, проведенной через середины боковых ребер равноудалены от каждой пары вершин одного бокового ребра призмы, например, (ГМТ-1).

Пересечение этих геометрических мест даст единственную точку О, равноудаленную от всех вершин призмы, т.е. центр шара, описанного около призмы.

Следствие 1. Центр шара, описанного около прямой призмы, лежит на середине высоты призмы, проведенной через центр круга, описанного около основания.

Следствие 2. Шар, в частности можно описать: около прямой треугольной призмы, около правильной призмы, около прямоугольного параллелепипеда, около прямой четырехугольной призмы, у которой сумма противоположных углов основания равна 180.

V. Комбинация шара с пирамидой

Лемма. Через окружность и точку, не принадлежащую плоскости этой окружности, можно провести сферу и притом только одну.

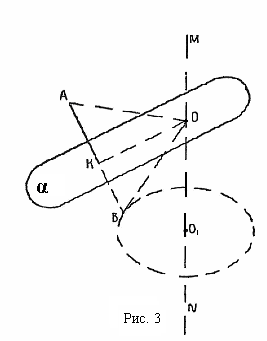
Геометрическое место точек, равноудаленных от всех точек окружности (ГМТ-4), есть прямая MN, перпендикулярная плоскости этой окружности и проходящая через ее центр (см. рис. № 3).

Возьмем на данной окружности произвольную точку В. Геометрическое место точек, равноудаленных от точек А и В (ГМТ-1), есть плоскость , перпендикулярная отрезку АВ и проходящая через его середину – точку К.

Точка пересечения этой плоскости  с MN – точка О, равноудалена от всех точек окружности и точки А, а потому является центром сферы, проходящей через окружность и точку А. Точка О есть единственная точка, обладающая этим свойством. Так как плоскость  пересекается с MN только в одной точке, а следовательно, через окружность и точку, не принадлежащую плоскости этой окружности, можно провести сферу и притом только одну.

1. Шар, описанный около пирамиды

Теорема 3. Около пирамиды можно описать шар в том и только в том случае, если около ее основания можно описать окружность

Доказательство необходимости

Допустим, что шар описан около пирамиды (рис. № 4). 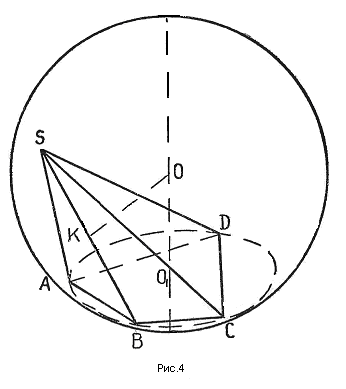Докажем, что около основания этой пирамиды можно описать окружность. Плоскость основания пересекает поверхность сферы по окружности (теорем о сечении шара плоскостью). Вершины основания лежат на поверхности шара и на плоскости основания, следовательно, они лежат на линии пересечения их, т.е. на окружности. Поэтому около основания можно описать окружность.

Доказательство достаточности

Допустим, что около основания пирамиды можно описать окружность.

Докажем, что около такой пирамиды можно описать шар. Вершины основания принадлежат окружности, а через окружность и точку S, расположенную вне плоскости этой окружности, на основании леммы, можно описать сферу и притом только одну. Следовательно, около этой пирамиды можно описать шар.

Следствие 1. Центр шара, описанного около пирамиды, лежит в точке пересечения прямой, перпендикулярной основанию пирамиды, проходящей через центр окружности, описанной около этого основания, и плоскости, перпендикулярной любому боковому ребру, проведенной через середину этого ребра.

С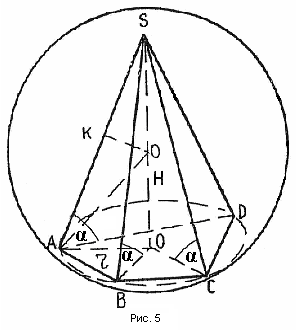 ледствие 2. Если боковые ребра пирамиды равны между собой (или равнонаклонены к плоскости основания), то около такой пирамиды можно описать шар (рис. № 5). Центр шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.

Известно, что если боковые ребра пирамиды равны, то вершина пирамиды проектируется в центр круга, описанного около основания. А так как около основания пирамиды можно описать окружность, то по доказанному выше, около такой пирамиды можно описать шар.

В этом случае полезно пользоваться формулами:

1)

2)

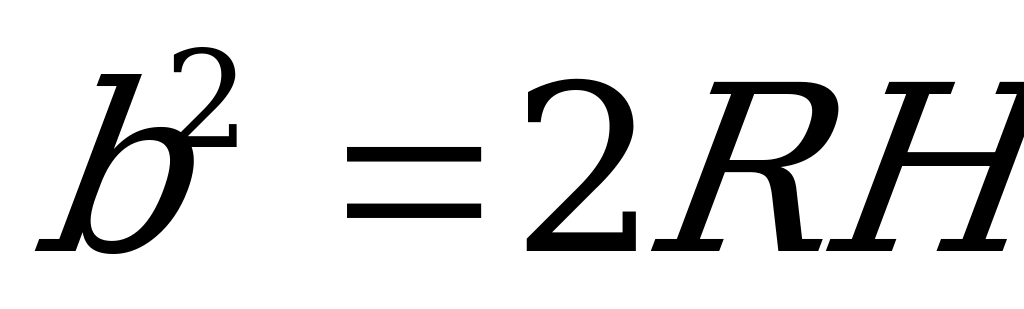
3)

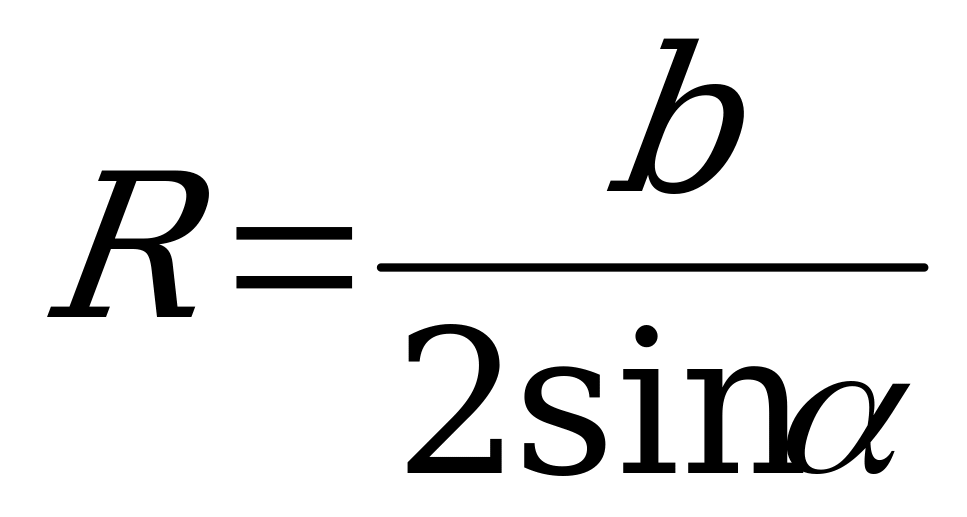
4) ,

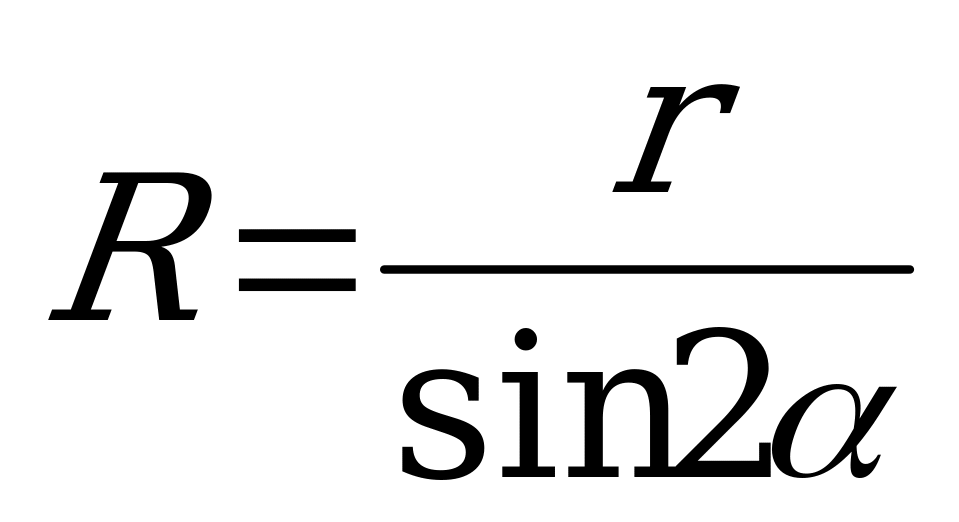где R – радиус шара, r – радиус окружности, описанной около основания пирамиды, b – боковое ребро, Н – высота пирамиды, α – угол наклона бокового ребра к плоскости основания.

Следствие 3. Шар, в частности, можно описать: около треугольной пирамиды, около правильной пирамиды, около четырехугольной пирамиды, у которой сумма противоположных углов равна 180.

1. Шар, вписанный в пирамиду

Шар можно вписать в выпуклую пирамиду в том и только в том случае, если биссекторные плоскости двугранных углов при всех боковых ребрах пересекаются по одной прямой или биссекторные плоскости всех двугранных углов при основании пирамиды проходят через одну точку.

Следствие 1. Шар можно вписать в любую треугольную пирамиду.

Следствие 2. Для того, чтобы шар можно было вписать в выпуклую четырехугольную пирамиду, необходимо и достаточно чтобы сумма плоских углов противоположных боковых граней пирамиды были равны между собой.

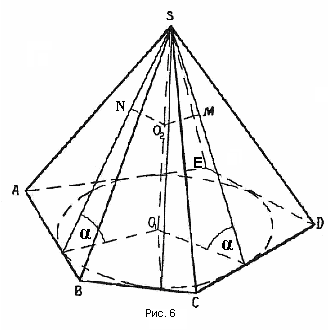
Теорема № 4. Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар.

Замечание. Это условие – достаточное и не является необходимым.

Доказательство

Докажем, что любая точка (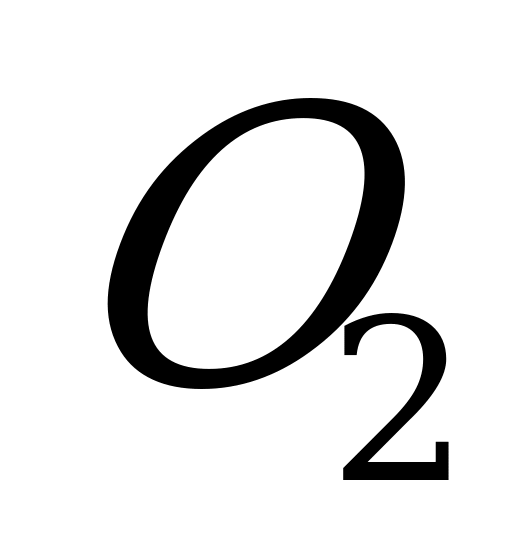 ) (рис.6) высоты такой пирамиды равноудалена от всех боковых граней. Плоскости линейных углов двугранных углов при основании перпендикулярны боковым граням (т.к. плоскость боковой грани проходит через ребро основания, которое перпендикулярно плоскости линейного угла), а потому, если мы опустим на боковые грани перпендикуляры 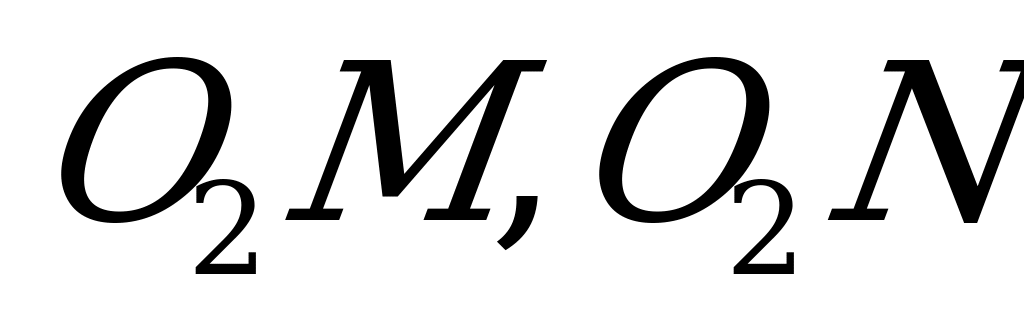и т.д., то они будут лежать в плоскостях линейных углов, а точки M, N и т.д. окажутся на высотах боковых граней, опущенных из вершины пирамиды.

(по гипотенузе и острому углу), а потому ОМ=ON=… , т.е. точка 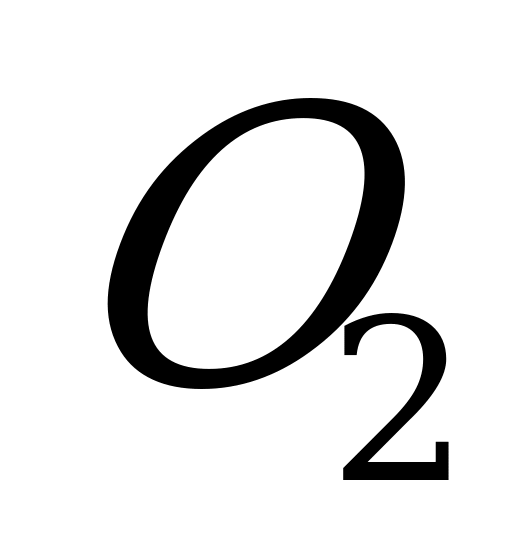равноудалена от всех боковых граней. Из этого следует, что центр шара, вписанного в такую пирамиду, лежит на высоте пирамиды. Точка пересечения высоты пирамиды с биссектрисой линейного угла двугранного угла при основании пирамиды, в плоскости которого расположена высота пирамиды, есть центр шара, вписанного в пирамиду, и притом единственного.

Следствие 1. Центр шара, вписанного в пирамиду, у которой боковые грани одинаково наклонены к основанию, лежит в точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного угла при основании пирамиды, стороной которого служит высота боковой грани, проведенная из вершины пирамиды.

Следствие 2. В правильную пирамиду можно вписать шар.

VI. Комбинация шара с усеченной пирамидой

1. Шар, описанный около правильной усеченной пирамиды

Теорема. Около усеченной пирамиды можно описать шар в том и только в том случае, если около ее оснований можно описать окружности, и прямая, проведенная через их центры, перпендикулярна плоскости основания (рис. 7).

Т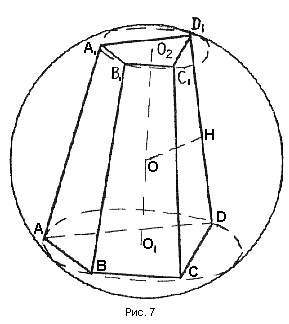 еорема 5. Около любой правильной усеченной пирамиды можно описать шар.

Замечание. Это условие является достаточным, но не является необходимым.

Доказательство

Известно, что около оснований правильной усеченной пирамиды можно описать окружности и что прямая, проходящая через центры этих окружностей, перпендикулярна основаниям. Следовательно, все точки, равноудаленные от вершины каждого основания (следствие из геометрического места точек № 4), лежат на этой прямой. Точка пересечения этой прямой с осью симметрии любого бокового ребра, лежащей в плоскости этой прямой и бокового ребра, есть центр шара, описанного около правильной усеченной пирамиды. Легко показать, что эта точка единственная.

Следующие теоремы без доказательства..

2. Шар, вписанный в правильную усеченную пирамиду

Теорема. В усеченную пирамиду можно вписать шар в том и только в том случае, если биссекторные плоскости всех двугранных углов при боковых ребрах пересекаются по одной прямой, а отрезок ее, отсеченный основаниями усеченной пирамиды, делится пополам биссекторной плоскостью любого двугранного угла при основании.

Т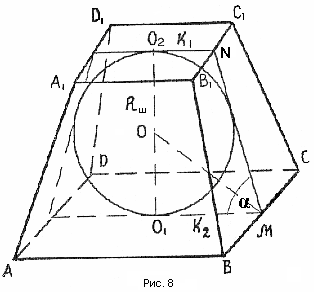 еорема 6. В правильную усеченную пирамиду можно вписать шар в том и только в том случае, если апофема пирамиды равна сумме апофем оснований (рис.8).

Центр шара есть точка пересечения высоты правильной усеченной пирамиды, проходящей через центр основания 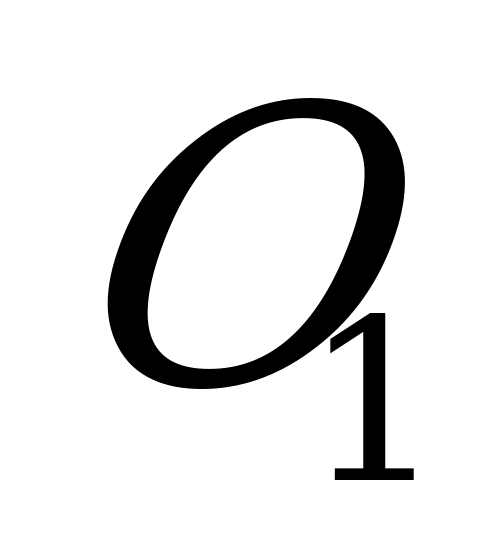и биссектрисы линейного угла двугранного угла при основании .

VII. Комбинация шара с круглыми телами

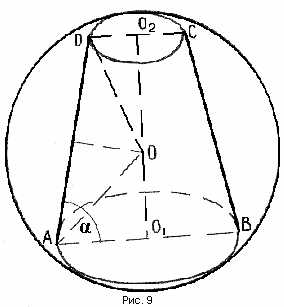
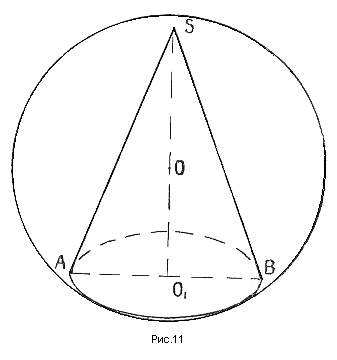
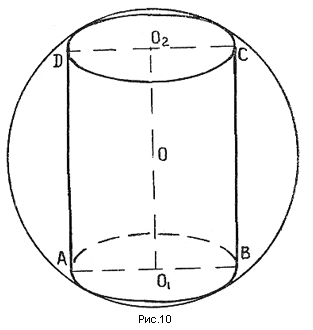
Теорема 7. Около цилиндра, усеченного конуса, конуса (прямых круговых), можно описать шар. (рис. №№ 9,10, 11).

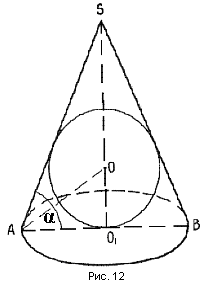
Теорема 8. В любой конус (прямой круговой) можно вписать шар (рис. № 12).

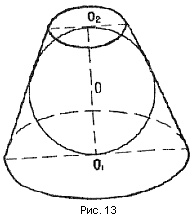
Теорема 9. В усеченный конус (прямой, круговой) можно вписать шар в том и только в том случае, если его образующая равна

сумме радиусов оснований (рис. № 13).

10