Компьютерное моделирование "Транспортная задача" (экономика)

Транспортная задача

Задача 1. Три склада должны обеспечить поставку компьютерных мониторов в четыре магазина. Объемы заявок магазинов и объемы поставок складами заданы (пример 15.3).

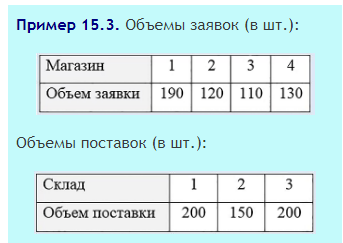
Транспортная компания, которая должна перевезти мониторы (штучный товар), рассчитала затраты на перевозку одного монитора по каждому маршруту и составила таблицу удельных затрат на перевозки (пример 15.4). Найти план перевозок с минимальной стоимостью.

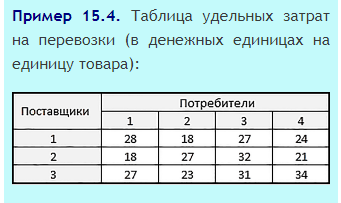
Исходные данные компьютерной модели разместим по схеме, приведенной в примере 15.6.

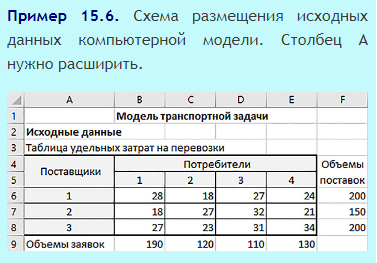
Расчетную таблицу будем строить по аналогичной схеме (пример 15.7).

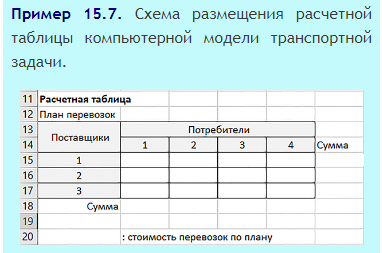
После ввода заголовков в ячейки A11 и A12 можно таблицу из раздела «Исходные данные» скопировать в раздел «Расчетная таблица» (пример 15.8). Пример 15.8. Для копирования таблицы из раздела «Исходные данные» следует выделить диапазон A4:E8 и скопировать его на диапазон A13:E17.

Начальные значения ячеек плана перевозок могут быть любыми числами, поэтому скопированные значения ячеек плана перевозок можно оставить.

В ячейку A18 вводится надпись «Сумма». В ячейку B18 вводится формула суммы значений ячеек этого столбца расчетной таблицы. Затем этой формулой надо заполнить диапазон C18:E18.

В ячейку F14 вводится надпись «Сумма». В ячейку F15 вводится формула суммы значений ячеек этой строки расчетной таблицы. Затем этой формулой заполняется диапазон F16:17.

В задаче необходимо найти такой план перевозок, для которого их суммарная стоимость минимальна в сравнении с другими планами.

Построим функцию V, которая вычисляет суммарную стоимость перевозок по заданному в модели плану.

Затраты на перевозку товара по одному маршруту «склад i — магазин j» будут равны произведению стоимости перевозки на ее объем. Стоимость перевозки задана в ячейке таблицы удельных затрат, а объем — в такой же ячейке таблицы плана перевозок.

Для построения функции V нужно перемножить значения соответствующих ячеек двух таблиц (диапазонов), а затем все произведения сложить. Введем формулу для вычисления функции V в ячейку А20 (пример 15.9). Пример 15.9. Для ввода значения функции V используем матема­тическую функцию СУММПРОИЗВ(), которая возвращает сумму произве­дений ячеек двух диапазонов (массивов).

Табличный курсор устанавливаем на ячейку A20, щелчком по кнопке Вставить функцию в строке формул, открываем окно Вставка функции. Проводим поиск функции по ее имени, затем дважды щелкаем по ее имени в списке. Открывается окно для ввода аргументов. В таблице выделяем диапазон B6:E8. Он записывается в поле аргумента Массив1. Затем в окне щелкаем по полю второго аргумента Массив2 и в таблице выделяем массив B15:E17. Щелчком по кнопке OK завершаем ввод.

Теперь следует вызвать окно Параметры поиска решения и ввести исходные данные для поиска решения.

Целевая функция V размещена в ячейке A20, критерий — Минимум, изменяя ячейки переменных диапазона B15:E17 (ячейки плана перевозок), переходим к вводу ограничений (пример 15.10). Пример 15.10. Нетрудно увидеть, что суммы в ячейках правее плана перевозок должны давать объемы поставок, которые заданы в правом столбце начальных данных. А суммы в ячейках ниже плана перевозок — объемы заявок, которые заданы в последней строке  начальных данных.

Такие ограничения Excel позволяет задавать как равенства диапазонов.

Щелкаем по кнопке Добавить. В новом окне для ввода ограничений в левое поле выделяем диапазон B18:E18. Во втором поле выбираем знак равенства. В третье поле вводим диапазон B9:E9. Щелкаем по кнопке OK.

Аналогично вводим условие равенства диапазонов F15:F17 и F6:F8.

Так как товар штучный, следует ячейки диапазона B15:E17 плана перевозок сделать целыми и неотрицательными (см. пример 14.11).

Под полем для ограничений должна стоять галочка выбора пункта Сделать переменные без ограничений неотрицательными.

После настроек в окне Параметры поиска решения щелкаем по кнопке Найти решение. 

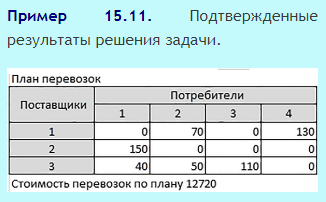
Задача 2. Решите транспортную задачу, уменьшив вдвое объемы заявок и объемы отгрузки в условиях задачи, рассмотренной в параграфе.

Задача 3. Решите следующую транспортную задачу. Компания владеет тремя заводами, которые производят штучную продукцию одного вида и имеют производительность 600, 300, 330 единиц продукции в год. Компания обязалась за год поставить в четыре города соответственно 350, 350, 230 и 300 единиц продукции. Таблица удельных стоимостей перевозки имеет вид:

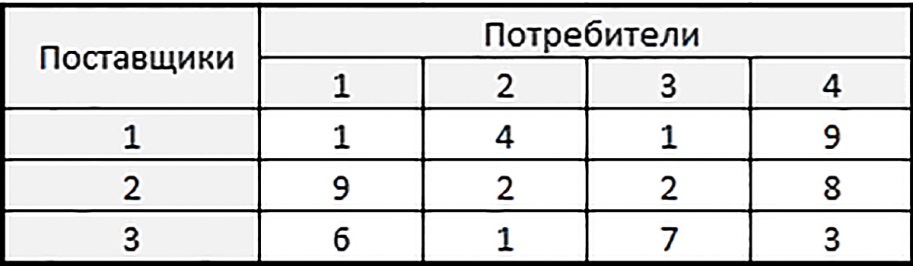
Задача 4. Решите транспортную задачу со следующими исходными данными для штучного товара.

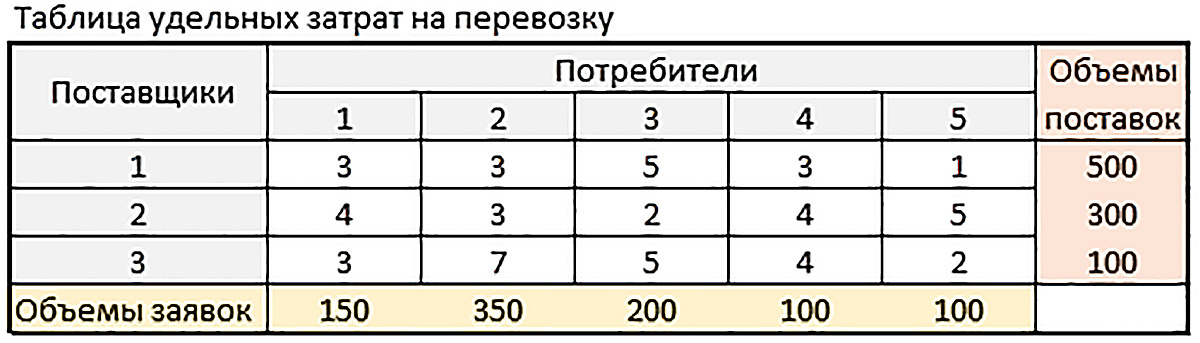
Задача 5. Решите транспортную задачу со следующими исходными данными для штучного товара.

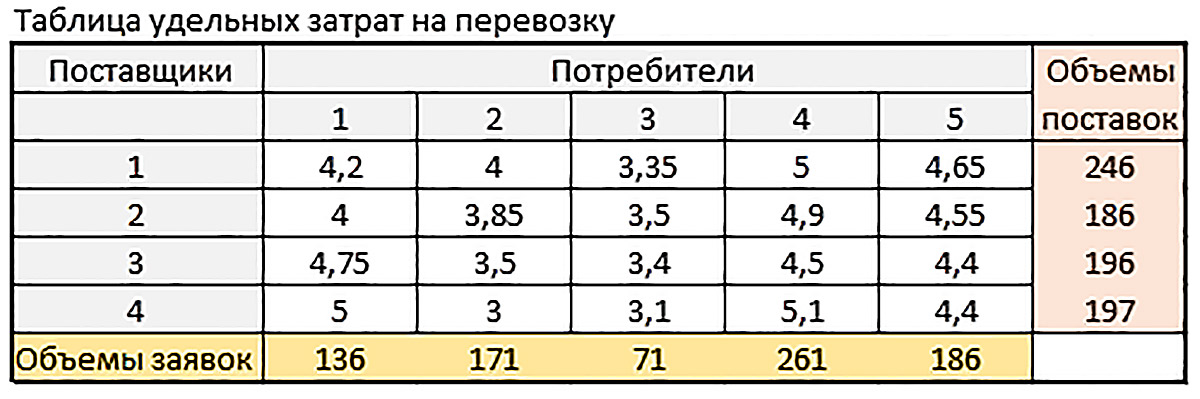
3