Комплексного числа

22.2. ФОРМЫ КОМПЛЕКСНОГО ЧИСЛА

Выражение

называется алгебраической формой комплексного числа.

1

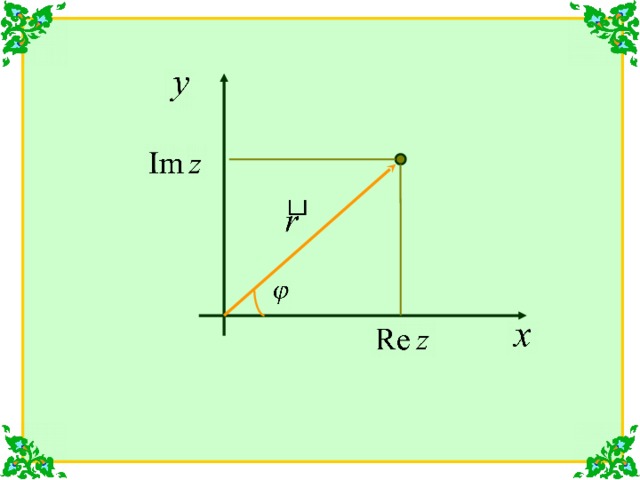
С каждой точкой комплексной плоскости связан радиус-вектор точки

Длина этого вектора называется модулем комплексного числа z и обозначается

Угол, образованный радиус-вектором точки и осью х называется аргументом комплексного числа z и обозначается

Из всех значений аргумента выделяется главное значение

удовлетворяющее условию

ПРИМЕР.

Поскольку

Из рисунка видно, что

Тогда

Выражение

называется тригонометрической формой комплексного числа.

2

Свойства арифметических операций над комплексными числами

1

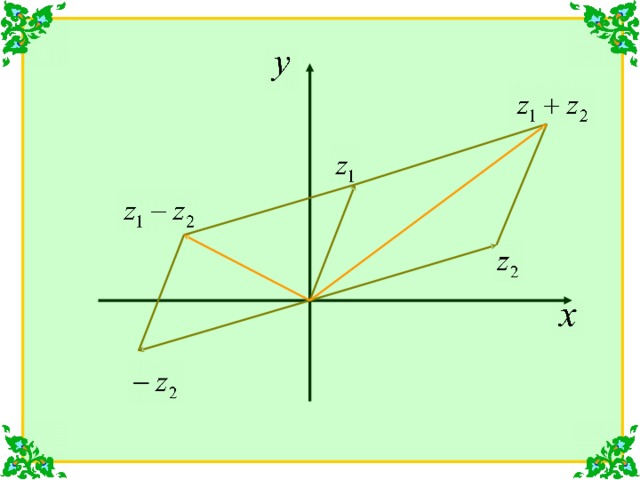
При сложении (вычитании) комплексных

чисел, их радиус-векторы складываются

(вычитаются) по правилу параллелограмма.

2

Модуль произведения (частного) двух

комплексных чисел равен произведению

(частному) модулей этих чисел, а аргумент

- сумме (разности) аргументов этих чисел.

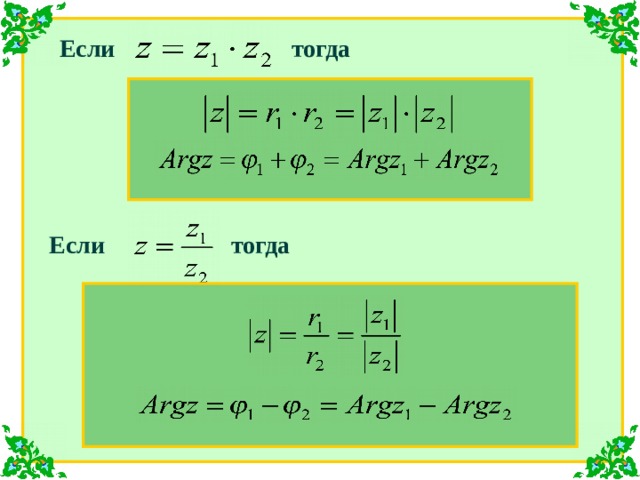
тогда

Если

Если

тогда

Геометрически умножение числа z 1 на число z 2 означает изменение длины радиус-вектора r 1 (или r 2 ) в r 2 (или в r 1 ) раз и его поворот вокруг точки щ против часовой стрелки на угол φ 2 (или φ 1 ).

ПРИМЕР.

Комплексные числа

представить в тригонометрической форме и найти их произведение и частное.

Решение.

Найдем модули этих комплексных чисел:

Теперь найдем аргументы этих комплексных чисел:

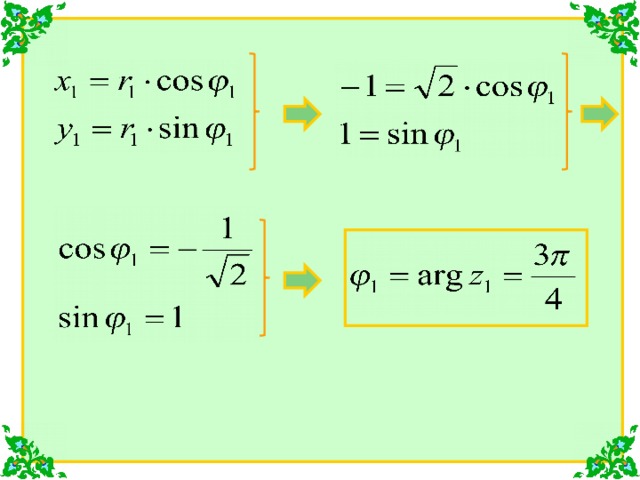
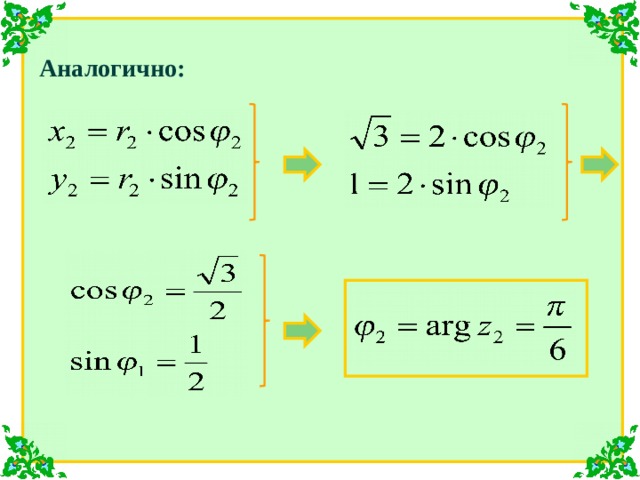
Аналогично:

Тогда в тригонометрической форме комплексные числа запишутся в виде:

Находим их произведение:

Находим их частное:

Т.к. при умножении комплексных чисел их модули перемножаются, а аргументы - складываются, то можно получить формулу возведения комплексного числа в натуральную степень.

формула Муавра

ПРИМЕР.

Вычислить

Решение.

Запишем это число в тригонометрической форме:

Рассмотрим операцию извлечения корня из комплексного числа. Пусть

тогда

следовательно

ПРИМЕР.

Вычислить

Решение.

Следовательно, получается три значения корня:

Изобразим эти точки на комплексной плоскости:

Точки будут равноудалены друг от друга на окружности с радиусом