ДЕПАРТАМЕНТ ЛЕСНОГО ХОЗЯЙСТВА НИЖЕГОРОДСКОЙ ОБЛАСТИ
Государственное бюджетное профессиональное
образовательное учреждение Нижегородской области
«КРАСНОБАКОВСКИЙ ЛЕСНОЙ КОЛЛЕДЖ»
КОМПЛЕКТ
КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ
ПО ДИСЦИПЛИНЕ ЕН.01 «МАТЕМАТИКА»
Специальность 35.02.01 «Лесное и лесопарковое хозяйство»
р.п. Красные Баки
2018 год
Одобрено на заседании предметно-цикловой комиссии
общеобразовательных дисциплин
Протокол №_______ от «_____» _________ 2018г.
Председатель ПЦК _____________ /Т.В. Поспелова /
Разработчики:
ГБПОУ НО «КБЛК» преподаватель Г.А.Чудоквасова
(место работы) (занимаемая должность) (инициалы, фамилия)
Общие положения
Контрольно-оценочные средства (КОС) предназначены для контроля и оценки образовательных достижений обучающихся, освоивших программу учебной дисциплины ЕН.01.Математика.
КОС включают контрольные материалы для проведения текущего контроля и промежуточной аттестации в форме дифференцированного зачета.
КОС разработаны на основании положений:
основной профессиональной образовательной программы по направлению подготовки специальности СПО 35.02.01 «Лесное и лесопарковое хозяйство»;
программы учебной дисциплины ЕН.01. «Математика».
2. Результаты освоения дисциплины, подлежащие проверке
| Результаты обучения (освоенные умения, усвоенные знания) | Основные показатели оценки результатов |
| У1. Умение решать обыкновенные дифференциальные уравнения | Решение дифференциальных уравнений первого и второго порядка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Вычисление предела функции в точке и в бесконечности Исследование функции на непрерывность в точке Нахождение производной функции Нахождение производных высших порядков Исследование функции и построение графика Нахождение неопределенных интегралов Вычисление определенных интегралов Нахождение частных производных |
| У3. Умение решать простейшие задачи, используя элементы теории вероятностей | Нахождение вероятности случайного события
|
| У4. Умение выполнять действия над векторами | Построение точек и нахождение их координат в прямоугольной декартовой и полярной системах координат Нахождение скалярного произведения векторов
|
| З1. Знание роли и места математики в современном мире, общности ее понятий и представлений | Знать роль математики при изучении спецпредметов, логичность математических понятий и теорем. |
| З2. Знание основ аналитической геометрии | Знать способы задания прямых на плоскости, их уравнения; кривые 2 порядка, их канонические уравнения. |
| З3. Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики | Перечисление последовательности действий при решении систем линейных уравнений методом обратной матрицы, по формулам Крамера, методом Гаусса. Формулировка определений и перечисление свойств скалярного произведения векторов. Классификация точек разрыва. Формулировка правил дифференцирования и перечисление производных основных элементарных функций. Перечисление табличных интегралов. Формулировка классического определения вероятности. |
| З4. Знание основных численных методов решения прикладных задач | Перечисление основных численных методов решения прикладных задач. |
| З5. Знание простых математических моделей систем и процессов в сфере профессиональной деятельности | Формулировка геометрического и механического смысла производной. Приложение определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения, пути, пройденного точкой. Описание процессов в естествознании и технике с помощью дифференциальных уравнений. |
3. Распределение оценивания результатов обучения по видам контроля
| Наименование элемента умений или знаний | Виды аттестации |
| Текущий контроль | Промежуточная аттестация |
| Умение решать обыкновенные дифференциальные уравнения
| устные ответы, защита практической работы №9;контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления
| устные ответы, защита практической работы №6,7,8;контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Умение решать простейшие задачи, используя элементы теории вероятностей | устные ответы, защита практической работы № 10;контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Умение выполнять действия над векторами | устные ответы, защита практической работы №2;контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Знание роли и места математики в современном мире, общности ее понятий и представлений | устные ответы, защита практических работ; контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Знание основ аналитической геометрии | устные ответы, контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики | устные ответы, защита практической работы №3,4,6,7,8,10;контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Знание основных численных методов решения прикладных задач | устные ответы, защита практической работы №5,9;контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
| Знание простых математических моделей систем и процессов в сфере профессиональной деятельности | устные ответы, защита практических работ; контроль выполнения самостоятельной работы по темам | Дифференцированный зачет |
4. Распределение типов контрольных заданий по элементам знаний и умений.
| Содержание учебного материала по программе УД | Тип контрольного задания |
| У1 | У2 | У3 | У4 | З1 | З2 | З3 | З4 | З5 |
| Раздел 1. Элементы линейной алгебры и аналитической геометрии |
|
|
|
|
| Тема 1.1.Матрицы и определители. Системы линейных уравнений. |
|
|
|
|
|
|
|
| расчетное задание6.1 |
| Тема 1.2. Векторы на плоскости и в пространстве, линейные операции с векторами. Скалярное произведение векторов. |
|
|
| устный ответ 6.2, расчетное задание6.3 |
|
|
|
| устный ответ 6.2 |
| Тема 1.3. Системы координат на плоскости и в пространстве. |
|
|
| расчетное задание6.3 |
|
|
|
|
|
| Тема 1.4. Уравнения прямых на плоскости. |
|
|
|
|
| устный ответ |
|
|
|
| Тема 1.5. Кривые второго порядка. |
|
|
|
|
| устный ответ |
|
|
|
| Раздел 2. Введение в анализ. Дифференциальное исчисление функций одной и двух переменных. |
|
|
|
|
| Тема 2.1. Функция одной переменной. |
| расчетное задание6.5 |
|
|
|
| расчетное задание6.5 |
|
|
| Тема 2.2. Предел и непрерывность функции. |
| расчетное задание6.4 |
|
|
|
|
|
|
|
| Тема 2.3. Производная и дифференциал функции. Производные высших порядков. |
| расчетное задание6.6 6.8 |
|
|
|
| расчетное задание6.6, устный ответ6.7 |
|
|
| Тема 2.4. Функции нескольких переменных. |
| расчетное задание 6.12 |
|
|
|
|
|
|
|
| Раздел 3. Интегральное исчисление функции одной переменной |
|
|
|
|
| Тема 3.1. Неопределенный интеграл и его свойства |
| расчетное задание 6.9 |
|
|
|
|
|
|
|
| Тема 3.2. Таблица основных формул интегрирования. Простейшие приемы интегрирования. |
|
|
|
|
|
| устный ответ 6.10 |
|
|
| Тема 3. 3. Определенный интеграл |
| расчетное задание 6.11 |
|
|
|
| расчетное задание 6.11 |
|
|
| Тема 3.4. Приложения определенного интеграла. |
| расчетное задание 6.11 |
|
|
|
| расчетное задание 6.11 |
|
|
| Раздел 4. Обыкновенные дифференциальные уравнения |
|
|
|
|
| Тема 4.1. Дифференциальные уравнения первого порядка с разделенными и разделяющимися переменными. | расчетное задание 6.13 |
|
|
|
|
|
| расчетное задание 6.13 |
|
| Тема 4.2. Линейные дифференциальные уравнения первого порядка. |
|
|
|
|
|
|
|
| устный ответ 6.14 |
| Тема 4.3. Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами | расчетное задание 6.13 |
|
|
|
|
|
|
|
|
| Тема 4.4. Дифференциальные уравнения второго порядка, допускающие понижение порядка. |
|
|
|
| устный ответ 6.14 |
|
| устный ответ 6.14 |
|
| Раздел 5. Элементы теории вероятностей и математической статистики |
|
|
|
|
| Тема 5.1. Основные понятия и теоремы теории вероятностей. Случайные величины. |
|
| расчетное задание 6.15 |
|
|
| расчетное задание 6.15 |
|
|
| Тема 5.2. Элементы математической статистики. |
|
| расчетное задание 6.15 |
|
|
|
|
|
|
5. Распределение типов и количества контрольных заданий по элементам знаний и умений, контролируемых на промежуточной аттестации.
| Содержание учебного материала по программе УД | Тип контрольного задания |
| У1 | У2 | У3 | У4 | З1 | З2 | З3 | З4 | З5 |
| Раздел 1. Элементы линейной алгебры и аналитической геометрии |
|
|
|
|
| Тема 1.1.Матрицы и определители. Системы линейных уравнений. |
|
|
|
| Задание№8, 9ДЗ | Задание№8, 9ДЗ |
|
| Задание№8, 9ДЗ |
| Раздел 2. Введение в анализ. Дифференциальное исчисление функций одной и двух переменных. |
|
|
|
|
| Тема 2.2. Предел и непрерывность функции. |
|
|
|
|
|
| Задание№6, 9ДЗ |
|
|
| Тема 2.3. Производная и дифференциал функции. Производные высших порядков. |
| Задание№3 ДЗ |
|
|
|
|
|
|
|
| Раздел 3. Интегральное исчисление функции одной переменной |
|
|
|
|
| Тема 3.2. Таблица основных формул интегрирования. Простейшие приемы интегрирования. |
| Задание№1,4 ДЗ |
|
| Задание№1,4 ДЗ |
|
|
|
|
| Тема 3.3. Определенный интеграл |
| Задание№2 ДЗ |
|
| Задание№2 ДЗ |
|
|
| Задание№2 ДЗ |
| Тема 3.4. Приложения определенного интеграла. |
| Задание№5 ДЗ |
|
| Задание№5 ДЗ |
|
|
| Задание№5 ДЗ |
| Раздел 4. Обыкновенные дифференциальные уравнения |
|
|
|
|
| Тема 4.1. Дифференциальные уравнения первого порядка с разделенными и разделяющимися переменными. | Задание№7 ДЗ |
|
|
|
|
|
| Задание№7 ДЗ |
|
6. Структура контрольного задания
6.1. Расчетное задание
6.1.1. Текст задания
Вариант 1
Найти матрицу C=A+3B, если 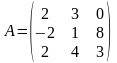 ,
,  .
.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант 2
Найти матрицу C=2A-B, если 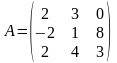 ,
,  .
.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант 3
Найти матрицу C=3A+B, если 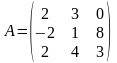 ,
,  .
.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант 4
Найти матрицу C=A-4B, если 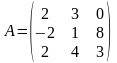 ,
,  .
.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант 5
Найти матрицу C=4A-B, если 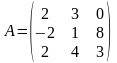 ,
,  .
.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

Вариант 6
Найти матрицу C=A+2B, если 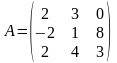 ,
,  .
.
Решить систему линейных уравнений по формулам Крамера.
Решить систему линейных уравнений методом Гаусса.

6.1.2. Время на выполнение: 60 мин.
6.1.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З5. Знание простых математических моделей систем и процессов в сфере профессиональной деятельности | Выполнение действий над матрицами, вычисление определителей. Решение систем линейных уравнений по формулам Крамера Перечисление последовательности действий при решении систем линейных уравнений по формулам Крамера, методом Гаусса | 4 балла |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.2. Устный ответ
6.2.1. Текст задания
Дать определение вектора.
Дать определение проекции вектора на ось и перечислить ее свойства.
Дать определение скалярного произведения векторов и перечислить его свойства.
Дать определение векторного произведения векторов и перечислить его свойства.
Дать определение смешанного произведения векторов и перечислить его свойства.
6.2.2. Время на выполнение: 20 мин.
6.2.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У4. Умение выполнять действия над векторами. З5. Знание простых математических моделей систем и процессов в сфере профессиональной деятельности | Формулировка определений и перечисление свойств скалярного, векторного и смешанного произведения векторов | 5 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.3. Расчетное задание
6.3.1. Текст задания
Вариант 1
Задание 1
(.) А (5; -3; 2) (.) B (2; 4; 1)
На прямой АВ найти (.) С делящую АВ в отношении 2:1
Задание 2
На оси OZ найти точку, равноудаленную от (.) А (2;4;3) (.)B (-3;5;1)
Задание 3
Найти длину  и его направляющие косинусы
и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов
 и
и 
Задание 5
При каких Р векторы 
 перпендикулярны.
перпендикулярны.
Вариант 2.
Задание 1
(.) А (3; 4; 5) (.) B (2; 1; 1)
На прямой АВ найти (.) Nделящую АВ в отношении 3:2
Задание 2
На оси OX найти точку, равноудаленную от (.) А (1;3;5) (.)B (-3;2;1)
Задание 3
Найти длину  и его направляющие косинусы
и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов
 и
и 
Задание 5
При какихM векторы 
 перпендикулярны
перпендикулярны
Вариант 3.
Задание 1
(.) А (5; 4; 3) (.) B (1; 1; 1)
На прямой АВ найти (.) Nделящую АВ в отношении л = 4
Задание 2
На оси OY найти точку, равноудаленную от (.) А (2;4;1) (.)B (-2;-4;3)
Задание 3
Найти длину  и его направляющие косинусы
и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов
 и
и 
Задание 5
При какихM векторы  перпендикулярны
перпендикулярны
Вариант 4.
Задание 1
(.) M (2; 2; -1) (.) M1 (3; 4; 1)
На прямой MM1 найти (.) PделящуюMM1 в отношении 4:1
Задание 2
На оси OY найти точку, равноудаленную от (.) А (2;6;3) (.)B (-3;-2;-1)
Задание 3
Найти длину  и его направляющие косинусы
и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов
 и
и 
Задание 5
При какихP векторы  перпендикулярны
перпендикулярны
Вариант 5.
Задание 1
(.) M (1; 1; 1) (.) M1 (-3; 5; -4)
На прямой MM1 найти (.) NделящуюMM1 в отношении 1:2
Задание 2
На оси OY найти точку, равноудаленную от (.) А (2;0;4) (.)B (4;3;6)
Задание 3
Найти длину  и его направляющие косинусы
и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов
 и
и 
Задание 5
При какихP векторы 
 перпендикулярны
перпендикулярны
Вариант 6.
Задание 1
(.) M (-2; -2; 4) (.) M1 (3; 2; 3)
На прямой MM1 найти (.) PделящуюMM1 в отношении 4:1
Задание 2
На оси OY найти точку, равноудаленную от (.) А (8;2;6) (.)B (-5;3;4)
Задание 3
Найти длину  и его направляющие косинусы
и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов
 и
и 
Задание 5
При какихP векторы перпендикулярны
Вариант 7.
Задание 1
(.) M (-1; -1; -1) (.) M1 (4; 4; 4)
На прямой AB найти (.) DделящуюAB в отношении 2:1
Задание 2
На оси OZ найти точку, равноудаленную от (.) А (-2;4;1) (.)B (5;6;1)
Задание 3
Найти длину  и его направляющие косинусы
и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов
 и
и 
Задание 5
При какихP векторы  перпендикулярны
перпендикулярны
Вариант 8
Задание 1
(.) М1 (2; 4; -2) (.) М2 (-2; 4; 2)
На прямой М1М2 найти (.) М, делящую ММ1 в отношении 1:3
Задание 2
На оси ОХ, найти (.) равноудаленную от (.) А (1; 4; 2) (.) B (-2; 4; -4)
Задание 3
Найти длину и его направляющие косинусы
Задание 4
Найти скалярное произведение векторов


Задание 5
Даны векторы
При каких р - векторы перпендикулярны
Задание 6
Найти (3a – 2b) · (5a – 6b), еслиa = 4; b = 6;  °
°
6.3.2. Время на выполнение: 70 мин.
6.3.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У4. Умение выполнять действия над векторами | Выполнение действий над векторами Построение точек и нахождение их координат в прямоугольной декартовой и полярной системах координат | 8 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.4. Расчетное задание
6.4.1. Текст задания
Вариант 1
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вариант 2
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вариант 3
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вариант 4
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вариант 5
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вариант 6
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
Вычислить предел функции:
.
6.4.2. Время на выполнение: 40 мин.
6.4.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Вычисление предела функции в точке и в бесконечности | 4 балла |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.5. Расчетное задание
6.5.1. Текст задания
Вариант 1
Исследовать функцию  на непрерывность в точке
на непрерывность в точке  .
.
Вариант 2
Исследовать функцию на непрерывность в точке  .
.
Вариант 3
Исследовать функцию  на непрерывность в точке
на непрерывность в точке  .
.
6.5.2. Время на выполнение: 10 мин.
6.5.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Исследование функции на непрерывность в точке | 1 балл |
| З3. Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики | Классификация точек разрыва |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.6. Расчетное задание
6.6.1. Текст задания
Вариант 1
Найти производную функции .
Найти производную третьего порядка функции  .
.
Написать уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  ,
,  .
.
Материальная точка движется по закону . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 2
Найти производную функции .
Найти производную третьего порядка функции  .
.
Написать уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  ,
,  .
.
Материальная точка движется по закону  . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 3
Найти производную функции .
Найти производную третьего порядка функции  .
.
Написать уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  ,
,  .
.
Материальная точка движется по закону  . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 4
Найти производную функции .
Найти производную третьего порядка функции  .
.
Написать уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  ,
,  .
.
Материальная точка движется по закону  . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 5
Найти производную функции  .
.
Найти производную третьего порядка функции  .
.
Написать уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  ,
,  .
.
Материальная точка движется по закону  . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
Вариант 6
Найти производную функции .
Найти производную третьего порядка функции  .
.
Написать уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой  ,
,  .
.
Материальная точка движется по закону  . Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
. Найти скорость и ускорение в момент времени t=5 с. (Перемещение измеряется в метрах.)
6.6.2. Время на выполнение: 40 мин.
6.6.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Нахождение производной функции. Нахождение производных высших порядков. | 4 балла |
| З3. Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики | Формулировка геометрического и механического смысла производной. |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.7. Устный ответ
6.7.1. Текст задания
Сформулировать правила дифференцирования и записать производные основных элементарных функций:
| 1о. | 
| 8о. | 
|
| 2о. |  В частности,      | 9о. | 
|
| 10о. | 
|
| 11о. | 
|
| 12о. | |
| 13о. | |
| ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ |
| 14о. | 
|
| 3о. | 
| 15о. | 
|
| 4о. |  В частности,  | 16о. | 
|
| 17о. | 
|
| 5о. |  В частности,   | 18о. |  В частности,  |
| 6о. | 
| ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ |
| 7о. | 
| 19о. | 
|
6.7.2. Время на выполнение: 15 мин.
6.7.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З3. Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики | Формулировка правил дифференцирования и перечисление производных основных элементарных функций | 28 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.8. Расчетное задание
6.8.1. Текст задания
Исследовать функцию и построить ее график.
Вариант 1
 .
.
Вариант 2
.
Вариант 3
 .
.
Вариант 4
.
Вариант 5
 .
.
Вариант 6
 .
.
Вариант 7
 .
.
Вариант 8
 .
.
6.8.2. Время на выполнение: 20 мин.
6.8.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Исследование функции и построение графика | 1 балл |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.9. Расчетное задание
6.9.1. Текст задания
Вариант 1
Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5).
.
.
.
.
 .
.
Найти неопределенные интегралы методом подстановки (для № 6-8).
 .
.
.
 .
.
Найти неопределенный интеграл методом интегрирования по частям: .
Вариант 2
Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5).
.
.
.
.
.
Найти неопределенные интегралы методом подстановки (для № 6-8).
 .
.
.
 .
.
Найти неопределенный интеграл методом интегрирования по частям: .
6.9.2. Время на выполнение: 60 мин.
6.9.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Нахождение неопределенных интегралов | 9 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.10. Устный ответ
6.10.1. Текст задания
Записать табличные интегралы:
1о. 
2о. 
В частности, 
3о. 
4о. 
В частности, 
5о. 
6о. 
7о. 
8о. 
9о. 
В частности, 
10о. 
В частности, 
6.10.2. Время на выполнение: 10 мин.
6.10.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З3. Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики | Перечисление табличных интегралов | 14 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.11. Расчетное задание
6.11.1. Текст задания
Вариант 1
Вычислить определенный интеграл: .
Вычислить определенный интеграл методом подстановки: .
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:  .
.
Скорость движения точки изменяется по закону  (м/с). Найти путь S, пройденный точкой за 10 с от начала движения.
(м/с). Найти путь S, пройденный точкой за 10 с от начала движения.
Вариант 2
Вычислить определенный интеграл: .
Вычислить определенный интеграл методом подстановки: .
Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями:  .
.
Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:  .
.
Скорость движения точки изменяется по закону  (м/с). Найти путь S, пройденный точкой за четвертую секунду.
(м/с). Найти путь S, пройденный точкой за четвертую секунду.
6.11.2. Время на выполнение: 40 мин.
6.11.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Вычисление определенных интегралов | 5 баллов |
| З3. Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики. З1. Знание роли и места математики в современном мире, общности ее понятий и представлений | Приложение определенного интеграла к вычислению площадей плоских фигур, объемов тел вращения, пути, пройденного точкой |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.12. Расчетное задание
6.12.1. Текст задания
Вариант 1
Найти частные производные функций.
 .
.
.
 .
.
Вариант 2
Найти частные производные функций.
 .
.
 .
.
 .
.
6.12.2. Время на выполнение: 25 мин.
6.12.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У2. Умение решать прикладные задачи с использованием элементов дифференциального и интегрального исчисления | Нахождение частных производных | 3 балла |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.13. Расчетное задание
6.13.1. Текст задания
Вариант 1
Являются ли данные функции решениями данных дифференциальных уравнений (для № 1-4).
.
.
 .
.
 .
.
Решить задачу Коши: .
Решить следующие дифференциальные уравнения первого и второго порядка (для № 6-12).
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
Вариант 2
Являются ли данные функции решениями данных дифференциальных уравнений (для № 1-4).
.
.
.
 .
.
Решить задачу Коши: .
Решить следующие дифференциальные уравнения первого и второго порядка (для № 6-12).
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.
6.13.2. Время на выполнение: 80 мин.
6.13.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У1. Умение решать обыкновенные дифференциальные уравнения | Решение дифференциальных уравнений первого и второго порядка | 12 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.14. Устный ответ
6.14.1. Текст задания
Сформулировать общие положения при составлении дифференциального уравнения по условию задачи.
Записать дифференциальное уравнение показательного роста и показательного убывания и получить его решение. Привести примеры прикладных задач, решаемых с его помощью.
Сформулировать задачу о радиоактивном распаде, записать для нее дифференциальное уравнение.
Сформулировать задачу о гармонических колебаниях, записать дифференциальное уравнение гармонических колебаний.
Сформулировать задачу о падении тел в атмосферной среде, записать для нее дифференциальное уравнение.
6.14.2. Время на выполнение: 30 мин.
6.14.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| З5. Знание простых математических моделей систем и процессов в сфере профессиональной деятельности | Описание процессов в естествознании и технике с помощью дифференциальных уравнений | 5 баллов |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
6.15. Расчетное задание
6.15.1. Текст задания
Из корзины, в которой находятся 4 белых и 7 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Определить вероятность появления «герба» при бросании монеты.
В корзине 20 шаров: 5 синих, 4 красных, остальные черные. Выбирают наудачу один шар. Определить, с какой вероятностью он будет цветным.
Событие А состоит в том, что станок в течение часа потребует внимания рабочего. Вероятность этого события составляет 0,7. Определить, с какой вероятностью станок не потребует внимания.
В одной корзине находятся 4 белых и 8 черных шаров, в другой – 3 белых и 9 черных. Из каждой корзины вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Бросают две монеты. Определить, с какой вероятностью появится «герб» на обеих монетах.
В лотерее 100 билетов. Разыгрывается один выигрыш в 200 рублей и двадцать выигрышей по 50 рублей. Пусть Х – величина возможного выигрыша для человека, имеющего один билет. Составить закон распределения этой случайной величины Х.
Случайная величина Х задана законом распределения:
Найти ее математическое ожидание.
Согласно статистике, вероятность того, что двадцатипятилетний человек проживет еще год, равно 0,992. Компания предлагает застраховать жизнь на год на 1000 у.е. с уплатой 10 у.е. взноса. Определить, какую прибыль ожидает компания от страховки одного двадцатипятилетнего человека.
Случайная величина Х задана законом распределения:
Найти дисперсию и среднее квадратичное отклонение этой случайной величины Х.
Случайные величины X и Y заданы законом распределения. Найти математическое ожидание этих случайных величин и определить по таблицам, какая из данных величин более рассеяна. Подсчитать дисперсии D(X) и D(Y). Убедиться, что D(X)D(Y).
6.15.2. Время на выполнение: 45 мин.
6.15.3. Перечень объектов контроля и оценки
| Наименование объектов контроля и оценки | Основные показатели оценки результата | Оценка |
| У3. Умение решать простейшие задачи, используя элементы теории вероятностей | Нахождение вероятности случайного события Составление закона распределения случайной величины Вычисление числовых характеристик случайных величин | 11 баллов |
| З3. Знание основных понятий и методов математического анализа, теории вероятностей и математической статистики | Формулировка классического определения вероятности |
За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл.
За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов.
7. Задания промежуточной аттестации.
К сдаче дифференцированного зачета допускаются студенты, сдавшие на положительную оценку все практические работы по изучаемой дисциплине.
Материалы для проведения промежуточной аттестации
Форма контроля: дифференцированный зачет
Семестр: 1
Группа: 21 ЛЛХ
Вариант 1
Найти интегралы: а) ; б) ;
в)
Вычислить интеграл: .
Найти одну из первообразных функции:  .
.
Для функции  найдите первообразную, график которой проходит через точку М (1 ; 2).
найдите первообразную, график которой проходит через точку М (1 ; 2).
Найдите площадь фигуры, ограниченной осью Ох и параболой  .
.
Вычислить пределы: а) ; б) ;
в) .
Решить дифференциальное уравнение: а) ; б)  .
.
8. Даны матрицы . Найти: А + В.
Вычислить определитель 3-го порядка:
Роспись преподавателя ________________/__________________/
подпись расшифровка
Вариант 2.
1. Найти интегралы: а) ; б)
в)
2. Вычислить интеграл:
3. Найти одну из первообразных функции:
4. Для функции найдите первообразную, график которой проходит через точку М(-1; 3).
найдите первообразную, график которой проходит через точку М(-1; 3).
5. Найдите площадь фигуры, ограниченной осью Ох и параболой 
6. Вычислить пределы: а)
б) в)
7. Решить дифференциальное уравнение: а) ; б)  .
.
8. Даны матрицы . Найти: А - В.
9. Вычислить определитель 3-го порядка:
Роспись преподавателя ________________/__________________/
подпись расшифровка
Для получения отметки «3» (удовлетворительно) обучающийся должен правильно выполнить любые пять заданий.
Отметка «4» (хорошо) выставляется при выполнении любых семи заданий. Отметка «5» (отлично) ставится за девять верно выполненных заданий.
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
1. Дадаян А.А. Математика: учебник/А.А.Дадаян.-3-е изд.- М.:ФОРУМ:ИНФРА-М,2013 Дополнительные источники:
1. Башмаков М.И. Математика: алгебра и начала математического анализа, геометрия, 2017 (Электронный ресурс) http://www/academiamoscow.ru/- ЭБС ООО ОИЦ «Академия»
2. Лисичкин В.Т., Соловейчик И.Л. Математика в задачах с решениями: Учебное пособие.-5-е изд., стер. - СПб.: Издательство «Лань»,2014.
3. Шипачев В.С. Математика: учебник и практикум для СПО/В.С. Шипачев: под ред. А.Н.Тихонова.-8-е изд.,перераб. И доп.-М.:Издательство Юрайт, 2016.-447 с.







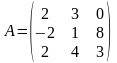 ,
,  .
.





 и его направляющие косинусы
и его направляющие косинусы и
и 

 перпендикулярны.
перпендикулярны. и его направляющие косинусы
и его направляющие косинусы и
и 









