
Комплект практических работ по математике
5 класс,
к Рабочей программе учебного курса «Математика» (5 класс)
основного общего образования (базовый уровень)
составлен учителем математики
Белорецкой компьютерной школы
Лукмановой Г.Х.
Практическая работа №1 (на клетчатой бумаге) «Построение узора из окружностей»
Практическая работа №1. (на клетчатой бумаге) «Построение узора из окружностей» (в 4 вариантах)
Практическая работа «Элементы окружности»
Практическая работа №2 «Построение углов»
Практическая работа №3 «Построение прямоугольника с заданными сторонами на нелинованной бумаге».
Практическая работа №4 «Площадь поверхности прямоугольного параллелепипеда.
Практическая работа №1 (на клетчатой бумаге) «Построение узора из окружностей»
Цели работы:
-
Знакомство с геометрическими фигурами - окружность и круг.
-
Изучение элементов окружности.
-
Измерение радиусов окружности и круга.
-
Построение окружности и круга.
-
Построение узора из окружностей.
Оборудование: циркуль, линейка, карандаш.
Ход работы
П ознакомьтесь с алгоритмомпостроения окружности и изучите ее свойства.
ознакомьтесь с алгоритмомпостроения окружности и изучите ее свойства.
-
Поставьте на листе тетради точку. Обозначь ее буквой О.
-
Возьмите циркуль в руки следующим образом: ножку циркуля с иглой установи в точку О, а ножку циркуля с грифелем вращайте вокруг данной точки, касаясь листа тетради. Циркуль опишет замкнутую линию. Ее называют окружностью. Точку О называют центром окружности.
-
Отметьте точку А на окружности и проведите отрезок, соединяющий точку А и центр окружности точку - О, такой отрезок называется радиус.
-
Постройте радиус ОВ.
| № | Радиус (обозначение отрезка) | Длина |
-
| ОА |
|
-
| ОВ |
|
Ответьте на вопросы и выполните задание:
-
Сколько радиусов можно провести в одной окружности?
-
Сравнитедлины этих отрезков.
-
Сделайте вывод, запишитеего в тетрадь.
-
Постройте отрезок МК, соединяющий две точки окружности, который проходит через её центр, такой отрезок называется диаметр.
-
Построй диаметр РТ.
| № | Диаметр (обозначение отрезка) | Длина |
-
| МК |
|
-
| РТ |
|
Ответьте на вопросы и выполните задание:
-
Сколько диаметров можно провести в одной окружности?
-
С равните длину диаметра с длиной радиуса.
равните длину диаметра с длиной радиуса.
-
Сделайте вывод.
-
Запишите вывод в тетрадь.
-
Нарисуйте окружность. Не меняя радиуса, переставьте ножку циркуля с иглой в любую точку на окружности и снова нарисуйте окружность. Точки пересечения этих окружностей станут центрами новых окружностей. Внутри основного круга появился цветок.
Контрольный вопрос:
Что можно сказать о расположении точек окружности по отношению к центру окружности?
Дополнительные вопросы и задания:
-
Нарисуйте две окружности, которые не пересекаются. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь.
-
Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите вывод в тетрадь.
-
Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов, расстояние между их центрами и сделай вывод. Запишите в тетрадь.
-
Приведите примеры окружности и круга в окружающих вас предметах.
Практическая работа (на клетчатой бумаге) «Построение узора из окружности»
Цель работы:1.Систематизировать знания по этой теме, выработать практические навыки работы с циркулем при построении окружности.
2.Развивать логическое мышление, интерес к предмету, способствовать формированию ключевых понятий, выполнение заданий творческого характера.
3. Воспитывать внимательность, аккуратность, умение четко организовывать самостоятельную и индивидуальную работу.
Оборудование: клетчатая бумага, карандаш, цветные карандаши, линейка, циркуль, ластик.
Ход работы.
Вариант№1
Практическое задание №1: нарисовать узоры с помощью циркуля
-
Начертите окружность радиусом 2см
-
Отметьте на окружности точку
-
Не меняя раствора циркуля, проведите из этой точки как из центра новую окружность
-
Она пересечет прежнюю окружность в двух точках.
-
Из этих точек как из центра, снова проведите окружности того же радиуса
-
Продолжив построение, вы получите нужную фигуру
-
Раскрасьте цветными карандашами увиденный вами узор.
Задание №2
1.Какая фигура называется окружностью?
2. Что называется радиусом?
3. Во сколько раз диаметр больше радиуса?
4. Выполните задание:
а) Отметьте точку С. Проведите окружность радиусом 3 см с центром в точке С.
б)Проведите диаметр окружности и обозначьте его.
в) Отметьте на окружности точку М. Проведите окружность с центром в точке М, проходящую через точку С. Запишите, чему равен ее радиус.
Контрольный вопрос: Сколько диаметров можно провести через центр окружности?
О
тветы: Практическое задание №1:

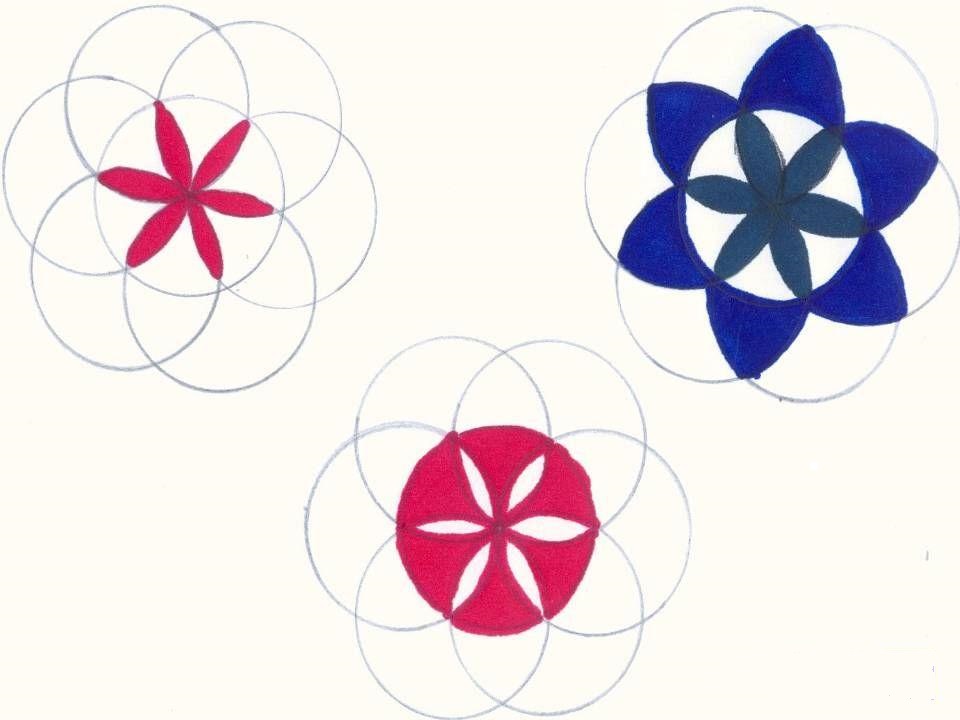
Задание №2:
-
Окружностью называется замкнутая линия, все точки которой лежат на одном и том же расстоянии от одной точки (центра окружности).
-
Радиусом называется отрезок, который соединяет центр окружности с точкой, лежащей на окружности.
-
В два раза.
-

Контрольный вопрос: бесконечно много.
Практическая работа (на клетчатой бумаге) «Построение узора из окружности»
Цель работы:1.Систематизировать знания по этой теме, выработать практические навыки работы с циркулем при построении окружности.
2.Развивать логическое мышление, интерес к предмету, способствовать формированию ключевых понятий, выполнение заданий творческого характера.
3. Воспитывать внимательность, аккуратность, умение четко организовывать самостоятельную и индивидуальную работу.
Оборудование: клетчатая бумага, карандаш, цветные карандаши, линейка, циркуль, ластик.
Ход работы.
Вариант№2
Практическое задание №1: нарисовать узоры с помощью циркуля
1.Начертите окружность радиусом 3см
2.Отметьте на окружности точку
3.Не меняя раствора циркуля, проведите из этой точки как из центра новую окружность
4.Она пересечет прежнюю окружность в двух точках.
5.Из этих точек как из центра, снова проведите окружности того же радиуса
6.Продолжив построение, вы получите нужную фигуру
7. Раскрасьте цветными карандашами увиденный вами узор.
Задание №2
1.Какая фигура называется кругом?
2. Что называется диаметром?
3. Во сколько раз радиус меньше диаметра?
4. Выполните задание:
а) Отметьте точки А и В. Проведите окружность с центром в точке А, проходящую через точку В.
б) Проведите диаметр окружности и обозначьте его.
в) Проведите окружность с центром в точке В радиусом 2 см. Запишите, чему равен ее диаметр.
Контрольный вопрос: Сколько окружностей проходит через три заданные точки, принадлежащие одной прямой?
Ответы:
Практическое задание №1:

Задание №2:
-
Кругом называется геометрическая фигура, которая ограничена окружностью.
-
Диаметром называется отрезок, который соединяет две точки окружности, проходящий через ее центр.
-
В два раза.
-

Контрольный вопрос: ни одной.
Практическая работа (на клетчатой бумаге) «Построение узора из окружности»
Цель работы:1.Систематизировать знания по этой теме, выработать практические навыки работы с циркулем при построении окружности.
2.Развивать логическое мышление, интерес к предмету, способствовать формированию ключевых понятий, выполнение заданий творческого характера.
3. Воспитывать внимательность, аккуратность, умение четко организовывать самостоятельную и индивидуальную работу.
Оборудование: клетчатая бумага, карандаш, цветные карандаши, линейка, циркуль, ластик.
Ход работы.
Вариант№3
Практическое задание №1: нарисовать узоры с помощью циркуля
1.Начертите окружность радиусом 2см 5 мм.
2.Отметьте на окружности точку
3.Не меняя раствора циркуля, проведите из этой точки как из центра новую окружность
4.Она пересечет прежнюю окружность в двух точках.
5.Из этих точек как из центра, снова проведите окружности того же радиуса
6.Продолжив построение, вы получите нужную фигуру
7. Раскрасьте цветными карандашами, увиденный вами узор.
Задание №2
1.Что называется окружностью?
2. Как называется отрезок, соединяющий две точки окружности и проходящий через центр?
3. Сколько радиусов помещается в диаметре?
4. Выполните задание:
а) Отметьте точки Аи С. Проведите окружность радиусом 2 см с центром в точке А.
б)Постройте окружность с центром в точкеС, пересекающую первую окружность.
в)Измерьте расстояние между центрами получившихся окружностей.
Контрольный вопрос: Сколько окружностей проходит через две заданные точки?
Ответы:
Практическое задание №1:

Задание №2:
-
Окружностью называется замкнутая линия, все точки которой лежат на одном и том же расстоянии от одной точки (центра окружности).
-
Диаметр.
-
Два.
-

Контрольный вопрос: бесконечно много.
Практическая работа (на клетчатой бумаге) «Построение узора из окружности»
Цель работы:1.Систематизировать знания по этой теме, выработать практические навыки работы с циркулем при построении окружности.
2.Развивать логическое мышление, интерес к предмету, способствовать формированию ключевых понятий, выполнение заданий творческого характера.
3. Воспитывать внимательность, аккуратность, умение четко организовывать самостоятельную и индивидуальную работу.
Оборудование: клетчатая бумага, карандаш, цветные карандаши, линейка, циркуль, ластик.
Ход работы.
Вариант№4
Практическое задание №1: нарисовать узоры с помощью циркуля
1.Начертите окружность радиусом 3см5 мм.
2.Отметьте на окружности точку
3.Не меняя раствора циркуля, проведите из этой точки как из центра новую окружность
4.Она пересечет прежнюю окружность в двух точках.
5.Из этих точек как из центра, снова проведите окружности того же радиуса
6.Продолжив построение, вы получите нужную фигуру
7. Раскрасьте цветными карандашами увиденный вами узор.
Задание №2
1.Что называется кругом?
2.Как называется отрезок, соединяющий центр окружности с любой точкой окружности?
3.Сколько надо взять радиусов, чтобы получился диаметр?
4. Выполните задание:
а) Постройте окружность с центром в точке О. Отметьте точку А, лежащую внутри окружности и точку В вне окружности.
б) Измерьте длину отрезков ОА и ОВ.
в) Сравните длину отрезков ОА И ОВ с радиусом окружности..
Контрольный вопрос: Сколько радиусов можно провести в окружности?
Ответы:
Практическое задание №1:

Задание №2:
-
Кругом называется геометрическая фигура, которая ограничена окружностью.
-
Радиус.
-
Два.
-

Контрольный вопрос: бесконечно много.
Практическая работа «Элементы окружности»
Задание 1. Постройте синим цветом круг радиусом 2см, а красным цветом окружность радиусом 1,5 см. В чём отличие круга и окружности: _____________________________________________________
_______________________________________________________________________________________
Задание 2. Запиши в таблицу обозначение элементов, изображённых на рисунке:
| 
| Диаметр |
|
| Хорда |
|
| Радиус |
|
| Дуга |
|
Задание 3. По рисунку определить, чем являются данные элементы: радиусом, диаметром, хордой или дугой. Данные слова вписать в клеточки напротив отрезков.
| 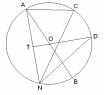
| АВ - |
| AC - |
|
| ОА - |
| OD - |
|
| NC - |
| ND - |
|
| OB - |
| DB- |
|
| AN- |
| СD - |
|
Задание 4. Вычислите площадь круга и длину окружности из задания 1.
1) _____________________________________________________________________________________
2) _____________________________________________________________________________________
Ответ: _________________________________________________________________________________
Задание 5.Закончите предложения:
1.Окружность — это угол в _____________ .
2. Наибольшая из хорд окружности–это _________________________.
3.Прямая, имеющая с окружностью одну общую точку, называется ________________.
4. Отрезок, соединяющий две точки окружности, называется __________________.
5.Геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки, называется _____________________________.
Практическая работа «Построение углов»
Цели работы:
-
Познакомиться с алгоритмом построения угла заданной градусной меры.
-
Научиться строить угол заданной градусной меры.
-
Научиться определять вид угла.
Оборудование: транспортир, линейка, карандаш.
Ход работы
П ознакомьтесь с алгоритмомпостроенияугол с помощью транспортира.
ознакомьтесь с алгоритмомпостроенияугол с помощью транспортира.
-
Отметьте вершину угла точку - О.
-
Постройте луч с началом в точке О.
-
Совместите вершину угла с центром транспортира.
-
Расположите транспортир так, чтобы построенная сторона угла проходила через начало отсчета на шкале транспортира (совместите с 00).
-
Найди на шкале транспортира деление, соответствующее данной градусной мере, сделайте метку карандашом.
-
Постройте луч с началом в точке О, проходящий через метку.
-
Проверьте, соответствует ли градусная построенного угола его виду (острый, прямой, тупой, развернутый).
-
Выполните построение заданных углов и заполните таблицу.
| Угол | Градусная мера угла | Вид угла |
| АОВ | 650 |
|
| МРК | 1250 |
|
| CDF | 900 |
|
Дополнительные вопросы и задания:
При помощи линейки и чертежного угольника с углами 300, 600, 900 и углами 450, 450, 900 можно построить любой угол, кратный 150.


Схемы построения углов

Выполните задание:
постройте с помощь чертежных треугольников угол, равный 1650.
Практическая работа №3 «Построение прямоугольника с заданными сторонами на нелинованной бумаге»
Цель работы:
-
Познакомиться с алгоритмом построения прямоугольника с заданными сторонами на нелинованной бумаге.
-
Научиться строить прямоугольник с заданными сторонами на нелинованной бумаге.
Оборудование:чертёжный угольник, линейка, карандаш.
Ход работы
Познакомьтесьс алгоритмом построения прямоугольника с заданными сторонами на нелинованной бумаге.

-
Выполните построение прямоугольника ABCDс указанными длинами сторон и проведите в нем диагонали, заполните таблицу.
| Длина стороны, a см | Длина стороны, b см | Длина диагонали AD | Длина диагонали BC |
| 4 | 5 |
|
|
Контрольный вопрос:
Сравните длины диагоналей, сделайте вывод, запишите его в тетрадь.
Дополнительное задание:
Вычислите периметр и площадь получившегося прямоугольника.
Практическая работа№ 3
“Построение прямоугольника с заданными сторонами
на нелинованной бумаге”
Цель работы: Научиться строить прямоугольники, используя чертёжные инструменты, по заданным длинам сторон. Находитьпериметр прямоугольников, в том числе выполняя необходимые измерения. Исследовать свойства прямоугольников путём эксперимента, наблюдения, измерения.
Оборудование: линейка, чертёжный угольник, карандаш, нелинованная бумага, транспортир.
Ход работы
1. Практическая часть
Для построения прямоугольника можно воспользоваться чертёжным треугольником.
Познакомьтесь с алгоритмом построения прямоугольника с заданными сторонами на нелинованной бумаге.
| Этапы построения | Описание построения | Образец построения |
| Шаг 1 | Начертим прямой угол А с помощью чертёжного треугольника. | 


 
А |
| Шаг 2 | На одной стороне угла с помощью линейки отложим отрезок АВ (например, равный 2 см), а на другой стороне отрезок AD (например, равный 4 см).
| 
В 

  
АD |
| Шаг 3 | Одну из сторон угольника приложим к лучу АВ так, чтобы вершина прямого угла совпала с точкой В. Проведём карандашом вдоль второй стороны угольника луч с началом в точке В. Получили второй прямой угол. | 
В   
  
АD |
| Шаг 4 | От точки В отложим отрезок BC, равный отрезку AD. Соединим точки C и D. |
 С С          A D A D |
По заданному алгоритму выполните построение прямоугольникаABCD со сторонами АВ = 4 см 5 мм и AD = 6 см
2. Ответьте на вопросы и выполните задания.
-
Получился ли прямоугольник? Как проверить? ________________________________________
2) Вставьте пропущенное слово: «Четырёхугольник, у которого все углы прямые, называют _________________________________».
3) В построенном прямоугольнике проведите диагонали.Измерьте их длины и запишите результат измерения: АС = _____, BD = _____.
4) Обозначьте точку пересечения диагоналей буквой О. Измерьте и запишите чему равны длины отрезков АО=_____, ВО=____, СО=____, OD=_____
3. Контрольный вопрос: Что можно сказать о длинах диагоналей?О точке пересечения диагоналей?
Сделайте вывод: «Диагонали прямоугольника ______________________.
Диагонали точкой пересечения делятся _____________________»
4. Дополнительные вопросы и задания:
-
Выпишите равные стороны прямоугольника.
_________________________________________________
2) Измерьте острый угол между диагоналями ____________
3) Вычислите периметр и площадь получившегося прямоугольника.
Р=_____________________________________________________________
S=_____________________________________________________________
4) С помощью, каких инструментов можно построить прямоугольник на нелинованной бумаге? ________________________________________
5) Где в нашей жизни могут пригодиться умения производить построения прямоугольника или квадрата на нелинованной бумаге?
_______________________________________________________________
_______________________________________________________________
Оценивание работы
| № задания | 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 5 |
| баллы | 2 | 1 | 1 | 1 | 1 | 2 | 1 | 1 | 2 | 1 | 1 |
6-9 баллов - оценка «3»
10-12 баллов - оценка «4»
13-14 баллов - оценка «5»
Практическая работа №4 «Площадь поверхности прямоугольного параллелепипеда»
Цель работы:
-
Познакомиться с алгоритмом измерения длины, ширины и высоты куба и прямоугольного параллелепипеда.
-
Научиться вычислятьплощадь поверхности куба и площадь поверхности прямоугольного параллелепипеда.
Оборудование: прямоугольные параллелепипеды, кубики, линейка.д работы
-
И змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).
змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).
-
Вычислите площадь полной поверхности прямоугольного параллелепипеда.
S=2(ab + bc + ac)
-
Вычислите площадь полной поверхности куба.
S=6a2
-
Сделайте вычисления.
-
Перенесите таблицу в тетрадь и заполните её.
| Геометрическая фигура | Длина, aсм | Ширина, b см | Высота, c см | Площадь поверхности, S см2 |
| Прямоугольный параллелепипед |
|
|
|
|
| Куб |
|
|
|
|
Контрольные вопросы:
-
Что можно сказать о противоположных гранях прямоугольного параллелепипеда? Сделайте вывод, запишите его в тетрадь.
-
Что можно сказать о гранях куба? Сделайте вывод, запишите его в тетрадь.
Дополнительные вопросы и задания:
1. Выразите:
а) в кубических дециметрах: 5 м3 680 см3; 7 м3 15 см3;
б) в кубических сантиметрах: 4 дм3 536 см3; 2 дм3 80 см3.
2. Сколько кубиков с ребром 10 см необходимо взять, чтобы построить башню длиной 25 м, шириной 6 м и высотой 100 м?
Ф.И. _______________________________________ класс_______
Практическая работа №4 по теме
“Площадь поверхности куба и прямоугольного параллелепипеда”
Вариант 1.
Цель работы:
-
Познакомиться с алгоритмом измерения длины, ширины и высоты куба и прямоугольного параллелепипеда.
-
Научиться вычислять площадь поверхности куба и прямоугольного параллелепипеда.
Оборудование: прямоугольные параллелепипеды (модели, или предметы, имеющие форму прямоугольного параллелепипеда), линейки.
Ход работы.
Работа в парах.
-
И змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
| Длина а см | Ширина bсм | Высота c см | Площадь поверхности Sсм2 |
|
|
|
|
|
-
Вычислите площадь полной поверхности прямоугольного параллелепипеда.
S= 2(ab+bc+ac).

Ответ внесите в таблицу.
Индивидуальная работа.
-
Н
 а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки
1 см × 1 см изображен куб. Найдите длину ребра куба. Результат запишите в таблицу.
а
| Длина ребра а см | Площадь одной грани а2 см2 | Количество граней куба | Площадь поверхности куба Sсм2 |
|
|
|
|
|
-
Вычислите площадь одной грани куба. S=а2.Результат занесите в таблицу.
-
Впишите число граней куба в таблицу.
-
В ычислите площадь поверхности куба.
ычислите площадь поверхности куба.
Ответ внесите в таблицу.
Контрольные вопросы.
-
Что можно сказать про все грани куба? Сделайте вывод и запишите его.
-
Что можно сказать про грани прямоугольного параллелепипеда? Сделайте вывод и запишите его.

Дополнительные задания.
-
Выразите в метрах: 32 м 50 см; 140 м 25 см;
-
Выразите в квадратных метрах: 50000 см2;
-
Выразите в арах: 300 м2, 4000000см2.
Ф.И. _______________________________________ класс_______
Практическая работа по теме
“Площадь поверхности куба и прямоугольного параллелепипеда”
Вариант 2.
Цель работы:
-
Познакомиться с алгоритмом измерения длины, ширины и высоты куба и прямоугольного параллелепипеда.
-
Научиться вычислять площадь поверхности куба и прямоугольного параллелепипеда.
Оборудование: прямоугольные параллелепипеды (модели, или предметы, имеющие форму прямоугольного параллелепипеда), линейки.
Ход работы.
Работа в парах.
-
И змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
| Длина а см | Ширина b см | Высота c см | Площадь поверхности Sсм2 |
|
|
|
|
|
-
Вычислите площадь полной поверхности прямоугольного параллелепипеда.
S= 2(ab+bc+ac).

Ответ внесите в таблицу.
Индивидуальная работа.
-
Н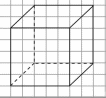 а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки
1 см × 1 см изображен куб. Найдите длину ребра куба. Результат запишите в таблицу.
а
| Длина ребра а см | Площадь одной грани а2 см2 | Количество граней куба | Площадь поверхности куба Sсм2 |
|
|
|
|
|
-
В
а
ычислите площадь одной грани куба. S=а2 .Результат занесите в таблицу. -
Впишите число граней куба в таблицу.
-
В ычислите площадь поверхности куба.
ычислите площадь поверхности куба.
Ответ внесите в таблицу.
Контрольные вопросы.
-
Чем отличается куб от прямоугольного параллелепипеда? Сделайте вывод и запишите его.
-
Что можно сказать про все грани прямоугольного параллелепипеда?Сделайте вывод и запишите его.

Дополнительные задания.
-
Выразите в метрах: 28 м 50 см; 105 м 25 см;
-
Выразите в квадратных метрах: 80000 см2;
-
Выразите в арах: 200 м2, 7000000см2.
Ф.И. _______________________________________ класс_______
Практическая работа по теме
“Площадь поверхности куба и прямоугольного параллелепипеда”
Вариант 3.
Цель работы:
-
Познакомиться с алгоритмом измерения длины, ширины и высоты куба и прямоугольного параллелепипеда.
-
Научиться вычислять площадь поверхности куба и прямоугольного параллелепипеда.
Оборудование: прямоугольные параллелепипеды (модели, или предметы, имеющие форму прямоугольного параллелепипеда), линейки.
Ход работы.
Работа в парах.
-
И змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
| Длина а см | Ширина b см | Высота c см | Площадь поверхности Sсм2 |
|
|
|
|
|
-
Вычислите площадь полной поверхности прямоугольного параллелепипеда.
S= 2(ab+bc+ac).

Ответ внесите в таблицу.
Индивидуальная работа.
-
Н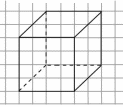 а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки
1 см × 1 см изображен куб. Найдите длину ребра куба. Результат запишите в таблицу.
а
а
| Длина ребра а см | Площадь одной грани а2 см2 | Количество граней куба | Площадь поверхности куба Sсм2 |
|
|
|
|
|
-
Вычислите площадь одной грани куба. S=а2 .Результат занесите в таблицу.
-
Впишите число граней куба в таблицу.
-
В ычислите площадь поверхности куба.
ычислите площадь поверхности куба.
Ответ внесите в таблицу.
Контрольные вопросы.
-
У какого параллелепипеда все грани прямоугольники? Сделайте вывод и запишите его.
-
У какого параллелепипеда все грани квадраты?Сделайте вывод и запишите его.

Дополнительные задания.
-
Выразите в метрах: 93 м 50 см; 509 м 25 см;
-
Выразите в квадратных метрах: 90000 см2;
-
Выразите в арах: 600 м2, 1000000см2.
Ф.И. _______________________________________ класс_______
Практическая работа по теме
“Площадь поверхности куба и прямоугольного параллелепипеда”
Вариант 4.
Цель работы:
-
Познакомиться с алгоритмом измерения длины, ширины и высоты куба и прямоугольного параллелепипеда.
-
Научиться вычислять площадь поверхности куба и прямоугольного параллелепипеда.
Оборудование: прямоугольные параллелепипеды (модели, или предметы, имеющие форму прямоугольного параллелепипеда), линейки.
Ход работы.
Работа в парах.
-
И змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
| Длина а см | Ширина b см | Высота c см | Площадь поверхности Sсм2 |
|
|
|
|
|
-
Вычислите площадь полной поверхности прямоугольного параллелепипеда.
S= 2(ab+bc+ac).

Ответ внесите в таблицу.
И ндивидуальная работа.
ндивидуальная работа.
-
На клетчатой бумаге с размером клетки
1
а
см × 1 см изображен куб. Найдите длину ребра куба. Результат запишите в таблицу.
а
| Длина ребра а см | Площадь одной грани а2 см2 | Количество граней куба | Площадь поверхности куба Sсм2 |
|
|
|
|
|
-
Вычислите площадь одной грани куба. S=а2 .Результат занесите в таблицу.
-
Впишите число граней куба в таблицу.
-
В ычислите площадь поверхности куба.
ычислите площадь поверхности куба.
Ответ внесите в таблицу.
Контрольные вопросы.
-
Чем отличается куб от прямоугольного параллелепипеда? Сделайте вывод и запишите его.
-
Что можно сказать о противоположных гранях параллелепипеда? Сделайте вывод и запишите его.

Дополнительные задания.
-
Выразите в метрах: 29м 50 см;205 м 25 см;
-
Выразите в квадратных метрах: 30000 см2;
-
Выразите в арах: 400 м2, 2000000см2.






 ознакомьтесь с алгоритмомпостроения окружности и изучите ее свойства.
ознакомьтесь с алгоритмомпостроения окружности и изучите ее свойства. равните длину диаметра с длиной радиуса.
равните длину диаметра с длиной радиуса.







 ознакомьтесь с алгоритмомпостроенияугол с помощью транспортира.
ознакомьтесь с алгоритмомпостроенияугол с помощью транспортира.

















 змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба).
змерьте длину, ширину и высоту прямоугольного параллелепипеда (куба). змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.
змерьте длину, ширину и высоту прямоугольного параллелепипеда и заполните таблицу.


 а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки  а клетчатой бумаге с размером клетки
а клетчатой бумаге с размером клетки  ндивидуальная работа.
ндивидуальная работа.





















